2021-2022学年人教版九年级数学下册27.2.1相似三角形的判定同步习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2.1相似三角形的判定同步习题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 733.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 19:04:09 | ||
图片预览


文档简介
《相似三角形的判定》习题
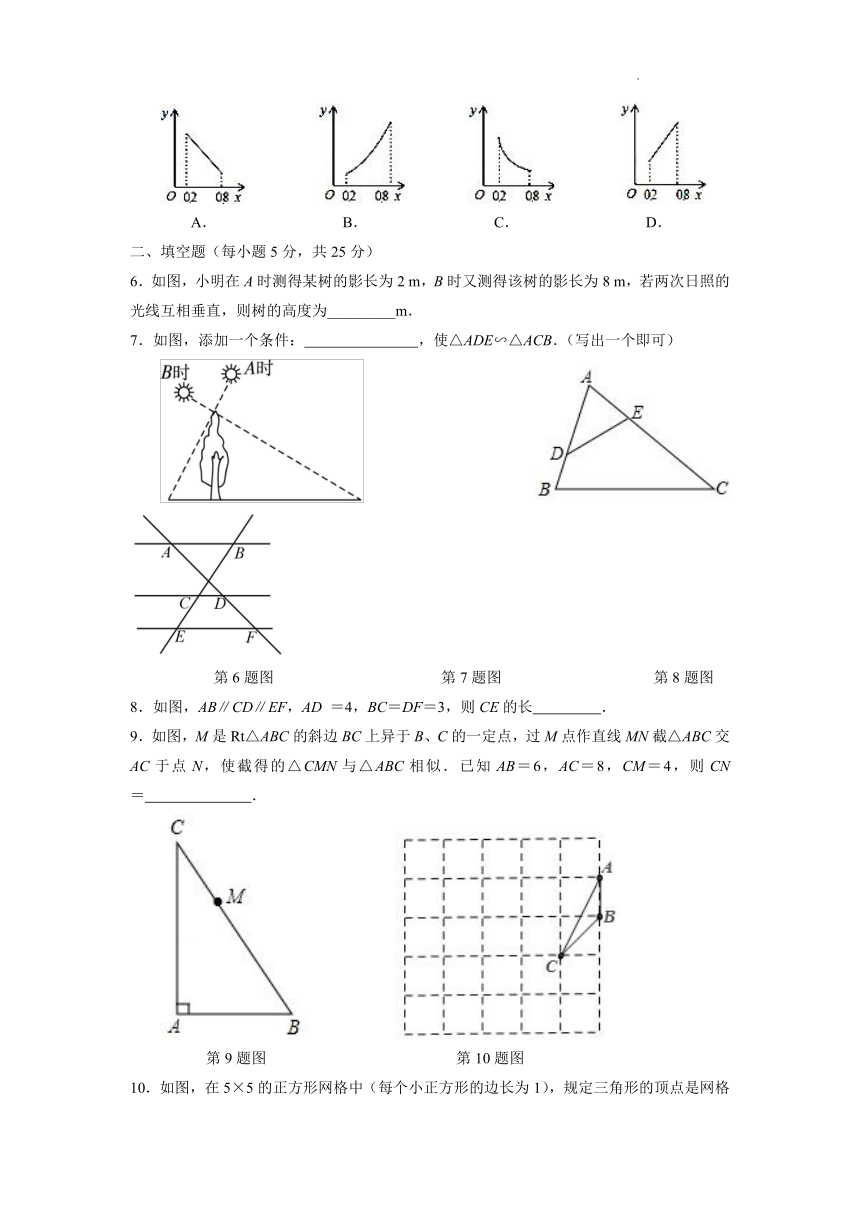
一、选择题(每小题5分,共25分)
1.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD·AB.其中能够单独判定△ABC∽△ACD的条件个数为( )
A.1 B.2 C.3 D.4
第1题图 第3题图
2.下列命题中正确的有( )
①有一个角等于80°的两个等腰三角形相似; ②两边对应成比例的两个等腰三角形相似;③有一个角对应相等的两个等腰三角形相似; ④底边对应相等的两个等腰三角形相似.
A.0个 B.1个 C.2个 D.3个
3.如图,△ABC中,DE∥BC,DE=1,AD=2,DB=3,则BC的长是( )
A. B. C. D.
4.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
5.如图,边长为的正方形中,点在延长线上,连接交于点,(),.则在下面函数图象中,大致能反映与之闻函数关系的是( )
A. B. C. D.
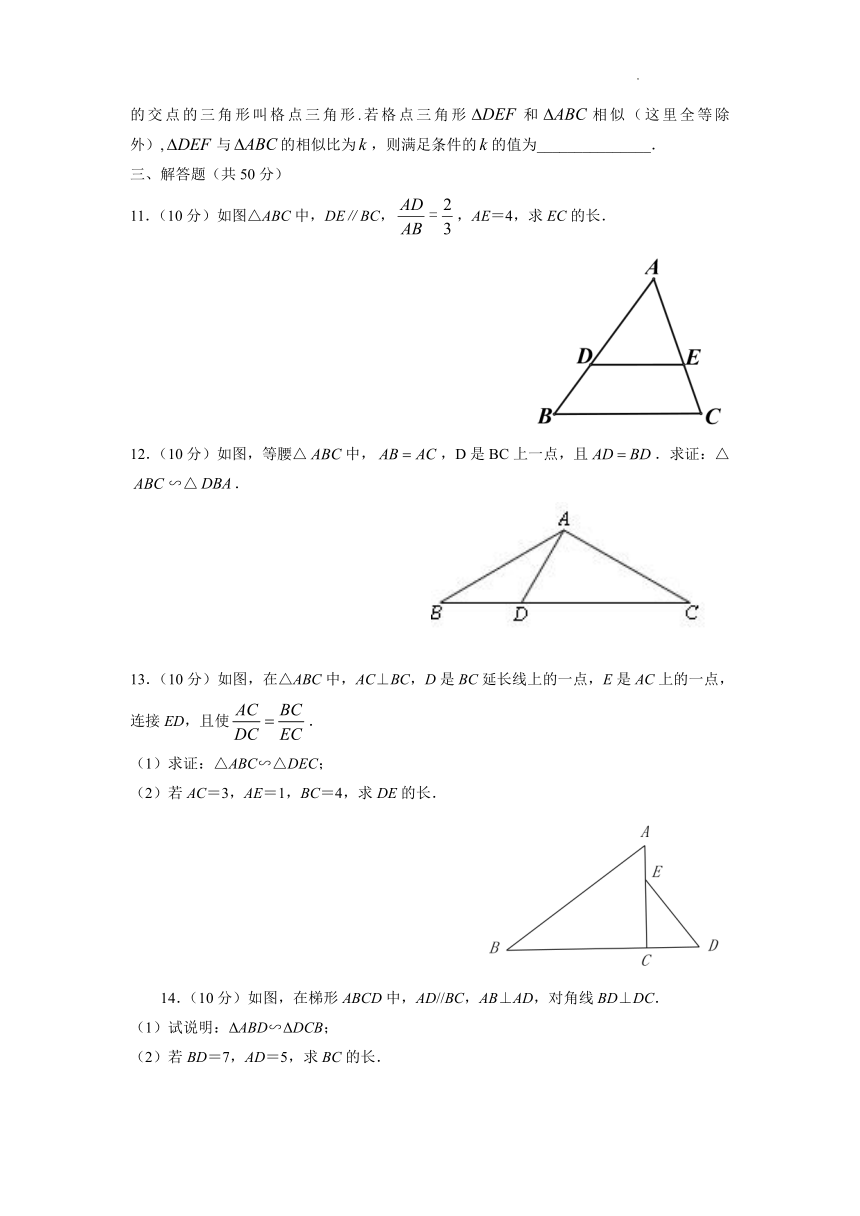
二、填空题(每小题5分,共25分)
6.如图,小明在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则树的高度为_________m.
7.如图,添加一个条件: ,使△ADE∽△ACB.(写出一个即可)
第6题图 第7题图 第8题图
8.如图,AB∥CD∥EF,AD =4,BC=DF=3,则CE的长 .
9.如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线MN截△ABC交AC于点N,使截得的△CMN与△ABC相似.已知AB=6,AC=8,CM=4,则CN= .
第9题图 第10题图
10.如图,在5×5的正方形网格中(每个小正方形的边长为1),规定三角形的顶点是网格的交点的三角形叫格点三角形.若格点三角形和相似(这里全等除外),与的相似比为,则满足条件的的值为_______________.
三、解答题(共50分)
11.(10分)如图△ABC中,DE∥BC,,AE=4,求EC的长.
12.(10分)如图,等腰△中,,D是BC上一点,且.求证:△∽△.
13.(10分)如图,在△ABC中,AC⊥BC,D是BC延长线上的一点,E是AC上的一点,连接ED,且使.
(1)求证:△ABC∽△DEC;
(2)若AC=3,AE=1,BC=4,求DE的长.
14.(10分)如图,在梯形ABCD中,AD//BC,AB⊥AD,对角线BD⊥DC.
(1)试说明:ΔABD∽ΔDCB;
(2)若BD=7,AD=5,求BC的长.
15.(10分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
参考答案
1.C
【解析】有三个.
①∠B=∠ACD,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
②∠ADC=∠ACB,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
③中∠A不是已知的比例线段的夹角,不正确;
④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
故选:C.
2.A
【解析】根据相似三角形的判定对各个选项进行分析,从而得到最后答案:
不正确,由于80°是锐角,可以作等腰三角形的顶角或底角,故不一定相似;
②不正确,两边对应成比例且夹角相等的两三角形相似,等腰三角形的角没说是哪个对应,故不一定相似;
③不正确,由于没说明是顶角还是底角对应,因此不一定相似;
④不正确,底边对应相等,但腰不一定对应相等,角不一定对应相等,故不一定相似;
所以正确的有0个.
故选A
3.C
【解析】根据DE∥BC可以得到△ADE∽△ABC,所以,即,求出BC的值.
4.C.
【解析】 原三角形的边长为:,2,.
A中三角形的边长为:1,,.
B中三角形的边长为:,,3.中三角形的边长为:1,,.有,即相似;
C中三角形的边长为:1,,.
D中三角形的边长为:2,,.
故选C.
5.C
【解析】由图知,∽,所以,因为,所以
.,即().选项中只有C的图像是反比例函数图像,故选C.
6.4
【解析】根据题意,画出示意图,易得:Rt△EDC∽Rt△CDF,且ED=2,FD=8,进而可得;即,代入数据可得,可求得答案DC=4m.
7.答数不唯一,如∠ADE=∠ACB
【解析】相似三角形的判定有三种方法:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.由此可得出可添加的条件.
解:由题意得,∠A=∠A(公共角),
则可添加:∠ADE=∠ACB,利用两角法可判定△ADE∽△ACB.
8.
【解析】有平行线所截线段对应成比例可得:所以CE==.
9.5或
【解析】本题需要分两种情况进行讨论,①、∠CNM=∠A=90°;②∠CMN=∠A=90°,根据这两种情况分别计算CN的长度.
10.
【解析】由图知,格点三角形的三边长为,若要与其相似,且为格点三角形,则边长应为的k倍.当相似比时,三边长为;当相似比k=2 时,三边长为;当相似比时,三边长为;当相似比时,三边长为,此时三角形已占满大正方形,故讨论完毕.
11.2
【解析】首先根据DE∥BC得到△ADE和△ABC相似,求出AC的长度,然后根据CE=AC-AE求出长度.
解:∵DE∥BC
∴△ADE∽△ABC
∴
∵AE=4
∴AC=6
∴EC=AC-AE=6-4=2
12.证明见解析.
【解析】由等边对等角,可得∠B=∠C,∠B=∠DAB,即可求得△ABC∽△DBA.
解:∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠DAB,
∴∠B=∠C=∠DAB,
∴△ABC∽△DBA;
13.(1)证明见解析;(2).
【解析】(1)利用两边成比例且夹角相等,即可判断出△ABC∽△DEC;
(2)由AC=3,AE=1,得出CE=2,根据勾股定理求得AB=5,再利用△ABC∽△DEC得出AB:DE=BC:CE得出结论即可.
解:(1)证明:∵AC⊥BC,
∴∠ACB=∠DCE=90°,
又∵,
∴△ABC∽△DEC.
(2)解:∵AC=3,AE=1,BC=4,
∴CE=2,AB==5,
∵△ABC∽△DEC,
∴,
即,
∴DE=.
14.(1)详见解析;(2)
【解析】
解:
(2)由(1)得
;即:
又∵BD=7,AD=5
∴
15.(1)详见解析;(2)6
【解析】
解:(1)证明:∵平行四边形ABCD,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵平行四边形ABCD,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴,∴DE=12.
在Rt△ADE中,由勾股定理得:AE=6.
一、选择题(每小题5分,共25分)
1.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD·AB.其中能够单独判定△ABC∽△ACD的条件个数为( )
A.1 B.2 C.3 D.4
第1题图 第3题图
2.下列命题中正确的有( )
①有一个角等于80°的两个等腰三角形相似; ②两边对应成比例的两个等腰三角形相似;③有一个角对应相等的两个等腰三角形相似; ④底边对应相等的两个等腰三角形相似.
A.0个 B.1个 C.2个 D.3个
3.如图,△ABC中,DE∥BC,DE=1,AD=2,DB=3,则BC的长是( )
A. B. C. D.
4.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
5.如图,边长为的正方形中,点在延长线上,连接交于点,(),.则在下面函数图象中,大致能反映与之闻函数关系的是( )
A. B. C. D.
二、填空题(每小题5分,共25分)
6.如图,小明在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则树的高度为_________m.
7.如图,添加一个条件: ,使△ADE∽△ACB.(写出一个即可)
第6题图 第7题图 第8题图
8.如图,AB∥CD∥EF,AD =4,BC=DF=3,则CE的长 .
9.如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线MN截△ABC交AC于点N,使截得的△CMN与△ABC相似.已知AB=6,AC=8,CM=4,则CN= .
第9题图 第10题图
10.如图,在5×5的正方形网格中(每个小正方形的边长为1),规定三角形的顶点是网格的交点的三角形叫格点三角形.若格点三角形和相似(这里全等除外),与的相似比为,则满足条件的的值为_______________.
三、解答题(共50分)
11.(10分)如图△ABC中,DE∥BC,,AE=4,求EC的长.
12.(10分)如图,等腰△中,,D是BC上一点,且.求证:△∽△.
13.(10分)如图,在△ABC中,AC⊥BC,D是BC延长线上的一点,E是AC上的一点,连接ED,且使.
(1)求证:△ABC∽△DEC;
(2)若AC=3,AE=1,BC=4,求DE的长.
14.(10分)如图,在梯形ABCD中,AD//BC,AB⊥AD,对角线BD⊥DC.
(1)试说明:ΔABD∽ΔDCB;
(2)若BD=7,AD=5,求BC的长.
15.(10分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
参考答案
1.C
【解析】有三个.
①∠B=∠ACD,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
②∠ADC=∠ACB,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
③中∠A不是已知的比例线段的夹角,不正确;
④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
故选:C.
2.A
【解析】根据相似三角形的判定对各个选项进行分析,从而得到最后答案:
不正确,由于80°是锐角,可以作等腰三角形的顶角或底角,故不一定相似;
②不正确,两边对应成比例且夹角相等的两三角形相似,等腰三角形的角没说是哪个对应,故不一定相似;
③不正确,由于没说明是顶角还是底角对应,因此不一定相似;
④不正确,底边对应相等,但腰不一定对应相等,角不一定对应相等,故不一定相似;
所以正确的有0个.
故选A
3.C
【解析】根据DE∥BC可以得到△ADE∽△ABC,所以,即,求出BC的值.
4.C.
【解析】 原三角形的边长为:,2,.
A中三角形的边长为:1,,.
B中三角形的边长为:,,3.中三角形的边长为:1,,.有,即相似;
C中三角形的边长为:1,,.
D中三角形的边长为:2,,.
故选C.
5.C
【解析】由图知,∽,所以,因为,所以
.,即().选项中只有C的图像是反比例函数图像,故选C.
6.4
【解析】根据题意,画出示意图,易得:Rt△EDC∽Rt△CDF,且ED=2,FD=8,进而可得;即,代入数据可得,可求得答案DC=4m.
7.答数不唯一,如∠ADE=∠ACB
【解析】相似三角形的判定有三种方法:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.由此可得出可添加的条件.
解:由题意得,∠A=∠A(公共角),
则可添加:∠ADE=∠ACB,利用两角法可判定△ADE∽△ACB.
8.
【解析】有平行线所截线段对应成比例可得:所以CE==.
9.5或
【解析】本题需要分两种情况进行讨论,①、∠CNM=∠A=90°;②∠CMN=∠A=90°,根据这两种情况分别计算CN的长度.
10.
【解析】由图知,格点三角形的三边长为,若要与其相似,且为格点三角形,则边长应为的k倍.当相似比时,三边长为;当相似比k=2 时,三边长为;当相似比时,三边长为;当相似比时,三边长为,此时三角形已占满大正方形,故讨论完毕.
11.2
【解析】首先根据DE∥BC得到△ADE和△ABC相似,求出AC的长度,然后根据CE=AC-AE求出长度.
解:∵DE∥BC
∴△ADE∽△ABC
∴
∵AE=4
∴AC=6
∴EC=AC-AE=6-4=2
12.证明见解析.
【解析】由等边对等角,可得∠B=∠C,∠B=∠DAB,即可求得△ABC∽△DBA.
解:∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠DAB,
∴∠B=∠C=∠DAB,
∴△ABC∽△DBA;
13.(1)证明见解析;(2).
【解析】(1)利用两边成比例且夹角相等,即可判断出△ABC∽△DEC;
(2)由AC=3,AE=1,得出CE=2,根据勾股定理求得AB=5,再利用△ABC∽△DEC得出AB:DE=BC:CE得出结论即可.
解:(1)证明:∵AC⊥BC,
∴∠ACB=∠DCE=90°,
又∵,
∴△ABC∽△DEC.
(2)解:∵AC=3,AE=1,BC=4,
∴CE=2,AB==5,
∵△ABC∽△DEC,
∴,
即,
∴DE=.
14.(1)详见解析;(2)
【解析】
解:
(2)由(1)得
;即:
又∵BD=7,AD=5
∴
15.(1)详见解析;(2)6
【解析】
解:(1)证明:∵平行四边形ABCD,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵平行四边形ABCD,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴,∴DE=12.
在Rt△ADE中,由勾股定理得:AE=6.
