2022年北师大版七年级数学下册 第五章生活中的轴对称 最新强化训练课时练习试卷(word版 含解析)
文档属性
| 名称 | 2022年北师大版七年级数学下册 第五章生活中的轴对称 最新强化训练课时练习试卷(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 404.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 14:10:05 | ||
图片预览



文档简介
七年级数学下册第五章生活中的轴对称课时练习
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定正确的是( )
A.AC=A′C′ B.BO=B′O C.AA′⊥MN D.ABB′C′
2、如图,正方形网格中, A,B两点均在直线a上方,要在直线a上求一点P,使PA+PB的值最小,则点P应选在( )
A.C点 B.D点 C.E点 D.F点
3、如图,直线、相交于点,为这两条直线外一点,连接.点关于直线、的对称点分别是点、.若,则点、之间的距离可能是( )
A. B. C. D.
4、下列四个标志中,是轴对称图形的是( )
A. B.
C. D.
5、以下是四个我国杰出企业代表的标志,其中是轴对称图形的是( )
A. B. C. D.
6、下列图标中是轴对称图形的是( )
A. B.
C. D.
7、如图,AD,BE,CF依次是ABC的高、中线和角平分线,下列表达式中错误的是( )
A.AE=CE B.∠ADC=90° C.∠CAD=∠CBE D.∠ACB=2∠ACF
8、下列交通标志中,是轴对称图形的是( )
A. B.
C. D.
9、下面是四家医院标志的图案部分,其中是轴对称图形的是( )
A. B.
C. D.
10、如图,点D是∠FAB内的定点且AD=2,若点C、E分别是射线AF、AB上异于点A的动点,且△CDE周长的最小值是2时,∠FAB的度数是( )
A.30° B.45° C.60° D.90°
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、下列图形中,一定是轴对称图形的有______________(填序号).
(1)线段;(2)三角形;(3)圆;(4)正方形;(5)梯形
2、汉字中、日、田等都可看作是轴对称图形,请你再写出一个这样的汉字:______.
3、如图,△ABD和△ACD关于直线AD对称,若S△ABC=12,则图中阴影部分面积为 ___.
4、如图,点关于、的对称点分别是,,线段分别交、于、,cm,则的周长为________ cm.
5、图中与标号“1”的三角形成轴对称的三角形的个数为________.
三、解答题(5小题,每小题10分,共计50分)
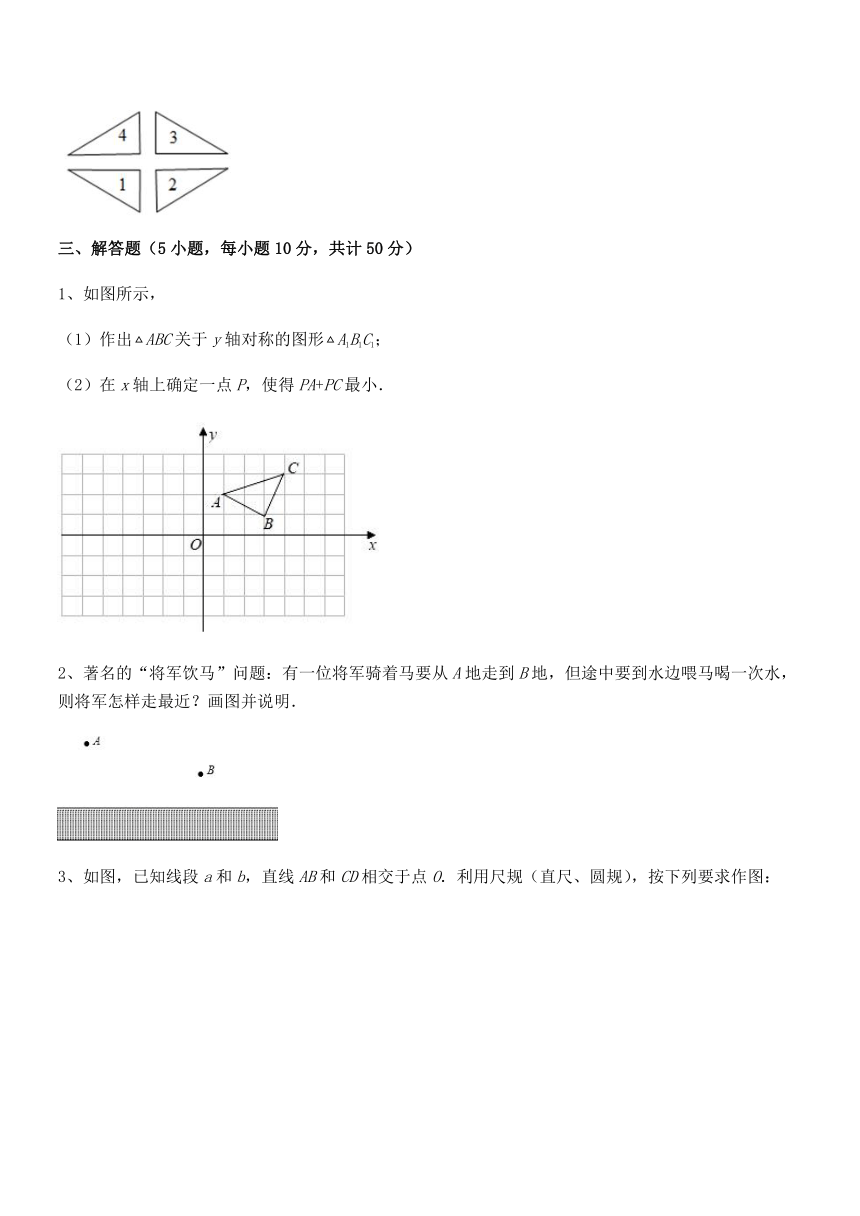
1、如图所示,
(1)作出ABC关于y轴对称的图形A1B1C1;
(2)在x轴上确定一点P,使得PA+PC最小.
2、著名的“将军饮马”问题:有一位将军骑着马要从A地走到B地,但途中要到水边喂马喝一次水,则将军怎样走最近?画图并说明.
3、如图,已知线段a和b,直线AB和CD相交于点O.利用尺规(直尺、圆规),按下列要求作图:
(1)在射线OA,OB,OC上作线段OA',OB',OC',使它们分别与线段a相等;
(2)在射线OD上作线段OD',使OD'与线段b相等;
(3)连接A'C',C'B',B'D',D'A';
(4)你得到了一个怎样的图形?
4、如图,在△ABC中,AD⊥BE,∠DAC=10°,AE是∠BAC的外角∠MAC的平分线,BF平分∠ABC交AE于点F,求∠AFB的度数.
5、如图,把下列图形补成关于直线l对称的图形.
-参考答案-
一、单选题
1、D
【分析】
根据轴对称的性质解答.
【详解】
解:∵△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,
∴AC=A′C′,BO=B′O,AA′⊥MN,但ABB′C′不正确,
故选:D.
【点睛】
此题考查了轴对称的性质:轴对称两个图形的对应边相等,对应角相等,熟记性质是解题的关键.
2、C
【分析】
取A点关于直线a的对称点G,连接BG与直线a交于点E,点E即为所求.
【详解】
解:如图所示,取A点关于直线a的对称点G,连接BG与直线a交于点E,点E即为所求,
故选C.
【点睛】
本题主要考查了轴对称最短路径问题,解题的关键在于能够熟练掌握轴对称最短路径的相关知识.
3、B
【分析】
由对称得OP1=OP=3.5,OP=OP2=3.5,再根据三角形任意两边之和大于第三边,即可得出结果.
【详解】
连接,,,如图:
点关于直线,的对称点分别是点,,
,,
,
,
故选:.
【点睛】
本题考查线轴对称的性质以及三角形三边关系,解本题的关键熟练掌握对称性和三角形边长的关系.
4、D
【分析】
利用轴对称图形的定义进行解答即可.
【详解】
解:A、不是轴对称图形,故此选项不合题意;
B、不是轴对称图形,故此选项不符合题意;
C、不是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项符合题意;
故选:D.
【点睛】
此题主要考查了轴对称图形,关键是掌握如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
5、B
【详解】
解:A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意;
故选:B
【点睛】
本题主要考查了轴对称图形的定义,熟练掌握若一个图形沿着一条直线折叠后两部分能完全重合,这样的图形就叫做轴对称图形,这条直线叫做对称轴是解题的关键.
6、B
【详解】
解:选项A中的图形不是轴对称图形,故A不符合题意;
选项B中的图形是轴对称图形,故B符合题意;
选项C中的图形不是轴对称图形,故C不符合题意;
选项D中的图形不是轴对称图形,故D不符合题意;
故选B
【点睛】
本题考查的是轴对称图形的识别,轴对称图形的概念:把一个图形沿某条直线对折,对折后直线两旁的部分能够完全重合;掌握“轴对称图形的概念”是解本题的关键.
7、C
【分析】
根据三角形的高、中线和角平分线的定义(1)三角形的角平分线定义:三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点和交点的线段叫做三角形的角平分线;(2)三角形的中线定义:在三角形中,连接一个顶点和它所对边的中点的连线段叫做三角形的中线;(3)三角形的高定义:从三角形一个顶点向它的对边(或对边所在的直线)作垂线,顶点和垂足间的线段叫做三角形的高线,简称为高.求解即可.
【详解】
解:A、BE是△ABC的中线,所以AE=CE,故本表达式正确;
B、AD是△ABC的高,所以∠ADC=90,故本表达式正确;
C、由三角形的高、中线和角平分线的定义无法得出∠CAD=∠CBE,故本表达式错误;
D、CF是△ABC的角平分线,所以∠ACB=2∠ACF,故本表达式正确.
故选:C.
【点睛】
本题考查了三角形的高、中线和角平分线的定义,是基础题,熟记定义是解题的关键.
8、C
【分析】
根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,进行判断即可.
【详解】
解:解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、是轴对称图形,故本选项正确;
D、不是轴对称图形,故本选项错误;
故选C.
【点睛】
本题考查了轴对称图形的知识,属于基础题,掌握轴对称的定义是关键.
9、A
【分析】
根据轴对称图形的概念逐项判断解答即可.
【详解】
.是轴对称图形,选项正确;
.不是轴对称图形,选项错误;
.不是轴对称图形,选项错误;
.不是轴对称图形,选项错误;
故选:
【点睛】
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后能重合.
10、A
【分析】
作D点分别关于AF、AB的对称点G、H,连接GH分别交AF、AB于C′、E′,利用轴对称的性质得AG=AD=AH=2,利用两点之间线段最短判断此时△CDE周长最小为DC′+DE′+C′E′=GH=2,可得△AGH是等边三角形,进而可得∠FAB的度数.
【详解】
解:如图,作D点分别关于AF、AB的对称点G、H,连接GH分别交AF、AB于C′、E′,连接DC′,DE′,
此时△CDE周长最小为DC′+DE′+C′E′=GH=2,
根据轴对称的性质,得AG=AD=AH=2,∠DAF=∠GAF,∠DAB=∠HAB,
∴AG=AH=GH=2,
∴△AGH是等边三角形,
∴∠GAH=60°,
∴∠FAB=∠GAH=30°,
故选:A.
【点睛】
本题考查了轴对称-最短路线问题:熟练掌握轴对称的性质,会利用两点之间线段最短解决路径最短问题.
二、填空题
1、(1)(3)(4)
【分析】
如果一个图形沿着一条直线对折后,直线两旁的部分完全重合,这样的图形叫做轴对称图形,依据定义即可作出判断.
【详解】
解:线段的对称轴是其垂直平分线,圆的对称轴是其直径所在的直线,正方形的对称轴是其对角线所在直线和对边中点的连线,
(1)(3)(4)是轴对称图形,
只有等腰三角形和等腰梯形是轴对称图形,(2)(5)不一定是轴对称图形,
故一定是轴对称图形的有(1)(3)(4).
故答案为:(1)(3)(4).
【点睛】
本题主要考查了轴对称图形的定义,解题的关键是正确确定轴对称图形的对称轴.
2、一(答案不唯一)
【分析】
如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答即可.
【详解】
解:由轴对称图形的定义可得:一、二、三、甲、出、本、王、平都是轴对称图形.
故答案为:一(答案不唯一).
【点睛】
此题主要考查了轴对称图形,掌握轴对称图形的意义,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合.
3、6
【分析】
根据轴对称的性质可得,,由此即可得出答案.
【详解】
解:和关于直线对称,,
,,
则图中阴影部分面积为,
故答案为:6.
【点睛】
本题考查了轴对称的性质,熟练掌握轴对称的性质是解题关键.
4、8
【分析】
首先根据点P关于OA、OB的对称点分别是P1,P2,可得PD=P1D,PC=P2C;然后根据P1P2=8cm,可得P1D+DC+P2C=8cm,所以PD+DC+PC=8cm,即△PCD的周长为8cm,据此解答即可.
【详解】
解:∵点P关于OA、OB的对称点分别是P1,P2,
∴PD=P1D,PC=P2C;
∵P1P2=8(cm),
∴P1D+DC+P2C=8(cm),
∴PD+DC+PC=8(cm),
即△PCD的周长为8cm.
故答案为:8.
【点睛】
本题考查了轴对称的性质的应用,要熟练掌握,解题的关键是判断出:PD=P1D,PC=P2C.此题还考查了三角形的周长的含义以及求法的应用,要熟练掌握.
5、2个
【分析】
根据轴对称图形的定义(如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形)即可得.
【详解】
解:图中与标号“1”的三角形成轴对称的三角形是标号“2”和“4”,共有2个,
故答案为:2个.
【点睛】
本题考查了轴对称图形,熟记定义是解题关键.
三、解答题
1、(1)见解析;(2)见解析
【分析】
(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可得;
(2)作点C关于x轴的对称点C′,再连接AC′,与x轴的交点即为所求.
【详解】
解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,点P即为所求.
【点睛】
本题考查轴对称的综合应用,熟练掌握轴对称图形的性质及“两点之间线段最短”的基本事实是解题关键.
2、见解析
【分析】
根据轴对称的性质作出B点与河面的对称点B′,连接AB′,AB′与河面的交点C即为所求.
【详解】
解:作B点与河面的对称点B′,连接AB′,可得到马喝水的地方C,
如图所示,
由对称的性质可知AB′=AC+BC,
根据两点之间线段最短的性质可知,C点即为所求.
【点睛】
本题考查的是最短路线问题,解答此题的关键是熟知两点之间线段最短.
3、(1)见解析;(2)见解析;(3)见解析;(4)轴对称图形
【分析】
(1)以为圆心,以线段的长为半径画圆,交OA,OB,OC上于点、、,即可;
(2)以为圆心,以线段的长为半径画圆,交OD上于点,即可;
(3)连接对应线段即可;
(4)根据图形的性质,求解即可.
【详解】
解:(1)以为圆心,以线段的长为半径画圆,交OA,OB,OC上于点、、,如下图:
(2)以为圆心,以线段的长为半径画圆,交OD上于点,如下图:
(3)连接、、、,如下图:
(4)观察图形可得,得到的图形为轴对称图形.
【点睛】
此题考查了尺规作图,作线段,涉及了轴对称图形的识别,解题的关键是按照题意,正确作出图形.
4、∠AFB=40°.
【分析】
由题意易得∠ADC=90°,∠ACB=80°,然后可得,进而根据三角形外角的性质可求解.
【详解】
解:∵AD⊥BE,
∴∠ADC=90°,
∵∠DAC=10°,
∴∠ACB=90°﹣∠DAC=90°﹣10°=80°,
∵AE是∠MAC的平分线,BF平分∠ABC,
∴,
又∵∠MAE=∠ABF+∠AFB,∠MAC=∠ABC+∠ACB,
∴∠AFB=∠MAE﹣∠ABF=.
【点睛】
本题主要考查三角形外角的性质及角平分线的定义,熟练掌握三角形外角的性质及角平分线的定义是解题的关键.
5、见解析
【分析】
根据轴对称图形的性质,先找出各关键点关于直线l的对称点,再顺次连接即可.
【详解】
解:关于直线l对称的图形如图所示.
【点睛】
本题考查作图-轴对称变换,解题的关键是掌握轴对称变换的性质,几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定正确的是( )
A.AC=A′C′ B.BO=B′O C.AA′⊥MN D.ABB′C′
2、如图,正方形网格中, A,B两点均在直线a上方,要在直线a上求一点P,使PA+PB的值最小,则点P应选在( )
A.C点 B.D点 C.E点 D.F点
3、如图,直线、相交于点,为这两条直线外一点,连接.点关于直线、的对称点分别是点、.若,则点、之间的距离可能是( )
A. B. C. D.
4、下列四个标志中,是轴对称图形的是( )
A. B.
C. D.
5、以下是四个我国杰出企业代表的标志,其中是轴对称图形的是( )
A. B. C. D.
6、下列图标中是轴对称图形的是( )
A. B.
C. D.
7、如图,AD,BE,CF依次是ABC的高、中线和角平分线,下列表达式中错误的是( )
A.AE=CE B.∠ADC=90° C.∠CAD=∠CBE D.∠ACB=2∠ACF
8、下列交通标志中,是轴对称图形的是( )
A. B.
C. D.
9、下面是四家医院标志的图案部分,其中是轴对称图形的是( )
A. B.
C. D.
10、如图,点D是∠FAB内的定点且AD=2,若点C、E分别是射线AF、AB上异于点A的动点,且△CDE周长的最小值是2时,∠FAB的度数是( )
A.30° B.45° C.60° D.90°
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、下列图形中,一定是轴对称图形的有______________(填序号).
(1)线段;(2)三角形;(3)圆;(4)正方形;(5)梯形
2、汉字中、日、田等都可看作是轴对称图形,请你再写出一个这样的汉字:______.
3、如图,△ABD和△ACD关于直线AD对称,若S△ABC=12,则图中阴影部分面积为 ___.
4、如图,点关于、的对称点分别是,,线段分别交、于、,cm,则的周长为________ cm.
5、图中与标号“1”的三角形成轴对称的三角形的个数为________.
三、解答题(5小题,每小题10分,共计50分)
1、如图所示,
(1)作出ABC关于y轴对称的图形A1B1C1;
(2)在x轴上确定一点P,使得PA+PC最小.
2、著名的“将军饮马”问题:有一位将军骑着马要从A地走到B地,但途中要到水边喂马喝一次水,则将军怎样走最近?画图并说明.
3、如图,已知线段a和b,直线AB和CD相交于点O.利用尺规(直尺、圆规),按下列要求作图:
(1)在射线OA,OB,OC上作线段OA',OB',OC',使它们分别与线段a相等;
(2)在射线OD上作线段OD',使OD'与线段b相等;
(3)连接A'C',C'B',B'D',D'A';
(4)你得到了一个怎样的图形?
4、如图,在△ABC中,AD⊥BE,∠DAC=10°,AE是∠BAC的外角∠MAC的平分线,BF平分∠ABC交AE于点F,求∠AFB的度数.
5、如图,把下列图形补成关于直线l对称的图形.
-参考答案-
一、单选题
1、D
【分析】
根据轴对称的性质解答.
【详解】
解:∵△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,
∴AC=A′C′,BO=B′O,AA′⊥MN,但ABB′C′不正确,
故选:D.
【点睛】
此题考查了轴对称的性质:轴对称两个图形的对应边相等,对应角相等,熟记性质是解题的关键.
2、C
【分析】
取A点关于直线a的对称点G,连接BG与直线a交于点E,点E即为所求.
【详解】
解:如图所示,取A点关于直线a的对称点G,连接BG与直线a交于点E,点E即为所求,
故选C.
【点睛】
本题主要考查了轴对称最短路径问题,解题的关键在于能够熟练掌握轴对称最短路径的相关知识.
3、B
【分析】
由对称得OP1=OP=3.5,OP=OP2=3.5,再根据三角形任意两边之和大于第三边,即可得出结果.
【详解】
连接,,,如图:
点关于直线,的对称点分别是点,,
,,
,
,
故选:.
【点睛】
本题考查线轴对称的性质以及三角形三边关系,解本题的关键熟练掌握对称性和三角形边长的关系.
4、D
【分析】
利用轴对称图形的定义进行解答即可.
【详解】
解:A、不是轴对称图形,故此选项不合题意;
B、不是轴对称图形,故此选项不符合题意;
C、不是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项符合题意;
故选:D.
【点睛】
此题主要考查了轴对称图形,关键是掌握如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
5、B
【详解】
解:A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意;
故选:B
【点睛】
本题主要考查了轴对称图形的定义,熟练掌握若一个图形沿着一条直线折叠后两部分能完全重合,这样的图形就叫做轴对称图形,这条直线叫做对称轴是解题的关键.
6、B
【详解】
解:选项A中的图形不是轴对称图形,故A不符合题意;
选项B中的图形是轴对称图形,故B符合题意;
选项C中的图形不是轴对称图形,故C不符合题意;
选项D中的图形不是轴对称图形,故D不符合题意;
故选B
【点睛】
本题考查的是轴对称图形的识别,轴对称图形的概念:把一个图形沿某条直线对折,对折后直线两旁的部分能够完全重合;掌握“轴对称图形的概念”是解本题的关键.
7、C
【分析】
根据三角形的高、中线和角平分线的定义(1)三角形的角平分线定义:三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点和交点的线段叫做三角形的角平分线;(2)三角形的中线定义:在三角形中,连接一个顶点和它所对边的中点的连线段叫做三角形的中线;(3)三角形的高定义:从三角形一个顶点向它的对边(或对边所在的直线)作垂线,顶点和垂足间的线段叫做三角形的高线,简称为高.求解即可.
【详解】
解:A、BE是△ABC的中线,所以AE=CE,故本表达式正确;
B、AD是△ABC的高,所以∠ADC=90,故本表达式正确;
C、由三角形的高、中线和角平分线的定义无法得出∠CAD=∠CBE,故本表达式错误;
D、CF是△ABC的角平分线,所以∠ACB=2∠ACF,故本表达式正确.
故选:C.
【点睛】
本题考查了三角形的高、中线和角平分线的定义,是基础题,熟记定义是解题的关键.
8、C
【分析】
根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,进行判断即可.
【详解】
解:解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、是轴对称图形,故本选项正确;
D、不是轴对称图形,故本选项错误;
故选C.
【点睛】
本题考查了轴对称图形的知识,属于基础题,掌握轴对称的定义是关键.
9、A
【分析】
根据轴对称图形的概念逐项判断解答即可.
【详解】
.是轴对称图形,选项正确;
.不是轴对称图形,选项错误;
.不是轴对称图形,选项错误;
.不是轴对称图形,选项错误;
故选:
【点睛】
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后能重合.
10、A
【分析】
作D点分别关于AF、AB的对称点G、H,连接GH分别交AF、AB于C′、E′,利用轴对称的性质得AG=AD=AH=2,利用两点之间线段最短判断此时△CDE周长最小为DC′+DE′+C′E′=GH=2,可得△AGH是等边三角形,进而可得∠FAB的度数.
【详解】
解:如图,作D点分别关于AF、AB的对称点G、H,连接GH分别交AF、AB于C′、E′,连接DC′,DE′,
此时△CDE周长最小为DC′+DE′+C′E′=GH=2,
根据轴对称的性质,得AG=AD=AH=2,∠DAF=∠GAF,∠DAB=∠HAB,
∴AG=AH=GH=2,
∴△AGH是等边三角形,
∴∠GAH=60°,
∴∠FAB=∠GAH=30°,
故选:A.
【点睛】
本题考查了轴对称-最短路线问题:熟练掌握轴对称的性质,会利用两点之间线段最短解决路径最短问题.
二、填空题
1、(1)(3)(4)
【分析】
如果一个图形沿着一条直线对折后,直线两旁的部分完全重合,这样的图形叫做轴对称图形,依据定义即可作出判断.
【详解】
解:线段的对称轴是其垂直平分线,圆的对称轴是其直径所在的直线,正方形的对称轴是其对角线所在直线和对边中点的连线,
(1)(3)(4)是轴对称图形,
只有等腰三角形和等腰梯形是轴对称图形,(2)(5)不一定是轴对称图形,
故一定是轴对称图形的有(1)(3)(4).
故答案为:(1)(3)(4).
【点睛】
本题主要考查了轴对称图形的定义,解题的关键是正确确定轴对称图形的对称轴.
2、一(答案不唯一)
【分析】
如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答即可.
【详解】
解:由轴对称图形的定义可得:一、二、三、甲、出、本、王、平都是轴对称图形.
故答案为:一(答案不唯一).
【点睛】
此题主要考查了轴对称图形,掌握轴对称图形的意义,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合.
3、6
【分析】
根据轴对称的性质可得,,由此即可得出答案.
【详解】
解:和关于直线对称,,
,,
则图中阴影部分面积为,
故答案为:6.
【点睛】
本题考查了轴对称的性质,熟练掌握轴对称的性质是解题关键.
4、8
【分析】
首先根据点P关于OA、OB的对称点分别是P1,P2,可得PD=P1D,PC=P2C;然后根据P1P2=8cm,可得P1D+DC+P2C=8cm,所以PD+DC+PC=8cm,即△PCD的周长为8cm,据此解答即可.
【详解】
解:∵点P关于OA、OB的对称点分别是P1,P2,
∴PD=P1D,PC=P2C;
∵P1P2=8(cm),
∴P1D+DC+P2C=8(cm),
∴PD+DC+PC=8(cm),
即△PCD的周长为8cm.
故答案为:8.
【点睛】
本题考查了轴对称的性质的应用,要熟练掌握,解题的关键是判断出:PD=P1D,PC=P2C.此题还考查了三角形的周长的含义以及求法的应用,要熟练掌握.
5、2个
【分析】
根据轴对称图形的定义(如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形)即可得.
【详解】
解:图中与标号“1”的三角形成轴对称的三角形是标号“2”和“4”,共有2个,
故答案为:2个.
【点睛】
本题考查了轴对称图形,熟记定义是解题关键.
三、解答题
1、(1)见解析;(2)见解析
【分析】
(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可得;
(2)作点C关于x轴的对称点C′,再连接AC′,与x轴的交点即为所求.
【详解】
解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,点P即为所求.
【点睛】
本题考查轴对称的综合应用,熟练掌握轴对称图形的性质及“两点之间线段最短”的基本事实是解题关键.
2、见解析
【分析】
根据轴对称的性质作出B点与河面的对称点B′,连接AB′,AB′与河面的交点C即为所求.
【详解】
解:作B点与河面的对称点B′,连接AB′,可得到马喝水的地方C,
如图所示,
由对称的性质可知AB′=AC+BC,
根据两点之间线段最短的性质可知,C点即为所求.
【点睛】
本题考查的是最短路线问题,解答此题的关键是熟知两点之间线段最短.
3、(1)见解析;(2)见解析;(3)见解析;(4)轴对称图形
【分析】
(1)以为圆心,以线段的长为半径画圆,交OA,OB,OC上于点、、,即可;
(2)以为圆心,以线段的长为半径画圆,交OD上于点,即可;
(3)连接对应线段即可;
(4)根据图形的性质,求解即可.
【详解】
解:(1)以为圆心,以线段的长为半径画圆,交OA,OB,OC上于点、、,如下图:
(2)以为圆心,以线段的长为半径画圆,交OD上于点,如下图:
(3)连接、、、,如下图:
(4)观察图形可得,得到的图形为轴对称图形.
【点睛】
此题考查了尺规作图,作线段,涉及了轴对称图形的识别,解题的关键是按照题意,正确作出图形.
4、∠AFB=40°.
【分析】
由题意易得∠ADC=90°,∠ACB=80°,然后可得,进而根据三角形外角的性质可求解.
【详解】
解:∵AD⊥BE,
∴∠ADC=90°,
∵∠DAC=10°,
∴∠ACB=90°﹣∠DAC=90°﹣10°=80°,
∵AE是∠MAC的平分线,BF平分∠ABC,
∴,
又∵∠MAE=∠ABF+∠AFB,∠MAC=∠ABC+∠ACB,
∴∠AFB=∠MAE﹣∠ABF=.
【点睛】
本题主要考查三角形外角的性质及角平分线的定义,熟练掌握三角形外角的性质及角平分线的定义是解题的关键.
5、见解析
【分析】
根据轴对称图形的性质,先找出各关键点关于直线l的对称点,再顺次连接即可.
【详解】
解:关于直线l对称的图形如图所示.
【点睛】
本题考查作图-轴对称变换,解题的关键是掌握轴对称变换的性质,几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
