2021-2022学年人教版数学九年级下册26.1.2反比例函数的图像和性质同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册26.1.2反比例函数的图像和性质同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 437.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 21:16:30 | ||
图片预览



文档简介
反比例函数的图像和性质
一、单选题
1.反比例函数y=﹣的图象在第( )象限.
A.一、三象限 B.二、四象限 C.一、二象限 D.二、三象限
2.如果反比例函数y=的图象经过点(3,﹣4),那么k是( )
A.7 B.10 C.12 D.﹣12
3.若反比例函数的图象分布在第二、四象限,则k的取值范围是( )
A.k<2 B.k>2 C.k>1 D.k<1
4.已知反比例函数,当|y|≥3时,x的取值范围是( )
A.x≥2或x≤﹣2 B.﹣2≤x≤2
C.0<x≤2或x≤﹣2 D.﹣2≤x<0或0<x≤2
5.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
6.如果反比例函数(a是常数)的图象所在的每一个象限内,y随x增大而减小,那么a的取值范围是( )
A.a<0 B.a>0 C.a<2 D.a>2
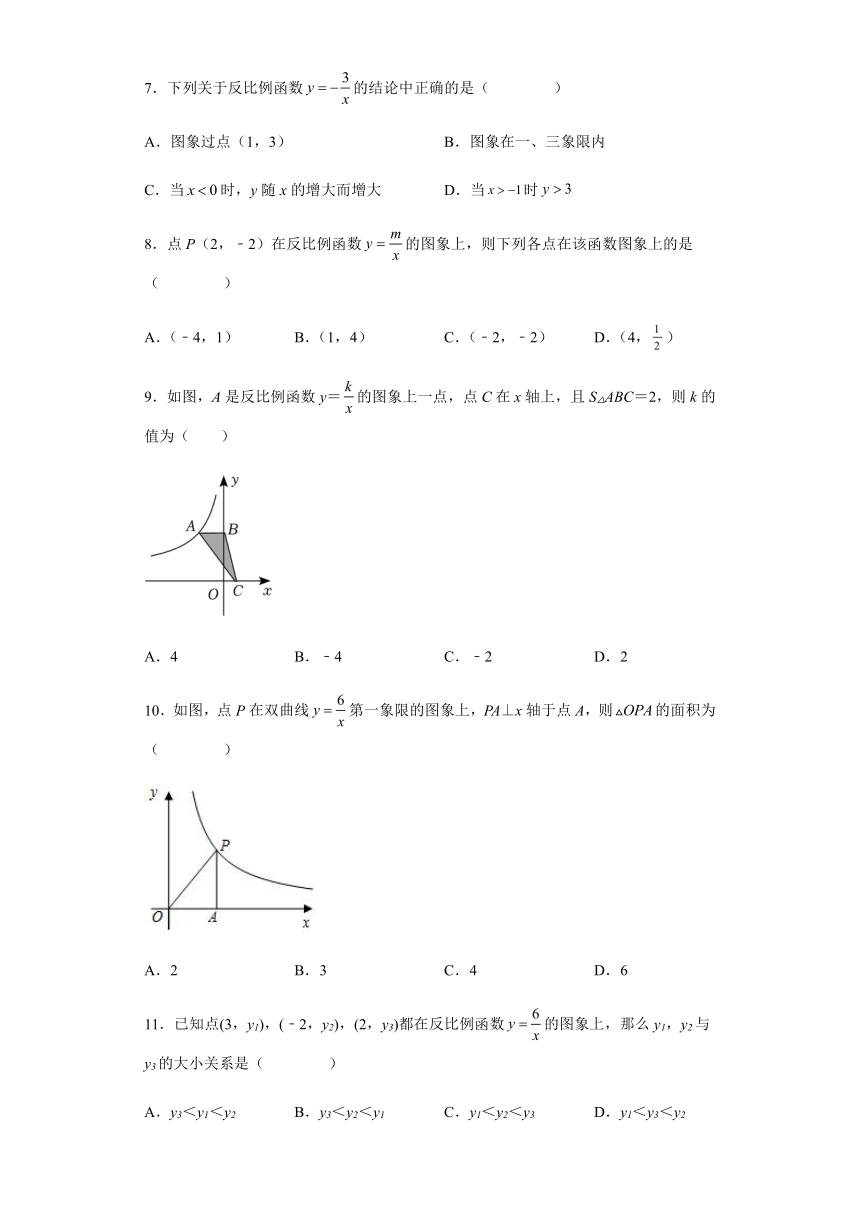
7.下列关于反比例函数的结论中正确的是( )
A.图象过点(1,3) B.图象在一、三象限内
C.当时,y随x的增大而增大 D.当时
8.点P(2,﹣2)在反比例函数的图象上,则下列各点在该函数图象上的是( )
A.(﹣4,1) B.(1,4) C.(﹣2,﹣2) D.(4,)
9.如图,A是反比例函数y=的图象上一点,点C在x轴上,且S△ABC=2,则k的值为( )
A.4 B.﹣4 C.﹣2 D.2
10.如图,点P在双曲线第一象限的图象上,PA⊥x轴于点A,则的面积为( )
A.2 B.3 C.4 D.6
11.已知点(3,y1),(﹣2,y2),(2,y3)都在反比例函数的图象上,那么y1,y2与y3的大小关系是( )
A.y3<y1<y2 B.y3<y2<y1 C.y1<y2<y3 D.y1<y3<y2
12.一次函数与反比例函数上的图象在同一直角坐标系下的大致图象如图所示,则、b的取值范围是( )
A., B., C., D.,
二、填空题
13.已知同一象限内的两点A(3,n),B(n﹣4,n+3)均在反比例函数y=的图象上,则该反比例函数关系式为_____.
14.若点A(﹣2,y1)、B(﹣1,y2)在反比例函数y=图象上,则y1、y2大小关系是_______.
15.如在平面直角坐标系中,等腰直角△ABO如图放置,直角项点A在反比例函数的图形上,其中AB=AO,B(-2,0),则k=___.
16.如图所示,点是双曲线在第二象限的分支上的任意一点,点、、分别是点关于轴、原点、轴的对称点,则四边形的面积是__.
三、解答题
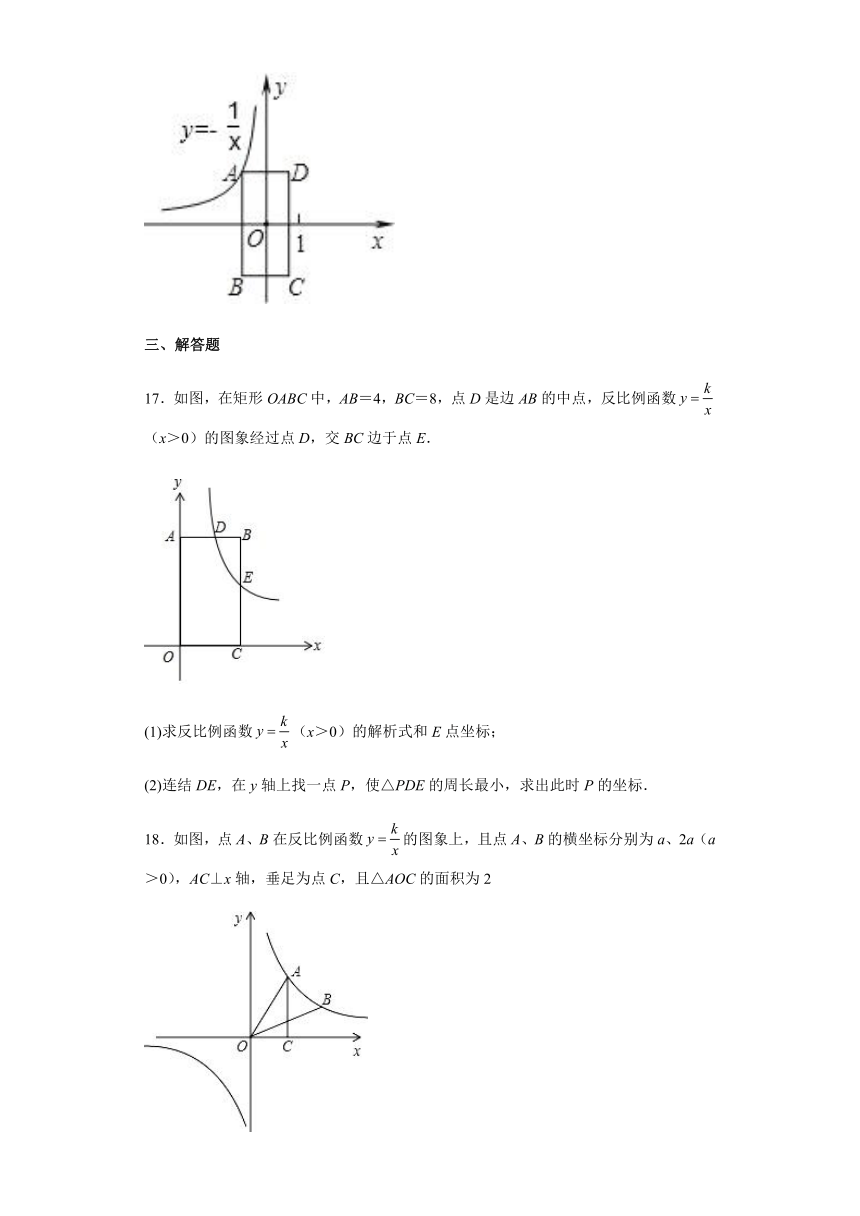
17.如图,在矩形OABC中,AB=4,BC=8,点D是边AB的中点,反比例函数(x>0)的图象经过点D,交BC边于点E.
(1)求反比例函数(x>0)的解析式和E点坐标;
(2)连结DE,在y轴上找一点P,使△PDE的周长最小,求出此时P的坐标.
18.如图,点A、B在反比例函数的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为点C,且△AOC的面积为2
(1)求该反比例函数的解析式;
(2)若点(﹣a,y1),(﹣2a,y2)在该反比例函数的图象上,试比较y1与y2的大小;
(3)求△AOB的面积.
19.如图,一次函数(k为常数,)与反比例函数(m为常数,)的图象交于点和,与y轴交于点M.
(1)求一次函数与反比例函数的表达式;
(2)连接OA、OB,求△AOB的面积,
20.直线与反比例函数的图象分别交于点A(m,4)和点B(8,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当时,直接写出的解集;
(3)若点P是x轴上一动点,当△ADP的面积是6时,求出P点的坐标.
试卷第1页,共3页
参考答案:
1.B
解:∵反比例函数y=-中k=-1<0,
∴图象位于二、四象限,
故选:B.
2.D
解:∵反比例函数y=的图象经过点(3,﹣4),
∴-4=,
解得k=-12.
故选D.
3.B
解:∵反比例函数的图象分布在第二、四象限,
∴,
解得,
故选:B.
4.D
解:∵k=﹣6<0,
∴在每个象限内y随x的增大而增大,
∵|y|≥3,
∴y≤﹣3或y≥3,
当y≤﹣3,即,
解得0<x≤2,
当y≥3时,,
解得﹣2≤x<0,
故当|y|≥3时,x的取值范围是﹣2≤x<0或0<x≤2,
故选D.
5.C
解:设y=(k≠0),
∵当x=2时,y=20,
∴k=2×20=40,
∴y=,
当x=1时,y=40,
则y与x的函数图象大致是C,
故选:C.
6.D
∵反比例函数(a是常数)的图象所在的每一个象限内,y随x增大而减小,
∴a-2>0,
解得a>2,
故选D.
7.C
∵k=-3<0,
∴函数图象位于第二、四象限,故B选项错误;
∵1×3=3≠-3,
∴函数图象不经过点(1,3),故A选项错误;
∵根据反比例函数的性质在函数图象的每一个象限内,y随x的增大而增大,
∴当时,y随x的增大而增大,故C选项正确;
当时,但是当时,故D选项错误;
故选:C.
8.A
解:∵点P(2,﹣2)在反比例函数的图象上,
∴
A. (﹣4,1),,故该选项正确,符合题意,
B. (1,4),,故该选项不符合题意,
C. (﹣2,﹣2),,故该选项不符合题意,
D. (4,),,故该选项不符合题意,
故选A
9.B
解:设点A的坐标为(x,y)
点A在第二象限
∴x<0,y>0
∴xy=-4
∵A是反比例函数 的图像上一点
∴k=xy=-4
故选:B
10.B
解:设P(x,y),根据题意xy=6,PA=y,OA=x,
∵PA⊥x轴于点A,
∴
=
=3,
故选:B.
11.A
解:∵k=-6<0,
∴图象位于第二、四象限,在每一象限内,y随x的增大而增大,
∴y2>0,y3<y1<0,
∴y3<y1<y2,
故选:A.
12.D
反比例函数经过二、四象限,
,
一次函数经过二、三、四象限,
,
,
故选:D.
13.
解:∵同一象限内的两点A(3,n),B(n﹣4,n+3)均在反比例函数的图象上,
∴k=3n=(n﹣4)(n+3),
解得n=6或n=﹣2,
∵n=﹣2时,A(3,﹣2),B(﹣6,1),
∴A、B不在同一象限,故n=﹣2舍去,
∵k=3n=18,
∴,
故答案为:y=.
14.y1>y2## y2< y1
∵
∴函数()的图象分布在第一、三象限,在每一象限,y随x的增大而减小,
∵﹣2<-1,
∴y1>y2
故答案为:y1>y2
15.-1
解:如图,过点A作
∵是等腰直角三角形,
∴
∴D点坐标为,A点坐标为
将A点坐标代入中,得
解得
故答案为:.
16.
解:设,
点是双曲线在第二象限的分支上的任意一点,点、、分别是点关于轴、原点、轴的对称点,
,
四边形为矩形,
四边形的面积为:,
又点在双曲线上,
,
四边形的面积为:.
故答案为:4.
17.(1)反比例函数的解析式为(x>0),E(4,4).
(2)点P的坐标为(0,).
解:(1)
∵点D是边AB的中点,AB=4,
∴AD=2,
∵四边形OABC是矩形,BC=8,
∴D(2,8),
∵反比例函数(x>0)的图象经过点D,
∴k=2×8=16,
∴反比例函数的解析式为(x>0),
当x=4时,y=4,
∴E(4,4).
(2)
如图,作点D关于y轴的对称点D′,连接D′E交y轴于P,连接PD,
此时,△PDE的周长最小,
∵点D的坐标为(2,8),
∴点D′的坐标为(-2,8),
设直线D′E的解析式为y=ax+b,
∴,
解得:,
∴直线D′E的解析式为,
令x=0,得y=,
∴点P的坐标为(0,).
18.(1)
(2)y1<y2
(3)3
解:(1)由,设反比例函数的解析式,则;
(2)由于反比例函数的性质是:在时,随的增大而减小,,则;
(3)连接,过点作轴,交轴于点,通过分割面积法求得.
(1)
解:,
;
;
(2)
解:,
函数的值在各自象限内随的增大而减小;
,
;
;
(3)
解:连接,过点作轴,
,
,;
,
.
19.(1),;
(2)的面积为.
解:∵反比例函数的图象经过点,
∴,
∴反比例函数的表达式为.
∵点在反比例函数图象上,
∴.
∴点A的坐标为.
∵一次函数的图象经过点和点,
∴,
解得:,
∴一次函数的表达式;
(2)
解:∵一次函数与y轴的交点为M,
∴当时,,
即点.
∴
,
∴的面积为.
20.(1)
(2)
(3)点P的坐标为或
解:(1)
点和点在图象上,
,,
即,
把,两点代入中得
解得:,
所以直线的解析式为:
(2)
由图象可得,当时,的解集为
(3)
由(1)得直线AB的解析式为,
当时,,
点坐标为
设P点坐标为,则
ADP的面积是6
×4×PD=6
PD=3
解得或
P的坐标为或
因此,点P的坐标为或时,ADP的面积是6.
答案第1页,共2页
一、单选题
1.反比例函数y=﹣的图象在第( )象限.
A.一、三象限 B.二、四象限 C.一、二象限 D.二、三象限
2.如果反比例函数y=的图象经过点(3,﹣4),那么k是( )
A.7 B.10 C.12 D.﹣12
3.若反比例函数的图象分布在第二、四象限,则k的取值范围是( )
A.k<2 B.k>2 C.k>1 D.k<1
4.已知反比例函数,当|y|≥3时,x的取值范围是( )
A.x≥2或x≤﹣2 B.﹣2≤x≤2
C.0<x≤2或x≤﹣2 D.﹣2≤x<0或0<x≤2
5.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
6.如果反比例函数(a是常数)的图象所在的每一个象限内,y随x增大而减小,那么a的取值范围是( )
A.a<0 B.a>0 C.a<2 D.a>2
7.下列关于反比例函数的结论中正确的是( )
A.图象过点(1,3) B.图象在一、三象限内
C.当时,y随x的增大而增大 D.当时
8.点P(2,﹣2)在反比例函数的图象上,则下列各点在该函数图象上的是( )
A.(﹣4,1) B.(1,4) C.(﹣2,﹣2) D.(4,)
9.如图,A是反比例函数y=的图象上一点,点C在x轴上,且S△ABC=2,则k的值为( )
A.4 B.﹣4 C.﹣2 D.2
10.如图,点P在双曲线第一象限的图象上,PA⊥x轴于点A,则的面积为( )
A.2 B.3 C.4 D.6
11.已知点(3,y1),(﹣2,y2),(2,y3)都在反比例函数的图象上,那么y1,y2与y3的大小关系是( )
A.y3<y1<y2 B.y3<y2<y1 C.y1<y2<y3 D.y1<y3<y2
12.一次函数与反比例函数上的图象在同一直角坐标系下的大致图象如图所示,则、b的取值范围是( )
A., B., C., D.,
二、填空题
13.已知同一象限内的两点A(3,n),B(n﹣4,n+3)均在反比例函数y=的图象上,则该反比例函数关系式为_____.
14.若点A(﹣2,y1)、B(﹣1,y2)在反比例函数y=图象上,则y1、y2大小关系是_______.
15.如在平面直角坐标系中,等腰直角△ABO如图放置,直角项点A在反比例函数的图形上,其中AB=AO,B(-2,0),则k=___.
16.如图所示,点是双曲线在第二象限的分支上的任意一点,点、、分别是点关于轴、原点、轴的对称点,则四边形的面积是__.
三、解答题
17.如图,在矩形OABC中,AB=4,BC=8,点D是边AB的中点,反比例函数(x>0)的图象经过点D,交BC边于点E.
(1)求反比例函数(x>0)的解析式和E点坐标;
(2)连结DE,在y轴上找一点P,使△PDE的周长最小,求出此时P的坐标.
18.如图,点A、B在反比例函数的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为点C,且△AOC的面积为2
(1)求该反比例函数的解析式;
(2)若点(﹣a,y1),(﹣2a,y2)在该反比例函数的图象上,试比较y1与y2的大小;
(3)求△AOB的面积.
19.如图,一次函数(k为常数,)与反比例函数(m为常数,)的图象交于点和,与y轴交于点M.
(1)求一次函数与反比例函数的表达式;
(2)连接OA、OB,求△AOB的面积,
20.直线与反比例函数的图象分别交于点A(m,4)和点B(8,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当时,直接写出的解集;
(3)若点P是x轴上一动点,当△ADP的面积是6时,求出P点的坐标.
试卷第1页,共3页
参考答案:
1.B
解:∵反比例函数y=-中k=-1<0,
∴图象位于二、四象限,
故选:B.
2.D
解:∵反比例函数y=的图象经过点(3,﹣4),
∴-4=,
解得k=-12.
故选D.
3.B
解:∵反比例函数的图象分布在第二、四象限,
∴,
解得,
故选:B.
4.D
解:∵k=﹣6<0,
∴在每个象限内y随x的增大而增大,
∵|y|≥3,
∴y≤﹣3或y≥3,
当y≤﹣3,即,
解得0<x≤2,
当y≥3时,,
解得﹣2≤x<0,
故当|y|≥3时,x的取值范围是﹣2≤x<0或0<x≤2,
故选D.
5.C
解:设y=(k≠0),
∵当x=2时,y=20,
∴k=2×20=40,
∴y=,
当x=1时,y=40,
则y与x的函数图象大致是C,
故选:C.
6.D
∵反比例函数(a是常数)的图象所在的每一个象限内,y随x增大而减小,
∴a-2>0,
解得a>2,
故选D.
7.C
∵k=-3<0,
∴函数图象位于第二、四象限,故B选项错误;
∵1×3=3≠-3,
∴函数图象不经过点(1,3),故A选项错误;
∵根据反比例函数的性质在函数图象的每一个象限内,y随x的增大而增大,
∴当时,y随x的增大而增大,故C选项正确;
当时,但是当时,故D选项错误;
故选:C.
8.A
解:∵点P(2,﹣2)在反比例函数的图象上,
∴
A. (﹣4,1),,故该选项正确,符合题意,
B. (1,4),,故该选项不符合题意,
C. (﹣2,﹣2),,故该选项不符合题意,
D. (4,),,故该选项不符合题意,
故选A
9.B
解:设点A的坐标为(x,y)
点A在第二象限
∴x<0,y>0
∴xy=-4
∵A是反比例函数 的图像上一点
∴k=xy=-4
故选:B
10.B
解:设P(x,y),根据题意xy=6,PA=y,OA=x,
∵PA⊥x轴于点A,
∴
=
=3,
故选:B.
11.A
解:∵k=-6<0,
∴图象位于第二、四象限,在每一象限内,y随x的增大而增大,
∴y2>0,y3<y1<0,
∴y3<y1<y2,
故选:A.
12.D
反比例函数经过二、四象限,
,
一次函数经过二、三、四象限,
,
,
故选:D.
13.
解:∵同一象限内的两点A(3,n),B(n﹣4,n+3)均在反比例函数的图象上,
∴k=3n=(n﹣4)(n+3),
解得n=6或n=﹣2,
∵n=﹣2时,A(3,﹣2),B(﹣6,1),
∴A、B不在同一象限,故n=﹣2舍去,
∵k=3n=18,
∴,
故答案为:y=.
14.y1>y2## y2< y1
∵
∴函数()的图象分布在第一、三象限,在每一象限,y随x的增大而减小,
∵﹣2<-1,
∴y1>y2
故答案为:y1>y2
15.-1
解:如图,过点A作
∵是等腰直角三角形,
∴
∴D点坐标为,A点坐标为
将A点坐标代入中,得
解得
故答案为:.
16.
解:设,
点是双曲线在第二象限的分支上的任意一点,点、、分别是点关于轴、原点、轴的对称点,
,
四边形为矩形,
四边形的面积为:,
又点在双曲线上,
,
四边形的面积为:.
故答案为:4.
17.(1)反比例函数的解析式为(x>0),E(4,4).
(2)点P的坐标为(0,).
解:(1)
∵点D是边AB的中点,AB=4,
∴AD=2,
∵四边形OABC是矩形,BC=8,
∴D(2,8),
∵反比例函数(x>0)的图象经过点D,
∴k=2×8=16,
∴反比例函数的解析式为(x>0),
当x=4时,y=4,
∴E(4,4).
(2)
如图,作点D关于y轴的对称点D′,连接D′E交y轴于P,连接PD,
此时,△PDE的周长最小,
∵点D的坐标为(2,8),
∴点D′的坐标为(-2,8),
设直线D′E的解析式为y=ax+b,
∴,
解得:,
∴直线D′E的解析式为,
令x=0,得y=,
∴点P的坐标为(0,).
18.(1)
(2)y1<y2
(3)3
解:(1)由,设反比例函数的解析式,则;
(2)由于反比例函数的性质是:在时,随的增大而减小,,则;
(3)连接,过点作轴,交轴于点,通过分割面积法求得.
(1)
解:,
;
;
(2)
解:,
函数的值在各自象限内随的增大而减小;
,
;
;
(3)
解:连接,过点作轴,
,
,;
,
.
19.(1),;
(2)的面积为.
解:∵反比例函数的图象经过点,
∴,
∴反比例函数的表达式为.
∵点在反比例函数图象上,
∴.
∴点A的坐标为.
∵一次函数的图象经过点和点,
∴,
解得:,
∴一次函数的表达式;
(2)
解:∵一次函数与y轴的交点为M,
∴当时,,
即点.
∴
,
∴的面积为.
20.(1)
(2)
(3)点P的坐标为或
解:(1)
点和点在图象上,
,,
即,
把,两点代入中得
解得:,
所以直线的解析式为:
(2)
由图象可得,当时,的解集为
(3)
由(1)得直线AB的解析式为,
当时,,
点坐标为
设P点坐标为,则
ADP的面积是6
×4×PD=6
PD=3
解得或
P的坐标为或
因此,点P的坐标为或时,ADP的面积是6.
答案第1页,共2页
