2021-2022学年人教版数学九年级下册26.2实际问题与反比例函数同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册26.2实际问题与反比例函数同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 403.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 21:22:34 | ||
图片预览


文档简介
实际问题与反比例函数
一、单选题
1.为了更好地保护水资源,造福人类.某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V=Sh(V≠0).则S关于h的函数图象大致是( ).
A. B.
C. D.
2.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图所示,当气球内的气压大于144kPa时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
3.如图是一个闭合电路,其电源的电压为定值,电流(A)是电阻()的反比例函数.当时,.若电阻增大,则电源为( )
A.3A B.4A C.7A D.12A
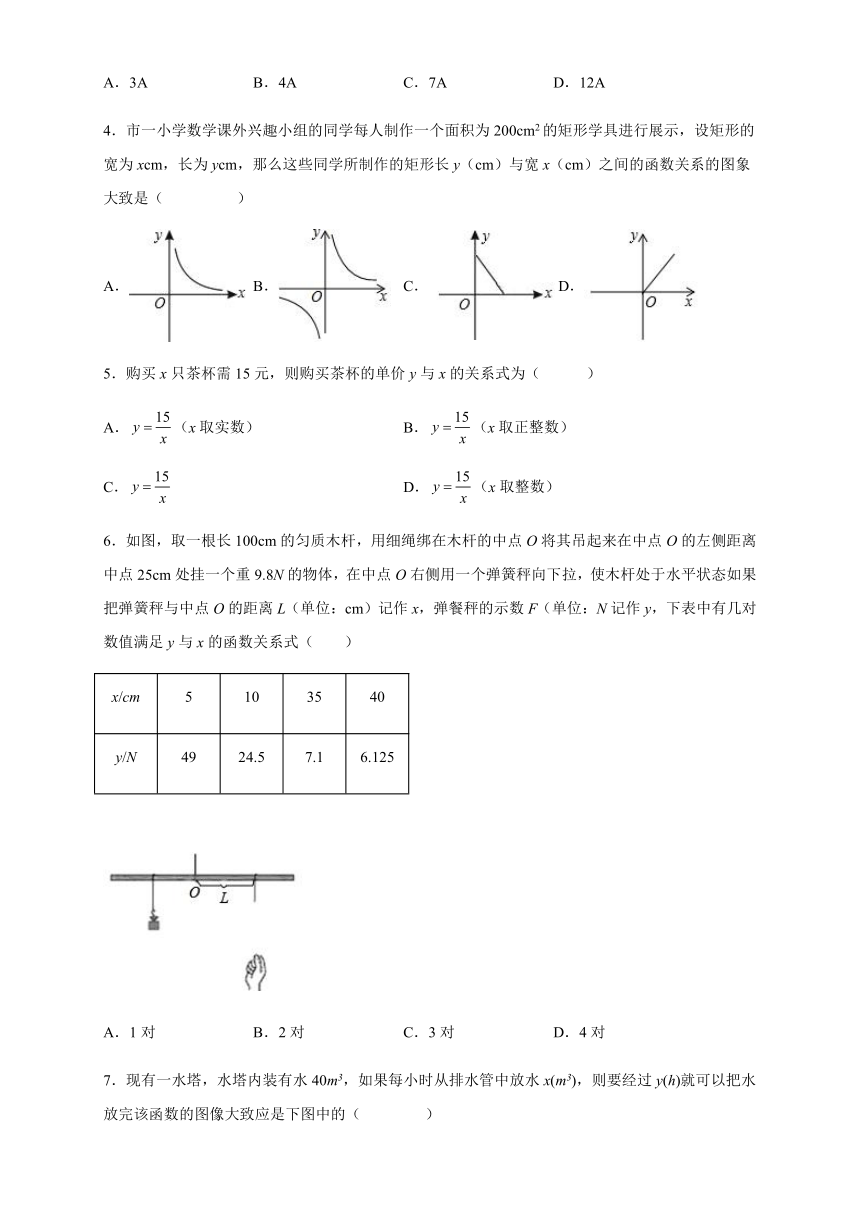
4.市一小学数学课外兴趣小组的同学每人制作一个面积为200cm2的矩形学具进行展示,设矩形的宽为xcm,长为ycm,那么这些同学所制作的矩形长y(cm)与宽x(cm)之间的函数关系的图象大致是( )
A. B. C. D.
5.购买x只茶杯需15元,则购买茶杯的单价y与x的关系式为( )
A.(x取实数) B.(x取正整数)
C. D.(x取整数)
6.如图,取一根长100cm的匀质木杆,用细绳绑在木杆的中点O将其吊起来在中点O的左侧距离中点25cm处挂一个重9.8N的物体,在中点O右侧用一个弹簧秤向下拉,使木杆处于水平状态如果把弹簧秤与中点O的距离L(单位:cm)记作x,弹餐秤的示数F(单位:N记作y,下表中有几对数值满足y与x的函数关系式( )
x/cm 5 10 35 40
y/N 49 24.5 7.1 6.125
A.1对 B.2对 C.3对 D.4对
7.现有一水塔,水塔内装有水40m3,如果每小时从排水管中放水x(m3),则要经过y(h)就可以把水放完该函数的图像大致应是下图中的( )
A. B. C. D.
8.如图,△ABC的边BC=y,BC边上的高AD=x,△ABC的面积为3,则y与x的函数图象大致是( )
A. B. C. D.
9.已知甲、乙两地相距40米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B. C. D.
10.某学校对教室采用药熏消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图),现测得药物8min燃毕,此时室内空气中每立方米含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是( )
A.10分钟 B.12分钟 C.14分钟 D.16分钟
11.某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强风是木板面积的反比例函数,其图象如图所示,当木板压强不超过时,木板的面积应为( )
A.不大于 B.不小于 C.不大于 D.不小于
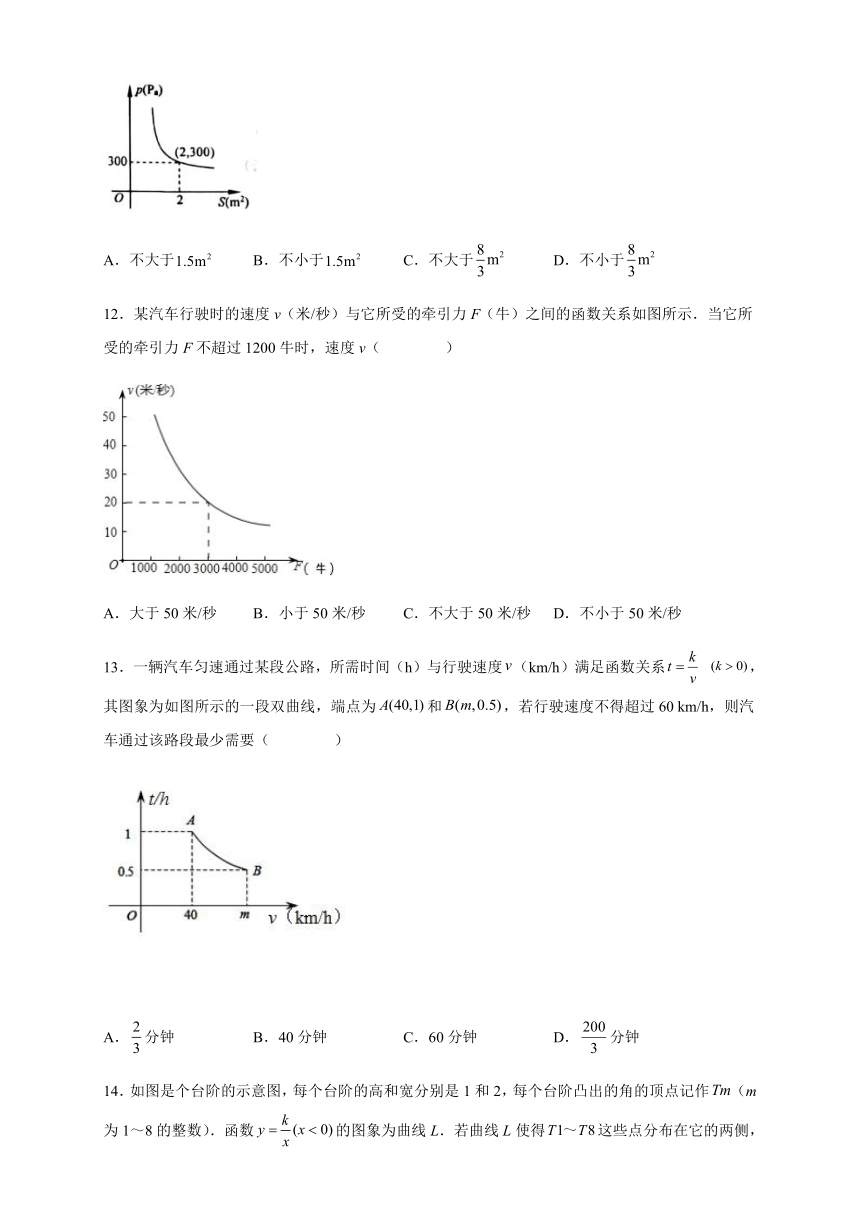
12.某汽车行驶时的速度v(米/秒)与它所受的牵引力F(牛)之间的函数关系如图所示.当它所受的牵引力F不超过1200牛时,速度v( )
A.大于50米/秒 B.小于50米/秒 C.不大于50米/秒 D.不小于50米/秒
13.一辆汽车匀速通过某段公路,所需时间(h)与行驶速度(km/h)满足函数关系 ,其图象为如图所示的一段双曲线,端点为和,若行驶速度不得超过60 km/h,则汽车通过该路段最少需要( )
A.分钟 B.40分钟 C.60分钟 D.分钟
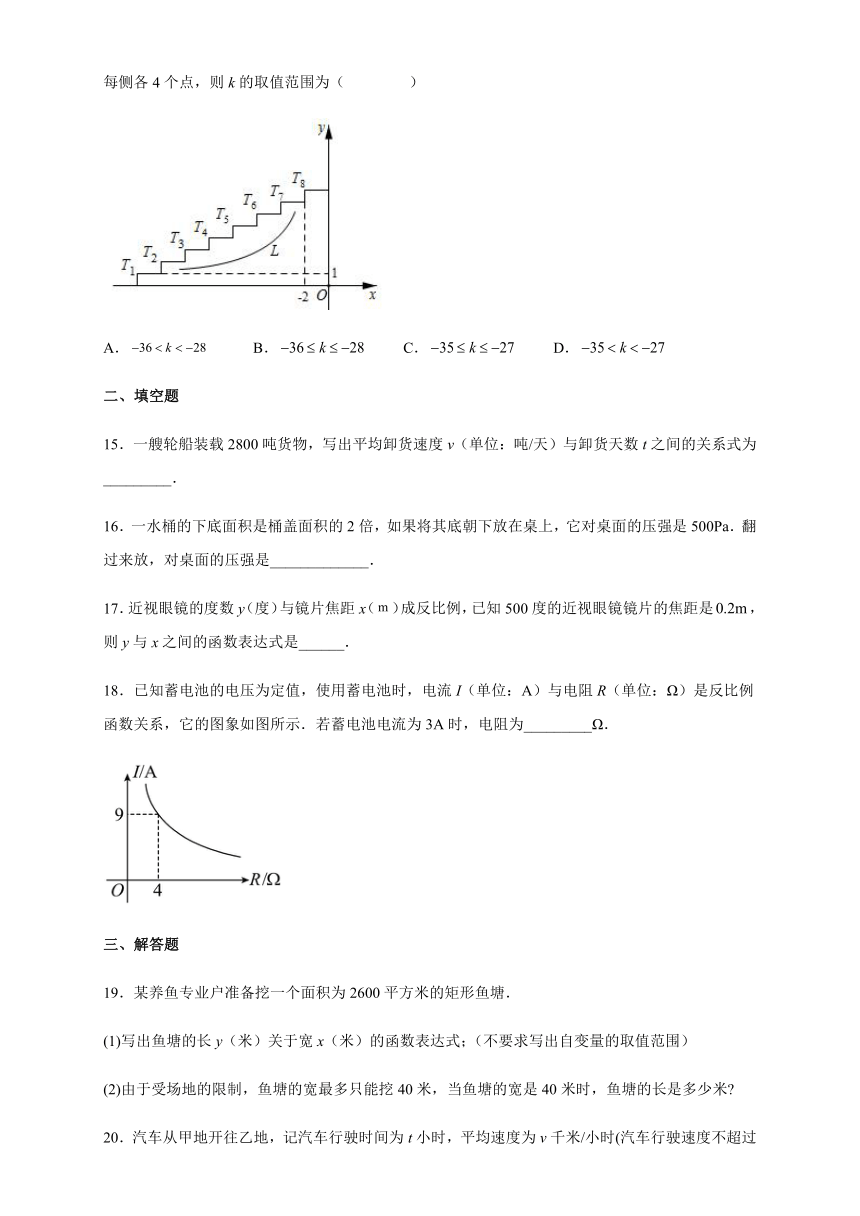
14.如图是个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作(m为1~8的整数).函数的图象为曲线L.若曲线L使得这些点分布在它的两侧,每侧各4个点,则k的取值范围为( )
A. B. C. D.
二、填空题
15.一艘轮船装载2800吨货物,写出平均卸货速度v(单位:吨/天)与卸货天数t之间的关系式为_________.
16.一水桶的下底面积是桶盖面积的2倍,如果将其底朝下放在桌上,它对桌面的压强是500Pa.翻过来放,对桌面的压强是_____________.
17.近视眼镜的度数y(度)与镜片焦距x()成反比例,已知500度的近视眼镜镜片的焦距是,则y与x之间的函数表达式是______.
18.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.若蓄电池电流为3A时,电阻为_________Ω.
三、解答题
19.某养鱼专业户准备挖一个面积为2600平方米的矩形鱼塘.
(1)写出鱼塘的长y(米)关于宽x(米)的函数表达式;(不要求写出自变量的取值范围)
(2)由于受场地的限制,鱼塘的宽最多只能挖40米,当鱼塘的宽是40米时,鱼塘的长是多少米
20.汽车从甲地开往乙地,记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) 75 80 85 90 95
t(小时) 4.00 3.75 3.53 3.33 3.16
(1)根据表中的数据,分析说明平均速度v(千米/小时)关于行驶时间t(小时)的函数关系,并求出其表达式;
(2)汽车上午8:00从甲地出发,能否在上午10:30之前到达乙地?请说明理由;
(3)若汽车到达乙地的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
21.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:,其图象为如图所示的一段曲线且端点为A(40,1)和B(m,0.5).
(1)求k和m的值;
(2)若行驶速度不得超过50km/h,则汽车通过该路段最少需要多少时间?
22.通过实验研究发现:初中生在体育课上运动能力指标(后简称指标)随上课时间的变化而变化.上课开始时,学生随着运动,指标开始增加,中间一段时间,指标保持平稳状态,随后随着体力的消耗,指标开始下降.指标y随时间x(分钟)变化的函数图象如图所示,当和时,图象是线段;当时,图象是反比例函数的一部分.
(1)请求出当和时,所对应的函数表达式:
(2)杨老师想在一节课上进行某项运动的教学需要18分钟,这项运动需要学生的运动能力指标不低于48才能达到较好的效果,他的教学设计能实现吗?请说明理由.
试卷第1页,共3页
参考答案:
1.C
解:略
2.B
解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为,
∵图象过点(1.5,64),
∴
解得:k=96,
即.
在第一象限内,P随V的增大而减小,
∴当时,.
故选:B.
3.B
解:,当时,.
当时,
故选B
4.A
解:∵xy=200
∴y= (x>0,y>0)
故选A.
5.B
解:由题意,得xy=15,
∴
x的值取正整数,
∴故选B.
6.C
解:由题意得,y x=25×9.8=245,
∴y;
当x=5时,y=49;
当x=10时,y=24.5;
当x=35时,y=7;
当x=40时,y=6.125;
有三对符合题意,
故答案选:C.
7.C
解:∵水塔内装有水40m3,如果每小时从排水管中放水x(m3),则要经过y(h)就可以把水放完,
∴y=,
∴x与y成反比例,四个选项中只有C是反比例函数的图象.
故选:C.
8.A
解:.的面积为3,
则
即
函数图像是双曲线
该反比例函数图像位于第一象限,
故选A
9.B
解:由题意得:vt=,
,
故选:B.
10.B
解:药物燃烧时y关于x的函数关系式为y=k1x(k1>0)代入(8,6)为6=8k1,
∴k1;
设药物燃烧后y关于x的函数关系式为y(k2>0)代入(8,6)为6,
∴k2=48
∴药物燃烧时y关于x的函数关系式为yx(0≤x≤8);药物燃烧后y关于x的函数关系式为y(x>8),
把y=3代入yx,得:x=4,
把y=3代入y,得:x=16,
∵16﹣4=12,
∴那么此次消毒的有效时间是12分钟,
故选:B.
11.B
解:设,
把代入,得,
,
.
由题意知,
,
即木板面积至少要有,
即不小于,
故选:B.
12.D
解:设v与F之间的函数关系式为v=,把(3000,20)代入得:P=60000,
∴v与F之间的函数关系式为,
把F=1200牛代入v==50(米/秒),
故当它所受的牵引力F不超过1200牛时,速度v不小于50米/秒.
故选:D.
13.B
解:由题意得,函数的解析式为t=函数经过点(40,1),
把(40,1)代入t=,得k=40,
则解析式为t=,
再把(m,0.5)代入t=,得m=80;
把v=60代入t=,得t=,
小时=40分钟,
则汽车通过该路段最少需要40分钟;
故选:B.
14.A
∵每个台阶的高和宽分别是1和2,
∴T1(-16,1),T2(-14,2),T3(-12,3),T4(-10,4),T5(-8,5),T6(-6,6),T7(-4,7),T8(-2,8),
∵L过点T1,
∴k=-16×1=-16,
若曲线L过点T2(-14,2),T7(-4,7)时,k=-14×2=-28,
若曲线L过点T3(-12,3),T6(-6,6)时,k=-12×3=-36,
若曲线L过点T4(-10,4),T5(-8,5)时,k=-40,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,
∴-36<k<-28,
故选:A.
15.v=
解:由题意得:2800=vt.
∴v=.
故答案为:v=.
16.1000Pa
解:设水桶的盖面积是S,则下底面积是2S,
根据题意可知,,
翻过来放,对桌面的压强帕,
故答案为:1000Pa
17.
解:设,
∵500度的近视眼镜镜片的焦距是,
∴,,
∴y与x之间的函数表达式是:,
故答案为:.
18.12
解:设该反比函数解析式为 ,
根据题意得:当 时, ,
∴ ,解得: ,
∴该反比函数解析式为,
∴当 时, ,
即电阻为12Ω.
故答案为:12
19.(1)
(2)当鱼塘的宽是40米时,鱼塘的长是65米
(1)
解:由矩形面积为2600平方米,
得到,
即;
(2)
解:当鱼塘的宽是40米时,
即米时,
代入,
得米,
则当鱼塘的宽是40米时,鱼塘的长为65米.
20.(1)平均速度v(千米/小时)关于行驶时间t(小时)成反比例函数关系,v=(t≥3)
(2)不能,理由见解析
(3)75≤v≤
(1)
解:由表格中的数据可以看出每一对v与t的对应值乘积为一定值,将每一对对应值作为点的坐标在平面直角坐标系中做出对应的图像是双曲线的一部分,
∴v是t的反比例函数,设,
∵v=75时,t=4,
∴k=75×4=300,
;
(2)
解:∵10.5-8=2.5,
∴t=2.5时,v==120,
∵120>100
∴汽车上午8:000从甲地出发,不能在上午10:30之前到乙地;
(3)
∵3.5≤t≤4,
,
答:平均速度v的取值范围是.
21.(1)40,80
(2)最少需要小时
(1)
由题意得,函数经过点(40,1),
,得k=40,
∴函数关系式为:
把(m,0.5)代入,得m=80;
(2)
把v=50代入,得,
∵t随v的增大而减小,
∴汽车通过该路段最少需要小时.
22.(1)分钟的函数解析式为,分钟的函数解析式为
(2)杨老师的教学设计能实现,见解析
(1)
解:设分钟的函数解析式为,分钟的函数解析式为,
将图象上的点(0,40)和(20,60)代入,B(20,60)代入
∴,,
∴,,
∴分钟的函数解析式为,分钟的函数解析式为;
(2)
解:能实现
将代入中得,
将代入中得,∵,
∴杨老师的教学设计能实现
答案第1页,共2页
一、单选题
1.为了更好地保护水资源,造福人类.某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V=Sh(V≠0).则S关于h的函数图象大致是( ).
A. B.
C. D.
2.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图所示,当气球内的气压大于144kPa时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
3.如图是一个闭合电路,其电源的电压为定值,电流(A)是电阻()的反比例函数.当时,.若电阻增大,则电源为( )
A.3A B.4A C.7A D.12A
4.市一小学数学课外兴趣小组的同学每人制作一个面积为200cm2的矩形学具进行展示,设矩形的宽为xcm,长为ycm,那么这些同学所制作的矩形长y(cm)与宽x(cm)之间的函数关系的图象大致是( )
A. B. C. D.
5.购买x只茶杯需15元,则购买茶杯的单价y与x的关系式为( )
A.(x取实数) B.(x取正整数)
C. D.(x取整数)
6.如图,取一根长100cm的匀质木杆,用细绳绑在木杆的中点O将其吊起来在中点O的左侧距离中点25cm处挂一个重9.8N的物体,在中点O右侧用一个弹簧秤向下拉,使木杆处于水平状态如果把弹簧秤与中点O的距离L(单位:cm)记作x,弹餐秤的示数F(单位:N记作y,下表中有几对数值满足y与x的函数关系式( )
x/cm 5 10 35 40
y/N 49 24.5 7.1 6.125
A.1对 B.2对 C.3对 D.4对
7.现有一水塔,水塔内装有水40m3,如果每小时从排水管中放水x(m3),则要经过y(h)就可以把水放完该函数的图像大致应是下图中的( )
A. B. C. D.
8.如图,△ABC的边BC=y,BC边上的高AD=x,△ABC的面积为3,则y与x的函数图象大致是( )
A. B. C. D.
9.已知甲、乙两地相距40米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B. C. D.
10.某学校对教室采用药熏消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图),现测得药物8min燃毕,此时室内空气中每立方米含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是( )
A.10分钟 B.12分钟 C.14分钟 D.16分钟
11.某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强风是木板面积的反比例函数,其图象如图所示,当木板压强不超过时,木板的面积应为( )
A.不大于 B.不小于 C.不大于 D.不小于
12.某汽车行驶时的速度v(米/秒)与它所受的牵引力F(牛)之间的函数关系如图所示.当它所受的牵引力F不超过1200牛时,速度v( )
A.大于50米/秒 B.小于50米/秒 C.不大于50米/秒 D.不小于50米/秒
13.一辆汽车匀速通过某段公路,所需时间(h)与行驶速度(km/h)满足函数关系 ,其图象为如图所示的一段双曲线,端点为和,若行驶速度不得超过60 km/h,则汽车通过该路段最少需要( )
A.分钟 B.40分钟 C.60分钟 D.分钟
14.如图是个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作(m为1~8的整数).函数的图象为曲线L.若曲线L使得这些点分布在它的两侧,每侧各4个点,则k的取值范围为( )
A. B. C. D.
二、填空题
15.一艘轮船装载2800吨货物,写出平均卸货速度v(单位:吨/天)与卸货天数t之间的关系式为_________.
16.一水桶的下底面积是桶盖面积的2倍,如果将其底朝下放在桌上,它对桌面的压强是500Pa.翻过来放,对桌面的压强是_____________.
17.近视眼镜的度数y(度)与镜片焦距x()成反比例,已知500度的近视眼镜镜片的焦距是,则y与x之间的函数表达式是______.
18.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.若蓄电池电流为3A时,电阻为_________Ω.
三、解答题
19.某养鱼专业户准备挖一个面积为2600平方米的矩形鱼塘.
(1)写出鱼塘的长y(米)关于宽x(米)的函数表达式;(不要求写出自变量的取值范围)
(2)由于受场地的限制,鱼塘的宽最多只能挖40米,当鱼塘的宽是40米时,鱼塘的长是多少米
20.汽车从甲地开往乙地,记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) 75 80 85 90 95
t(小时) 4.00 3.75 3.53 3.33 3.16
(1)根据表中的数据,分析说明平均速度v(千米/小时)关于行驶时间t(小时)的函数关系,并求出其表达式;
(2)汽车上午8:00从甲地出发,能否在上午10:30之前到达乙地?请说明理由;
(3)若汽车到达乙地的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
21.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:,其图象为如图所示的一段曲线且端点为A(40,1)和B(m,0.5).
(1)求k和m的值;
(2)若行驶速度不得超过50km/h,则汽车通过该路段最少需要多少时间?
22.通过实验研究发现:初中生在体育课上运动能力指标(后简称指标)随上课时间的变化而变化.上课开始时,学生随着运动,指标开始增加,中间一段时间,指标保持平稳状态,随后随着体力的消耗,指标开始下降.指标y随时间x(分钟)变化的函数图象如图所示,当和时,图象是线段;当时,图象是反比例函数的一部分.
(1)请求出当和时,所对应的函数表达式:
(2)杨老师想在一节课上进行某项运动的教学需要18分钟,这项运动需要学生的运动能力指标不低于48才能达到较好的效果,他的教学设计能实现吗?请说明理由.
试卷第1页,共3页
参考答案:
1.C
解:略
2.B
解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为,
∵图象过点(1.5,64),
∴
解得:k=96,
即.
在第一象限内,P随V的增大而减小,
∴当时,.
故选:B.
3.B
解:,当时,.
当时,
故选B
4.A
解:∵xy=200
∴y= (x>0,y>0)
故选A.
5.B
解:由题意,得xy=15,
∴
x的值取正整数,
∴故选B.
6.C
解:由题意得,y x=25×9.8=245,
∴y;
当x=5时,y=49;
当x=10时,y=24.5;
当x=35时,y=7;
当x=40时,y=6.125;
有三对符合题意,
故答案选:C.
7.C
解:∵水塔内装有水40m3,如果每小时从排水管中放水x(m3),则要经过y(h)就可以把水放完,
∴y=,
∴x与y成反比例,四个选项中只有C是反比例函数的图象.
故选:C.
8.A
解:.的面积为3,
则
即
函数图像是双曲线
该反比例函数图像位于第一象限,
故选A
9.B
解:由题意得:vt=,
,
故选:B.
10.B
解:药物燃烧时y关于x的函数关系式为y=k1x(k1>0)代入(8,6)为6=8k1,
∴k1;
设药物燃烧后y关于x的函数关系式为y(k2>0)代入(8,6)为6,
∴k2=48
∴药物燃烧时y关于x的函数关系式为yx(0≤x≤8);药物燃烧后y关于x的函数关系式为y(x>8),
把y=3代入yx,得:x=4,
把y=3代入y,得:x=16,
∵16﹣4=12,
∴那么此次消毒的有效时间是12分钟,
故选:B.
11.B
解:设,
把代入,得,
,
.
由题意知,
,
即木板面积至少要有,
即不小于,
故选:B.
12.D
解:设v与F之间的函数关系式为v=,把(3000,20)代入得:P=60000,
∴v与F之间的函数关系式为,
把F=1200牛代入v==50(米/秒),
故当它所受的牵引力F不超过1200牛时,速度v不小于50米/秒.
故选:D.
13.B
解:由题意得,函数的解析式为t=函数经过点(40,1),
把(40,1)代入t=,得k=40,
则解析式为t=,
再把(m,0.5)代入t=,得m=80;
把v=60代入t=,得t=,
小时=40分钟,
则汽车通过该路段最少需要40分钟;
故选:B.
14.A
∵每个台阶的高和宽分别是1和2,
∴T1(-16,1),T2(-14,2),T3(-12,3),T4(-10,4),T5(-8,5),T6(-6,6),T7(-4,7),T8(-2,8),
∵L过点T1,
∴k=-16×1=-16,
若曲线L过点T2(-14,2),T7(-4,7)时,k=-14×2=-28,
若曲线L过点T3(-12,3),T6(-6,6)时,k=-12×3=-36,
若曲线L过点T4(-10,4),T5(-8,5)时,k=-40,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,
∴-36<k<-28,
故选:A.
15.v=
解:由题意得:2800=vt.
∴v=.
故答案为:v=.
16.1000Pa
解:设水桶的盖面积是S,则下底面积是2S,
根据题意可知,,
翻过来放,对桌面的压强帕,
故答案为:1000Pa
17.
解:设,
∵500度的近视眼镜镜片的焦距是,
∴,,
∴y与x之间的函数表达式是:,
故答案为:.
18.12
解:设该反比函数解析式为 ,
根据题意得:当 时, ,
∴ ,解得: ,
∴该反比函数解析式为,
∴当 时, ,
即电阻为12Ω.
故答案为:12
19.(1)
(2)当鱼塘的宽是40米时,鱼塘的长是65米
(1)
解:由矩形面积为2600平方米,
得到,
即;
(2)
解:当鱼塘的宽是40米时,
即米时,
代入,
得米,
则当鱼塘的宽是40米时,鱼塘的长为65米.
20.(1)平均速度v(千米/小时)关于行驶时间t(小时)成反比例函数关系,v=(t≥3)
(2)不能,理由见解析
(3)75≤v≤
(1)
解:由表格中的数据可以看出每一对v与t的对应值乘积为一定值,将每一对对应值作为点的坐标在平面直角坐标系中做出对应的图像是双曲线的一部分,
∴v是t的反比例函数,设,
∵v=75时,t=4,
∴k=75×4=300,
;
(2)
解:∵10.5-8=2.5,
∴t=2.5时,v==120,
∵120>100
∴汽车上午8:000从甲地出发,不能在上午10:30之前到乙地;
(3)
∵3.5≤t≤4,
,
答:平均速度v的取值范围是.
21.(1)40,80
(2)最少需要小时
(1)
由题意得,函数经过点(40,1),
,得k=40,
∴函数关系式为:
把(m,0.5)代入,得m=80;
(2)
把v=50代入,得,
∵t随v的增大而减小,
∴汽车通过该路段最少需要小时.
22.(1)分钟的函数解析式为,分钟的函数解析式为
(2)杨老师的教学设计能实现,见解析
(1)
解:设分钟的函数解析式为,分钟的函数解析式为,
将图象上的点(0,40)和(20,60)代入,B(20,60)代入
∴,,
∴,,
∴分钟的函数解析式为,分钟的函数解析式为;
(2)
解:能实现
将代入中得,
将代入中得,∵,
∴杨老师的教学设计能实现
答案第1页,共2页
