2021-2022学年苏科版七年级数学下册第7章平面图形的认识(二)单元综合测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册第7章平面图形的认识(二)单元综合测试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 384.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 21:39:33 | ||
图片预览



文档简介
2021-2022学年苏科版七年级数学下册《第7章平面图形的认识(二)》
单元综合测试题(附答案)
一.选择题(共8小题,满分40分)
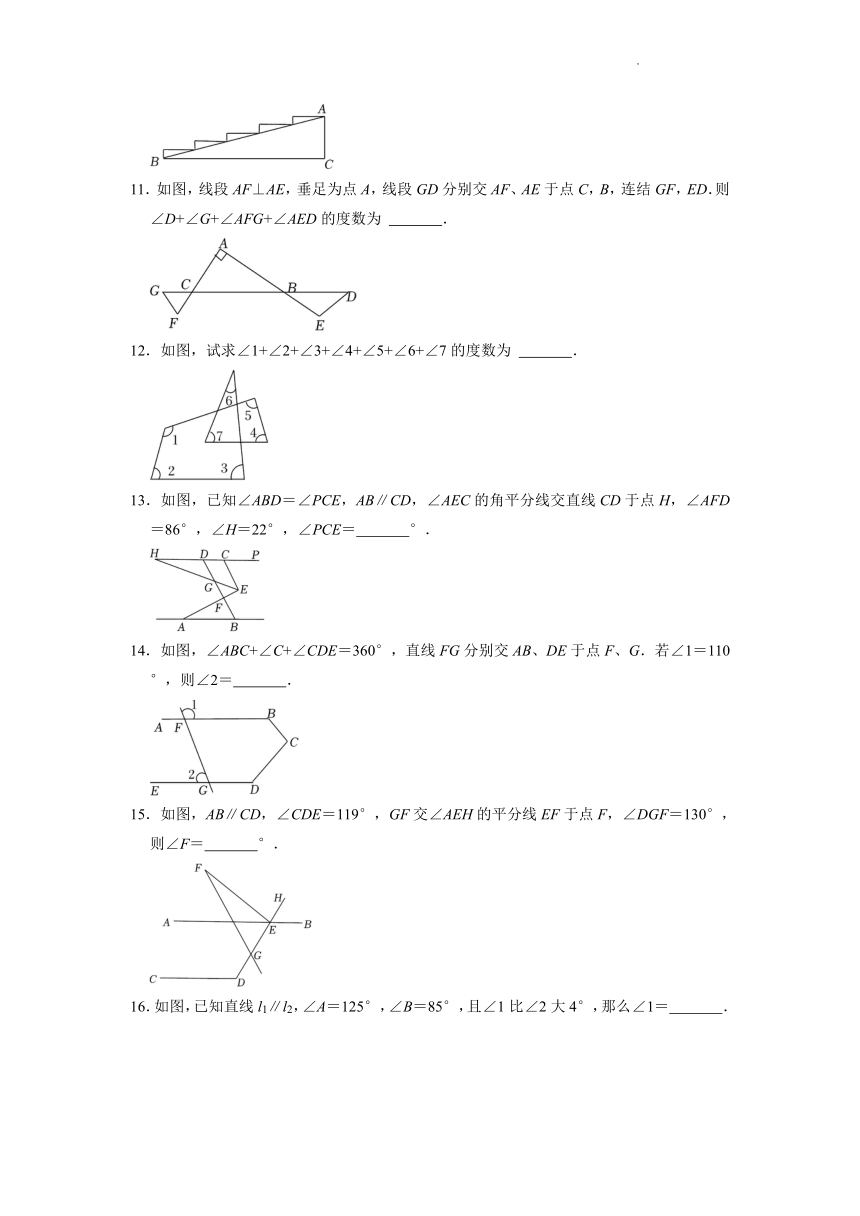
1.在同一平面内,将两个完全相同的三角板如图所示摆放(直角边重合),可以画出两条互相平行的直线a,b.这样操作的依据是( )
A.内错角相等,两直线平行
B.同位角相等,两直线平行
C.两直线平行,内错角相等
D.两直线平行,同位角相等
2.如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为( )
A.3 B.4 C.5 D.6
3.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6+∠4=180°;⑥∠5+∠1=180°,其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
4.如图,AD∥CE,∠ABC=110°,则∠2﹣∠1的度数是( )
A.50° B.60° C.70° D.110°
5.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外面时,此时测得∠1=112°,∠A=40°,则∠2的度数为( )
A.32° B.33° C.34° D.38°
6.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80° B.85° C.90° D.95°
7.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,∠1=30°,则∠2的度数是( )
A.50° B.60° C.65° D.70°
8.如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.240° B.360° C.540° D.720°
二.填空题(共8小题,满分40分)
9.如图,AB∥CD,AD⊥AC,∠BAD=40°,则∠ACD等于 °.
10.如图所示,要在竖直高AC为3米,水平宽BC为12米的楼梯表面铺地毯,地毯的长度至少需要 米.
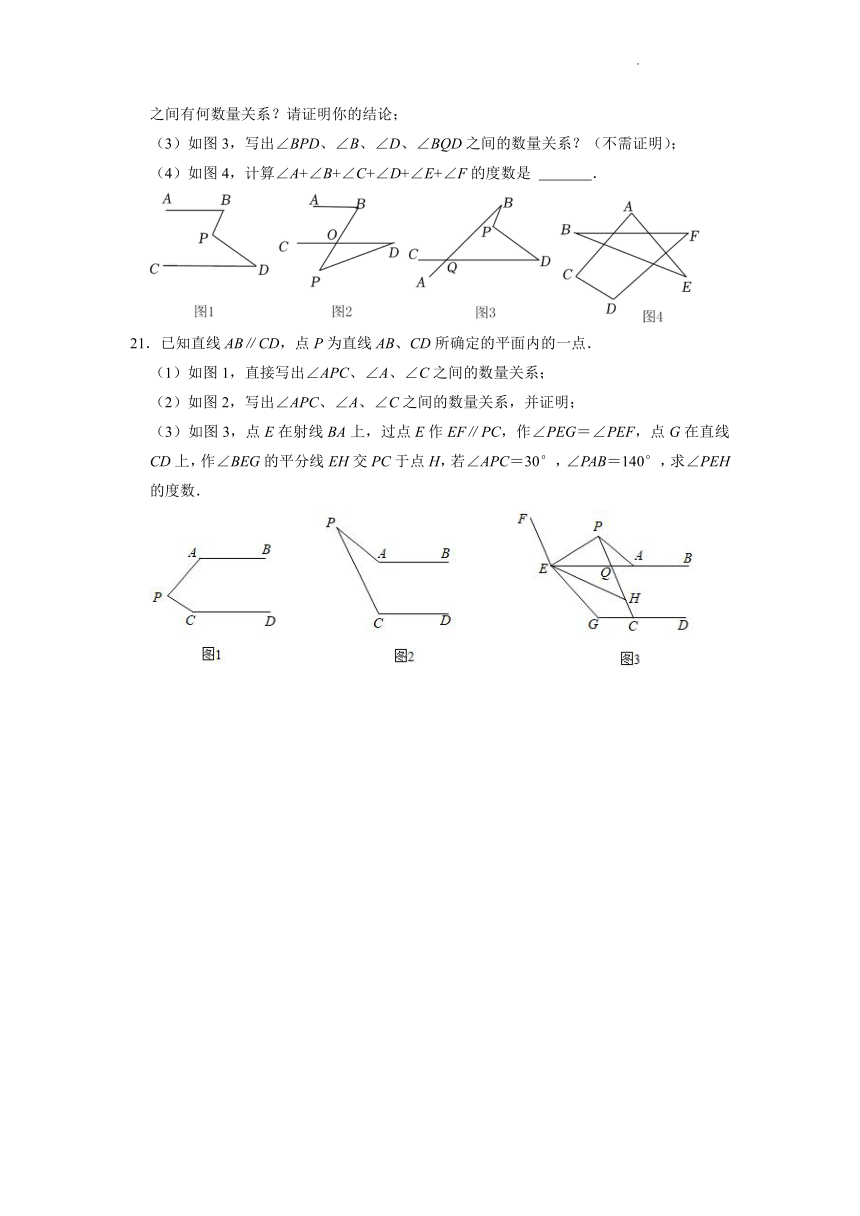
11.如图,线段AF⊥AE,垂足为点A,线段GD分别交AF、AE于点C,B,连结GF,ED.则∠D+∠G+∠AFG+∠AED的度数为 .
12.如图,试求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数为 .
13.如图,已知∠ABD=∠PCE,AB∥CD,∠AEC的角平分线交直线CD于点H,∠AFD=86°,∠H=22°,∠PCE= °.
14.如图,∠ABC+∠C+∠CDE=360°,直线FG分别交AB、DE于点F、G.若∠1=110°,则∠2= .
15.如图,AB∥CD,∠CDE=119°,GF交∠AEH的平分线EF于点F,∠DGF=130°,则∠F= °.
16.如图,已知直线l1∥l2,∠A=125°,∠B=85°,且∠1比∠2大4°,那么∠1= .
三.解答题(共5小题,满分40分)
17.如图,已知点D,E分别在△ABC的边AB,AC上,DE∥BC.
(1)若∠ABC=80°,∠AED=40°,求∠A的度数;
(2)若∠BFD+∠CEF=180°,求证:∠EDF=∠C.
18.如图:已知,∠A=120°,∠ABC=60°,BD⊥DC于点D,EF⊥DC于点F,
求证:(1)AD∥BC;
(2)∠1=∠2.
19.如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=140°,∠B=45°,求∠AGF的度数.
20.平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD的度数;
(2)如图2,在AB∥CD的前提下,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(3)如图3,写出∠BPD、∠B、∠D、∠BQD之间的数量关系?(不需证明);
(4)如图4,计算∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
21.已知直线AB∥CD,点P为直线AB、CD所确定的平面内的一点.
(1)如图1,直接写出∠APC、∠A、∠C之间的数量关系;
(2)如图2,写出∠APC、∠A、∠C之间的数量关系,并证明;
(3)如图3,点E在射线BA上,过点E作EF∥PC,作∠PEG=∠PEF,点G在直线CD上,作∠BEG的平分线EH交PC于点H,若∠APC=30°,∠PAB=140°,求∠PEH的度数.
参考答案
一.选择题(共8小题,满分40分)
1.解:如图:
∵两个完全相同的三角板,
∴∠1=∠2,
而∠1、∠2是一对内错角,
∴a∥b,
故选:A.
2.解:由平移的性质可知,BE=CF,
∵BF=8,EC=2,
∴BE+CF=8﹣2=6,
∴BE=CF=3,
∴平移的距离为3,
故选:A.
3.解:①∠1=∠2,不能判定l1∥l2;
②∠4=∠5,能判定l1∥l2;
③∠2+∠5=180°,不能判定l1∥l2;
④∠1=∠3,能判定l1∥l2;
⑤∠6+∠4=180°,不能判定l1∥l2;
⑥∠5+∠1=180°,不能判定l1∥l2;
故选:D.
4.解:如图,作BF∥AD,
∵AD∥CE,
∴AD∥BF∥EC,
∴∠1=∠3,∠4+∠2=180°,∠3+∠4=110°,
∴∠1+∠4=110°,
∴∠2﹣∠1=70°.
故选:C.
5.解:如图,设A′D与AD交于点O,
∵∠A=40°,
∴∠A′=∠A=40°,
∵∠1=∠DOA+∠A,∠1=112°,
∴∠DOA=∠1﹣∠A=112°﹣40°=72°,
∵∠DOA=∠2+∠A′,
∴∠2=∠DOA﹣∠A′=72°﹣40°=32°.
故选:A.
6.解:过C作CM∥AB,
∵AB∥DE,
∴AB∥CM∥DE,
∴∠1+∠B=180°,∠2=∠D=35°,
∵∠B=130°,
∴∠1=50°,
∴∠BCD=∠1+∠2=85°,
故选:B.
7.解:如图,延长FA,由折叠的性质,可得∠3=∠1=30°,
∴∠4=180°﹣30°﹣30°=120°,
∵CD∥BE,BE∥AF,
∴∠ACD=∠4=120°,
又∵AC∥BD,
∴∠2=180°﹣∠ACD=180°﹣120°=60°.
故选:B.
8.解:如图,AC、DF与BE分别相交于点M、N,
在四边形NMCD中,∠MND+∠CMN+∠C+∠D=360°,
∵∠CMN=∠A+∠E,∠MND=∠B+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵AD⊥AC,
∴∠CAD=90°,
∵∠BAD=40°,
∴∠BAC=∠CAD+∠BAD=130°,
∵AB∥CD,
∴∠ACD+∠BAC=180°,
∴∠ACD=180°﹣∠BAC=50°.
故答案为:50.
10.解:由题意可得:
地毯的水平长度=BC=12米,地毯的垂直长度=AC=3米,
∴地毯的长度至少需要:12+3=15米,
故答案为:15.
11.解:∵∠A+∠ACB+∠ABC=180°,∠A=90°,
∴∠ACB+∠ABC=90°,
∵∠GCF=∠ACB,∠DBE=∠ABC,
∴∠GCF+∠DBE=90°,
∵∠G+∠F+∠GCF=∠D+∠B+∠DBE=180°,
∴∠G+∠F+∠GCF+∠D+∠B+∠DBE=360°,
∴∠D+∠G+∠AFG+∠AED=270°,
故答案为:270°.
12.解:如图,
根据四边形的内角和可得,∠1+∠2+∠3+∠8=360°,∠4+∠5+∠9+∠10=360°,
∵∠9=∠6+∠7,∠8+∠10=180°,
∴∠1+∠2+∠3+∠8+∠4+∠5+∠10+∠6+∠7=720°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
故答案为:540°.
13.解:∵AB∥CD,
∴∠ABD=∠PDB,
∵∠ABD=∠PCE,
∴∠PDB=∠PCE,
∴BD∥CE,
∴∠CEG=∠DGH,
∵EH平分∠AEC,
∴∠CEH=∠AEH,
∵∠DGH=∠EGF,
∴∠EGF=∠GEF,
∵∠AFD=∠AEG+∠EGF=2∠EGF=86°,
∴∠EGF=43°,
∴∠DGH=43°,
∴∠PCE=∠PDG=∠H+∠DGH=65°,
故答案为:65.
14.解:如图,过点C作CH∥AB,
则∠ABC+∠BCH=180°,
∵∠ABC+∠C+∠CDE=360°,即∠ABC+∠BCH+∠DCH+∠CDE=360°,
∴∠DCH+∠CDE=180°,
∴CH∥DE,
∴AB∥DE,
∴∠DGF=∠1=110°,
∴∠2=180°﹣110°=70°,
故答案为:70°.
15.解:∵AB∥CD,∠CDE=119°,
∴∠AEH=∠CDE=119°,
∵EF平分∠AEH,
∴∠FEH=∠AEH=59.5°,
∵∠DGF=130°,
∴∠FGE=180°﹣∠DGF=50°,
∵∠FEH是△EFG的外角,
∴∠F=∠FEH﹣∠FGE=9.5°.
故答案为:9.5.
16.解:如图,过点A作l1的平行线AC,过点B作l2的平行线BD,
则∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°,
∵∠1=∠2+4°,
∴∠1=17°,
故答案为:17°.
三.解答题(共5小题,满分40分)
17.(1)解:∵DE∥BC(已知),
∴∠C=∠AED(两直线平行,同位角相等).
∵∠A+∠ABC+∠C=180°(三角形内角和定理),
∴∠A=180°﹣∠ABC﹣∠C=180°﹣∠ABC﹣∠AED(等式的性质).
∵∠AED=40°,∠ABC=80°(已知),
∴∠A=180°﹣40°﹣80°=60°(等式的性质);
(2)证明:∵∠BFD+∠DFE=180°(平角定义),
∠BFD+∠CEF=180°(已知),
∴∠DFE=∠CEF(同角的补角相等).
∴DF∥AC(内错角相等,两直线平行).
∴∠EDF=∠AED(两直线平行,内错角相等).
∵DE∥BC(已知),
∴∠AED=∠C(两直线平行,同位角相等).
∴∠EDF=∠C(等量代换).
18.证明:(1)∵∠A=120°,∠ABC=60°,
∴∠A+∠ABC=180°.
∴AD∥BC;
(2)∵AD∥BC,
∴∠1=∠DBC.
∵BD⊥DC,EF⊥DC,
∴∠BDF=90°,∠EFC=90°.
∴∠BDF=∠EFC=90°.
∴BD∥EF.
∴∠2=∠DBC.
∴∠1=∠2.
19.解:∵CE平分∠ACD,∠ACD=140°,
∴∠ACE=×∠ACD=×140°=70°,∠ACB=180°﹣∠ACD=40°,
∵FG∥CE,
∴∠AFG=∠ACE=70°,
∵∠FAG=∠B+∠ACB=85°,
∴∠ADF=180°﹣∠AFG﹣∠FAG=25°.
故∠AGF的度数是25°.
20.解:(1)如图1,过P点作PO∥AB,
∵AB∥CD,
∴CD∥PO∥AB,
∴∠BPO=∠B,∠OPD=∠D,
∵∠BPD=∠BPO+∠OPD,
∴∠BPD=∠B+∠D.
∵∠B=50°,∠D=30°,
∴∠BPD=∠B+∠D=50°+30°=80°;
(2)∠B=∠D+∠BPD,
∵AB∥CD,
∴∠B=∠BOD,
∵∠BOD=∠D+∠BPD,
∴∠B=∠D+∠BPD;
(3)∠BPD=∠B+∠D+∠BQD.
证明:如图3,连接QP并延长,
∵∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQE,
∴∠BPE+DPE=∠B+∠BQE+∠D+∠DQE,即∠BPD=∠B+∠D+∠BQD.
(4)∵∠CMN=∠A+∠E,∠DNB=∠B+∠F,
又∵∠C+∠D+∠CMN+∠DNM=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.
21.解:(1)∠A+∠C+∠APC=360°
如图1所示,过点P作PQ∥AB,
∴∠A+∠APQ=180°,
∵AB∥CD,
∴PQ∥CD,
∴∠C+∠CPQ=180°,
∴∠A+∠APQ+∠C+∠CPQ=360°,即∠A+∠C+∠APC=360°;
(2)∠APC=∠A+∠C,
如图2,作PQ∥AB,
∴∠A=∠APQ,
∵AB∥CD,
∴PQ∥CD,
∴∠C=∠CPQ,
∵∠APC=∠APQ﹣∠CPQ,
∴∠APC=∠A﹣∠C;
(3)由(2)知,∠APC=∠PAB﹣∠PCD,
∵∠APC=30°,∠PAB=140°,
∴∠PCD=110°,
∵AB∥CD,
∴∠PQB=∠PCD=110°,
∵EF∥BC,
∴∠BEF=∠PQB=110°,
∵EF∥BC,
∴∠BEF=∠PQB=110°,
∵∠PEG=∠PEF,
∴∠PEG=∠FEG,
∵EH平分∠BEG,
∴∠GEH=∠BEG,
∴∠PEH=∠PEG﹣∠GEH
=∠FEG﹣∠BEG
=∠BEF
=55°.
单元综合测试题(附答案)
一.选择题(共8小题,满分40分)
1.在同一平面内,将两个完全相同的三角板如图所示摆放(直角边重合),可以画出两条互相平行的直线a,b.这样操作的依据是( )
A.内错角相等,两直线平行
B.同位角相等,两直线平行
C.两直线平行,内错角相等
D.两直线平行,同位角相等
2.如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为( )
A.3 B.4 C.5 D.6
3.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6+∠4=180°;⑥∠5+∠1=180°,其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
4.如图,AD∥CE,∠ABC=110°,则∠2﹣∠1的度数是( )
A.50° B.60° C.70° D.110°
5.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外面时,此时测得∠1=112°,∠A=40°,则∠2的度数为( )
A.32° B.33° C.34° D.38°
6.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80° B.85° C.90° D.95°
7.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,∠1=30°,则∠2的度数是( )
A.50° B.60° C.65° D.70°
8.如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.240° B.360° C.540° D.720°
二.填空题(共8小题,满分40分)
9.如图,AB∥CD,AD⊥AC,∠BAD=40°,则∠ACD等于 °.
10.如图所示,要在竖直高AC为3米,水平宽BC为12米的楼梯表面铺地毯,地毯的长度至少需要 米.
11.如图,线段AF⊥AE,垂足为点A,线段GD分别交AF、AE于点C,B,连结GF,ED.则∠D+∠G+∠AFG+∠AED的度数为 .
12.如图,试求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数为 .
13.如图,已知∠ABD=∠PCE,AB∥CD,∠AEC的角平分线交直线CD于点H,∠AFD=86°,∠H=22°,∠PCE= °.
14.如图,∠ABC+∠C+∠CDE=360°,直线FG分别交AB、DE于点F、G.若∠1=110°,则∠2= .
15.如图,AB∥CD,∠CDE=119°,GF交∠AEH的平分线EF于点F,∠DGF=130°,则∠F= °.
16.如图,已知直线l1∥l2,∠A=125°,∠B=85°,且∠1比∠2大4°,那么∠1= .
三.解答题(共5小题,满分40分)
17.如图,已知点D,E分别在△ABC的边AB,AC上,DE∥BC.
(1)若∠ABC=80°,∠AED=40°,求∠A的度数;
(2)若∠BFD+∠CEF=180°,求证:∠EDF=∠C.
18.如图:已知,∠A=120°,∠ABC=60°,BD⊥DC于点D,EF⊥DC于点F,
求证:(1)AD∥BC;
(2)∠1=∠2.
19.如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=140°,∠B=45°,求∠AGF的度数.
20.平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD的度数;
(2)如图2,在AB∥CD的前提下,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(3)如图3,写出∠BPD、∠B、∠D、∠BQD之间的数量关系?(不需证明);
(4)如图4,计算∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
21.已知直线AB∥CD,点P为直线AB、CD所确定的平面内的一点.
(1)如图1,直接写出∠APC、∠A、∠C之间的数量关系;
(2)如图2,写出∠APC、∠A、∠C之间的数量关系,并证明;
(3)如图3,点E在射线BA上,过点E作EF∥PC,作∠PEG=∠PEF,点G在直线CD上,作∠BEG的平分线EH交PC于点H,若∠APC=30°,∠PAB=140°,求∠PEH的度数.
参考答案
一.选择题(共8小题,满分40分)
1.解:如图:
∵两个完全相同的三角板,
∴∠1=∠2,
而∠1、∠2是一对内错角,
∴a∥b,
故选:A.
2.解:由平移的性质可知,BE=CF,
∵BF=8,EC=2,
∴BE+CF=8﹣2=6,
∴BE=CF=3,
∴平移的距离为3,
故选:A.
3.解:①∠1=∠2,不能判定l1∥l2;
②∠4=∠5,能判定l1∥l2;
③∠2+∠5=180°,不能判定l1∥l2;
④∠1=∠3,能判定l1∥l2;
⑤∠6+∠4=180°,不能判定l1∥l2;
⑥∠5+∠1=180°,不能判定l1∥l2;
故选:D.
4.解:如图,作BF∥AD,
∵AD∥CE,
∴AD∥BF∥EC,
∴∠1=∠3,∠4+∠2=180°,∠3+∠4=110°,
∴∠1+∠4=110°,
∴∠2﹣∠1=70°.
故选:C.
5.解:如图,设A′D与AD交于点O,
∵∠A=40°,
∴∠A′=∠A=40°,
∵∠1=∠DOA+∠A,∠1=112°,
∴∠DOA=∠1﹣∠A=112°﹣40°=72°,
∵∠DOA=∠2+∠A′,
∴∠2=∠DOA﹣∠A′=72°﹣40°=32°.
故选:A.
6.解:过C作CM∥AB,
∵AB∥DE,
∴AB∥CM∥DE,
∴∠1+∠B=180°,∠2=∠D=35°,
∵∠B=130°,
∴∠1=50°,
∴∠BCD=∠1+∠2=85°,
故选:B.
7.解:如图,延长FA,由折叠的性质,可得∠3=∠1=30°,
∴∠4=180°﹣30°﹣30°=120°,
∵CD∥BE,BE∥AF,
∴∠ACD=∠4=120°,
又∵AC∥BD,
∴∠2=180°﹣∠ACD=180°﹣120°=60°.
故选:B.
8.解:如图,AC、DF与BE分别相交于点M、N,
在四边形NMCD中,∠MND+∠CMN+∠C+∠D=360°,
∵∠CMN=∠A+∠E,∠MND=∠B+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵AD⊥AC,
∴∠CAD=90°,
∵∠BAD=40°,
∴∠BAC=∠CAD+∠BAD=130°,
∵AB∥CD,
∴∠ACD+∠BAC=180°,
∴∠ACD=180°﹣∠BAC=50°.
故答案为:50.
10.解:由题意可得:
地毯的水平长度=BC=12米,地毯的垂直长度=AC=3米,
∴地毯的长度至少需要:12+3=15米,
故答案为:15.
11.解:∵∠A+∠ACB+∠ABC=180°,∠A=90°,
∴∠ACB+∠ABC=90°,
∵∠GCF=∠ACB,∠DBE=∠ABC,
∴∠GCF+∠DBE=90°,
∵∠G+∠F+∠GCF=∠D+∠B+∠DBE=180°,
∴∠G+∠F+∠GCF+∠D+∠B+∠DBE=360°,
∴∠D+∠G+∠AFG+∠AED=270°,
故答案为:270°.
12.解:如图,
根据四边形的内角和可得,∠1+∠2+∠3+∠8=360°,∠4+∠5+∠9+∠10=360°,
∵∠9=∠6+∠7,∠8+∠10=180°,
∴∠1+∠2+∠3+∠8+∠4+∠5+∠10+∠6+∠7=720°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
故答案为:540°.
13.解:∵AB∥CD,
∴∠ABD=∠PDB,
∵∠ABD=∠PCE,
∴∠PDB=∠PCE,
∴BD∥CE,
∴∠CEG=∠DGH,
∵EH平分∠AEC,
∴∠CEH=∠AEH,
∵∠DGH=∠EGF,
∴∠EGF=∠GEF,
∵∠AFD=∠AEG+∠EGF=2∠EGF=86°,
∴∠EGF=43°,
∴∠DGH=43°,
∴∠PCE=∠PDG=∠H+∠DGH=65°,
故答案为:65.
14.解:如图,过点C作CH∥AB,
则∠ABC+∠BCH=180°,
∵∠ABC+∠C+∠CDE=360°,即∠ABC+∠BCH+∠DCH+∠CDE=360°,
∴∠DCH+∠CDE=180°,
∴CH∥DE,
∴AB∥DE,
∴∠DGF=∠1=110°,
∴∠2=180°﹣110°=70°,
故答案为:70°.
15.解:∵AB∥CD,∠CDE=119°,
∴∠AEH=∠CDE=119°,
∵EF平分∠AEH,
∴∠FEH=∠AEH=59.5°,
∵∠DGF=130°,
∴∠FGE=180°﹣∠DGF=50°,
∵∠FEH是△EFG的外角,
∴∠F=∠FEH﹣∠FGE=9.5°.
故答案为:9.5.
16.解:如图,过点A作l1的平行线AC,过点B作l2的平行线BD,
则∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°,
∵∠1=∠2+4°,
∴∠1=17°,
故答案为:17°.
三.解答题(共5小题,满分40分)
17.(1)解:∵DE∥BC(已知),
∴∠C=∠AED(两直线平行,同位角相等).
∵∠A+∠ABC+∠C=180°(三角形内角和定理),
∴∠A=180°﹣∠ABC﹣∠C=180°﹣∠ABC﹣∠AED(等式的性质).
∵∠AED=40°,∠ABC=80°(已知),
∴∠A=180°﹣40°﹣80°=60°(等式的性质);
(2)证明:∵∠BFD+∠DFE=180°(平角定义),
∠BFD+∠CEF=180°(已知),
∴∠DFE=∠CEF(同角的补角相等).
∴DF∥AC(内错角相等,两直线平行).
∴∠EDF=∠AED(两直线平行,内错角相等).
∵DE∥BC(已知),
∴∠AED=∠C(两直线平行,同位角相等).
∴∠EDF=∠C(等量代换).
18.证明:(1)∵∠A=120°,∠ABC=60°,
∴∠A+∠ABC=180°.
∴AD∥BC;
(2)∵AD∥BC,
∴∠1=∠DBC.
∵BD⊥DC,EF⊥DC,
∴∠BDF=90°,∠EFC=90°.
∴∠BDF=∠EFC=90°.
∴BD∥EF.
∴∠2=∠DBC.
∴∠1=∠2.
19.解:∵CE平分∠ACD,∠ACD=140°,
∴∠ACE=×∠ACD=×140°=70°,∠ACB=180°﹣∠ACD=40°,
∵FG∥CE,
∴∠AFG=∠ACE=70°,
∵∠FAG=∠B+∠ACB=85°,
∴∠ADF=180°﹣∠AFG﹣∠FAG=25°.
故∠AGF的度数是25°.
20.解:(1)如图1,过P点作PO∥AB,
∵AB∥CD,
∴CD∥PO∥AB,
∴∠BPO=∠B,∠OPD=∠D,
∵∠BPD=∠BPO+∠OPD,
∴∠BPD=∠B+∠D.
∵∠B=50°,∠D=30°,
∴∠BPD=∠B+∠D=50°+30°=80°;
(2)∠B=∠D+∠BPD,
∵AB∥CD,
∴∠B=∠BOD,
∵∠BOD=∠D+∠BPD,
∴∠B=∠D+∠BPD;
(3)∠BPD=∠B+∠D+∠BQD.
证明:如图3,连接QP并延长,
∵∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQE,
∴∠BPE+DPE=∠B+∠BQE+∠D+∠DQE,即∠BPD=∠B+∠D+∠BQD.
(4)∵∠CMN=∠A+∠E,∠DNB=∠B+∠F,
又∵∠C+∠D+∠CMN+∠DNM=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.
21.解:(1)∠A+∠C+∠APC=360°
如图1所示,过点P作PQ∥AB,
∴∠A+∠APQ=180°,
∵AB∥CD,
∴PQ∥CD,
∴∠C+∠CPQ=180°,
∴∠A+∠APQ+∠C+∠CPQ=360°,即∠A+∠C+∠APC=360°;
(2)∠APC=∠A+∠C,
如图2,作PQ∥AB,
∴∠A=∠APQ,
∵AB∥CD,
∴PQ∥CD,
∴∠C=∠CPQ,
∵∠APC=∠APQ﹣∠CPQ,
∴∠APC=∠A﹣∠C;
(3)由(2)知,∠APC=∠PAB﹣∠PCD,
∵∠APC=30°,∠PAB=140°,
∴∠PCD=110°,
∵AB∥CD,
∴∠PQB=∠PCD=110°,
∵EF∥BC,
∴∠BEF=∠PQB=110°,
∵EF∥BC,
∴∠BEF=∠PQB=110°,
∵∠PEG=∠PEF,
∴∠PEG=∠FEG,
∵EH平分∠BEG,
∴∠GEH=∠BEG,
∴∠PEH=∠PEG﹣∠GEH
=∠FEG﹣∠BEG
=∠BEF
=55°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
