1.5 平方差公式的运用 课件(共23张PPT)
文档属性
| 名称 | 1.5 平方差公式的运用 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 23:59:46 | ||
图片预览







文档简介
(共23张PPT)
2022年春北师大版版数学
七年级下册数学精品课件
1.5 整式的乘法
第一章 整式的乘除
第2课时 平方差公式的运用
七年级数学下(BS)
教学课件
1.掌握平方差公式的结构特征,能运用公式进行简便运算;
2.会用几何图形说明公式的意义,体会数形结合的思想方法.
学习目标
复习导入
1.问:平方差公式是怎样的?
(a+b)(a b)=a2 b2
2.利用平方差公式计算:
(1)(2x+7b)(2x–7b);
(2)(-m+3n)(m+3n).
导入新课
3.你能快速的计算201×199吗?
4x2-49b2
9n2-m2
将长为(a+b),宽为(a-b)的长方形,剪下宽为b的长方形条,拼成有空缺的正方形,你能表示剪拼前后的图形的面积关系吗?
(a+b)(a b) = a2 b2
讲授新课
平方差公式的几何验证
合作探究
一
a
a
b
b
a+b
a-b
b
b
几何验证平方差公式
讲授新课
a
a
b
b
a2 b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2 b2
a-b
a-b
讲授新课
a
a
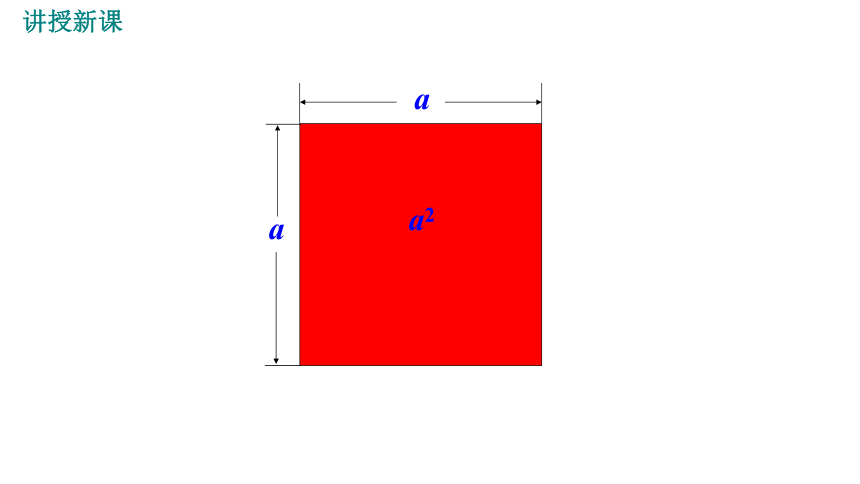
讲授新课
a2
b
a
a
b
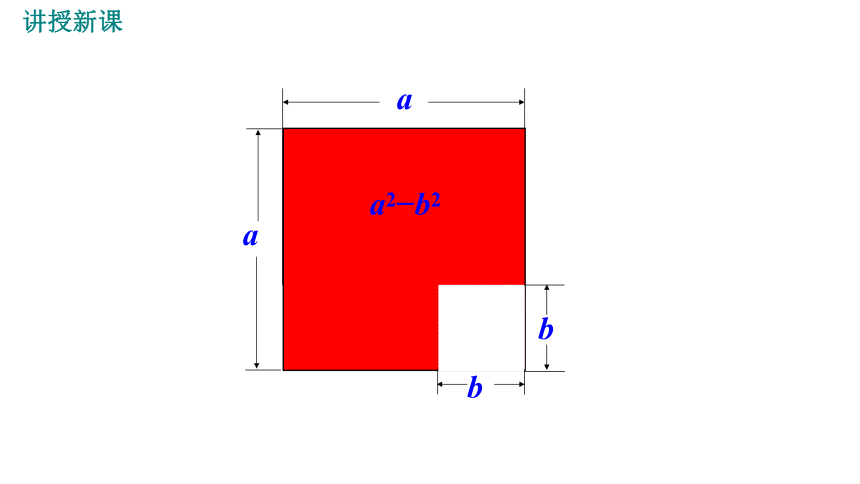
讲授新课
a2 b2
b
a
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
讲授新课
b
a
a
b
(a+b)(a-b)
=
讲授新课
a2 b2
自主探究
想一想:
(1)计算下列各式,并观察他们的共同特点:
6×8=48 14×16=224 69×71=4899
7×7=49 15×15=225 70×70=4900
平方差公式的运用
二
讲授新课
(2)从以上的过程中,你发现了什么规律?请
用字母表示这一规律,你能说明它的正确性吗?
(a+b)(a b)=a2 b2
讲授新课
典例精析
例1 计算:
(1) 103×97; (2) 118×122.
解: 103×97
=(100+3)(100-3)
= 1002-32
=10000 – 9
=9991;
解: 118×122
=(120-2)(120+2)
= 1202-22
=14400-4
=14396.
注意:不能直接应用公式的,要经过变形才可以应用
讲授新课
例2 计算:
(1)a2(a+b)(a-b)+a2b2; (2)(2x-5)(2x+5) –2x(2x-3) .
解:
(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
(2)原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
讲授新课
例3 王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
解:李大妈吃亏了.
理由如下:原正方形的面积为a2,
改变边长后面积为(a+4)(a-4)=a2-16.
∵a2>a2-16,
∴李大妈吃亏了.
讲授新课
当堂练习
1.已知a=7202,b=721×719;则( )
A.a=b B.a>b
C.a2.97×103=( )×( )=( ).
3.(x+6)(x-6)-x(x-9)=0的解是______.
100-3
100+3
1002-32
x=4
B
解:(1)原式=(50+1)(50-1)
=502-12
=2500-1=2499;
(3)原式=(9x2-16)-(6x2+5x-6)
=3x2-5x-10.
(1)51×49;
(3)(3x+4)(3x-4)-(2x+3)(3x-2).
(2)13.2×12.8;
4.利用平方差公式计算:
(2)原式=(13+0.2)×(13-0.2)
=132-0.22
=169-0.04=168.96.
当堂练习
5.计算:
(1) 20162 -2017×2015;
解:20162-2017×2015
=20162-(2016+1)(2016-1)
=20162-(20162-1)
=20162-20162+1
=1;
当堂练习
(2) (y+2) (y-2) – (y-1) (y+5) .
解:(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y + 1.
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
能力拓展:
1.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
当堂练习
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.抓住 “一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
https://www.21cnjy.com/help/help_extract.php
2022年春北师大版版数学
七年级下册数学精品课件
1.5 整式的乘法
第一章 整式的乘除
第2课时 平方差公式的运用
七年级数学下(BS)
教学课件
1.掌握平方差公式的结构特征,能运用公式进行简便运算;
2.会用几何图形说明公式的意义,体会数形结合的思想方法.
学习目标
复习导入
1.问:平方差公式是怎样的?
(a+b)(a b)=a2 b2
2.利用平方差公式计算:
(1)(2x+7b)(2x–7b);
(2)(-m+3n)(m+3n).
导入新课
3.你能快速的计算201×199吗?
4x2-49b2
9n2-m2
将长为(a+b),宽为(a-b)的长方形,剪下宽为b的长方形条,拼成有空缺的正方形,你能表示剪拼前后的图形的面积关系吗?
(a+b)(a b) = a2 b2
讲授新课
平方差公式的几何验证
合作探究
一
a
a
b
b
a+b
a-b
b
b
几何验证平方差公式
讲授新课
a
a
b
b
a2 b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2 b2
a-b
a-b
讲授新课
a
a
讲授新课
a2
b
a
a
b
讲授新课
a2 b2
b
a
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
讲授新课
b
a
a
b
(a+b)(a-b)
=
讲授新课
a2 b2
自主探究
想一想:
(1)计算下列各式,并观察他们的共同特点:
6×8=48 14×16=224 69×71=4899
7×7=49 15×15=225 70×70=4900
平方差公式的运用
二
讲授新课
(2)从以上的过程中,你发现了什么规律?请
用字母表示这一规律,你能说明它的正确性吗?
(a+b)(a b)=a2 b2
讲授新课
典例精析
例1 计算:
(1) 103×97; (2) 118×122.
解: 103×97
=(100+3)(100-3)
= 1002-32
=10000 – 9
=9991;
解: 118×122
=(120-2)(120+2)
= 1202-22
=14400-4
=14396.
注意:不能直接应用公式的,要经过变形才可以应用
讲授新课
例2 计算:
(1)a2(a+b)(a-b)+a2b2; (2)(2x-5)(2x+5) –2x(2x-3) .
解:
(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
(2)原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
讲授新课
例3 王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
解:李大妈吃亏了.
理由如下:原正方形的面积为a2,
改变边长后面积为(a+4)(a-4)=a2-16.
∵a2>a2-16,
∴李大妈吃亏了.
讲授新课
当堂练习
1.已知a=7202,b=721×719;则( )
A.a=b B.a>b
C.a2.97×103=( )×( )=( ).
3.(x+6)(x-6)-x(x-9)=0的解是______.
100-3
100+3
1002-32
x=4
B
解:(1)原式=(50+1)(50-1)
=502-12
=2500-1=2499;
(3)原式=(9x2-16)-(6x2+5x-6)
=3x2-5x-10.
(1)51×49;
(3)(3x+4)(3x-4)-(2x+3)(3x-2).
(2)13.2×12.8;
4.利用平方差公式计算:
(2)原式=(13+0.2)×(13-0.2)
=132-0.22
=169-0.04=168.96.
当堂练习
5.计算:
(1) 20162 -2017×2015;
解:20162-2017×2015
=20162-(2016+1)(2016-1)
=20162-(20162-1)
=20162-20162+1
=1;
当堂练习
(2) (y+2) (y-2) – (y-1) (y+5) .
解:(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y + 1.
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
能力拓展:
1.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
当堂练习
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.抓住 “一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
