湖南省湘一立信实验学校2021-2022学年九年级上学期期末考试数学试题(Word版,含简单答案)
文档属性
| 名称 | 湖南省湘一立信实验学校2021-2022学年九年级上学期期末考试数学试题(Word版,含简单答案) | 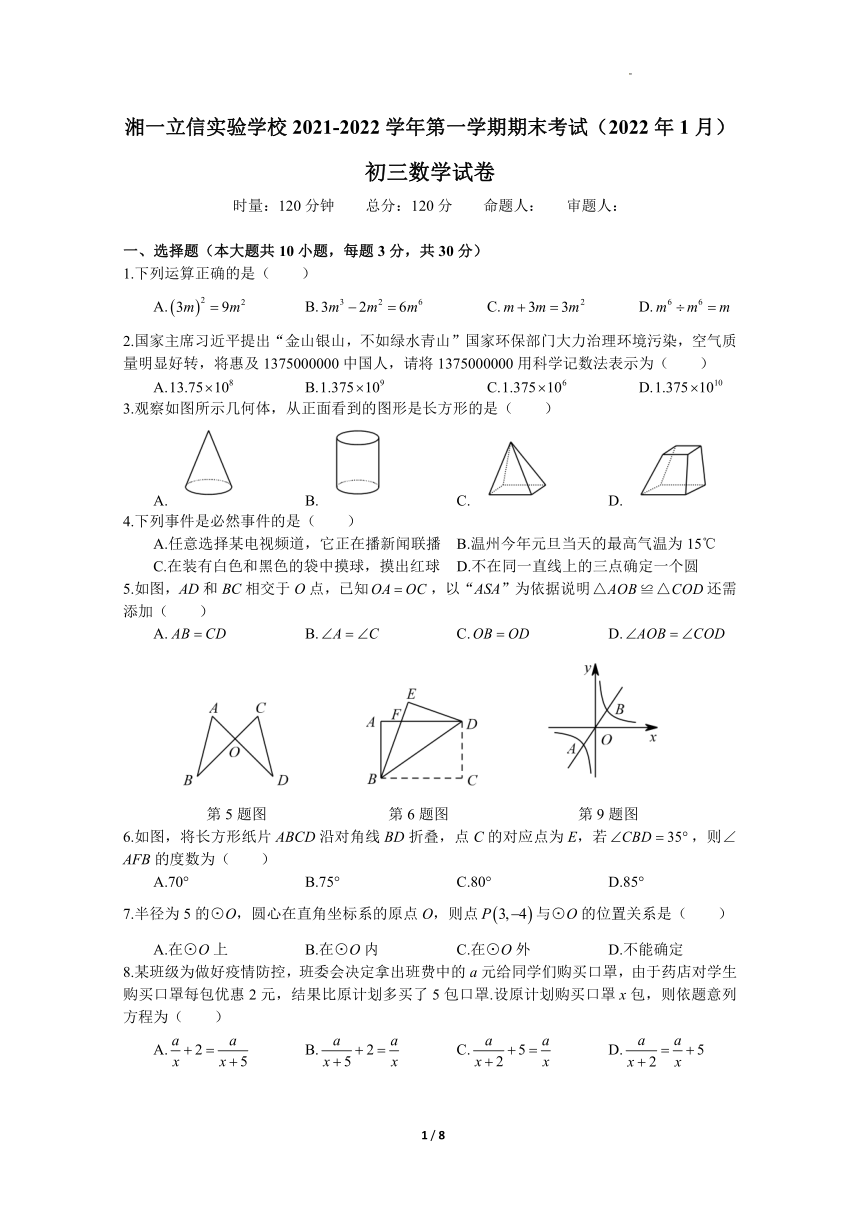 | |
| 格式 | docx | ||
| 文件大小 | 320.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 23:24:11 | ||
图片预览



文档简介
湘一立信实验学校2021-2022学年第一学期期末考试(2022年1月)
初三数学试卷
时量:120分钟 总分:120分 命题人: 审题人:
一、选择题(本大题共10小题,每题3分,共30分)
1.下列运算正确的是( )
A. B. C. D.
2.国家主席习近平提出“金山银山,不如绿水青山”国家环保部门大力治理环境污染,空气质量明显好转,将惠及1375000000中国人,请将1375000000用科学记数法表示为( )
A. B. C. D.
3.观察如图所示几何体,从正面看到的图形是长方形的是( )
A. B. C. D.
4.下列事件是必然事件的是( )
A.任意选择某电视频道,它正在播新闻联播 B.温州今年元旦当天的最高气温为15℃
C.在装有白色和黑色的袋中摸球,摸出红球 D.不在同一直线上的三点确定一个圆
5.如图,AD和BC相交于O点,已知,以“ASA”为依据说明还需添加( )
A. B. C. D.
第5题图 第6题图 第9题图
6.如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为E,若,则∠AFB的度数为( )
A.70° B.75° C.80° D.85°
7.半径为5的⊙O,圆心在直角坐标系的原点O,则点与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
8.某班级为做好疫情防控,班委会决定拿出班费中的a元给同学们购买口罩,由于药店对学生购买口罩每包优惠2元,结果比原计划多买了5包口罩.设原计划购买口罩x包,则依题意列方程为( )
A. B. C. D.
9.如图,反比例函数和正比例函数的图象交于,两点.若,则x的取值范围是( )
A. B.
C.或 D.或
10.如图,正方形ABCD中,E为BC的中点,于G,延长BG交CD于点F,延长CG交BD于点H,交AB于N.下列结论:①;②;③;④;⑤.其中正确结论的个数有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共6小题,每题3分,共18分)
11.因式分解:________.
12.若关于x的一元二次方程有实数根,则k的取值范围是________.
第10题图 第13题图 第15题图
13.一个直角三角形房梁如图所示,其中,,,,垂足为D,那么________.
14.已知菱形的两条对角线长分别为4cm,5cm.则它的面积是________.
15.如图,在Rt△ABC中,,,.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于________.
16.已知抛物线与x轴交于A、B两点,若点A的坐标为,则线段AB的长为________.
三、解答题(共9题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共计72分)
17.计算:.
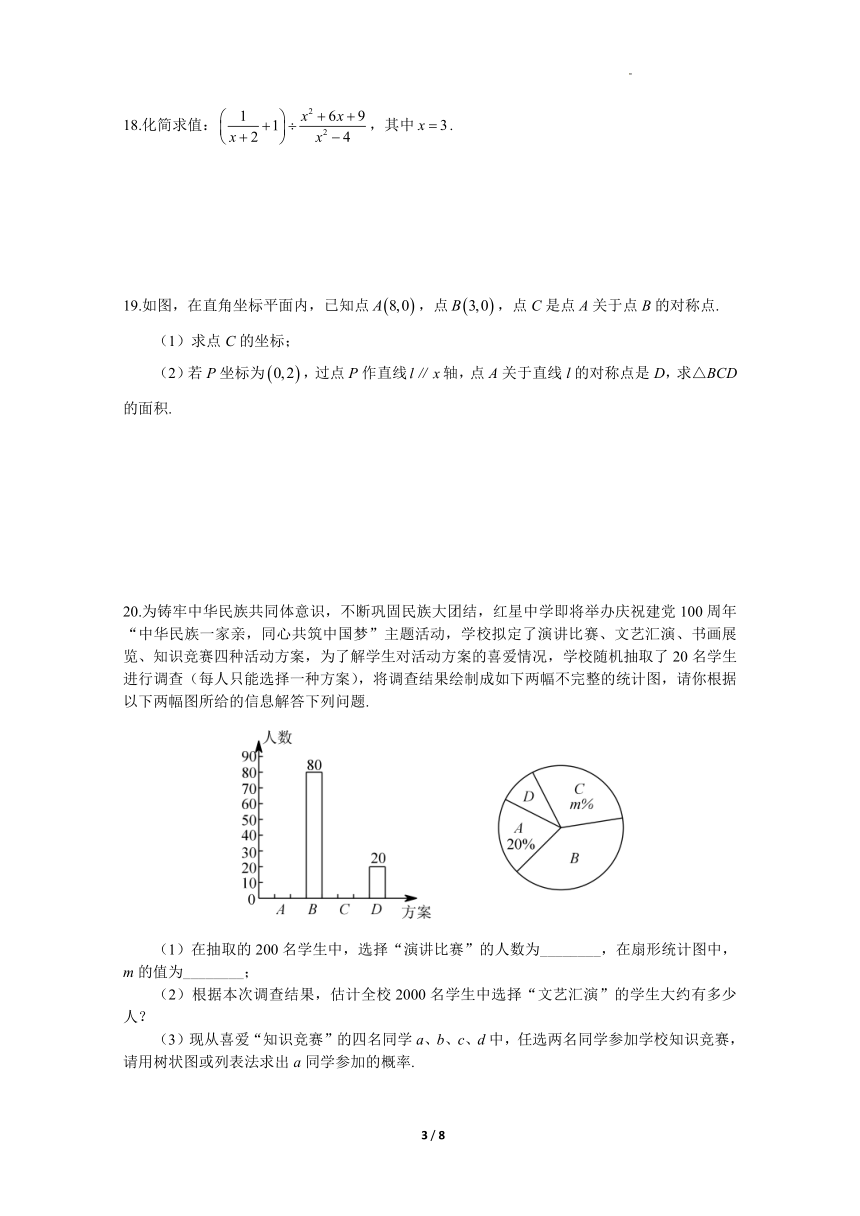
18.化简求值:,其中.
19.如图,在直角坐标平面内,已知点,点,点C是点A关于点B的对称点.
(1)求点C的坐标;
(2)若P坐标为,过点P作直线轴,点A关于直线l的对称点是D,求△BCD的面积.
20.为铸牢中华民族共同体意识,不断巩固民族大团结,红星中学即将举办庆祝建党100周年“中华民族一家亲,同心共筑中国梦”主题活动,学校拟定了演讲比赛、文艺汇演、书画展览、知识竞赛四种活动方案,为了解学生对活动方案的喜爱情况,学校随机抽取了20名学生进行调查(每人只能选择一种方案),将调查结果绘制成如下两幅不完整的统计图,请你根据以下两幅图所给的信息解答下列问题.
(1)在抽取的200名学生中,选择“演讲比赛”的人数为________,在扇形统计图中,m的值为________;
(2)根据本次调查结果,估计全校2000名学生中选择“文艺汇演”的学生大约有多少人?
(3)现从喜爱“知识竞赛”的四名同学a、b、c、d中,任选两名同学参加学校知识竞赛,请用树状图或列表法求出a同学参加的概率.
21.如图,在菱形ABCD中,对角线AC、BD相交于点O,,.
(1)求证:四边形AODE是矩形;
(2)若,,求四边形AODE的面积.
22.学校为了更好地开展“垃圾分类,美丽立信”活动,需购买A,B两种类型垃圾桶,用1600元可购进A型垃圾桶14个和B型垃圾桶8个,且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同,请解答下列问题:
(1)求出A型垃圾桶和B型垃圾桶的单价;
(2)若学校欲用不超过3600元购进两种垃圾桶共50个,其中A型垃圾桶至少29个,求有哪几种购买方案?
23.如图,在Rt△ABC中,,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线;
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,,求的值;
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
24.我们规定,对于已知线段AB,若存在动点C(点C不与点A,B重合)始终满足∠ACB的大小为定值,则称△ABC是“立信三角形”,其中AB的长称为它的“立信长”,∠ACB称为它的“立信角”.
(1)如图(1),已知立信△ABC中“立信长”,“立信角”,请直接写出立信△ABC面积的最大值;
(2)如图(2),在△ABD中,,,C是立信△ABC所在平面上的一个动点,且立信角,求立信△ABC面积的最大值;
(3)如图(3),已知立信长(a是常数且),点C是平面内一动点且满足立信角,若∠ABC,∠BAC的平分线交于点D,问:点D的运动轨迹长度是否为定值?如果是,请求出它的轨迹长度;如果不是,请说明理由.
图1 图2 图3
25.如图,已知抛物线经过,,三点.
(1)求抛物线的解析式;
(2)连接BC,点D是线段BC上方抛物线上一点,过点D作,交x轴于点E,连接AD交BC于点F,当取得最小值时,求点D的横坐标;
(3)点G为抛物线的顶点,抛物线对称轴与x轴交于点H,连接GB,点M是抛物线上的动点,设点M的横坐标为m.
①当时,求点M的坐标;
②过点M作轴,与抛物线交于点N,P为x轴上一点,连接PM,PN,将△PMN沿着MN翻折,得△QMN,若四边形MPNQ恰好为正方形,求m的值.
备用图
2021-2022湘一立信九上期末考试
数学参考答案
一、选择题(共10小题,每小题3分,合计30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B D B A A B C D
二、填空题(共6小题,每小题3分,合计18分)
11. 12.且 13.
14.10 15. 16.8
三、解答题(共9小题,第17、18、19小题每题6分,第20、21小题每题8分,第22、23小题每题9分,第24、25小题每题10分,合计72分)
17.解:原式
18.解:
19.解:(1);(2)
20.解:(1)40人,30;(2)800人;(3)
21.解:(1)略;平行四边形→矩形;(2)
22.解:(1)
;
(2)2种方案 ①A:29 B:21
②A:30 B:20
23.解:(1)略,作垂直证半径
(2)
(3),,,,
24.解:(1);(2);(3)
25.解:(1);
(2)
(3)①or;②ororor 2 / 2
初三数学试卷
时量:120分钟 总分:120分 命题人: 审题人:
一、选择题(本大题共10小题,每题3分,共30分)
1.下列运算正确的是( )
A. B. C. D.
2.国家主席习近平提出“金山银山,不如绿水青山”国家环保部门大力治理环境污染,空气质量明显好转,将惠及1375000000中国人,请将1375000000用科学记数法表示为( )
A. B. C. D.
3.观察如图所示几何体,从正面看到的图形是长方形的是( )
A. B. C. D.
4.下列事件是必然事件的是( )
A.任意选择某电视频道,它正在播新闻联播 B.温州今年元旦当天的最高气温为15℃
C.在装有白色和黑色的袋中摸球,摸出红球 D.不在同一直线上的三点确定一个圆
5.如图,AD和BC相交于O点,已知,以“ASA”为依据说明还需添加( )
A. B. C. D.
第5题图 第6题图 第9题图
6.如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为E,若,则∠AFB的度数为( )
A.70° B.75° C.80° D.85°
7.半径为5的⊙O,圆心在直角坐标系的原点O,则点与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
8.某班级为做好疫情防控,班委会决定拿出班费中的a元给同学们购买口罩,由于药店对学生购买口罩每包优惠2元,结果比原计划多买了5包口罩.设原计划购买口罩x包,则依题意列方程为( )
A. B. C. D.
9.如图,反比例函数和正比例函数的图象交于,两点.若,则x的取值范围是( )
A. B.
C.或 D.或
10.如图,正方形ABCD中,E为BC的中点,于G,延长BG交CD于点F,延长CG交BD于点H,交AB于N.下列结论:①;②;③;④;⑤.其中正确结论的个数有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共6小题,每题3分,共18分)
11.因式分解:________.
12.若关于x的一元二次方程有实数根,则k的取值范围是________.
第10题图 第13题图 第15题图
13.一个直角三角形房梁如图所示,其中,,,,垂足为D,那么________.
14.已知菱形的两条对角线长分别为4cm,5cm.则它的面积是________.
15.如图,在Rt△ABC中,,,.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于________.
16.已知抛物线与x轴交于A、B两点,若点A的坐标为,则线段AB的长为________.
三、解答题(共9题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共计72分)
17.计算:.
18.化简求值:,其中.
19.如图,在直角坐标平面内,已知点,点,点C是点A关于点B的对称点.
(1)求点C的坐标;
(2)若P坐标为,过点P作直线轴,点A关于直线l的对称点是D,求△BCD的面积.
20.为铸牢中华民族共同体意识,不断巩固民族大团结,红星中学即将举办庆祝建党100周年“中华民族一家亲,同心共筑中国梦”主题活动,学校拟定了演讲比赛、文艺汇演、书画展览、知识竞赛四种活动方案,为了解学生对活动方案的喜爱情况,学校随机抽取了20名学生进行调查(每人只能选择一种方案),将调查结果绘制成如下两幅不完整的统计图,请你根据以下两幅图所给的信息解答下列问题.
(1)在抽取的200名学生中,选择“演讲比赛”的人数为________,在扇形统计图中,m的值为________;
(2)根据本次调查结果,估计全校2000名学生中选择“文艺汇演”的学生大约有多少人?
(3)现从喜爱“知识竞赛”的四名同学a、b、c、d中,任选两名同学参加学校知识竞赛,请用树状图或列表法求出a同学参加的概率.
21.如图,在菱形ABCD中,对角线AC、BD相交于点O,,.
(1)求证:四边形AODE是矩形;
(2)若,,求四边形AODE的面积.
22.学校为了更好地开展“垃圾分类,美丽立信”活动,需购买A,B两种类型垃圾桶,用1600元可购进A型垃圾桶14个和B型垃圾桶8个,且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同,请解答下列问题:
(1)求出A型垃圾桶和B型垃圾桶的单价;
(2)若学校欲用不超过3600元购进两种垃圾桶共50个,其中A型垃圾桶至少29个,求有哪几种购买方案?
23.如图,在Rt△ABC中,,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线;
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,,求的值;
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
24.我们规定,对于已知线段AB,若存在动点C(点C不与点A,B重合)始终满足∠ACB的大小为定值,则称△ABC是“立信三角形”,其中AB的长称为它的“立信长”,∠ACB称为它的“立信角”.
(1)如图(1),已知立信△ABC中“立信长”,“立信角”,请直接写出立信△ABC面积的最大值;
(2)如图(2),在△ABD中,,,C是立信△ABC所在平面上的一个动点,且立信角,求立信△ABC面积的最大值;
(3)如图(3),已知立信长(a是常数且),点C是平面内一动点且满足立信角,若∠ABC,∠BAC的平分线交于点D,问:点D的运动轨迹长度是否为定值?如果是,请求出它的轨迹长度;如果不是,请说明理由.
图1 图2 图3
25.如图,已知抛物线经过,,三点.
(1)求抛物线的解析式;
(2)连接BC,点D是线段BC上方抛物线上一点,过点D作,交x轴于点E,连接AD交BC于点F,当取得最小值时,求点D的横坐标;
(3)点G为抛物线的顶点,抛物线对称轴与x轴交于点H,连接GB,点M是抛物线上的动点,设点M的横坐标为m.
①当时,求点M的坐标;
②过点M作轴,与抛物线交于点N,P为x轴上一点,连接PM,PN,将△PMN沿着MN翻折,得△QMN,若四边形MPNQ恰好为正方形,求m的值.
备用图
2021-2022湘一立信九上期末考试
数学参考答案
一、选择题(共10小题,每小题3分,合计30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B D B A A B C D
二、填空题(共6小题,每小题3分,合计18分)
11. 12.且 13.
14.10 15. 16.8
三、解答题(共9小题,第17、18、19小题每题6分,第20、21小题每题8分,第22、23小题每题9分,第24、25小题每题10分,合计72分)
17.解:原式
18.解:
19.解:(1);(2)
20.解:(1)40人,30;(2)800人;(3)
21.解:(1)略;平行四边形→矩形;(2)
22.解:(1)
;
(2)2种方案 ①A:29 B:21
②A:30 B:20
23.解:(1)略,作垂直证半径
(2)
(3),,,,
24.解:(1);(2);(3)
25.解:(1);
(2)
(3)①or;②ororor 2 / 2
同课章节目录
