2013年中考数学复习 第19讲 二次函数
文档属性
| 名称 | 2013年中考数学复习 第19讲 二次函数 |
|
|
| 格式 | zip | ||
| 文件大小 | 476.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-17 00:00:00 | ||
图片预览




文档简介
第19讲 二次函数
本讲重点:二次函数的概念、图像及其性质.
【考点链接】
1.定义:形如的函数叫做二次函数,其图象是 .
2.图象画法:用描点法,先确定顶点、对称轴、开口方向,再对称地描点(一般取 点).
3.抛物线=的对称轴是直线x= ,顶点坐标是(, ).当a>0时,开口向 ,在对称轴左侧,y随x的增大而 ,在对称轴左侧,y随x的增大而 ,x=时,y有最小值 ;当a<0时,开口向下,在对称轴左侧,y随x的增大而增大,在对称轴左侧,y随x的增大而减小,x=时,y有最大值.
4.二次函数的解析式的三种形式:
一般式: (a≠0);
②顶点式: y= (a≠0,其中(m,k)是抛物线的顶点坐标);
③交点式:y= (a≠0,其中x1,x2是一元二次方程的两根).
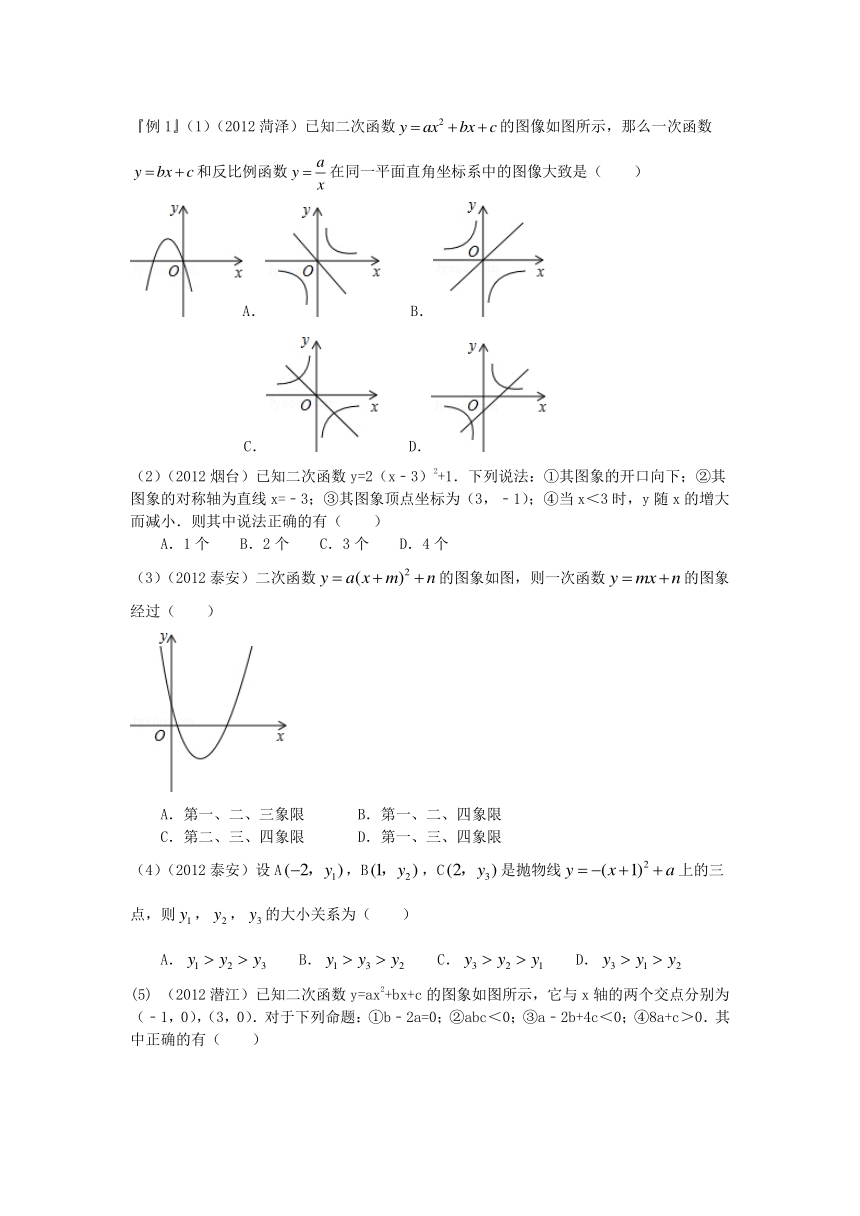
5. 抛物线平移规律是(图中m, k都为正数,a≠0)
【典例探究】
考点1 二次函数的图像和性质
『例1』(1)(2012菏泽)已知二次函数的图像如图所示,那么一次函数和反比例函数在同一平面直角坐标系中的图像大致是( )
A. B.
C. D.
(2)(2012烟台)已知二次函数y=2(x﹣3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=﹣3;③其图象顶点坐标为(3,﹣1);④当x<3时,y随x的增大而减小.则其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
(3)(2012泰安)二次函数的图象如图,则一次函数的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
(4)(2012泰安)设A,B,C是抛物线上的三点,则,,的大小关系为( )
A. B. C. D.
(5) (2012潜江)已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )
A.
3个
B.
2个
C.
1个
D.
0个
『解析』(1)∵二次函数图象开口向下,∴a<0,∵对称轴x=﹣<0,∴b<0,∵二次函数图象经过坐标原点,∴c=0,∴一次函数y=bx+c过第二四象限且经过原点,反比例函数位于第二四象限,纵观各选项,只有C选项符合.
(2)①∵2>0,∴图象的开口向上,故本小题错误;②图象的对称轴为直线x=3,故本小题错误;③其图象顶点坐标为(3,1),故本小题错误;④当x<3时,y随x的增大而减小,正确;综上所述,说法正确的有④共1个.故选A.
(3)∵抛物线的顶点在第四象限,∴﹣m>0,n<0,∴m<0,∴一次函数的图象经过二、三、四象限,故选C.
(4)∵函数的解析式是,如图,∴对称轴是,∴点A关于对称轴的点A′是(0,y1),那么点A′、B、C都在对称轴的右边,而对称轴右边y随x的增大而减小,于是.故选A.
(5) 根据图象可得:a>0,c>0,对称轴:x=﹣>0,①∵它与x轴的两个交点分别为(﹣1,0),(3,0),∴对称轴是x=1,∴﹣=1,∴b+2a=0,故①错误;②∵a>0,
∴b<0,∴abc<0,故②正确;③a﹣2b+4c<0;∵b+2a=0,∴a﹣2b+4c=a+2b﹣4b+4c=﹣4b+4c,∵a﹣b+c=0,∴4a﹣4b+4c=0,∴﹣4b+4c=﹣4a,∵a>0,∴a﹣2b+4c=﹣4b+4c=﹣4a<0,故此选项正确;④根据图示知,当x=4时,y>0,∴16a+4b+c>0,由①知,b=﹣2a,∴8a+c>0,故④正确;故正确为①②③三个.
『备考兵法』公式法和配方法也是求抛物线的顶点坐标和对称轴的两种基本方法.具体选择那种方法要根据题目特征灵活选用.
考点2 求二次函数的解析式
『例2』(1)(2012广州)将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为( )
A.y=x2﹣1 B.y=x2+1 C.y=(x﹣1)2 D.y=(x+1)2
(2)(2011年常州市模拟)已知一个二次函数的图象经过点(0,0),(1,﹣3),(2,﹣8).求这个二次函数的解析式;写出它的对称轴和顶点坐标.
『解析』(1)由“上加下减”的原则可知,将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为:y=x2﹣1.故选A.
(2)已知二次函数的图象经过三个点,常选用一般式来解.设这个二次函数的解析式为,则
解得 ∴这个二次函数的解析式为.
∵=,
∴它的对称轴是直线x=-1,顶点坐标是(-1,1).
『备考兵法』二次函数有三种表示形式,三种表现形式都有三个待定系数,根据不同条件适当选取,可简化计算.一般地,若已知图象上三点用一般式;若已知顶点坐标或对称轴或最值用顶点式;若已知图象与x轴的交点用交点式.
考点3 综合应用
『例3』(2012菏泽)如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.
(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.
『解析』(1)△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,
又A(0,1),B(2,0),O(0,0),∴A′(﹣1,0),B′(0,2).
设抛物线的解析式为:,
∵抛物线经过点A′、B′、B,,解之得,
满足条件的抛物线的解析式为.
(2)∵P为第一象限内抛物线上的一动点,设P(x,y),则x>0,y>0,P点坐标满足.连接PB,PO,PB′,
.
假设四边形的面积是面积的倍,则,
即,解之得,此时,即.
∴存在点P(1,2),使四边形PB′A′B的面积是△A′B′O面积的4倍.
(3)四边形PB′A′B为等腰梯形,答案不唯一,下面性质中的任意2个均可.
①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等.或用符号表示:①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′;②PA′=B′B;③B′P∥A′B;④B′A′=PB.
『备考兵法』本题主要考查代数与几何的综合能力,有一定难度.
【当堂过关】
1. (2012泰安)将抛物线向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A. B.
C. D.
『解析』由“上加下减”的原则可知,将抛物线向上平移3个单位所得抛物线的解析式为:;由“左加右减”的原则可知,将抛物线向左平移2个单位所得抛物线的解析式为.
『答案』A
2. (2012泰安)二次函数的图象如图,若一元二次方程有实数根,则的最大值为( )
A. B.3 C. D.9
『解析』∵抛物线的开口向上,顶点纵坐标为﹣3,∴a>0.,即,
∵一元二次方程有实数根,∴△=,即,即,解得,∴m的最大值为3.
『答案』B
3. (2012湖州)如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
A. B. C.3 D.4
『解析』过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M,∵BF⊥OA,DE⊥OA,CM⊥OA,∴BF∥DE∥CM.∵OD=AD=3,DE⊥OA,∴OE=EA=OA=2.由勾股定理得:DE=.设P(2x,0),根据二次函数的对称性得出OF=PF=x,∵BF∥DE∥CM,∴△OBF∽△ODE,△ACM∽△ADE.∴,即,解得:.∴BF+CM=.
『答案』A
4. (2012?德阳)设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是( )
A. c=3 B. c≥3 C. 1≤c≤3 D. c≤3
『解析』∵当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,∴函数图象过(1,0)点,即1+b+c=0①,
∵当1≤x≤3时,总有y≤0,∴当x=3时,y=9+3b+c≤0②,①②联立解得:c≥3.
『答案』B
5. (2012深圳)二次函数的最小值是 .
『解析』∵,∴当时,函数有最小值5.
『答案』5
6. (2012苏州)已知点A(x1,y1)、B(x2,y2)在二次函数y=(x﹣1)2+1的图象上,若x1>x2>1,则y1 y2(填“>”、“<”或“=”).
『解析』由二次函数y=(x﹣1)2+1可,其对称轴为x=1,∵x1>x2>1,∴两点均在对称轴的右侧,∵此函数图象开口向上,∴在对称轴的右侧y随x的增大而增大,∵x1>x2>1,∴y1>y2.
『答案』>
7. (2012临沂)如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A.O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
解:(1)如图,过B点作BC⊥x轴,垂足为C,则∠BCO=90°,
∵∠AOB=120°,∴∠BOC=60°,又∵OA=OB=4,
∴OC=OB=×4=2,BC=OB?sin60°=4×=2,∴点B的坐标为(﹣2,﹣2);
(2)∵抛物线过原点O和点A.B,∴可设抛物线解析式为y=ax2+bx,
将A(4,0),B(﹣2.﹣2)代入,得,解得,
∴此抛物线的解析式为y=﹣x2+x
(3)存在,如图,抛物线的对称轴是x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),①若OB=OP,则22+|y|2=42,解得y=±2,
当y=2时,在Rt△POD中,∠PDO=90°,sin∠POD==,∴∠POD=60°,
∴∠POB=∠POD+∠AOB=60°+120°=180°,即P、O、B三点在同一直线上,
∴y=2不符合题意,舍去,∴点P的坐标为(2,﹣2)
②若OB=PB,则42+|y+2|2=42,解得y=﹣2,故点P的坐标为(2,﹣2),
③若OP=BP,则22+|y|2=42+|y+2|2,解得y=﹣2,故点P的坐标为(2,﹣2),
综上所述,符合条件的点P只有一个,其坐标为(2,﹣2),
8. (2012烟台)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
解:(1)A(1,4).由题意知,可设抛物线解析式为y=a(x﹣1)2+4
∵抛物线过点C(3,0),∴0=a(3﹣1)2+4,解得,a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3.…(2分)
(2)∵A(1,4),C(3,0),∴可求直线AC的解析式为y=﹣2x+6.
∵点P(1,4﹣t).∴将y=4﹣t代入y=﹣2x+6中,解得点E的横坐标为x=1+.
∴点G的横坐标为1+,代入抛物线的解析式中,可求点G的纵坐标为4﹣.
∴GE=(4﹣)﹣(4﹣t)=t﹣.又点A到GE的距离为,C到GE的距离为2﹣,
即S△ACG=S△AEG+S△CEG=?EG?+?EG(2﹣)=?2(t﹣)=﹣(t﹣2)2+1.
当t=2时,S△ACG的最大值为1.
(3)t=或t=20﹣8.
【浙江两年中考】
1. (2012衢州)已知二次函数y=﹣x2﹣7x+,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2>y3>y1 D.y2<y3<y1
『解析』∵二次函数,∴此函数的对称轴为:.
∵<0<x1<x2<x3,三点都在对称轴右侧,a<0,∴对称轴右侧y随x的增大而减小.∴y1>y2>y3.
『答案』A
2. (2012杭州)已知抛物线与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
A.2 B.3 C.4 D.5
『解析』根据题意,得C(0,﹣3).令y=0,则k(x+1)(x﹣)=0,x=﹣1或x=,
设A点的坐标为(﹣1,0),则B(,0),①当AC=BC时,OA=OB=1,B点的坐标为(1,0),=1,k=3;②当AC=AB时,点B在点A的右面时,∵AC==,则AB=AC=,B点的坐标为(﹣1,0),=﹣1,k=;③当AC=AB时,点B在点A的左面时,B点的坐标为(,0),=,k=;所以能使△ABC为等腰三角形的抛物线的条数是3条.
『答案』B
3. (2012义乌)如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在; ④使得M=1的x值是或.其中正确的是( )
A.①② B.①④ C.②③ D.③④
『解析』①∵当x>0时,利用函数图象可以得出y2>y1.∴此判断错误.②∵抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M.∴当x<0时,根据函数图象可以得出x值越大,M值越大.∴此判断错误.③∵抛物线y1=﹣2x2+2,直线y2=2x+2,与y轴交点坐标为:(0,2),当x=0时,M=2,抛物线y1=﹣2x2+2,最大值为2,故M大于2的x值不存在;∴此判断正确.④ ∵使得M=1时,若y1=﹣2x2+2=1,解得:x1=,x2=﹣;若y2=2x+2=1,解得:x=﹣.由图象可得出:当x=>0,此时对应y1=M.∵抛物线y1=﹣2x2+2与x轴交点坐标为:(1,0),(﹣1,0),∴当﹣1<x<0,此时对应y2=M,∴M=1时,x=或x=﹣.∴此判断正确.因此正确的有③④.
『答案』D
4. (2012杭州)当k分别取﹣1,1,2时,函数y=(k﹣1)x2﹣4x+5﹣k都有最大值吗?请写出你的判断,并说明理由;若有,请求出最大值.
解:∵当开口向下时函数y=(k﹣1)x2﹣4x+5﹣k取最大值,∴k﹣1<0,解得k<1.
∴当k=﹣1时函数y=(k﹣1)x2﹣4x+5﹣k有最大值,当k=1,2时函数没有最大值.
∴当k=﹣1时,函数y=﹣2x2﹣4x+6=﹣2(x+1)2+8.∴最大值为8.
5. (2012丽水)在直角坐标系中,点A是抛物线y=x2在第二象限上的点,连接OA,过点O作OB⊥OA,交抛物线于点B,以OA、OB为边构造矩形AOBC.
(1)如图1,当点A的横坐标为 时,矩形AOBC是正方形;
(2)如图2,当点A的横坐标为时,①求点B的坐标;②将抛物线y=x2作关于x轴的轴对称变换得到抛物线y=-x2,试判断抛物线y=-x2经过平移交换后,能否经过A,B,C三点?如果可以,说出变换的过程;如果不可以,请说明理由.
解:(1) -1.
(2) ①过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
当x=-时,y=(-)2=,即OE=,AE=.
∵∠AOE+∠BOF=180°-90°=90°,21世∠AOE+∠EAO=90°,∴∠EAO=∠BOF.
又∵∠AEO=∠BFO=90°,∴△AEO∽△OFB.∴.
设OF=t,则BF=2t,∴t2=2t,解得:t1=0(舍去),t2=2.∴点B(2,4).
②过点C作CG⊥BF于点G,
∵∠AOE+∠EAO=90°,∠FBO+∠CBG=90°,∠EOA=∠FBO,∴∠EAO=∠CBG.
在△AEO和△BGC中,∠AEO=∠G=900,∠EAO=∠CBG,AO=BC,
∴△AEO≌△BGC(AAS).∴CG=OE=,BG=AE=.
∴xc=2-,yc=4+.∴点C().
∵当x=时,y=-()2+3×+2=,∴点C也在此抛物线上.
∴经过A、B、C三点的抛物线解析式为y=-x2+3x+2=-(x-)2+.
平移方案:先将抛物线y=-x2向右平移个单位,再向上平移个单位得到抛物线
y=-(x-)2+.
【命题趋势提醒】
本节内容二次函数是反映现实世界中变量间的数量关系和变化规律的一种常见的数学模型,是数学中重要内容之一,中考题量约占全部试题的10%~15%,题型既有低档的填空题和选择题,又有中档的解答题,更有大量的综合题.
【迎考精炼】
一、选择题(本大题共10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选,多选,错选均不给分)
1. (2012兰州)抛物线y=-2x2+1的对称轴是( )
A.直线 B. 直线 C. y轴 D. 直线x=2
『解析』∵抛物线y=-2x2+1的顶点坐标为(0,1),∴对称轴是直线x=0(y轴).
『答案』C
2. (2012扬州)将抛物线y=x2+1先向左平移2个单位,再向下平移3个单位,那么所得抛物线的函数关系式是( )
A. y=(x+2)2+2 B. y=(x+2)2-2
C. y=(x-2)2+2 D. y=(x-2)2-2
『解析』将抛物线y=x2+1先向左平移2个单位所得抛物线的函数关系式是:y=(x+2)2+1;将抛物线y=(x+2)2+1先向下平移3个单位所得抛物线的函数关系式是:y=(x+2)2+1-3,即y=(x+2)2-2.
『答案』B
3. (2012德阳)在同一平面直角坐标系内,将函数y=2x2+4x+1的图象沿x轴方向向右平移2个单位长度后再沿y轴向下平移1个单位长度,得到图象的顶点坐标是( )
A.(﹣1,1) B. (1,﹣2) C. (2,﹣2) D. (1,﹣1)
『解析』∵y=2x2+4x+1=2(x2+2x)+1=2[(x+1)2﹣1]+1=2(x+1)2﹣1,∴原抛物线的顶点坐标为(﹣1,﹣1),∵将二次函数y=2(x+1)2﹣1,的图象沿x轴方向向右平移2个单位长度后再沿y轴向下平移1个单位长度,∴y=2(x+1﹣2)2﹣1﹣1=2(x﹣1)2﹣2,
故得到图象的顶点坐标是(1,﹣2).
『答案』B
4. (2012资阳)如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
A.﹣1<x<5 B. x>5
C. x<﹣1且x>5 D. x<﹣1或x>5
『解析』由图象得:对称轴是x=2,其中一个点的坐标为(5,0),∴图象与x轴的另一个交点坐标为(﹣1,0).利用图象可知:ax2+bx+c<0的解集即是y<0的解集,∴x<﹣1或x>5.
『答案』D
5. (2012菏泽)如图为抛物线y=ax2+bx+c的图象,A.B.C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
A.a+b=﹣1 B.a﹣b=﹣1 C.b<2a D.ac<0
『解析』∵OA=OC=1,∴由图象知:C(0,1),A(﹣1,0),把C(0,1)代入得:c=1,把A(﹣1,0)代入得:a﹣b=﹣1.
『答案』B
6. (2012无锡模拟)下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x﹣2)2+1 B.y=(x+2)2+1
C.y=(x﹣2)2﹣3 D.y=(x+2)2﹣3
『解析』∵抛物线对称轴为直线x=2,∴可排除B、D,将点(0,1)代入A中,得
(x﹣2)2+1=(0﹣2)2+1=5,错误,代入C中,得(x﹣2)2﹣3=(0﹣2)2﹣3=1,正确.
『答案』C
7. (2012宿迁模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是2( )
A、a>0 B、当x>1时,y随x的增大而增大
C、c<0 D、3是方程ax2+bx+c=0的一个根
『解析』∵抛物线开口向下,∴a<0,故A选项错误;∵抛物线与y轴的正半轴相交,∴c>0,故B选项错误;∵对称轴x=1,∴当x>1时,y随x的增大而减小;故C选项错误;∵对称轴x=1,∴另一个根为1+2=3,故D选项正确.
『答案』D
8. (2012广安)若二次函数.当≤l时,随的增大而减小,则的取值范围是( )
A.=l B.>l C.≥l D.≤l
『解析』二次函数的开口向上,其对称轴为直线,顶点坐标为,在对称轴的左侧,当时,随的增大而减小.因为当≤l时,随的增大而减小,所以直线应在对称轴直线的左侧或与对称轴重合,则.
『答案』C
9. (2012乐山)二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t值的变化范围是( )
A.0<t<1 B.0<t<2 C.1<t<2 D.﹣1<t<1
『解析』∵二次函数y=ax2+bx+1的顶点在第一象限,且经过点(﹣1,0),∴易得:a﹣b+1=0,a<0,b>0,由a=b﹣1<0得到b<1,结合上面b>0,所以0<b<1①,由b=a+1>0得到a>﹣1,结合上面a<0,所以﹣1<a<0②,∴由①②得:﹣1<a+b<1,且c=1,
得到0<a+b+1<2,∴0<t<2.
『答案』B
10. (2012宜宾)给出定义:设一条直线与一条抛物线只有一个公共点,只这条直线与这条抛物线的对称轴不平行,就称直线与抛物线相切,这条直线是抛物线的切线.有下列命题:
①直线y=0是抛物线y=x2的切线;②直线x=﹣2与抛物线y=x2 相切于点(﹣2,1);③直线y=x+b与抛物线y=x2相切,则相切于点(2,1);④若直线y=kx﹣2与抛物线y=x2 相切,则实数k=.其中正确命题的是( )
A. ①②④ B.①③ C.②③ D.①③④
『解析』①∵直线y=0是x轴,抛物线y=x2的顶点在x轴上,∴直线y=0是抛物线y=x2的切线,故本小题正确;②∵抛物线y=x2的顶点在x轴上,开口向上,直线x=2与y轴平行,∴直线x=﹣2与抛物线y=x2 相交,故本小题错误;③∵直线y=x+b与抛物线y=x2相切,∴x2﹣4x﹣b=0,∴△=16+4b=0,解得b=﹣4,把b=﹣4代入x2﹣4x﹣b=0得x=2,把x=2代入抛物线解析式可知y=1,∴直线y=x+b与抛物线y=x2相切,则相切于点(2,1),故本小题正确;④∵直线y=kx﹣2与抛物线y=x2 相切,∴x2=kx﹣2,即x2﹣kx+2=0,△=k2﹣2=0,解得k=±,故本小题错误.
『答案』B
二、填空题(本大题共6小题,每小题4分,共24分,请将答案填在横线上)
11. (2012淮安模拟)抛物线y=x2-2x-3的顶点坐标是 .
『解析』∵y=x2﹣2x+3=x2﹣2x+1﹣1+3=(x﹣1)2+2,∴抛物线y=x2﹣2x+3的顶点坐标是(1,2).
『答案』(1,2)
12. (2012无锡)若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为 .
『解析』设抛物线的解析式为y=a(x﹣2)2+1,将B(1,0)代入y=a(x﹣2)2+1得,
a=﹣1,函数解析式为y=﹣(x﹣2)2+1,展开得y=﹣x2+4x﹣3.
『答案』y=﹣x2+4x﹣3
13.(2012河池模拟)如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=mx+n(m≠0)的图象,当y2>y1,x的取值范围是 .
『解析』从图象上看出,两个交点坐标分别为(﹣2,0),(1,3),∴当有y2>y1时,有﹣2<x<1.
『答案』﹣2<x<1
14. (2011舟山)如图,已知二次函数y=x2+bx+c的图象经过点(-1,0),(1,-2),当y随x的增大而增大时,x的取值范围是 .
『解析』把(-1,0),(1,-2)代入二次函数y=x2+bx+c中,得
,解得,那么二次函数的解析式是y=x2-x-2.
函数的对称轴是:x=.因而当y随x 的增大而增大时,x的取值范围是:x>.
『答案』x>
15. (2012扬州)如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是 .
『解析』连接DE.设AC=x,则BC=2-x,∵△ACD和△BCE分别是等腰直角三角形,
∴∠DCA=45°,∠ECB=45°,DC=,CE=(2-x),∴∠DCE=90°,
故DE2=DC2+CE2=x2+(2-x)2=x2-2x+2=(x-1)2+1,当x=1时,DE2取得最小值,DE也取得最小值,最小值为1.
『答案』1
16. (2012广安)如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为 .
『解析』过点P作PM⊥y轴于点M,∵抛物线平移后经过原点O和点A(﹣6,0),
∴平移后的抛物线对称轴为x=﹣3,得出二次函数解析式为:y=(x+3)2+h,
将(﹣6,0)代入得出0=(﹣6+3)2+h,解得h=﹣,∴点P的坐标是(3,﹣),
根据抛物线的对称性可知,阴影部分的面积等于矩形NPMO的面积,∴S=3×|﹣|=.
『答案』
三、解答题(本大题共6小题,共46分.解答应写出文字说明、证明过程或演算过程)
17.(6分)(2012桂林模拟)在平面直角坐标系中,将抛物线绕着它与轴的交点旋转180°,求所得抛物线的解析式.
A. B.
C. D.
解:原抛物线解析式可变为y=(x+1)2+2,与轴的交点坐标为(0,3), ∵绕(0,3)旋转180°得到新的抛物线解析式, ∴新的抛物线解析式为:y=-(x-1)2+4.
18.(8分)(2012江西模拟)已知二次函数y=x2+bx﹣2的图象与x轴的一个交点为(1,0),求它与x轴的另一个交点坐标.
解:把x=1,y=0代入y=x2+bx﹣2得:0=1+b﹣2,∴b=1,∴对称轴为,
∴,∴=﹣2,它与x轴的另一个交点坐标是(﹣2,0).
19.(8分)(2012南京模拟)已知函数y=mx2﹣6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
解:(1)当x=0时,y=1.所以不论m为何值,函数y=mx2﹣6x+1的图象都经过y轴上一个定点(0,1);
(2)①当m=0时,函数y=﹣6x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2﹣6x+1的图象与x轴只有一个交点,则方程mx2﹣6x+1=0有两个相等的实数根,所以△=(﹣6)2﹣4m=0,m=9.
综上,若函数y=mx﹣6x+1的图象与x轴只有一个交点,则m的值为0或9.
20.(8分)(2012益阳)已知:如图,抛物线y=a(x﹣1)2+c与x轴交于点A(,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P'作x轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:,,结果可保留根号)
解:(1)∵P与P′(1,3)关于x轴对称,∴P点坐标为(1,﹣3);
∵抛物线y=a(x﹣1)2+c过点A(,0),顶点是P(1,﹣3),
∴;解得;
则抛物线的解析式为y=(x﹣1)2﹣3,即y=x2﹣2x﹣2.
(2)∵CD平行x轴,P′(1,3)在CD上,∴C、D两点纵坐标为3; 由(x﹣1)2﹣3=3,
解得:,,
∴C、D两点的坐标分别为(,3),(,3),∴CD=.
∴“W”图案的高与宽(CD)的比=(或约等于0.6124).
21.(8分)(2012淮安模拟)如图,已知二次函数y= -x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
(1)求此二次函数关系式和点B的坐标;
(2)在x轴的正半轴上是否存在点P,使得△PAB是以AB为底的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)把点A(4,0)代入二次函数有 0=﹣16+4b+3,得b=,
所以二次函数的关系式为y=﹣x2+x+3.当x=0时,y=3, ∴点B的坐标为(0,3).
(2)作AB的垂直平分线交x轴于点P,连接BP,则:BP=AP
设BP=AP=x,则OP=4﹣x,在直角△OBP中,BP2=OB2+OP2
即:x2=32+(4﹣x)2, 解得:x=,∴OP=4﹣=,所以点P的坐标为(,0).
22.(8分)(2012温州)如图,经过原点的抛物线与轴的另一个交点为A.过点作直线轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP.
(1)当时,求点A的坐标及BC的长;
(2)当时,连结CA,问为何值时CA⊥CP?
(3)过点P作PE⊥PC且PE=PC,问是否存在,使得点E落在坐标轴上?若存在,求出所有满足要求的的值,并写出相对应的点E坐标;若不存在,请说明理由.
解:(1)当m=3时,y=-x2+6x.令y=0得-x2+6x=0,解得,x1=0,x2=6.∴A(6,0).
当x=1时,y=5.∴B(1,5).∵抛物线y=-x2+6x的对称轴为直线x=3,且B,C关于对称轴对称,∴BC=4.
(2)过点C作CH⊥x轴于点H(如图1)
由已知得,∠ACP=∠BCH=90°,∴∠ACH=∠PCB.又∵∠AHC=∠PBC=90°,∴△AGH∽△PCB.∴.
∵抛物线y=-x2+2mx的对称轴为直线x=m,其中m>1,且B,C关于对称轴对称,
∴BC=2(m-1).∵B(1,2m-1),P(1,m),∴BP=m-1.
又∵A(2m,0),C(2m-1,2m-1),∴H(2m-1,0).∴AH=1,CH=2m-1,
∴,解得m= .
(3)存在.∵B,C不重合,∴m≠1.
(I)当m>1时,BC=2(m-1),PM=m,BP=m-1,
(i)若点E在x轴上(如图1),
∵∠CPE=90°,∴∠MPE+∠BPC=∠MPE+∠MEP=90°,PC=EP.
∴△BPC≌△MEP,∴BC=PM,即2(m-1)=m,解得m=2.此时点E的坐标是(2,0).
(ii)若点E在y轴上(如图2),过点P作PN⊥y轴于点N,易证△BPC≌△NPE,
∴BP=NP=OM=1,即m-1=1,解得,m=2.此时点E的坐标是(0,4).
(II)当0<m<1时,BC=2(1-m),PM=m,BP=1-m,
(i)若点E在x轴上(如图3),易证△BPC≌△MEP,
∴BC=PM,即2(1-m)=m,解得,m=.此时点E的坐标是( ,0).
(ii)若点E在y轴上(如图4),过点P作PN⊥y轴于点N,易证△BPC≌△NPE,
∴BP=NP=OM=1,即1-m=1,∴m=0(舍去).
综上所述,当m=2时,点E的坐标是(0,2)或(0,4),当m=时,点E的坐标是(,0).
本讲重点:二次函数的概念、图像及其性质.
【考点链接】
1.定义:形如的函数叫做二次函数,其图象是 .
2.图象画法:用描点法,先确定顶点、对称轴、开口方向,再对称地描点(一般取 点).
3.抛物线=的对称轴是直线x= ,顶点坐标是(, ).当a>0时,开口向 ,在对称轴左侧,y随x的增大而 ,在对称轴左侧,y随x的增大而 ,x=时,y有最小值 ;当a<0时,开口向下,在对称轴左侧,y随x的增大而增大,在对称轴左侧,y随x的增大而减小,x=时,y有最大值.
4.二次函数的解析式的三种形式:
一般式: (a≠0);
②顶点式: y= (a≠0,其中(m,k)是抛物线的顶点坐标);
③交点式:y= (a≠0,其中x1,x2是一元二次方程的两根).
5. 抛物线平移规律是(图中m, k都为正数,a≠0)
【典例探究】
考点1 二次函数的图像和性质
『例1』(1)(2012菏泽)已知二次函数的图像如图所示,那么一次函数和反比例函数在同一平面直角坐标系中的图像大致是( )
A. B.
C. D.
(2)(2012烟台)已知二次函数y=2(x﹣3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=﹣3;③其图象顶点坐标为(3,﹣1);④当x<3时,y随x的增大而减小.则其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
(3)(2012泰安)二次函数的图象如图,则一次函数的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
(4)(2012泰安)设A,B,C是抛物线上的三点,则,,的大小关系为( )
A. B. C. D.
(5) (2012潜江)已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )
A.
3个
B.
2个
C.
1个
D.
0个
『解析』(1)∵二次函数图象开口向下,∴a<0,∵对称轴x=﹣<0,∴b<0,∵二次函数图象经过坐标原点,∴c=0,∴一次函数y=bx+c过第二四象限且经过原点,反比例函数位于第二四象限,纵观各选项,只有C选项符合.
(2)①∵2>0,∴图象的开口向上,故本小题错误;②图象的对称轴为直线x=3,故本小题错误;③其图象顶点坐标为(3,1),故本小题错误;④当x<3时,y随x的增大而减小,正确;综上所述,说法正确的有④共1个.故选A.
(3)∵抛物线的顶点在第四象限,∴﹣m>0,n<0,∴m<0,∴一次函数的图象经过二、三、四象限,故选C.
(4)∵函数的解析式是,如图,∴对称轴是,∴点A关于对称轴的点A′是(0,y1),那么点A′、B、C都在对称轴的右边,而对称轴右边y随x的增大而减小,于是.故选A.
(5) 根据图象可得:a>0,c>0,对称轴:x=﹣>0,①∵它与x轴的两个交点分别为(﹣1,0),(3,0),∴对称轴是x=1,∴﹣=1,∴b+2a=0,故①错误;②∵a>0,
∴b<0,∴abc<0,故②正确;③a﹣2b+4c<0;∵b+2a=0,∴a﹣2b+4c=a+2b﹣4b+4c=﹣4b+4c,∵a﹣b+c=0,∴4a﹣4b+4c=0,∴﹣4b+4c=﹣4a,∵a>0,∴a﹣2b+4c=﹣4b+4c=﹣4a<0,故此选项正确;④根据图示知,当x=4时,y>0,∴16a+4b+c>0,由①知,b=﹣2a,∴8a+c>0,故④正确;故正确为①②③三个.
『备考兵法』公式法和配方法也是求抛物线的顶点坐标和对称轴的两种基本方法.具体选择那种方法要根据题目特征灵活选用.
考点2 求二次函数的解析式
『例2』(1)(2012广州)将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为( )
A.y=x2﹣1 B.y=x2+1 C.y=(x﹣1)2 D.y=(x+1)2
(2)(2011年常州市模拟)已知一个二次函数的图象经过点(0,0),(1,﹣3),(2,﹣8).求这个二次函数的解析式;写出它的对称轴和顶点坐标.
『解析』(1)由“上加下减”的原则可知,将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为:y=x2﹣1.故选A.
(2)已知二次函数的图象经过三个点,常选用一般式来解.设这个二次函数的解析式为,则
解得 ∴这个二次函数的解析式为.
∵=,
∴它的对称轴是直线x=-1,顶点坐标是(-1,1).
『备考兵法』二次函数有三种表示形式,三种表现形式都有三个待定系数,根据不同条件适当选取,可简化计算.一般地,若已知图象上三点用一般式;若已知顶点坐标或对称轴或最值用顶点式;若已知图象与x轴的交点用交点式.
考点3 综合应用
『例3』(2012菏泽)如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.
(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.
『解析』(1)△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,
又A(0,1),B(2,0),O(0,0),∴A′(﹣1,0),B′(0,2).
设抛物线的解析式为:,
∵抛物线经过点A′、B′、B,,解之得,
满足条件的抛物线的解析式为.
(2)∵P为第一象限内抛物线上的一动点,设P(x,y),则x>0,y>0,P点坐标满足.连接PB,PO,PB′,
.
假设四边形的面积是面积的倍,则,
即,解之得,此时,即.
∴存在点P(1,2),使四边形PB′A′B的面积是△A′B′O面积的4倍.
(3)四边形PB′A′B为等腰梯形,答案不唯一,下面性质中的任意2个均可.
①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等.或用符号表示:①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′;②PA′=B′B;③B′P∥A′B;④B′A′=PB.
『备考兵法』本题主要考查代数与几何的综合能力,有一定难度.
【当堂过关】
1. (2012泰安)将抛物线向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A. B.
C. D.
『解析』由“上加下减”的原则可知,将抛物线向上平移3个单位所得抛物线的解析式为:;由“左加右减”的原则可知,将抛物线向左平移2个单位所得抛物线的解析式为.
『答案』A
2. (2012泰安)二次函数的图象如图,若一元二次方程有实数根,则的最大值为( )
A. B.3 C. D.9
『解析』∵抛物线的开口向上,顶点纵坐标为﹣3,∴a>0.,即,
∵一元二次方程有实数根,∴△=,即,即,解得,∴m的最大值为3.
『答案』B
3. (2012湖州)如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
A. B. C.3 D.4
『解析』过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M,∵BF⊥OA,DE⊥OA,CM⊥OA,∴BF∥DE∥CM.∵OD=AD=3,DE⊥OA,∴OE=EA=OA=2.由勾股定理得:DE=.设P(2x,0),根据二次函数的对称性得出OF=PF=x,∵BF∥DE∥CM,∴△OBF∽△ODE,△ACM∽△ADE.∴,即,解得:.∴BF+CM=.
『答案』A
4. (2012?德阳)设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是( )
A. c=3 B. c≥3 C. 1≤c≤3 D. c≤3
『解析』∵当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,∴函数图象过(1,0)点,即1+b+c=0①,
∵当1≤x≤3时,总有y≤0,∴当x=3时,y=9+3b+c≤0②,①②联立解得:c≥3.
『答案』B
5. (2012深圳)二次函数的最小值是 .
『解析』∵,∴当时,函数有最小值5.
『答案』5
6. (2012苏州)已知点A(x1,y1)、B(x2,y2)在二次函数y=(x﹣1)2+1的图象上,若x1>x2>1,则y1 y2(填“>”、“<”或“=”).
『解析』由二次函数y=(x﹣1)2+1可,其对称轴为x=1,∵x1>x2>1,∴两点均在对称轴的右侧,∵此函数图象开口向上,∴在对称轴的右侧y随x的增大而增大,∵x1>x2>1,∴y1>y2.
『答案』>
7. (2012临沂)如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A.O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
解:(1)如图,过B点作BC⊥x轴,垂足为C,则∠BCO=90°,
∵∠AOB=120°,∴∠BOC=60°,又∵OA=OB=4,
∴OC=OB=×4=2,BC=OB?sin60°=4×=2,∴点B的坐标为(﹣2,﹣2);
(2)∵抛物线过原点O和点A.B,∴可设抛物线解析式为y=ax2+bx,
将A(4,0),B(﹣2.﹣2)代入,得,解得,
∴此抛物线的解析式为y=﹣x2+x
(3)存在,如图,抛物线的对称轴是x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),①若OB=OP,则22+|y|2=42,解得y=±2,
当y=2时,在Rt△POD中,∠PDO=90°,sin∠POD==,∴∠POD=60°,
∴∠POB=∠POD+∠AOB=60°+120°=180°,即P、O、B三点在同一直线上,
∴y=2不符合题意,舍去,∴点P的坐标为(2,﹣2)
②若OB=PB,则42+|y+2|2=42,解得y=﹣2,故点P的坐标为(2,﹣2),
③若OP=BP,则22+|y|2=42+|y+2|2,解得y=﹣2,故点P的坐标为(2,﹣2),
综上所述,符合条件的点P只有一个,其坐标为(2,﹣2),
8. (2012烟台)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
解:(1)A(1,4).由题意知,可设抛物线解析式为y=a(x﹣1)2+4
∵抛物线过点C(3,0),∴0=a(3﹣1)2+4,解得,a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3.…(2分)
(2)∵A(1,4),C(3,0),∴可求直线AC的解析式为y=﹣2x+6.
∵点P(1,4﹣t).∴将y=4﹣t代入y=﹣2x+6中,解得点E的横坐标为x=1+.
∴点G的横坐标为1+,代入抛物线的解析式中,可求点G的纵坐标为4﹣.
∴GE=(4﹣)﹣(4﹣t)=t﹣.又点A到GE的距离为,C到GE的距离为2﹣,
即S△ACG=S△AEG+S△CEG=?EG?+?EG(2﹣)=?2(t﹣)=﹣(t﹣2)2+1.
当t=2时,S△ACG的最大值为1.
(3)t=或t=20﹣8.
【浙江两年中考】
1. (2012衢州)已知二次函数y=﹣x2﹣7x+,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2>y3>y1 D.y2<y3<y1
『解析』∵二次函数,∴此函数的对称轴为:.
∵<0<x1<x2<x3,三点都在对称轴右侧,a<0,∴对称轴右侧y随x的增大而减小.∴y1>y2>y3.
『答案』A
2. (2012杭州)已知抛物线与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
A.2 B.3 C.4 D.5
『解析』根据题意,得C(0,﹣3).令y=0,则k(x+1)(x﹣)=0,x=﹣1或x=,
设A点的坐标为(﹣1,0),则B(,0),①当AC=BC时,OA=OB=1,B点的坐标为(1,0),=1,k=3;②当AC=AB时,点B在点A的右面时,∵AC==,则AB=AC=,B点的坐标为(﹣1,0),=﹣1,k=;③当AC=AB时,点B在点A的左面时,B点的坐标为(,0),=,k=;所以能使△ABC为等腰三角形的抛物线的条数是3条.
『答案』B
3. (2012义乌)如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在; ④使得M=1的x值是或.其中正确的是( )
A.①② B.①④ C.②③ D.③④
『解析』①∵当x>0时,利用函数图象可以得出y2>y1.∴此判断错误.②∵抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M.∴当x<0时,根据函数图象可以得出x值越大,M值越大.∴此判断错误.③∵抛物线y1=﹣2x2+2,直线y2=2x+2,与y轴交点坐标为:(0,2),当x=0时,M=2,抛物线y1=﹣2x2+2,最大值为2,故M大于2的x值不存在;∴此判断正确.④ ∵使得M=1时,若y1=﹣2x2+2=1,解得:x1=,x2=﹣;若y2=2x+2=1,解得:x=﹣.由图象可得出:当x=>0,此时对应y1=M.∵抛物线y1=﹣2x2+2与x轴交点坐标为:(1,0),(﹣1,0),∴当﹣1<x<0,此时对应y2=M,∴M=1时,x=或x=﹣.∴此判断正确.因此正确的有③④.
『答案』D
4. (2012杭州)当k分别取﹣1,1,2时,函数y=(k﹣1)x2﹣4x+5﹣k都有最大值吗?请写出你的判断,并说明理由;若有,请求出最大值.
解:∵当开口向下时函数y=(k﹣1)x2﹣4x+5﹣k取最大值,∴k﹣1<0,解得k<1.
∴当k=﹣1时函数y=(k﹣1)x2﹣4x+5﹣k有最大值,当k=1,2时函数没有最大值.
∴当k=﹣1时,函数y=﹣2x2﹣4x+6=﹣2(x+1)2+8.∴最大值为8.
5. (2012丽水)在直角坐标系中,点A是抛物线y=x2在第二象限上的点,连接OA,过点O作OB⊥OA,交抛物线于点B,以OA、OB为边构造矩形AOBC.
(1)如图1,当点A的横坐标为 时,矩形AOBC是正方形;
(2)如图2,当点A的横坐标为时,①求点B的坐标;②将抛物线y=x2作关于x轴的轴对称变换得到抛物线y=-x2,试判断抛物线y=-x2经过平移交换后,能否经过A,B,C三点?如果可以,说出变换的过程;如果不可以,请说明理由.
解:(1) -1.
(2) ①过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
当x=-时,y=(-)2=,即OE=,AE=.
∵∠AOE+∠BOF=180°-90°=90°,21世∠AOE+∠EAO=90°,∴∠EAO=∠BOF.
又∵∠AEO=∠BFO=90°,∴△AEO∽△OFB.∴.
设OF=t,则BF=2t,∴t2=2t,解得:t1=0(舍去),t2=2.∴点B(2,4).
②过点C作CG⊥BF于点G,
∵∠AOE+∠EAO=90°,∠FBO+∠CBG=90°,∠EOA=∠FBO,∴∠EAO=∠CBG.
在△AEO和△BGC中,∠AEO=∠G=900,∠EAO=∠CBG,AO=BC,
∴△AEO≌△BGC(AAS).∴CG=OE=,BG=AE=.
∴xc=2-,yc=4+.∴点C().
∵当x=时,y=-()2+3×+2=,∴点C也在此抛物线上.
∴经过A、B、C三点的抛物线解析式为y=-x2+3x+2=-(x-)2+.
平移方案:先将抛物线y=-x2向右平移个单位,再向上平移个单位得到抛物线
y=-(x-)2+.
【命题趋势提醒】
本节内容二次函数是反映现实世界中变量间的数量关系和变化规律的一种常见的数学模型,是数学中重要内容之一,中考题量约占全部试题的10%~15%,题型既有低档的填空题和选择题,又有中档的解答题,更有大量的综合题.
【迎考精炼】
一、选择题(本大题共10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选,多选,错选均不给分)
1. (2012兰州)抛物线y=-2x2+1的对称轴是( )
A.直线 B. 直线 C. y轴 D. 直线x=2
『解析』∵抛物线y=-2x2+1的顶点坐标为(0,1),∴对称轴是直线x=0(y轴).
『答案』C
2. (2012扬州)将抛物线y=x2+1先向左平移2个单位,再向下平移3个单位,那么所得抛物线的函数关系式是( )
A. y=(x+2)2+2 B. y=(x+2)2-2
C. y=(x-2)2+2 D. y=(x-2)2-2
『解析』将抛物线y=x2+1先向左平移2个单位所得抛物线的函数关系式是:y=(x+2)2+1;将抛物线y=(x+2)2+1先向下平移3个单位所得抛物线的函数关系式是:y=(x+2)2+1-3,即y=(x+2)2-2.
『答案』B
3. (2012德阳)在同一平面直角坐标系内,将函数y=2x2+4x+1的图象沿x轴方向向右平移2个单位长度后再沿y轴向下平移1个单位长度,得到图象的顶点坐标是( )
A.(﹣1,1) B. (1,﹣2) C. (2,﹣2) D. (1,﹣1)
『解析』∵y=2x2+4x+1=2(x2+2x)+1=2[(x+1)2﹣1]+1=2(x+1)2﹣1,∴原抛物线的顶点坐标为(﹣1,﹣1),∵将二次函数y=2(x+1)2﹣1,的图象沿x轴方向向右平移2个单位长度后再沿y轴向下平移1个单位长度,∴y=2(x+1﹣2)2﹣1﹣1=2(x﹣1)2﹣2,
故得到图象的顶点坐标是(1,﹣2).
『答案』B
4. (2012资阳)如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
A.﹣1<x<5 B. x>5
C. x<﹣1且x>5 D. x<﹣1或x>5
『解析』由图象得:对称轴是x=2,其中一个点的坐标为(5,0),∴图象与x轴的另一个交点坐标为(﹣1,0).利用图象可知:ax2+bx+c<0的解集即是y<0的解集,∴x<﹣1或x>5.
『答案』D
5. (2012菏泽)如图为抛物线y=ax2+bx+c的图象,A.B.C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
A.a+b=﹣1 B.a﹣b=﹣1 C.b<2a D.ac<0
『解析』∵OA=OC=1,∴由图象知:C(0,1),A(﹣1,0),把C(0,1)代入得:c=1,把A(﹣1,0)代入得:a﹣b=﹣1.
『答案』B
6. (2012无锡模拟)下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x﹣2)2+1 B.y=(x+2)2+1
C.y=(x﹣2)2﹣3 D.y=(x+2)2﹣3
『解析』∵抛物线对称轴为直线x=2,∴可排除B、D,将点(0,1)代入A中,得
(x﹣2)2+1=(0﹣2)2+1=5,错误,代入C中,得(x﹣2)2﹣3=(0﹣2)2﹣3=1,正确.
『答案』C
7. (2012宿迁模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是2( )
A、a>0 B、当x>1时,y随x的增大而增大
C、c<0 D、3是方程ax2+bx+c=0的一个根
『解析』∵抛物线开口向下,∴a<0,故A选项错误;∵抛物线与y轴的正半轴相交,∴c>0,故B选项错误;∵对称轴x=1,∴当x>1时,y随x的增大而减小;故C选项错误;∵对称轴x=1,∴另一个根为1+2=3,故D选项正确.
『答案』D
8. (2012广安)若二次函数.当≤l时,随的增大而减小,则的取值范围是( )
A.=l B.>l C.≥l D.≤l
『解析』二次函数的开口向上,其对称轴为直线,顶点坐标为,在对称轴的左侧,当时,随的增大而减小.因为当≤l时,随的增大而减小,所以直线应在对称轴直线的左侧或与对称轴重合,则.
『答案』C
9. (2012乐山)二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t值的变化范围是( )
A.0<t<1 B.0<t<2 C.1<t<2 D.﹣1<t<1
『解析』∵二次函数y=ax2+bx+1的顶点在第一象限,且经过点(﹣1,0),∴易得:a﹣b+1=0,a<0,b>0,由a=b﹣1<0得到b<1,结合上面b>0,所以0<b<1①,由b=a+1>0得到a>﹣1,结合上面a<0,所以﹣1<a<0②,∴由①②得:﹣1<a+b<1,且c=1,
得到0<a+b+1<2,∴0<t<2.
『答案』B
10. (2012宜宾)给出定义:设一条直线与一条抛物线只有一个公共点,只这条直线与这条抛物线的对称轴不平行,就称直线与抛物线相切,这条直线是抛物线的切线.有下列命题:
①直线y=0是抛物线y=x2的切线;②直线x=﹣2与抛物线y=x2 相切于点(﹣2,1);③直线y=x+b与抛物线y=x2相切,则相切于点(2,1);④若直线y=kx﹣2与抛物线y=x2 相切,则实数k=.其中正确命题的是( )
A. ①②④ B.①③ C.②③ D.①③④
『解析』①∵直线y=0是x轴,抛物线y=x2的顶点在x轴上,∴直线y=0是抛物线y=x2的切线,故本小题正确;②∵抛物线y=x2的顶点在x轴上,开口向上,直线x=2与y轴平行,∴直线x=﹣2与抛物线y=x2 相交,故本小题错误;③∵直线y=x+b与抛物线y=x2相切,∴x2﹣4x﹣b=0,∴△=16+4b=0,解得b=﹣4,把b=﹣4代入x2﹣4x﹣b=0得x=2,把x=2代入抛物线解析式可知y=1,∴直线y=x+b与抛物线y=x2相切,则相切于点(2,1),故本小题正确;④∵直线y=kx﹣2与抛物线y=x2 相切,∴x2=kx﹣2,即x2﹣kx+2=0,△=k2﹣2=0,解得k=±,故本小题错误.
『答案』B
二、填空题(本大题共6小题,每小题4分,共24分,请将答案填在横线上)
11. (2012淮安模拟)抛物线y=x2-2x-3的顶点坐标是 .
『解析』∵y=x2﹣2x+3=x2﹣2x+1﹣1+3=(x﹣1)2+2,∴抛物线y=x2﹣2x+3的顶点坐标是(1,2).
『答案』(1,2)
12. (2012无锡)若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为 .
『解析』设抛物线的解析式为y=a(x﹣2)2+1,将B(1,0)代入y=a(x﹣2)2+1得,
a=﹣1,函数解析式为y=﹣(x﹣2)2+1,展开得y=﹣x2+4x﹣3.
『答案』y=﹣x2+4x﹣3
13.(2012河池模拟)如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=mx+n(m≠0)的图象,当y2>y1,x的取值范围是 .
『解析』从图象上看出,两个交点坐标分别为(﹣2,0),(1,3),∴当有y2>y1时,有﹣2<x<1.
『答案』﹣2<x<1
14. (2011舟山)如图,已知二次函数y=x2+bx+c的图象经过点(-1,0),(1,-2),当y随x的增大而增大时,x的取值范围是 .
『解析』把(-1,0),(1,-2)代入二次函数y=x2+bx+c中,得
,解得,那么二次函数的解析式是y=x2-x-2.
函数的对称轴是:x=.因而当y随x 的增大而增大时,x的取值范围是:x>.
『答案』x>
15. (2012扬州)如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是 .
『解析』连接DE.设AC=x,则BC=2-x,∵△ACD和△BCE分别是等腰直角三角形,
∴∠DCA=45°,∠ECB=45°,DC=,CE=(2-x),∴∠DCE=90°,
故DE2=DC2+CE2=x2+(2-x)2=x2-2x+2=(x-1)2+1,当x=1时,DE2取得最小值,DE也取得最小值,最小值为1.
『答案』1
16. (2012广安)如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为 .
『解析』过点P作PM⊥y轴于点M,∵抛物线平移后经过原点O和点A(﹣6,0),
∴平移后的抛物线对称轴为x=﹣3,得出二次函数解析式为:y=(x+3)2+h,
将(﹣6,0)代入得出0=(﹣6+3)2+h,解得h=﹣,∴点P的坐标是(3,﹣),
根据抛物线的对称性可知,阴影部分的面积等于矩形NPMO的面积,∴S=3×|﹣|=.
『答案』
三、解答题(本大题共6小题,共46分.解答应写出文字说明、证明过程或演算过程)
17.(6分)(2012桂林模拟)在平面直角坐标系中,将抛物线绕着它与轴的交点旋转180°,求所得抛物线的解析式.
A. B.
C. D.
解:原抛物线解析式可变为y=(x+1)2+2,与轴的交点坐标为(0,3), ∵绕(0,3)旋转180°得到新的抛物线解析式, ∴新的抛物线解析式为:y=-(x-1)2+4.
18.(8分)(2012江西模拟)已知二次函数y=x2+bx﹣2的图象与x轴的一个交点为(1,0),求它与x轴的另一个交点坐标.
解:把x=1,y=0代入y=x2+bx﹣2得:0=1+b﹣2,∴b=1,∴对称轴为,
∴,∴=﹣2,它与x轴的另一个交点坐标是(﹣2,0).
19.(8分)(2012南京模拟)已知函数y=mx2﹣6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
解:(1)当x=0时,y=1.所以不论m为何值,函数y=mx2﹣6x+1的图象都经过y轴上一个定点(0,1);
(2)①当m=0时,函数y=﹣6x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2﹣6x+1的图象与x轴只有一个交点,则方程mx2﹣6x+1=0有两个相等的实数根,所以△=(﹣6)2﹣4m=0,m=9.
综上,若函数y=mx﹣6x+1的图象与x轴只有一个交点,则m的值为0或9.
20.(8分)(2012益阳)已知:如图,抛物线y=a(x﹣1)2+c与x轴交于点A(,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P'作x轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:,,结果可保留根号)
解:(1)∵P与P′(1,3)关于x轴对称,∴P点坐标为(1,﹣3);
∵抛物线y=a(x﹣1)2+c过点A(,0),顶点是P(1,﹣3),
∴;解得;
则抛物线的解析式为y=(x﹣1)2﹣3,即y=x2﹣2x﹣2.
(2)∵CD平行x轴,P′(1,3)在CD上,∴C、D两点纵坐标为3; 由(x﹣1)2﹣3=3,
解得:,,
∴C、D两点的坐标分别为(,3),(,3),∴CD=.
∴“W”图案的高与宽(CD)的比=(或约等于0.6124).
21.(8分)(2012淮安模拟)如图,已知二次函数y= -x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
(1)求此二次函数关系式和点B的坐标;
(2)在x轴的正半轴上是否存在点P,使得△PAB是以AB为底的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)把点A(4,0)代入二次函数有 0=﹣16+4b+3,得b=,
所以二次函数的关系式为y=﹣x2+x+3.当x=0时,y=3, ∴点B的坐标为(0,3).
(2)作AB的垂直平分线交x轴于点P,连接BP,则:BP=AP
设BP=AP=x,则OP=4﹣x,在直角△OBP中,BP2=OB2+OP2
即:x2=32+(4﹣x)2, 解得:x=,∴OP=4﹣=,所以点P的坐标为(,0).
22.(8分)(2012温州)如图,经过原点的抛物线与轴的另一个交点为A.过点作直线轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP.
(1)当时,求点A的坐标及BC的长;
(2)当时,连结CA,问为何值时CA⊥CP?
(3)过点P作PE⊥PC且PE=PC,问是否存在,使得点E落在坐标轴上?若存在,求出所有满足要求的的值,并写出相对应的点E坐标;若不存在,请说明理由.
解:(1)当m=3时,y=-x2+6x.令y=0得-x2+6x=0,解得,x1=0,x2=6.∴A(6,0).
当x=1时,y=5.∴B(1,5).∵抛物线y=-x2+6x的对称轴为直线x=3,且B,C关于对称轴对称,∴BC=4.
(2)过点C作CH⊥x轴于点H(如图1)
由已知得,∠ACP=∠BCH=90°,∴∠ACH=∠PCB.又∵∠AHC=∠PBC=90°,∴△AGH∽△PCB.∴.
∵抛物线y=-x2+2mx的对称轴为直线x=m,其中m>1,且B,C关于对称轴对称,
∴BC=2(m-1).∵B(1,2m-1),P(1,m),∴BP=m-1.
又∵A(2m,0),C(2m-1,2m-1),∴H(2m-1,0).∴AH=1,CH=2m-1,
∴,解得m= .
(3)存在.∵B,C不重合,∴m≠1.
(I)当m>1时,BC=2(m-1),PM=m,BP=m-1,
(i)若点E在x轴上(如图1),
∵∠CPE=90°,∴∠MPE+∠BPC=∠MPE+∠MEP=90°,PC=EP.
∴△BPC≌△MEP,∴BC=PM,即2(m-1)=m,解得m=2.此时点E的坐标是(2,0).
(ii)若点E在y轴上(如图2),过点P作PN⊥y轴于点N,易证△BPC≌△NPE,
∴BP=NP=OM=1,即m-1=1,解得,m=2.此时点E的坐标是(0,4).
(II)当0<m<1时,BC=2(1-m),PM=m,BP=1-m,
(i)若点E在x轴上(如图3),易证△BPC≌△MEP,
∴BC=PM,即2(1-m)=m,解得,m=.此时点E的坐标是( ,0).
(ii)若点E在y轴上(如图4),过点P作PN⊥y轴于点N,易证△BPC≌△NPE,
∴BP=NP=OM=1,即1-m=1,∴m=0(舍去).
综上所述,当m=2时,点E的坐标是(0,2)或(0,4),当m=时,点E的坐标是(,0).
同课章节目录
