2021-2022学年高一下学期数学人教A版(2019)必修第二册第六章6.2.5向量的数量积课件(30张ppt)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册第六章6.2.5向量的数量积课件(30张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 20:26:51 | ||
图片预览








文档简介
(共30张PPT)
第6章 平面向量及其应用
6.2.5 向量的数量积
学习目标
XUE XI MU BIAO
1.了解向量数量积的物理背景,即物体在力F的作用下产生位移s所做的功.
2.掌握向量数量积的定义及投影向量.
3.会用两个向量的数量积求两个向量的夹角以及判断两个向量是否垂直.
4.掌握向量数量积的性质
引课:我们已经学习了向量的加、减运算、实数与向量的乘积运算等,知道了它们的几何意义。
总之:向量的加减是:“弯直的变换”,实数与向量的乘积是:“伸缩的变换”,
向量的加法主要是: “首尾相接” ;
向量的减法主要是: “共起点指向被减数的终点”;
实数与向量的乘法主要是:“把原来向量同向或反向缩短或拉伸”。
自然我们会想到一个问题:“向量与向量能不能相乘呢?”,如果能,向量的乘法又该怎样定义呢?
这节课我们开始研究学习《向量的数量积》;
首先我们看一个实例,学习有关的准备知识。
---------------其结果仍是向量。
【实例】力对物体所做的功
θ
功是一个标量,它由力和位移两个向量来确定,这给我们一种启示,能否把功看成两个向量相乘的结果呢?受此启发,我们引入向量“数量积”的概念。
因为力做功计算公式中涉及力与位移的夹角,所以下面我们先要定义向量的夹角的概念。
O
A
B
O
A
B
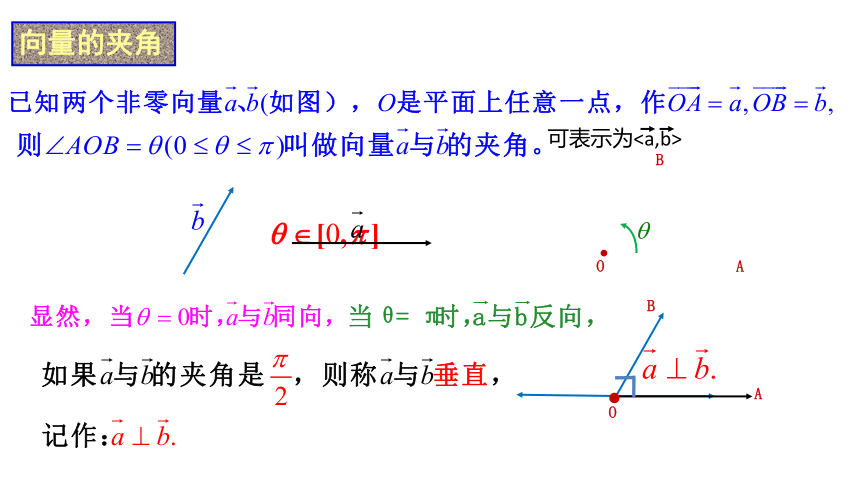
向量的夹角
可表示为
50°
A
B
C
45°
85°
练习一:
在△ABC中,已知A=45°,B=50°,C=85°,求下列向量的夹角:
(1)
45°
130°
85°
45°
130°
85°
(2)
(3)
(3)要注意 =0,但0
(1)向量的线性运算的结果仍是向量,而向量的数量积结果是数量。
【注意】
对比向量的线性运算,我们发现,向量的线性运算的结果是一个向量,而两个向量的数量积是一个数量,这个数量的大小与两个向量的长度及其夹角有关。
平面向量的数量积
【例题解析】
例3 已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|=_____.
由|a|=|2b|=2知,以a与2b为邻边可作出边长为2的菱形OACB,
如图,则|a+2b|= .
如图①,设 和 是两个非零向量,AB= ,CD= ,我们考虑如下的变换:过AB的起点A和终点B,分别作CD所在直线的垂线,垂足分别为A1、B1,得到A1B1,我们称上述变换为向量 向向量 投影,A1B1叫做向量 在向量
上的投影向量.
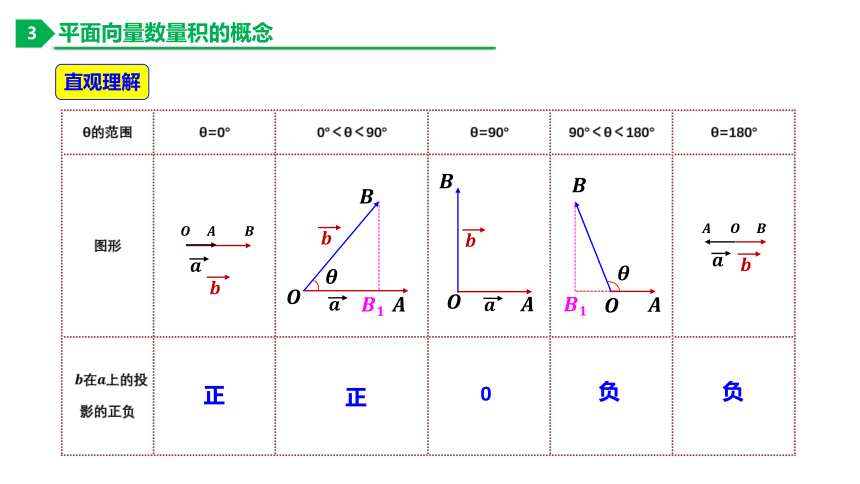
平面向量数量积的概念
3
投影、投影向量
如图②,我们可以在平面内任取一点O,作OM= ,ON= .过点M作直线
ON的垂线,垂足为M1,则OM1就是向量 在向量 上的投影向量.
设与 同方向的单位向量为 , 与 的夹角为θ,则OM1=
平面向量数量积的概念
3
直观理解
正
正
0
负
负
【例题解析】
练习二:
平面向量数量积的性质
设 与 都是非零向量,θ为向量 与 的夹角, 是与 方向相同的单位向量,则有如下性质:
0
;
当且仅当向量共线时,等号成立
既可以证明向量垂直,也可以由垂直进行相关计算
可以用来求向量的模,实现实数运算往向量运算的转化
可用来求两个向量的夹角,夹角的取值与两个向量有关
可以通过向量来证明不等式问题或者求最值问题
向量数量积的运算律
5
向量数量积的三大运算律
和实数的交换律相同
和实数的结合律相同
和实数的分配律相同
已知向量 和实数,向量的数量积满足下列运算律——
【1】,不能得到,如右图.
【2】向量的数量积不满足乘法结合律,不一定等于
.因为表示一个与共线的向量,而式子
表示一个与 共线的向量,它们不一定相同.
例题讲解
【例2】我们知道,对任意a,b∈R,恒有(a+b)2=a2+2ab+b2,(a+b)(a-b)=a2-b2对任意向量,是否也有下面类似的结论?
解:(1)(a+b)2 (2)(a+b)·(a-b)
=(a+b)·(a+b) =a·a-a·b+b·a-b·b
=a·a+a·b+b·a+b·b =a2-b2
=a2+2a·b+b2
√
因为n·(tm+n)=0,
所以t=-4.
3.已知a⊥b,|a|=2,|b|=3,则当k为何值时,向量3a+2b与ka-b互相垂直?
平面向量两两夹角都相等,且
【解】由题意,可得任意两个向量的夹角都是0°或120°
则
当两两夹角为0°时, 方向相同
当两两夹角为120°时, 由于则有
所以
√
两个向量共线分为同向共线与反向共线两种情况,对应的夹角分别是0°和180°,不要弄错.
未弄清向量的夹角而弄错
坑①
已知OA=,OB= ,OC= ,求向量BA与BC的夹角.
显然BA=-2BC,所以BA与BC共线,故它们的夹角为0°.
【错解】 由已知得BA=OA-OB=,
BC=OC-OB= ,
显然BA=-2BC,所以BA与BC共线,
【正解】 由已知得BA=OA-OB=,
BC=OC-OB= ,
因为它们是反向共线,故夹角为180°
平面几何性质运用不准确
坑②
在ΔABC中,|BC|=5,|CA|=6,∠BCA=60°,求BC·CA
【错解】×
【正解】
×
判断两个向量的夹角,应先把两个向量移动到同一起点,BC与CA的夹角是∠BCA的补角.
错用向量运算法则
坑③
已知与的夹角为120°,求和的值.
课堂练习
√
√
√
书面作业
小 结
XIAO JIE
1.知识点:
(1)向量的夹角.
(2)向量数量积的定义.
(3)投影向量.
(4)向量数量积的性质.
2.方法归纳:数形结合.
3.易错点:向量夹角共起点;a·b>0 两向量夹角为锐角,a·b<0 两向量夹角为钝角.
第6章 平面向量及其应用
6.2.5 向量的数量积
学习目标
XUE XI MU BIAO
1.了解向量数量积的物理背景,即物体在力F的作用下产生位移s所做的功.
2.掌握向量数量积的定义及投影向量.
3.会用两个向量的数量积求两个向量的夹角以及判断两个向量是否垂直.
4.掌握向量数量积的性质
引课:我们已经学习了向量的加、减运算、实数与向量的乘积运算等,知道了它们的几何意义。
总之:向量的加减是:“弯直的变换”,实数与向量的乘积是:“伸缩的变换”,
向量的加法主要是: “首尾相接” ;
向量的减法主要是: “共起点指向被减数的终点”;
实数与向量的乘法主要是:“把原来向量同向或反向缩短或拉伸”。
自然我们会想到一个问题:“向量与向量能不能相乘呢?”,如果能,向量的乘法又该怎样定义呢?
这节课我们开始研究学习《向量的数量积》;
首先我们看一个实例,学习有关的准备知识。
---------------其结果仍是向量。
【实例】力对物体所做的功
θ
功是一个标量,它由力和位移两个向量来确定,这给我们一种启示,能否把功看成两个向量相乘的结果呢?受此启发,我们引入向量“数量积”的概念。
因为力做功计算公式中涉及力与位移的夹角,所以下面我们先要定义向量的夹角的概念。
O
A
B
O
A
B
向量的夹角
可表示为
50°
A
B
C
45°
85°
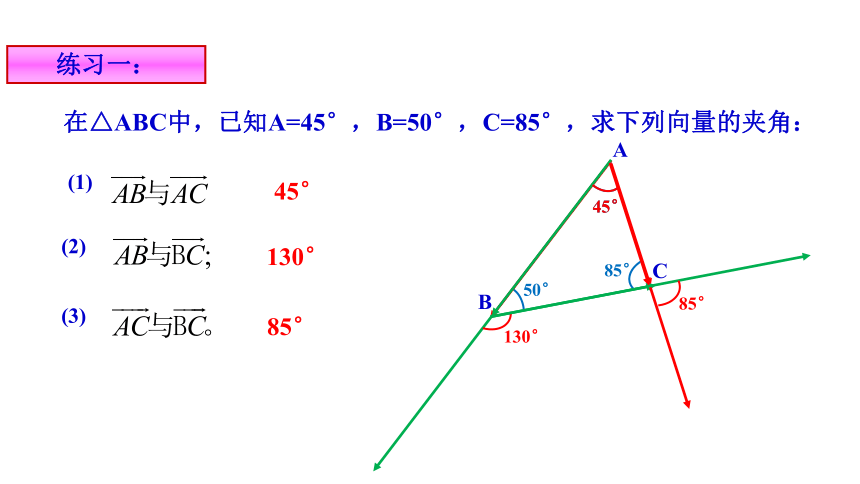
练习一:
在△ABC中,已知A=45°,B=50°,C=85°,求下列向量的夹角:
(1)
45°
130°
85°
45°
130°
85°
(2)
(3)
(3)要注意 =0,但0
(1)向量的线性运算的结果仍是向量,而向量的数量积结果是数量。
【注意】
对比向量的线性运算,我们发现,向量的线性运算的结果是一个向量,而两个向量的数量积是一个数量,这个数量的大小与两个向量的长度及其夹角有关。
平面向量的数量积
【例题解析】
例3 已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|=_____.
由|a|=|2b|=2知,以a与2b为邻边可作出边长为2的菱形OACB,
如图,则|a+2b|= .
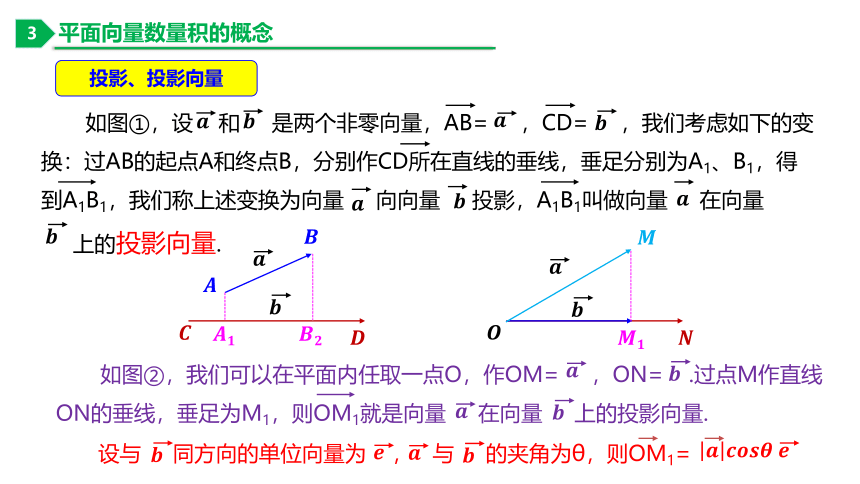
如图①,设 和 是两个非零向量,AB= ,CD= ,我们考虑如下的变换:过AB的起点A和终点B,分别作CD所在直线的垂线,垂足分别为A1、B1,得到A1B1,我们称上述变换为向量 向向量 投影,A1B1叫做向量 在向量
上的投影向量.
平面向量数量积的概念
3
投影、投影向量
如图②,我们可以在平面内任取一点O,作OM= ,ON= .过点M作直线
ON的垂线,垂足为M1,则OM1就是向量 在向量 上的投影向量.
设与 同方向的单位向量为 , 与 的夹角为θ,则OM1=
平面向量数量积的概念
3
直观理解
正
正
0
负
负
【例题解析】
练习二:
平面向量数量积的性质
设 与 都是非零向量,θ为向量 与 的夹角, 是与 方向相同的单位向量,则有如下性质:
0
;
当且仅当向量共线时,等号成立
既可以证明向量垂直,也可以由垂直进行相关计算
可以用来求向量的模,实现实数运算往向量运算的转化
可用来求两个向量的夹角,夹角的取值与两个向量有关
可以通过向量来证明不等式问题或者求最值问题
向量数量积的运算律
5
向量数量积的三大运算律
和实数的交换律相同
和实数的结合律相同
和实数的分配律相同
已知向量 和实数,向量的数量积满足下列运算律——
【1】,不能得到,如右图.
【2】向量的数量积不满足乘法结合律,不一定等于
.因为表示一个与共线的向量,而式子
表示一个与 共线的向量,它们不一定相同.
例题讲解
【例2】我们知道,对任意a,b∈R,恒有(a+b)2=a2+2ab+b2,(a+b)(a-b)=a2-b2对任意向量,是否也有下面类似的结论?
解:(1)(a+b)2 (2)(a+b)·(a-b)
=(a+b)·(a+b) =a·a-a·b+b·a-b·b
=a·a+a·b+b·a+b·b =a2-b2
=a2+2a·b+b2
√
因为n·(tm+n)=0,
所以t=-4.
3.已知a⊥b,|a|=2,|b|=3,则当k为何值时,向量3a+2b与ka-b互相垂直?
平面向量两两夹角都相等,且
【解】由题意,可得任意两个向量的夹角都是0°或120°
则
当两两夹角为0°时, 方向相同
当两两夹角为120°时, 由于则有
所以
√
两个向量共线分为同向共线与反向共线两种情况,对应的夹角分别是0°和180°,不要弄错.
未弄清向量的夹角而弄错
坑①
已知OA=,OB= ,OC= ,求向量BA与BC的夹角.
显然BA=-2BC,所以BA与BC共线,故它们的夹角为0°.
【错解】 由已知得BA=OA-OB=,
BC=OC-OB= ,
显然BA=-2BC,所以BA与BC共线,
【正解】 由已知得BA=OA-OB=,
BC=OC-OB= ,
因为它们是反向共线,故夹角为180°
平面几何性质运用不准确
坑②
在ΔABC中,|BC|=5,|CA|=6,∠BCA=60°,求BC·CA
【错解】×
【正解】
×
判断两个向量的夹角,应先把两个向量移动到同一起点,BC与CA的夹角是∠BCA的补角.
错用向量运算法则
坑③
已知与的夹角为120°,求和的值.
课堂练习
√
√
√
书面作业
小 结
XIAO JIE
1.知识点:
(1)向量的夹角.
(2)向量数量积的定义.
(3)投影向量.
(4)向量数量积的性质.
2.方法归纳:数形结合.
3.易错点:向量夹角共起点;a·b>0 两向量夹角为锐角,a·b<0 两向量夹角为钝角.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
