2021-2022学年北师大版七年级数学下册2.3平行线的性质解答题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册2.3平行线的性质解答题专题训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 299.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 08:49:52 | ||
图片预览
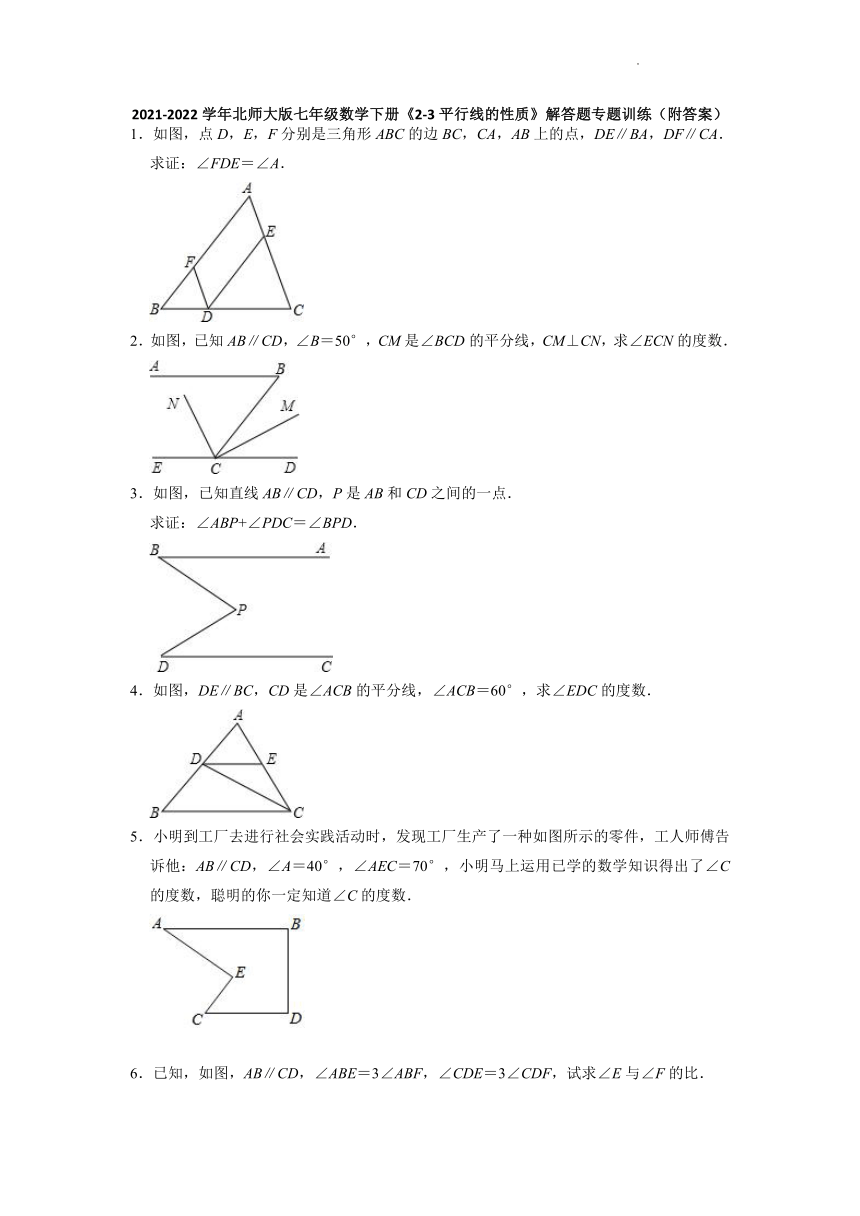



文档简介
2021-2022学年北师大版七年级数学下册《2-3平行线的性质》解答题专题训练(附答案)
1.如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.
求证:∠FDE=∠A.
2.如图,已知AB∥CD,∠B=50°,CM是∠BCD的平分线,CM⊥CN,求∠ECN的度数.
3.如图,已知直线AB∥CD,P是AB和CD之间的一点.
求证:∠ABP+∠PDC=∠BPD.
4.如图,DE∥BC,CD是∠ACB的平分线,∠ACB=60°,求∠EDC的度数.
5.小明到工厂去进行社会实践活动时,发现工厂生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠A=40°,∠AEC=70°,小明马上运用已学的数学知识得出了∠C的度数,聪明的你一定知道∠C的度数.
6.已知,如图,AB∥CD,∠ABE=3∠ABF,∠CDE=3∠CDF,试求∠E与∠F的比.
7.如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,请问∠G等于多少度?写出完整的说理过程.
8.(1)如图AB∥CD,试判断∠BEF、∠EFG、∠FGD之间的关系.并说明理由.
(2)如图AB∥CD,∠AEF=150°,∠DGF=60°.试判断EF和GF的位置关系,并说明理由.
9.如图,已知AB∥CD∥EF,GC⊥CF,∠ABC=65°,∠EFC=40°.求∠BCG的度数.
10.如图所示,直线AB与射线CD平行,点E是AB上的一点,点G是CD上的一点,∠BEF=35°,FC平分∠EFG,若∠C=20°,求∠FGD的度数.
11.已知AD∥BC,AB∥CD,E在线段BC延长线上,AE平分∠BAD.
(1)试证明∠ABC=∠ADC;
(2)若∠ADC=58°,求∠AEC的度数.
12.如图,已知射线AM∥BN,连结AB,点C是射线BN上的一个动点(与点B不重合),AD,AE分别平分∠BAC和∠CAM,交射线BN于点D,E.
(1)试说明:∠ACB=2∠AEB;
(2)若∠ADB﹣∠BAD=45°,求∠AEB的度数.
13.如图,EF∥AD,∠1=∠2.
(1)若∠B=55°,求∠BDG的度数;
(2)若AD平分∠BAC,直接写出∠DGC与∠FEA的数量关系.
14.如图,在三角形ABC中,BF⊥AC,FG∥BC交AB于点G.点H在AB的延长线上,过点H作HE⊥AC交BC于点D,垂足为E.求证:∠1=∠2+∠H.
15.已知一个角的两边与另一个角的两边分别平行,结合图,试探索这两个角之间的关系.
(1)如图1,AB∥EF,BC∥DE.∠1与∠2的关系是: .
(2)如图2,AB∥EF,BC∥DE.∠1与∠2的关系是: .
(3)由(1)(2)你得出的结论是:如果 ,那么 .
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则求这两个角度数.
16.请解答下列问题:
(1)如图1,AB∥CD,试证明:∠B+∠D=∠BED.
(2)已知:如图2,AB∥CD,请直接写出∠BED、∠B、∠D三者之间的关系式.
(3)已知:如图3,AB∥CD,∠ABF=∠DCE.试说明∠BFE与∠FEC的大小关系并说明理由.
17.已知:如图1,直线AB∥CD,EF分别交AB、CD于E、F两点,∠BEF、∠DFE的平分线相交于点K.
(1)求∠EKF的度数.(计算过程不准用三角形内角和)
(2)如图2,∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.
(3)在图2中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,作∠BEKn、∠DFKn的平分线相交于点Kn+1,请用含的n式子表示∠Kn+1的度数.(直接写出答案,不必写解答过程)
18.如图1,AB∥CD,E为直线CD下方一点,BF平分∠ABE.
(1)试说明:∠ABE+∠C﹣∠E=180°.
(2)如图2,EG平分∠BEC,过点B作BH∥GE,当∠FBH=15°时,∠C的度数为 .
(3)如图3,CN平分∠ECD,若BF的反向延长线和CN的反向延长线交于点M,且∠E+∠M=125°,求∠M的度数.
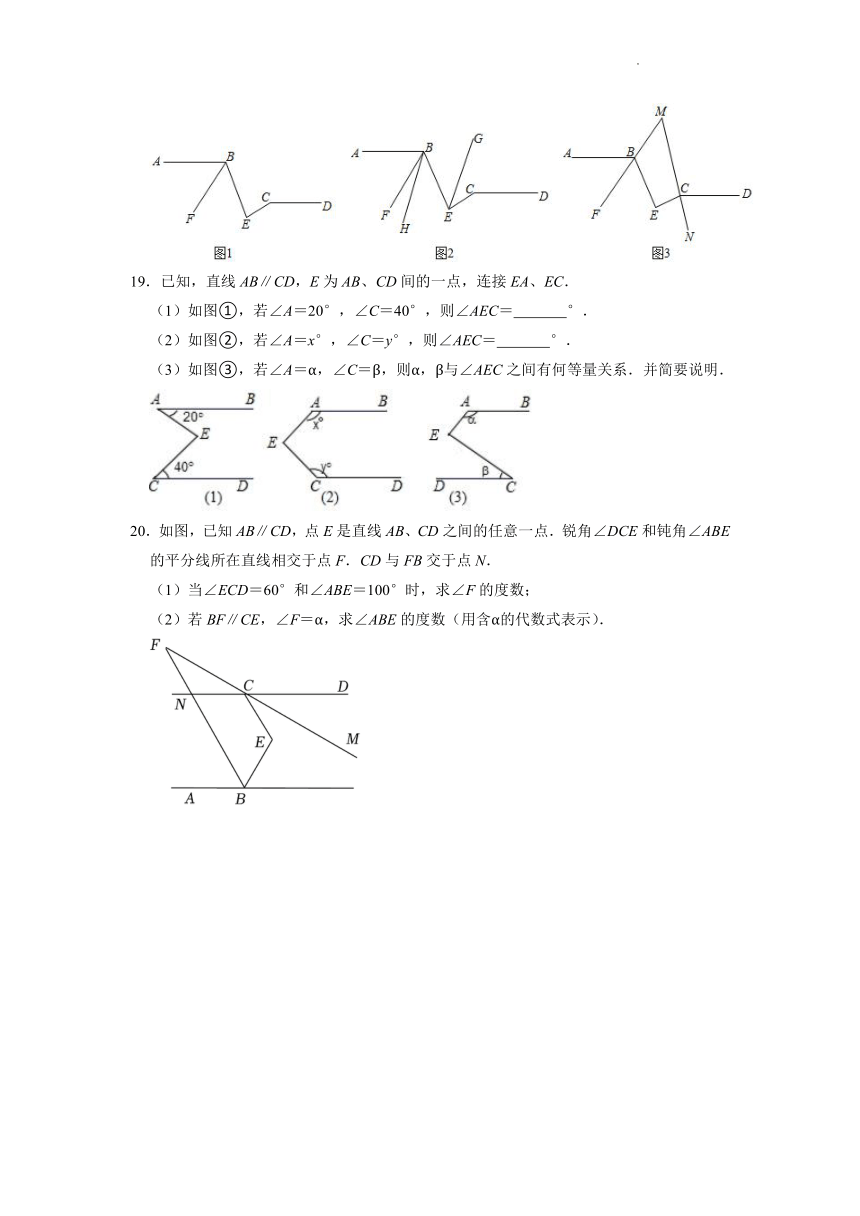
19.已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
(1)如图①,若∠A=20°,∠C=40°,则∠AEC= °.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC= °.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
20.如图,已知AB∥CD,点E是直线AB、CD之间的任意一点.锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F.CD与FB交于点N.
(1)当∠ECD=60°和∠ABE=100°时,求∠F的度数;
(2)若BF∥CE,∠F=α,求∠ABE的度数(用含α的代数式表示).
参考答案
1.证明:∵DE∥BA,
∴∠FDE=∠BFD;
∵DF∥CA,
∴∠A=∠BFD,
∴∠FDE=∠A.
2.解:∵AB∥CD,∠B=50°,
∴∠BCD=∠B=50°,
∵CM平分∠BCD,
∴∠MCD=∠BCD=25°,
∵CM⊥CN,
∴∠MCN=90°,
∴∠ECN=180°﹣90°﹣25°=65°.
3.证明:过点P作PE∥AB,
∵直线AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠1+∠2=∠B+∠D,
即∠ABP+∠PDC=∠BPD.
4.解:∵CD是∠ACB的平分线,∠ACB=60°,
∴∠DCB=30°,
∵DE∥BC,
∴∠EDC=∠DCB=30°.
5.解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠FEA=∠A=40°,∠C=∠FEC,
∵∠AEC=70°,
∴∠FEC=∠AEC﹣∠FEA=70°﹣40°=30°.
∴∠C=30°.
故答案为:30°.
6.解:过点E、F分别作AB的平行线EG、FH,由平行线的传递性可得AB∥EG∥FH∥CD,
∵AB∥FH,
∴∠ABF=∠BFH,
∵FH∥CD,
∴∠CDF=∠DFH,
∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF;
同理可得∠BED=∠DEG+∠BEG=∠ABE+∠CDE;
∵3∠ABF=∠ABE,3∠CDF=∠CDE,
∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF=(∠ABE+∠CDE)=∠BED,
∴∠BED:∠BFD=3:1.
7.解:∵AB∥CD,
∴∠BEF+∠DFE=180°,
又∵EG平分∠BEF,FG平分∠DFE,
∴∠1=∠BEF,∠2=∠DFE,
∴∠1+∠2=(∠BEF+∠DFE)=×180°=90°,
∴∠EGF=180°﹣(∠1+∠2)=180°﹣90°=90°.
8.(1)解:∠EFG=∠FGD+∠BEF
证明:过点F作AB的平行线FH
∵AB∥CD,AB∥FH
∴CD∥FH(平行于同一条直线的两条直线互相平行)
∵AB∥FH(已作)
∴∠BEF=∠EFH(两直线平行,内错角相等)
∵CD∥FH(已证)
∴∠FGD=∠HFG(两直线平行,内错角相等
∴∠BEF+∠FGD=∠EFH+∠HFG(等量代换)
即:∠BEF+∠FGD=∠EFG
∴∠EFG=∠FGD+∠BEF
(2)EF⊥FG
证明:过点F作AB的平行线FH
∵AB∥CD,AB∥FH
∴CD∥FH(平行于同一条直线的两条直线互相平行)
∵∠AEF+∠BEF=180°(平角的定义)
∴∠BEF=180°﹣∠AEF=180°﹣150°=30°
∵AB∥FH(已作)
∴∠BEF=∠EFH(两直线平行,内错角相等)
∵CD∥FH(已证)
∴∠FGD=∠HFG(两直线平行,内错角相等)
∴∠BE+∠FGD=∠EFH+∠HFG(等量代换)
即:∠BEF+∠FGD=∠EFG
∴∠EFG=∠FGD+∠BEF=60°+30°=90°
∴EF⊥FG(垂直的定义)
9.解:∵AB∥CD∥EF,∠B=60°,∠EFC=45°,
∴∠ABC=∠BCD=60°,∠DCF=∠EFC=45°,
∴∠BCF=105°,
∵GC⊥CF,
∴∠GCF=90°,
∴∠BCG的度数为:105°﹣90°=15°.
10.解:如图,过点F作FH∥AB,
∵AB∥CD,
∴AB∥FH∥CD,
∴∠EFH=∠BEF=35°,∠CFH=∠C=20°,
∴∠CFE=∠EFH+∠CFH=35°+20°=55°,
∵FC平分∠EFG,
∴∠CFG=∠CFE=55°,
∴∠GFH=∠CFG+∠CFH=55°+20°=75°,
∵FH∥CD,
∴∠FGD=∠GFH=75°.
11.(1)证明:∵AB∥CD,
∴∠ABC=∠DCE,
∵AD∥BC,
∴∠ADC=∠DCE,
∴∠ABC=∠ADC,
(2)解:∵AB∥CD,
∴∠BAD=180°﹣∠ADC=180°﹣58°=122°,
∵AE平分∠BAD,
∴,
∵AD∥BC,
∴∠AEC=∠DAE=61°.
12.解:(1)∵AE分别平分∠CAM,
∴∠CAM=2∠EAM.
∵AM∥BN,
∴∠CAM=∠ACB,∠EAM=∠AEB.
∴∠ACB=2∠AEB.
(2)∵AM∥BN,
∴∠CAM=∠ACB,∠ADB=∠DAM.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵∠ADB﹣∠BAD=45°,
∴∠DAM﹣∠CAD=45°.
∴∠CAM=∠ACB=45°.
由(1)知∠ACB=2∠AEB,
∴∠AEB=22.5°.
13.解:(1)∵EF∥AD,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴DG∥BA,
∴∠B+∠BDG=180°,
∵∠B=55°,
∴∠BDG=125°;
(2)∠DGC+∠FEA=180°,
理由:∵AD平分∠BAC,
∴∠BAC=2∠3,
由(1)知,DG∥BA,
∴∠CGD=∠BAC,
∴∠CGD=2∠3,
∵EF∥AD,
∴∠FEA+∠3=180°,
∴∠DGC+∠FEA=180°.
14.证明:∵BF⊥AC,HE⊥AC,
∴BF∥EH.
∴∠H=∠ABF,∠2=∠FBC.
∵FG∥BC,
∴∠1=∠ABC.
∵∠ABC=∠ABF+∠FBC,
∴∠1=∠2+∠H.
15.解:(1)∠1=∠2.
理由:如图1,
∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2;
故答案为:∠1=∠2;
(2)∠1+∠2=180°,
理由:如图2,
∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°;
故答案为:∠1+∠2=180°;
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故答案为:一个角的两边与另一个角的两边分别平行,这两个角相等或互补;
(4)设另一个角为x°,根据以上结论得:
2x﹣30=x或2x﹣30+x=180°,
解得:x=30,或x=70,
这两个角度数为:30°、30°或110°,70°.
16.解:(1)证明:作EF∥AB,则EF∥AB∥CD,
∴∠1=∠B,∠2=∠D,
∴∠1+∠2=∠B+∠D,
即∠B+∠D=∠BED;
(2)∠BED+∠B+∠D=360°
证明:作EF∥AB,则EF∥AB∥CD,
∴∠1+∠B=180°,∠2+∠D=180°,
∴∠1+∠B+∠2+∠D=360°,
即∠BED+∠B+∠D=360°;
(3)∠BFE=∠FEC,
证明:作EG∥CD.
根据(1)可以得到∠BFE=∠B+∠FEG,
∵EG∥CD,
∴∠GEC=∠C,
又∵∠FEC=∠FEG+∠GEC,
∴∠FEC=∠BFE.
17.
解:(1)过K作KG∥AB,可得KG∥CD,
∴∠BEK=∠EKG,∠GKF=∠KFD,
∵EK、FK分别为∠BEF与∠EFD的平分线,
∴∠BEK=∠FEK,∠EFK=∠DFK,
∵AB∥CD,
∴∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠DFK)=180°,
∴∠BEK+∠DFK=90°,
则∠EKF=∠EKG+∠GKF=90°;
(2)∠K=2∠K1,理由为:
∵∠BEK、∠DFK的平分线相交于点K1,
∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,
∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,
∴∠BEK+∠KFD=90°,即∠KEK1+∠KFK1=45°,
∴∠K1=180°﹣(∠KEF+∠EFK)﹣(∠KEK1+∠KFK1)=45°,
则∠K=2∠K1;
(3)归纳总结得:∠Kn+1=×90°.
18.(1)证明:过点E作EK∥AB,如图1所示
∴∠ABE=∠BEK,
∵AB∥CD,
∴EK∥CD,
∴∠CEK+∠C=180°
∴∠ABE+∠C﹣∠BEC=∠BEC+∠CEK+∠C﹣∠BEC=∠CEK+∠C=180°;
(2)解:∵BF、EG分别平分∠ABE、∠BEC,
∴∠ABF=∠EBF,∠BEG=∠CEG,
设∠ABF=∠EBF=α,∠BEG=∠CEG=β,
∵BH∥EG,
∴∠HBE=∠BEG=β,
∴∠FBH=∠FBE﹣∠HBE=α﹣β,
由(1)知,∠ABE+∠C﹣∠BEC=180°,
即2α+∠C﹣2β=2(α﹣β)+∠C=180°,
∴2∠FBH+∠C=180°;
∵∠FBH=15°,
∴∠C=180°﹣2∠FBH=180°﹣2×15°=150°.
故答案为150°;
(3)解:∵CN、BF分别平分∠ECD、∠ABE,
∴∠ABF=∠EBF,∠ECN=∠DCN,
设∠ABF=∠EBF=x,∠ECN=∠DCN=y,
由(1)知:∠ABE+∠C﹣∠E=180°,
即∠E=2(x+y)﹣180°,
过M作PQ∥AB,
∵AB∥CD,
∴PQ∥CD,
则∠PMF=∠ABF=x,∠QMN=∠DCN=y,
∴∠FMN=180°﹣∠PMF﹣∠QMN=180°﹣(x+y),
∴∠E+∠FMN=x+y,
∵∠E+∠FMN=125°,
∴x+y=125°,
∴∠FMN=180°﹣(x+y)=180°﹣125°=55°.
19.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF.
(1)∵∠A=20°,∠C=40°,
∴∠1=∠A=20°,∠2=∠C=40°,
∴∠AEC=∠1+∠2=60°;
(2)∴∠1+∠A=180°,∠2+∠C=180°,
∵∠A=x°,∠C=y°,
∴∠1+∠2+x°+y°=360°,
∴∠AEC=360°﹣x°﹣y°;
(3)∠A=α,∠C=β,
∴∠1+∠A=180°,∠2=∠C=β,
∴∠1=180°﹣∠A=180°﹣α,
∴∠AEC=∠1+∠2=180°﹣α+β.
20.解:如图,过点F作FH//CD,
∵锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F,∠ECD=60°,∠ABE=100°,
∴∠DCM=∠ECM=30°,∠ABN=∠EBN=50°°,
∴∠NCF=30°,
∵AB∥CD,FH//CD,
∴FH∥AB,
∴∠HFB=∠ABN=50°,∠HFC=∠FCN=30°,
∴∠BFC=20°.
(2)如图,
∵BF∥CE,
∴∠ECM=∠BFM=α,
∴∠DCE=∠DNB=2α,
∵AB∥CD
∴∠ABN=∠BNC=2α,
∴∠ABE=4α.
1.如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.
求证:∠FDE=∠A.
2.如图,已知AB∥CD,∠B=50°,CM是∠BCD的平分线,CM⊥CN,求∠ECN的度数.
3.如图,已知直线AB∥CD,P是AB和CD之间的一点.
求证:∠ABP+∠PDC=∠BPD.
4.如图,DE∥BC,CD是∠ACB的平分线,∠ACB=60°,求∠EDC的度数.
5.小明到工厂去进行社会实践活动时,发现工厂生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠A=40°,∠AEC=70°,小明马上运用已学的数学知识得出了∠C的度数,聪明的你一定知道∠C的度数.
6.已知,如图,AB∥CD,∠ABE=3∠ABF,∠CDE=3∠CDF,试求∠E与∠F的比.
7.如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,请问∠G等于多少度?写出完整的说理过程.
8.(1)如图AB∥CD,试判断∠BEF、∠EFG、∠FGD之间的关系.并说明理由.
(2)如图AB∥CD,∠AEF=150°,∠DGF=60°.试判断EF和GF的位置关系,并说明理由.
9.如图,已知AB∥CD∥EF,GC⊥CF,∠ABC=65°,∠EFC=40°.求∠BCG的度数.
10.如图所示,直线AB与射线CD平行,点E是AB上的一点,点G是CD上的一点,∠BEF=35°,FC平分∠EFG,若∠C=20°,求∠FGD的度数.
11.已知AD∥BC,AB∥CD,E在线段BC延长线上,AE平分∠BAD.
(1)试证明∠ABC=∠ADC;
(2)若∠ADC=58°,求∠AEC的度数.
12.如图,已知射线AM∥BN,连结AB,点C是射线BN上的一个动点(与点B不重合),AD,AE分别平分∠BAC和∠CAM,交射线BN于点D,E.
(1)试说明:∠ACB=2∠AEB;
(2)若∠ADB﹣∠BAD=45°,求∠AEB的度数.
13.如图,EF∥AD,∠1=∠2.
(1)若∠B=55°,求∠BDG的度数;
(2)若AD平分∠BAC,直接写出∠DGC与∠FEA的数量关系.
14.如图,在三角形ABC中,BF⊥AC,FG∥BC交AB于点G.点H在AB的延长线上,过点H作HE⊥AC交BC于点D,垂足为E.求证:∠1=∠2+∠H.
15.已知一个角的两边与另一个角的两边分别平行,结合图,试探索这两个角之间的关系.
(1)如图1,AB∥EF,BC∥DE.∠1与∠2的关系是: .
(2)如图2,AB∥EF,BC∥DE.∠1与∠2的关系是: .
(3)由(1)(2)你得出的结论是:如果 ,那么 .
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则求这两个角度数.
16.请解答下列问题:
(1)如图1,AB∥CD,试证明:∠B+∠D=∠BED.
(2)已知:如图2,AB∥CD,请直接写出∠BED、∠B、∠D三者之间的关系式.
(3)已知:如图3,AB∥CD,∠ABF=∠DCE.试说明∠BFE与∠FEC的大小关系并说明理由.
17.已知:如图1,直线AB∥CD,EF分别交AB、CD于E、F两点,∠BEF、∠DFE的平分线相交于点K.
(1)求∠EKF的度数.(计算过程不准用三角形内角和)
(2)如图2,∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.
(3)在图2中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,作∠BEKn、∠DFKn的平分线相交于点Kn+1,请用含的n式子表示∠Kn+1的度数.(直接写出答案,不必写解答过程)
18.如图1,AB∥CD,E为直线CD下方一点,BF平分∠ABE.
(1)试说明:∠ABE+∠C﹣∠E=180°.
(2)如图2,EG平分∠BEC,过点B作BH∥GE,当∠FBH=15°时,∠C的度数为 .
(3)如图3,CN平分∠ECD,若BF的反向延长线和CN的反向延长线交于点M,且∠E+∠M=125°,求∠M的度数.
19.已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
(1)如图①,若∠A=20°,∠C=40°,则∠AEC= °.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC= °.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
20.如图,已知AB∥CD,点E是直线AB、CD之间的任意一点.锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F.CD与FB交于点N.
(1)当∠ECD=60°和∠ABE=100°时,求∠F的度数;
(2)若BF∥CE,∠F=α,求∠ABE的度数(用含α的代数式表示).
参考答案
1.证明:∵DE∥BA,
∴∠FDE=∠BFD;
∵DF∥CA,
∴∠A=∠BFD,
∴∠FDE=∠A.
2.解:∵AB∥CD,∠B=50°,
∴∠BCD=∠B=50°,
∵CM平分∠BCD,
∴∠MCD=∠BCD=25°,
∵CM⊥CN,
∴∠MCN=90°,
∴∠ECN=180°﹣90°﹣25°=65°.
3.证明:过点P作PE∥AB,
∵直线AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠1+∠2=∠B+∠D,
即∠ABP+∠PDC=∠BPD.
4.解:∵CD是∠ACB的平分线,∠ACB=60°,
∴∠DCB=30°,
∵DE∥BC,
∴∠EDC=∠DCB=30°.
5.解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠FEA=∠A=40°,∠C=∠FEC,
∵∠AEC=70°,
∴∠FEC=∠AEC﹣∠FEA=70°﹣40°=30°.
∴∠C=30°.
故答案为:30°.
6.解:过点E、F分别作AB的平行线EG、FH,由平行线的传递性可得AB∥EG∥FH∥CD,
∵AB∥FH,
∴∠ABF=∠BFH,
∵FH∥CD,
∴∠CDF=∠DFH,
∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF;
同理可得∠BED=∠DEG+∠BEG=∠ABE+∠CDE;
∵3∠ABF=∠ABE,3∠CDF=∠CDE,
∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF=(∠ABE+∠CDE)=∠BED,
∴∠BED:∠BFD=3:1.
7.解:∵AB∥CD,
∴∠BEF+∠DFE=180°,
又∵EG平分∠BEF,FG平分∠DFE,
∴∠1=∠BEF,∠2=∠DFE,
∴∠1+∠2=(∠BEF+∠DFE)=×180°=90°,
∴∠EGF=180°﹣(∠1+∠2)=180°﹣90°=90°.
8.(1)解:∠EFG=∠FGD+∠BEF
证明:过点F作AB的平行线FH
∵AB∥CD,AB∥FH
∴CD∥FH(平行于同一条直线的两条直线互相平行)
∵AB∥FH(已作)
∴∠BEF=∠EFH(两直线平行,内错角相等)
∵CD∥FH(已证)
∴∠FGD=∠HFG(两直线平行,内错角相等
∴∠BEF+∠FGD=∠EFH+∠HFG(等量代换)
即:∠BEF+∠FGD=∠EFG
∴∠EFG=∠FGD+∠BEF
(2)EF⊥FG
证明:过点F作AB的平行线FH
∵AB∥CD,AB∥FH
∴CD∥FH(平行于同一条直线的两条直线互相平行)
∵∠AEF+∠BEF=180°(平角的定义)
∴∠BEF=180°﹣∠AEF=180°﹣150°=30°
∵AB∥FH(已作)
∴∠BEF=∠EFH(两直线平行,内错角相等)
∵CD∥FH(已证)
∴∠FGD=∠HFG(两直线平行,内错角相等)
∴∠BE+∠FGD=∠EFH+∠HFG(等量代换)
即:∠BEF+∠FGD=∠EFG
∴∠EFG=∠FGD+∠BEF=60°+30°=90°
∴EF⊥FG(垂直的定义)
9.解:∵AB∥CD∥EF,∠B=60°,∠EFC=45°,
∴∠ABC=∠BCD=60°,∠DCF=∠EFC=45°,
∴∠BCF=105°,
∵GC⊥CF,
∴∠GCF=90°,
∴∠BCG的度数为:105°﹣90°=15°.
10.解:如图,过点F作FH∥AB,
∵AB∥CD,
∴AB∥FH∥CD,
∴∠EFH=∠BEF=35°,∠CFH=∠C=20°,
∴∠CFE=∠EFH+∠CFH=35°+20°=55°,
∵FC平分∠EFG,
∴∠CFG=∠CFE=55°,
∴∠GFH=∠CFG+∠CFH=55°+20°=75°,
∵FH∥CD,
∴∠FGD=∠GFH=75°.
11.(1)证明:∵AB∥CD,
∴∠ABC=∠DCE,
∵AD∥BC,
∴∠ADC=∠DCE,
∴∠ABC=∠ADC,
(2)解:∵AB∥CD,
∴∠BAD=180°﹣∠ADC=180°﹣58°=122°,
∵AE平分∠BAD,
∴,
∵AD∥BC,
∴∠AEC=∠DAE=61°.
12.解:(1)∵AE分别平分∠CAM,
∴∠CAM=2∠EAM.
∵AM∥BN,
∴∠CAM=∠ACB,∠EAM=∠AEB.
∴∠ACB=2∠AEB.
(2)∵AM∥BN,
∴∠CAM=∠ACB,∠ADB=∠DAM.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵∠ADB﹣∠BAD=45°,
∴∠DAM﹣∠CAD=45°.
∴∠CAM=∠ACB=45°.
由(1)知∠ACB=2∠AEB,
∴∠AEB=22.5°.
13.解:(1)∵EF∥AD,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴DG∥BA,
∴∠B+∠BDG=180°,
∵∠B=55°,
∴∠BDG=125°;
(2)∠DGC+∠FEA=180°,
理由:∵AD平分∠BAC,
∴∠BAC=2∠3,
由(1)知,DG∥BA,
∴∠CGD=∠BAC,
∴∠CGD=2∠3,
∵EF∥AD,
∴∠FEA+∠3=180°,
∴∠DGC+∠FEA=180°.
14.证明:∵BF⊥AC,HE⊥AC,
∴BF∥EH.
∴∠H=∠ABF,∠2=∠FBC.
∵FG∥BC,
∴∠1=∠ABC.
∵∠ABC=∠ABF+∠FBC,
∴∠1=∠2+∠H.
15.解:(1)∠1=∠2.
理由:如图1,
∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2;
故答案为:∠1=∠2;
(2)∠1+∠2=180°,
理由:如图2,
∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°;
故答案为:∠1+∠2=180°;
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故答案为:一个角的两边与另一个角的两边分别平行,这两个角相等或互补;
(4)设另一个角为x°,根据以上结论得:
2x﹣30=x或2x﹣30+x=180°,
解得:x=30,或x=70,
这两个角度数为:30°、30°或110°,70°.
16.解:(1)证明:作EF∥AB,则EF∥AB∥CD,
∴∠1=∠B,∠2=∠D,
∴∠1+∠2=∠B+∠D,
即∠B+∠D=∠BED;
(2)∠BED+∠B+∠D=360°
证明:作EF∥AB,则EF∥AB∥CD,
∴∠1+∠B=180°,∠2+∠D=180°,
∴∠1+∠B+∠2+∠D=360°,
即∠BED+∠B+∠D=360°;
(3)∠BFE=∠FEC,
证明:作EG∥CD.
根据(1)可以得到∠BFE=∠B+∠FEG,
∵EG∥CD,
∴∠GEC=∠C,
又∵∠FEC=∠FEG+∠GEC,
∴∠FEC=∠BFE.
17.
解:(1)过K作KG∥AB,可得KG∥CD,
∴∠BEK=∠EKG,∠GKF=∠KFD,
∵EK、FK分别为∠BEF与∠EFD的平分线,
∴∠BEK=∠FEK,∠EFK=∠DFK,
∵AB∥CD,
∴∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠DFK)=180°,
∴∠BEK+∠DFK=90°,
则∠EKF=∠EKG+∠GKF=90°;
(2)∠K=2∠K1,理由为:
∵∠BEK、∠DFK的平分线相交于点K1,
∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,
∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,
∴∠BEK+∠KFD=90°,即∠KEK1+∠KFK1=45°,
∴∠K1=180°﹣(∠KEF+∠EFK)﹣(∠KEK1+∠KFK1)=45°,
则∠K=2∠K1;
(3)归纳总结得:∠Kn+1=×90°.
18.(1)证明:过点E作EK∥AB,如图1所示
∴∠ABE=∠BEK,
∵AB∥CD,
∴EK∥CD,
∴∠CEK+∠C=180°
∴∠ABE+∠C﹣∠BEC=∠BEC+∠CEK+∠C﹣∠BEC=∠CEK+∠C=180°;
(2)解:∵BF、EG分别平分∠ABE、∠BEC,
∴∠ABF=∠EBF,∠BEG=∠CEG,
设∠ABF=∠EBF=α,∠BEG=∠CEG=β,
∵BH∥EG,
∴∠HBE=∠BEG=β,
∴∠FBH=∠FBE﹣∠HBE=α﹣β,
由(1)知,∠ABE+∠C﹣∠BEC=180°,
即2α+∠C﹣2β=2(α﹣β)+∠C=180°,
∴2∠FBH+∠C=180°;
∵∠FBH=15°,
∴∠C=180°﹣2∠FBH=180°﹣2×15°=150°.
故答案为150°;
(3)解:∵CN、BF分别平分∠ECD、∠ABE,
∴∠ABF=∠EBF,∠ECN=∠DCN,
设∠ABF=∠EBF=x,∠ECN=∠DCN=y,
由(1)知:∠ABE+∠C﹣∠E=180°,
即∠E=2(x+y)﹣180°,
过M作PQ∥AB,
∵AB∥CD,
∴PQ∥CD,
则∠PMF=∠ABF=x,∠QMN=∠DCN=y,
∴∠FMN=180°﹣∠PMF﹣∠QMN=180°﹣(x+y),
∴∠E+∠FMN=x+y,
∵∠E+∠FMN=125°,
∴x+y=125°,
∴∠FMN=180°﹣(x+y)=180°﹣125°=55°.
19.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF.
(1)∵∠A=20°,∠C=40°,
∴∠1=∠A=20°,∠2=∠C=40°,
∴∠AEC=∠1+∠2=60°;
(2)∴∠1+∠A=180°,∠2+∠C=180°,
∵∠A=x°,∠C=y°,
∴∠1+∠2+x°+y°=360°,
∴∠AEC=360°﹣x°﹣y°;
(3)∠A=α,∠C=β,
∴∠1+∠A=180°,∠2=∠C=β,
∴∠1=180°﹣∠A=180°﹣α,
∴∠AEC=∠1+∠2=180°﹣α+β.
20.解:如图,过点F作FH//CD,
∵锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F,∠ECD=60°,∠ABE=100°,
∴∠DCM=∠ECM=30°,∠ABN=∠EBN=50°°,
∴∠NCF=30°,
∵AB∥CD,FH//CD,
∴FH∥AB,
∴∠HFB=∠ABN=50°,∠HFC=∠FCN=30°,
∴∠BFC=20°.
(2)如图,
∵BF∥CE,
∴∠ECM=∠BFM=α,
∴∠DCE=∠DNB=2α,
∵AB∥CD
∴∠ABN=∠BNC=2α,
∴∠ABE=4α.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
