苏科版七年级数学下册 12.2 证明 课件(共18张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 12.2 证明 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 09:51:04 | ||
图片预览



文档简介
(共18张PPT)
12.2 证明
知道吗?
180°
三角形3个内角的和是 .
°
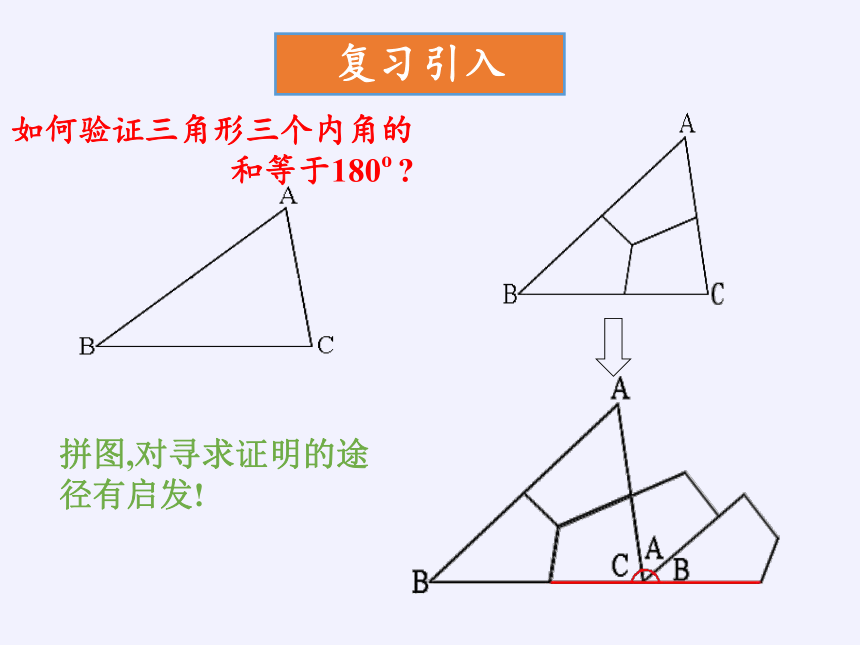
复习引入
如何验证三角形三个内角的和等于180o
拼图,对寻求证明的途径有启发!
复习引入
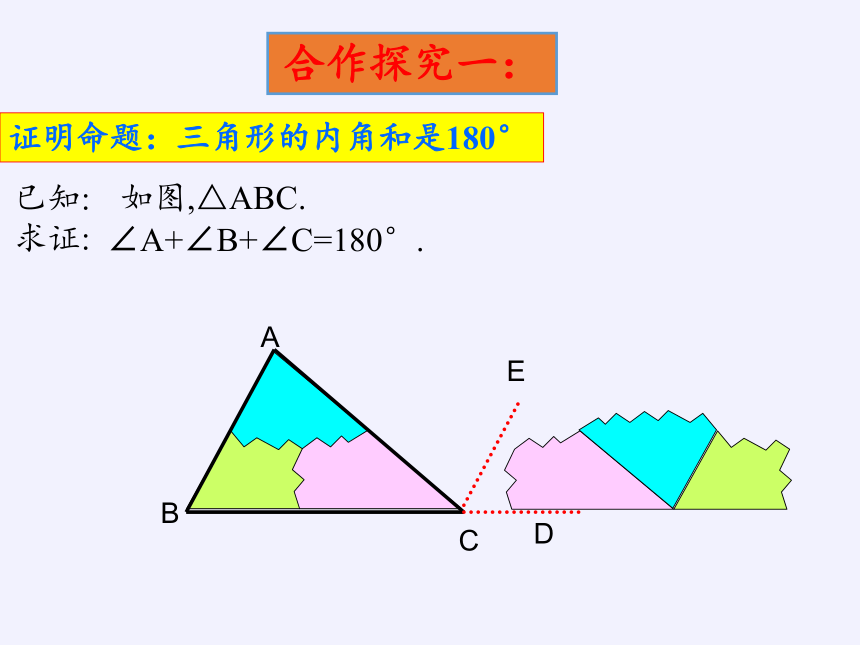
证明命题:三角形的内角和是180°
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
A
B
C
D
E
合作探究一:
A
B
C
2
1
D
E
已知:△ABC
求证:∠A+∠B+∠C=180°
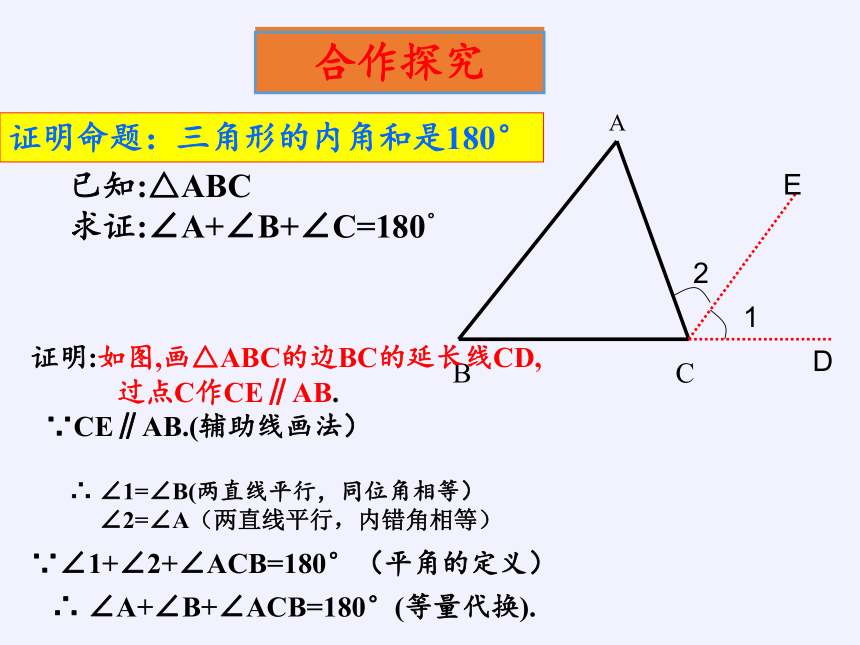
证明:如图,画△ABC的边BC的延长线CD,
过点C作CE∥AB.
∵CE∥AB.(辅助线画法)
∵∠1+∠2+∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠ACB=180°(等量代换).
探索发现
合作探究
证明命题:三角形的内角和是180°
∴ ∠1=∠B(两直线平行,同位角相等)
∠2=∠A(两直线平行,内错角相等)
关于辅助线
1.辅助线是为了证明需要在原图上添画的
线.(辅助线通常画成虚线)
2.它的作用是把分散的条件集中,把隐含
的条件显现出来,起到牵线搭桥的作用.
3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题
转化,但辅助线的添法没有一定的规律,
要根据需要而定,平时做题时要注意总结.
A
B
C
E
D
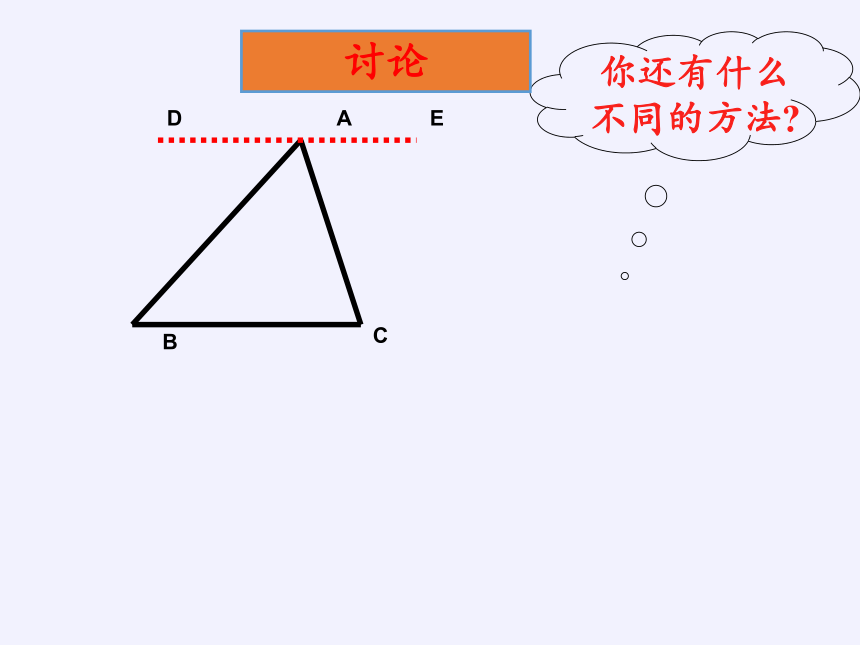
你还有什么
不同的方法
讨论
三角形内角和定理 :
三角形三个内角的和等于180°。
归纳总结
“因”
“果”
“依据”
A
B
C
D
已知:∠ACD是△ABC的一个外角.
求证:∠ACD=∠A+∠B.
在△ABC中,
∠A+∠B+∠ACB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠ACB(等式性质).
∵∠ACB+∠ACD=180°(平角的定义),
∴∠ACD =180°-∠ACB(等式性质).
∴∠ACD=∠ A+∠B (等量代换).
证明:
合作探究二:
思考:三角形的一个外角和与它不相邻的两个内角有怎样的数量关系?
由三角形的内角和定理,可以推出:
三角形的外角等于与它不相邻的两个内角的和.
归纳总结
像这样,由三角形内角和定理直接推出的正确结论,叫做这个三角形内角和定理的推论,它和定理一样,可以作为进一步证明的依据。
A
B
C
D
合作探究二:
几何语言表述:
∵∠ACD是△ABC的一个外角.
∴∠ACD=∠A+∠B.
例2 已知:如图,AC、BD相交于点O.
求证:∠A+∠B=∠C+∠D.
在△AOB中,
∠A+∠B+∠AOB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠AOB(等式性质).
在△COD中,同理得:∠C+∠D =180°-∠COD.
∵∠AOB=∠COD(对顶角相等).
∴∠A+∠B=∠C+∠D(等量代换).
证明:
B
A
C
D
O
交流展示
1.下列叙述中正确的是( )
A.三角形的外角等于两个内角的和
B. 三角形每一个内角都只有一个外角
C.三角形的外角等于与它不相邻的两个内角和
D.三角形的外角大于内角
检测练习
2. 如图,∠A+∠B+∠C+∠D+∠E+∠F等于( )
第2题图
检测练习
A.180° B.360° C.540° D.720°
已知:如图,AD是△ABC的角平分线,E是BC延长线上一点, ∠B = ∠EAC .
求证:∠ADE=∠DAE .
A
E
C
D
B
由条件你想到什么?
由结论你想到什么?
结合图形你想到什么?
1
2
拓展提升
本节课学习了哪些知识?掌握了什么技能?学到了哪些方法?获得了怎样的学习经验?
1.我们通过添加辅助线,把三角形的3个内角拼成1个平角;把三角形的3个内角拼成两平行线的同旁内角,证明了三角形内角和定理及推论.
2.继续感受数学的严谨、结论的确定,初步养成言之有理、落笔有据的推理习惯,发展初步的演绎推理能力.
课堂小结
知识树
三角形的内角和定理
推论
不同的证明方法
辅助线的作法、作用
转化角的方法
转化思想
谢 谢
12.2 证明
知道吗?
180°
三角形3个内角的和是 .
°
复习引入
如何验证三角形三个内角的和等于180o
拼图,对寻求证明的途径有启发!
复习引入
证明命题:三角形的内角和是180°
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
A
B
C
D
E
合作探究一:
A
B
C
2
1
D
E
已知:△ABC
求证:∠A+∠B+∠C=180°
证明:如图,画△ABC的边BC的延长线CD,
过点C作CE∥AB.
∵CE∥AB.(辅助线画法)
∵∠1+∠2+∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠ACB=180°(等量代换).
探索发现
合作探究
证明命题:三角形的内角和是180°
∴ ∠1=∠B(两直线平行,同位角相等)
∠2=∠A(两直线平行,内错角相等)
关于辅助线
1.辅助线是为了证明需要在原图上添画的
线.(辅助线通常画成虚线)
2.它的作用是把分散的条件集中,把隐含
的条件显现出来,起到牵线搭桥的作用.
3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题
转化,但辅助线的添法没有一定的规律,
要根据需要而定,平时做题时要注意总结.
A
B
C
E
D
你还有什么
不同的方法
讨论
三角形内角和定理 :
三角形三个内角的和等于180°。
归纳总结
“因”
“果”
“依据”
A
B
C
D
已知:∠ACD是△ABC的一个外角.
求证:∠ACD=∠A+∠B.
在△ABC中,
∠A+∠B+∠ACB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠ACB(等式性质).
∵∠ACB+∠ACD=180°(平角的定义),
∴∠ACD =180°-∠ACB(等式性质).
∴∠ACD=∠ A+∠B (等量代换).
证明:
合作探究二:
思考:三角形的一个外角和与它不相邻的两个内角有怎样的数量关系?
由三角形的内角和定理,可以推出:
三角形的外角等于与它不相邻的两个内角的和.
归纳总结
像这样,由三角形内角和定理直接推出的正确结论,叫做这个三角形内角和定理的推论,它和定理一样,可以作为进一步证明的依据。
A
B
C
D
合作探究二:
几何语言表述:
∵∠ACD是△ABC的一个外角.
∴∠ACD=∠A+∠B.
例2 已知:如图,AC、BD相交于点O.
求证:∠A+∠B=∠C+∠D.
在△AOB中,
∠A+∠B+∠AOB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠AOB(等式性质).
在△COD中,同理得:∠C+∠D =180°-∠COD.
∵∠AOB=∠COD(对顶角相等).
∴∠A+∠B=∠C+∠D(等量代换).
证明:
B
A
C
D
O
交流展示
1.下列叙述中正确的是( )
A.三角形的外角等于两个内角的和
B. 三角形每一个内角都只有一个外角
C.三角形的外角等于与它不相邻的两个内角和
D.三角形的外角大于内角
检测练习
2. 如图,∠A+∠B+∠C+∠D+∠E+∠F等于( )
第2题图
检测练习
A.180° B.360° C.540° D.720°
已知:如图,AD是△ABC的角平分线,E是BC延长线上一点, ∠B = ∠EAC .
求证:∠ADE=∠DAE .
A
E
C
D
B
由条件你想到什么?
由结论你想到什么?
结合图形你想到什么?
1
2
拓展提升
本节课学习了哪些知识?掌握了什么技能?学到了哪些方法?获得了怎样的学习经验?
1.我们通过添加辅助线,把三角形的3个内角拼成1个平角;把三角形的3个内角拼成两平行线的同旁内角,证明了三角形内角和定理及推论.
2.继续感受数学的严谨、结论的确定,初步养成言之有理、落笔有据的推理习惯,发展初步的演绎推理能力.
课堂小结
知识树
三角形的内角和定理
推论
不同的证明方法
辅助线的作法、作用
转化角的方法
转化思想
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
