人教版小学六年级小升初复习1.4数的运算(共40张PPT)
文档属性
| 名称 | 人教版小学六年级小升初复习1.4数的运算(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 14:08:38 | ||
图片预览











文档简介
(共40张PPT)
教学模板PPT
xxx版 二年级上
数的运算
回顾复习
+
-
×
÷
这节课我们就来系统地归纳、整理四则运算的知识。
课件PPT
1、我们学过哪些 运算?举例说明每种
运算的含义。
探索新知
1 )加法:把两个数合并成一个数的运算。
2 )减法: 已知两个数的和与其中一个加数,求另一个加数的运算。
算式:39+26=65
算式: 120-65=55
课件PPT
1、我们学过哪些 运算?举例说明每种运算的含义。
探索新知
3)乘法:求几个相同加数和的简便运算。
4)除法:已知两个数的积与其中一个因数,求另一个因数的运算。
算式:25×4=100
算式:40÷5=8
加法 和=( ) 一个加数=( )
减法
差=( ) 减数=( )
被减数=( )
乘法 积=( ) 一个因数=( )
除法 商=( ) 除数=( )
被除数=( )
加数+加数
和减另一个加数
被减数-减数
被减数-差
差+减数
因数×因数
积÷另一个因数
被除数÷除数
被除数÷商
商×除数
四则运算各部分之间的关系
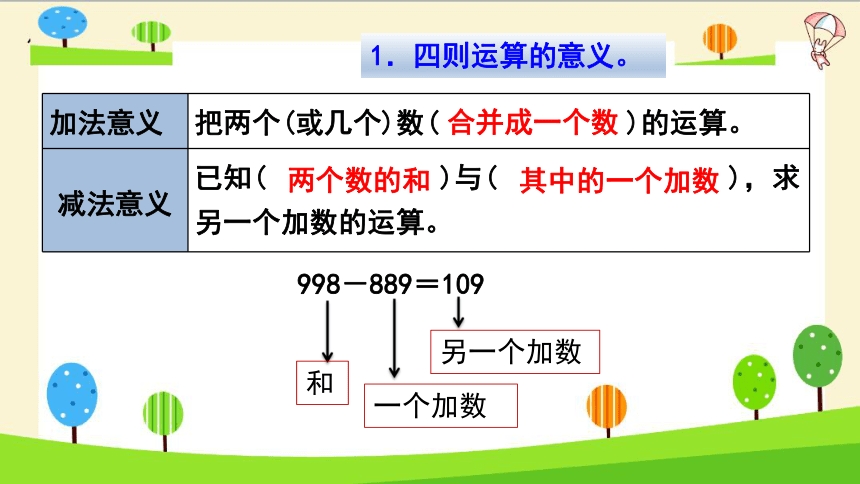
加法意义 把两个(或几个)数( )的运算。
减法意义 已知( )与( ),求另一个加数的运算。
合并成一个数
两个数的和
其中的一个加数
1.四则运算的意义。
998-889=109
和
一个加数
另一个加数
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
整数减法的计算方法:
相同数位对齐,从个位减起,哪一位上的数不够减,要从前一位退1,在本位上加十再减。
小数减法的计算方法:
把小数点对齐,从末位减起,如果被减数的小数末尾位数不够,可以添“0”再减。哪一位上的数不够减,要从前一位退1,在本位上加十再减。
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
分数加减法的计算方法:
同分母分数相加减,分母不变,只把分子相加减;
异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
注意:计算的结果要写成最简分数。
67.24
+108.89
3
1
1
1
1
6
7
1
.
70.43
-8.285
0
.
5
.
4
1
.
2
6
.
3083
+602
9103
30.83
+ 6.2
30.45
请分析错误的原因并改正
相同位数没有对齐,小数点没有对齐,没有通分。
例2.整数、小数、分数的运算法则有什么相同点?有什么不同点?
四则运算的法则
课件PPT
观察下列算式,说一说它们的运算方式
探索新知
26+32=58
58-26=32
58-32=26
1.6+2.7=4.3
4.3-1.6=2.7
4.3 -2.7=1.6
1.四则运算的意义。
乘法意义 ( )的简便运算。分数乘整数的意义与整数乘法的意义相同,一个数乘分数,就是求这个数的( )是多少。
除法意义 已知( )与( ),求另一个因数的运算。
求几个相同加数的和
几分之几
两个因数的积
其中的一个因数
1000÷8=125
积
一个因数
另一个因数
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
整数乘法的计算法则:
相同数位对齐,从末位算起,依次用第二个因数每位上的数去乘第一个因数,乘到哪一位,乘得的积的末位就和那一位对齐,然后把每次所乘得的积相加。(整数末尾有0的乘法:可以先把0前面的数相乘,然后看各因数的末尾一共有几个0,就在乘得的数的末尾添写几个0。)
整数除法的计算法则:
从被除数的最高位商起,除的时候,除数有几位,就先看被除数的前几位,如果前几位不够除,再多看一位。除到被除数的哪一位,就在那一位上面写上商; 每次除得的余数必须比除数小。
2.乘法和除法的法则
1 4 2
× 2 3
4 2 6
2 8 4
3 2 6 6
对照下面两道题,口述整数乘法和除法的计算法则
369
492
492
0
课件PPT
4、观察下列算式,说一说它们的运算方法
探索新知
125×8=100
1000÷125=8
1000÷8 =126
2.5×4=10
10÷2.5=4
10÷4=2.5
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
小数乘法的计算法则:
计算小数乘法,先按整数乘法的计算法则算出积,再看因数中一共有几位小数,就从积的末位起数出几位,点上小数点,得数的小数部分末尾有0,一般要把0去掉。
计算小数乘法,先按照整数乘法的法则算出积,再看乘数中一共有几位小数,就从积的右边起数出几位,点上小数点。
1.2×0.8 =
0.56×0.04 =
上
回
下
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
除数是整数的小数除法法则:
按照整数除法的法则去除,商的小数点要和被除数的小数点对齐,如果除到被除数的末尾仍有余数,就在余数后面补0,再继续除。
除数是小数的小数除法法则:
先看除数中有几位小数,就把被除数的小数点向右移动几位,数位不够的用0补足,然后按照除数是整数的小数除法来除。
224÷4=
56
除数是整数的小数除法:
2 2 . 4
.
22.4÷4=
4
5
2 0
6
2 4
0
……24个十分之一
5.6
2
4
商的小数点要和被除数的小数点对齐。
5 6
2 0
2 4
0
2 4
4
2 2 4
算一算,比一比
84÷4= 8.4÷4=
21
2.1
4
8 4
2 1
8
0
4
4
4
8. 4
2. 1
8
想一想,这两道题的计算方法哪些相同点和不同点呢?
相同点:整数除以整数与整数
除以小数计算方法相同。
不同点:小数除以整数要把商的小数点与被除数的小数点对齐。
0
4
4
0
2
2 4
6
·
0
5
6 0
0
2.5
被除数是整数,除数是一位小数
把被除数和除数同时X10,扩大到10倍
X10
X10
最后把商缩小10倍,或者说变回一位小数
.
2
1 1 0
0
2
被除数是一位小数,除数是两位小数
1.1
0.55
把被除数和除数同时X100,扩大到100倍
55
1 1 0
X100
X100
0.16 )9 .6 6.8 )34 0.25 )5
0
0
0 0
6
9 6
0
0
5
340
0
2
5 0
0
0
练一练:先说出下面各题怎样移动小数点,再计算。
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
小数乘法先按整数乘法计算法则计算,小数除法把除数转化成整数后,也按整数除法法则计算。
相同点:
小数乘、除法还要在计算结果上确定小数点的位置。
不同点:
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
分数的除法法则:
甲数除以乙数(0除外),等于甲数乘乙数的倒数。
分数乘法法则:
分数乘分数,用分数的分子相乘的积作为分子,分母相乘的积作为分母,为了计算简便,能约分的,可以先约分再乘。
相似点:分数除法要转化成分数乘法计算;
不同点:分数除法转化后乘的是除数的倒数。
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
加法
减法
整数
小数
分数
把两个数合并成一个数的运算。
与整数加法的意义相同。
与整数加法的意义相同。
已知两个数的和与其中的一个加数,求另一个加数的运算。
与整数减法的意义相同。
与整数减法的意义相同。
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
乘
法
除
法
整数
小数
分数
求几个相同加数的和的简便运算。
一个数与小数相乘,可以看作是求这个数的十分之几、百分之几…是多少。
一个数与分数相乘,可以看作是求这个数的几分之几是多少。
已知两个因数的积与其中的一个因数,求另一个因数的运算。
与整数除法的意义相同。
与整数除法的意义相同。
课件PPT
根据四则运算之间的关系,完成下列等式,并用字母表示这些关系。
加数+加数=和
另一个加数= 和-一个加数
被减数-减数=差
被减数-差=减数
差+减数=被减数
课件PPT
根据四则运算之间的关系,完成下列等式,并用用字母表示这些关系。
因数×因数=积
积÷一个因数=另一个因数
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
1、先算乘除,后算加减。如、96.45-23.65x4.2
2、同级运算从左往右算(加减同级,乘除同级)。9x4÷6 69-5+6
3、有括号的先算括号里面的,括号里面运算顺序同1、2。
(85+9÷3)-6.3+5.2
4、有括号先算小括号,再算中括号。
36-4x【63÷(9+6.35)÷ 6】
我们学过哪些 运算定律,请完成下表。
名称 定义 举例 用字母表示
加法 交换律 两个数相加,交换加粗线条的位置,它们的和不变。 15+28=28+15 a+b=b+a
加法 结合律 三个数相加,先把前两个数相加,再加上第三个数,或者先把后两个数相加,再和第一个数相加,它们的和不变。 (3+9)+1=3+(9+1) (a+b)+c=a+(b+c)
减法的 运算性质 从一个数里的依次减去两个数,等于这个数减去这两个数的和。 96-10-25=96-(10+25) a-b-c=a-(b+c)
一个数减去两个数的差,等于这个数先减去差里的被减数,然后再加上减数。 39-(35-6)=39-35+6 a-(b-c)=a-b+c
合理应用运算定律和性质计算下列各题,
并说一说应用了哪一种运算定律:
22+46+54
=22+(46+54)
=22+100
=122
3.25+0.257+6.75
=(3.25+6.75)+0.257
=10+0.257
=10.257
加法交换率和结合率
加法结合率
148-33-67
=148-(33+67)
=148-100
=48
589-23-66
=589-(23+66)
=148-89
=500
减法的运算性质
我们学过哪些 运算定律,请完成下表。
名称 定义 举例 用字母表示
乘法 交换律 两个数相乘,交换因数的位置,它们的积不变。 5×3=3×5 a×b=b×a
乘法 结合律 三个数相乘,先把前两个数相乘,再乘第三个数,或者先把后两个数相乘,再和第一个数相乘,它们的积不变。 (3×4)×5=3×(4×5) (a×b)×c=
a×(b×c)
乘法 分配律 两个的和与一个数相乘,可以的把两个加数分别与这个数相乘,再把两个积相加。 (2+4)×5=2×5+4×5 (a+b)×c=
a×c+b×c
除法的 运算性质 一个数依次除以两个数,等于这个数除以这两个数的积。 96÷2÷4=96÷(2x4) a÷b÷c=a÷(bxc)
25x19x4
=(25x4)x19
=100x19
=1900
合理应用运算定律和性质计算下列各题,
并说一说应用了哪一种运算定律:
36x72+64x72
=(36+64)x72
=100x72
=7200
乘法交换率和结合率
乘法交换率和分配率
32x15+6.8x150
=32x15+68x15
=(32x68)x15
=100x15
=1500
乘法交换率和分配率
https://www.21cnjy.com/help/help_extract.php
教学模板PPT
xxx版 二年级上
数的运算
回顾复习
+
-
×
÷
这节课我们就来系统地归纳、整理四则运算的知识。
课件PPT
1、我们学过哪些 运算?举例说明每种
运算的含义。
探索新知
1 )加法:把两个数合并成一个数的运算。
2 )减法: 已知两个数的和与其中一个加数,求另一个加数的运算。
算式:39+26=65
算式: 120-65=55
课件PPT
1、我们学过哪些 运算?举例说明每种运算的含义。
探索新知
3)乘法:求几个相同加数和的简便运算。
4)除法:已知两个数的积与其中一个因数,求另一个因数的运算。
算式:25×4=100
算式:40÷5=8
加法 和=( ) 一个加数=( )
减法
差=( ) 减数=( )
被减数=( )
乘法 积=( ) 一个因数=( )
除法 商=( ) 除数=( )
被除数=( )
加数+加数
和减另一个加数
被减数-减数
被减数-差
差+减数
因数×因数
积÷另一个因数
被除数÷除数
被除数÷商
商×除数
四则运算各部分之间的关系
加法意义 把两个(或几个)数( )的运算。
减法意义 已知( )与( ),求另一个加数的运算。
合并成一个数
两个数的和
其中的一个加数
1.四则运算的意义。
998-889=109
和
一个加数
另一个加数
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
整数减法的计算方法:
相同数位对齐,从个位减起,哪一位上的数不够减,要从前一位退1,在本位上加十再减。
小数减法的计算方法:
把小数点对齐,从末位减起,如果被减数的小数末尾位数不够,可以添“0”再减。哪一位上的数不够减,要从前一位退1,在本位上加十再减。
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
分数加减法的计算方法:
同分母分数相加减,分母不变,只把分子相加减;
异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
注意:计算的结果要写成最简分数。
67.24
+108.89
3
1
1
1
1
6
7
1
.
70.43
-8.285
0
.
5
.
4
1
.
2
6
.
3083
+602
9103
30.83
+ 6.2
30.45
请分析错误的原因并改正
相同位数没有对齐,小数点没有对齐,没有通分。
例2.整数、小数、分数的运算法则有什么相同点?有什么不同点?
四则运算的法则
课件PPT
观察下列算式,说一说它们的运算方式
探索新知
26+32=58
58-26=32
58-32=26
1.6+2.7=4.3
4.3-1.6=2.7
4.3 -2.7=1.6
1.四则运算的意义。
乘法意义 ( )的简便运算。分数乘整数的意义与整数乘法的意义相同,一个数乘分数,就是求这个数的( )是多少。
除法意义 已知( )与( ),求另一个因数的运算。
求几个相同加数的和
几分之几
两个因数的积
其中的一个因数
1000÷8=125
积
一个因数
另一个因数
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
整数乘法的计算法则:
相同数位对齐,从末位算起,依次用第二个因数每位上的数去乘第一个因数,乘到哪一位,乘得的积的末位就和那一位对齐,然后把每次所乘得的积相加。(整数末尾有0的乘法:可以先把0前面的数相乘,然后看各因数的末尾一共有几个0,就在乘得的数的末尾添写几个0。)
整数除法的计算法则:
从被除数的最高位商起,除的时候,除数有几位,就先看被除数的前几位,如果前几位不够除,再多看一位。除到被除数的哪一位,就在那一位上面写上商; 每次除得的余数必须比除数小。
2.乘法和除法的法则
1 4 2
× 2 3
4 2 6
2 8 4
3 2 6 6
对照下面两道题,口述整数乘法和除法的计算法则
369
492
492
0
课件PPT
4、观察下列算式,说一说它们的运算方法
探索新知
125×8=100
1000÷125=8
1000÷8 =126
2.5×4=10
10÷2.5=4
10÷4=2.5
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
小数乘法的计算法则:
计算小数乘法,先按整数乘法的计算法则算出积,再看因数中一共有几位小数,就从积的末位起数出几位,点上小数点,得数的小数部分末尾有0,一般要把0去掉。
计算小数乘法,先按照整数乘法的法则算出积,再看乘数中一共有几位小数,就从积的右边起数出几位,点上小数点。
1.2×0.8 =
0.56×0.04 =
上
回
下
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
除数是整数的小数除法法则:
按照整数除法的法则去除,商的小数点要和被除数的小数点对齐,如果除到被除数的末尾仍有余数,就在余数后面补0,再继续除。
除数是小数的小数除法法则:
先看除数中有几位小数,就把被除数的小数点向右移动几位,数位不够的用0补足,然后按照除数是整数的小数除法来除。
224÷4=
56
除数是整数的小数除法:
2 2 . 4
.
22.4÷4=
4
5
2 0
6
2 4
0
……24个十分之一
5.6
2
4
商的小数点要和被除数的小数点对齐。
5 6
2 0
2 4
0
2 4
4
2 2 4
算一算,比一比
84÷4= 8.4÷4=
21
2.1
4
8 4
2 1
8
0
4
4
4
8. 4
2. 1
8
想一想,这两道题的计算方法哪些相同点和不同点呢?
相同点:整数除以整数与整数
除以小数计算方法相同。
不同点:小数除以整数要把商的小数点与被除数的小数点对齐。
0
4
4
0
2
2 4
6
·
0
5
6 0
0
2.5
被除数是整数,除数是一位小数
把被除数和除数同时X10,扩大到10倍
X10
X10
最后把商缩小10倍,或者说变回一位小数
.
2
1 1 0
0
2
被除数是一位小数,除数是两位小数
1.1
0.55
把被除数和除数同时X100,扩大到100倍
55
1 1 0
X100
X100
0.16 )9 .6 6.8 )34 0.25 )5
0
0
0 0
6
9 6
0
0
5
340
0
2
5 0
0
0
练一练:先说出下面各题怎样移动小数点,再计算。
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
小数乘法先按整数乘法计算法则计算,小数除法把除数转化成整数后,也按整数除法法则计算。
相同点:
小数乘、除法还要在计算结果上确定小数点的位置。
不同点:
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
分数的除法法则:
甲数除以乙数(0除外),等于甲数乘乙数的倒数。
分数乘法法则:
分数乘分数,用分数的分子相乘的积作为分子,分母相乘的积作为分母,为了计算简便,能约分的,可以先约分再乘。
相似点:分数除法要转化成分数乘法计算;
不同点:分数除法转化后乘的是除数的倒数。
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
加法
减法
整数
小数
分数
把两个数合并成一个数的运算。
与整数加法的意义相同。
与整数加法的意义相同。
已知两个数的和与其中的一个加数,求另一个加数的运算。
与整数减法的意义相同。
与整数减法的意义相同。
课件PPT
2、整数、小数、分数的四则运算有什么相同点?
有什么不同点?
探索新知
乘
法
除
法
整数
小数
分数
求几个相同加数的和的简便运算。
一个数与小数相乘,可以看作是求这个数的十分之几、百分之几…是多少。
一个数与分数相乘,可以看作是求这个数的几分之几是多少。
已知两个因数的积与其中的一个因数,求另一个因数的运算。
与整数除法的意义相同。
与整数除法的意义相同。
课件PPT
根据四则运算之间的关系,完成下列等式,并用字母表示这些关系。
加数+加数=和
另一个加数= 和-一个加数
被减数-减数=差
被减数-差=减数
差+减数=被减数
课件PPT
根据四则运算之间的关系,完成下列等式,并用用字母表示这些关系。
因数×因数=积
积÷一个因数=另一个因数
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
1、先算乘除,后算加减。如、96.45-23.65x4.2
2、同级运算从左往右算(加减同级,乘除同级)。9x4÷6 69-5+6
3、有括号的先算括号里面的,括号里面运算顺序同1、2。
(85+9÷3)-6.3+5.2
4、有括号先算小括号,再算中括号。
36-4x【63÷(9+6.35)÷ 6】
我们学过哪些 运算定律,请完成下表。
名称 定义 举例 用字母表示
加法 交换律 两个数相加,交换加粗线条的位置,它们的和不变。 15+28=28+15 a+b=b+a
加法 结合律 三个数相加,先把前两个数相加,再加上第三个数,或者先把后两个数相加,再和第一个数相加,它们的和不变。 (3+9)+1=3+(9+1) (a+b)+c=a+(b+c)
减法的 运算性质 从一个数里的依次减去两个数,等于这个数减去这两个数的和。 96-10-25=96-(10+25) a-b-c=a-(b+c)
一个数减去两个数的差,等于这个数先减去差里的被减数,然后再加上减数。 39-(35-6)=39-35+6 a-(b-c)=a-b+c
合理应用运算定律和性质计算下列各题,
并说一说应用了哪一种运算定律:
22+46+54
=22+(46+54)
=22+100
=122
3.25+0.257+6.75
=(3.25+6.75)+0.257
=10+0.257
=10.257
加法交换率和结合率
加法结合率
148-33-67
=148-(33+67)
=148-100
=48
589-23-66
=589-(23+66)
=148-89
=500
减法的运算性质
我们学过哪些 运算定律,请完成下表。
名称 定义 举例 用字母表示
乘法 交换律 两个数相乘,交换因数的位置,它们的积不变。 5×3=3×5 a×b=b×a
乘法 结合律 三个数相乘,先把前两个数相乘,再乘第三个数,或者先把后两个数相乘,再和第一个数相乘,它们的积不变。 (3×4)×5=3×(4×5) (a×b)×c=
a×(b×c)
乘法 分配律 两个的和与一个数相乘,可以的把两个加数分别与这个数相乘,再把两个积相加。 (2+4)×5=2×5+4×5 (a+b)×c=
a×c+b×c
除法的 运算性质 一个数依次除以两个数,等于这个数除以这两个数的积。 96÷2÷4=96÷(2x4) a÷b÷c=a÷(bxc)
25x19x4
=(25x4)x19
=100x19
=1900
合理应用运算定律和性质计算下列各题,
并说一说应用了哪一种运算定律:
36x72+64x72
=(36+64)x72
=100x72
=7200
乘法交换率和结合率
乘法交换率和分配率
32x15+6.8x150
=32x15+68x15
=(32x68)x15
=100x15
=1500
乘法交换率和分配率
https://www.21cnjy.com/help/help_extract.php
