2022年最新强化训练沪教版(上海)九年级数学第二学期 第二十七章圆与正多边形 章节练习试卷(word版 含解析)
文档属性
| 名称 | 2022年最新强化训练沪教版(上海)九年级数学第二学期 第二十七章圆与正多边形 章节练习试卷(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 613.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 14:32:28 | ||
图片预览



文档简介
九年级数学第二学期第二十七章圆与正多边形章节练习
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,中的半径为1,内接于.若,,则的长是( )
A. B. C. D.
2、已知⊙O的半径为3,点P到圆心O的距离为4,则点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O上 C.点P在⊙O内 D.无法确定
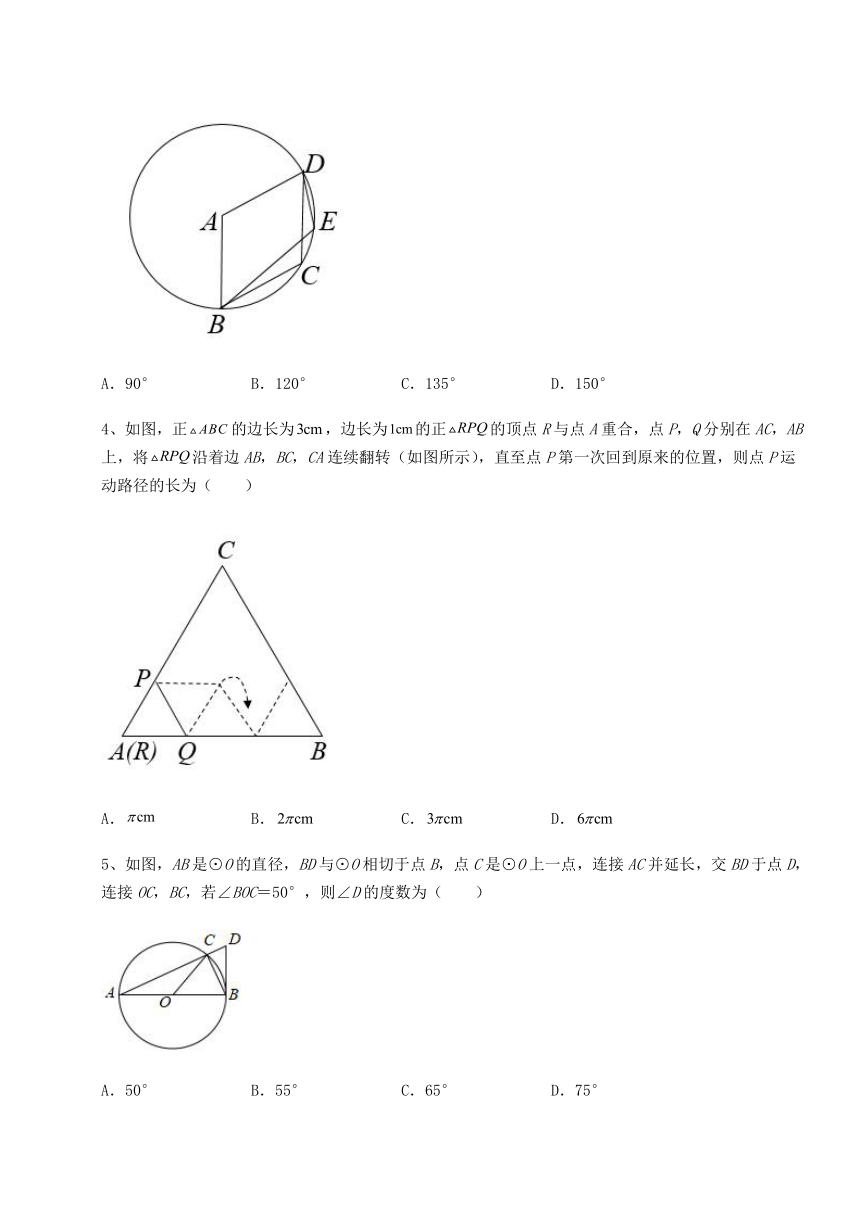
3、如图,菱形ABCD的顶点B,C,D均在⊙A上,点E在弧BD上,则∠BED的度数为( )
A.90° B.120° C.135° D.150°
4、如图,正的边长为,边长为的正的顶点R与点A重合,点P,Q分别在AC,AB上,将沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为( )
A. B. C. D.
5、如图,AB是⊙O的直径,BD与⊙O相切于点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )
A.50° B.55° C.65° D.75°
6、如图,中,,,点是边上一动点,连接,以为直径的圆交于点.若长为4,则线段长的最小值为( )
A. B. C. D.
7、若正六边形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3 B.6,3 C.3,6 D.6,3
8、如图,作,,;以A为圆心,以AC长为半径画弧,交斜边AB与点D;以B为圆心,以BD长为半径画弧,交BC与点E.若,则( )
A. B. C. D.
9、如图,BD是⊙O的切线,∠BCE=30°,则∠D=( )
A.40° B.50° C.60° D.30°
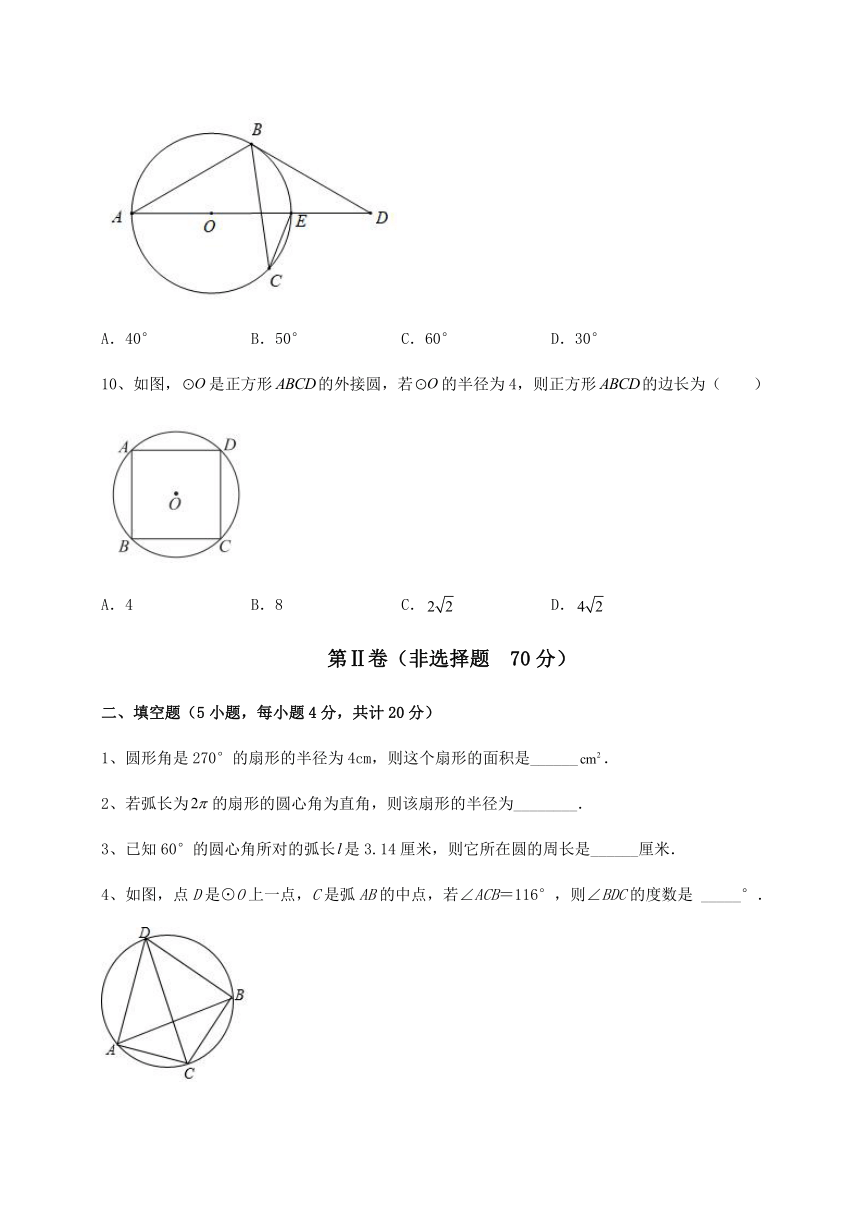
10、如图,是正方形的外接圆,若的半径为4,则正方形的边长为( )
A.4 B.8 C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、圆形角是270°的扇形的半径为4cm,则这个扇形的面积是______.
2、若弧长为的扇形的圆心角为直角,则该扇形的半径为________.
3、已知60°的圆心角所对的弧长是3.14厘米,则它所在圆的周长是______厘米.
4、如图,点D是⊙O上一点,C是弧AB的中点,若∠ACB=116°,则∠BDC的度数是 _____°.
5、如图,点A、B、C、D、E在上,且弧AB为,则________.
三、解答题(5小题,每小题10分,共计50分)
1、已知:如图,射线.
求作:,使得点在射线上,,.
作法:①在射线上任取一点;
②以点为圆心,的长为半径画圆,交射线于另一点;
③以点为圆心,的长为半径画弧,在射线上方交于点;
④连接、.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:为的直径,点在上,
(___________________________)(填推理依据).
连接.
,
为等边三角形(___________________________)(填推理依据).
所以为所求作的三角形.
2、已知:如图,A为上的一点.
求作:过点A且与相切的一条直线.
作法:①连接OA;
②以点A为圆心,OA长为半径画弧,与的一个交点为B,作射线OB;
③以点B为圆心,OA长为半径画弧,交射线OB于点P(不与点O重合);
④作直线PA.
直线PA即为所求.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接BA.
由作法可知.
∴点A在以OP为直径的圆上.
∴( )(填推理的依据).
∵OA是的半径,
∴直线PA与相切( )(填推理的依据).
3、如图,在正方形网格中,每一个小正方形的边长都为1,△ABC的顶点分别为A(2,3),B(2,1),C(5,4).
(1)只用直尺在图中找出△ABC的外心P,并写出P点的坐标_____________
(2)以(1)中的外心P为位似中心,按位似比2:1在位似中心的左侧将△ABC放大为△A′B′C′,放大后点A、B、C的对应点分别为A′、B′、C′,请在图中画出△A′B′C′;
(3)若以A为圆心,为半径的⊙A与线段BC有公共点, 则的取值范围是____________.
4、如图,⊙O是四边形ABCD的外接圆,AD为⊙O的直径.连结BD,若.
(1)求证:∠1=∠2.
(2)当AD=4,BC=4时,求ABD的面积.
5、如图,在△ABC中,∠A=∠B=30°.
(1)尺规作图:在线段AB上找一点O,以O为圆心作圆,使⊙O经过B,C两点.
(2)求证:AC与(1)中所做的⊙O相切.
-参考答案-
一、单选题
1、B
【分析】
连接OA、OB,过点O作,由三角形内角和求出,由圆周角定理可得,由得是等腰三角形,即可知,,根据三角函数已可求出AD,进而得出答案.
【详解】
如图,连接OA、OB,过点O作,
∵,,
∴,
∴,
∵,
∴是等腰三角形,
∴,,
∴,
∴,,
∴.
故选:B.
【点睛】
本题主要考查了圆周角定理,解题的关键在于能够熟练掌握圆周角定理.
2、A
【分析】
根据点与圆心的距离与半径的大小关系即可确定点P与⊙O的位置关系.
【详解】
解:∵⊙O的半径分别是3,点P到圆心O的距离为4,
∴d>r,
∴点P与⊙O的位置关系是:点在圆外.
故选:A.
【点睛】
本题主要考查了点与圆的位置关系,准确分析判断是解题的关键.
3、B
【分析】
连接AC,根据菱形的性质得到△ABC、△ACD是等边三角形,求出∠BCD=120°,再根据圆周角定理即可求解.
【详解】
如图,连接AC
∴AC=AB=AD
∵四边形ABCD是菱形
∴AB=BC=AD=CD=AC
∴△ABC、△ACD是等边三角形
∴∠ACB=∠ACD=60°
∴∠BCD=120°
∵优弧
∴∠BED=∠BCD=120°
故选B.
【点睛】
此题主要考查圆内角度求解,解题的关键是熟知菱形的性质及圆周角定理.
4、B
【分析】
从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,第二次是以点P为圆心,所以没有路程,同理在AC和BC上也是相同的情况,由此求解即可.
【详解】
解:从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,所以弧长=,第二次是以点P为圆心,所以没有路程,在BC边上,第一次,第二次同样没有路程,AC边上也是如此,点P运动路径的长为×3=2π.
故选:B.
【点睛】
本题主要考查了等边三角形的性质,求弧长,解题的关键在于能够根据题意得到P点的运动轨迹.
5、C
【分析】
首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】
解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
【点睛】
本题考查的是切线的性质、圆周角定理,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.
6、D
【分析】
如图,连接 由为直径,证明在以的中点为圆心,为直径的上运动,连接 交于点 则此时最小,再利用锐角的正弦与勾股定理分别求解,即可得到答案.
【详解】
解:如图,连接 由为直径,
在以的中点为圆心,为直径的上运动,
连接 交于点 则此时最小,
,,
故选D
【点睛】
本题考查的是勾股定理的应用,圆外一点与圆的最短距离的理解,锐角的正弦的应用,掌握“圆外一点与圆的最短距离求解线段的最小值”是解本题的关键.
7、B
【分析】
如图1,⊙O是正六边形的外接圆,连接OA,OB,求出∠AOB=60°,即可证明△OAB是等边三角形,得到OA=AB=6;如图2,⊙O1是正六边形的内切圆,连接O1A,O1B,过点O1作O1M⊥AB于M,先求出∠AO1B=60°,然后根据等边三角形的性质和勾股定理求解即可.
【详解】
解:(1)如图1,⊙O是正六边形的外接圆,连接OA,OB,
∵六边形ABCDEF是正六边形,
∴∠AOB=360°÷6=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴OA=AB=6;
(2)如图2,⊙O1是正六边形的内切圆,连接O1A,O1B,过点O1作O1M⊥AB于M,
∵六边形ABCDEF是正六边形,
∴∠AO1B=60°,
∵O1A= O1B,
∴△O1AB是等边三角形,
∴O1A= AB=6,
∵O1M⊥AB,
∴∠O1MA=90°,AM=BM,
∵AB=6,
∴AM=BM,
∴O1M.
故选B.
【点睛】
本题主要考查了正多边形与圆,等边三角形的性质与判定,勾股定理,熟知正多边形与圆的知识是解题的关键.
8、A
【分析】
根据勾股定理求出AB,再根据圆的定义可求得AD=AC,BE=BD即可求解.
【详解】
解:∵,,
∴AC=3,
在中,,由勾股定理得:
,
由题意,AD=AC=3,BE=BD=AB-AD=-3,
∴CE=BC-BE=6-(-3)=9-,
故选:A.
【点睛】
本题考查圆的定义、勾股定理,熟练掌握勾股定理是解答的关键.
9、D
【分析】
连接,根据同弧所对的圆周角相等,等角对等边,三角形的外角性质可得,根据切线的性质可得,根据直角三角形的两个锐角互余即可求得.
【详解】
解:连接
BD是⊙O的切线
故选D
【点睛】
本题考查了切线的性质,等弧所对的圆周角相等,直角三角形的两锐角互余,掌握切线的性质是解题的关键.
10、D
【分析】
连接OB,OC,过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
【详解】
解:连接OB,OC,过点O作OE⊥BC于点E,
∴OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴,
∴BC=2BE=,即正方形ABCD的边长是.
故选:D
【点睛】
本题考查的是圆周角定理、垂径定理及勾股定理,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.
二、填空题
1、12π
【分析】
根据扇形的面积公式计算即可.
【详解】
∵
=12π,
故答案为:12π.
【点睛】
本题考查了扇形的面积,熟记扇形面积公式是解题的关键.
2、4
【分析】
利用扇形的弧长公式表示出扇形的弧长,将已知的圆心角及弧长代入,即可求出扇形的半径.
【详解】
解:∵扇形的圆心角为90°,弧长为2π,
∴,
即,
则扇形的半径r=4.
故答案为:4.
【点睛】
本题考查了弧长的计算公式,扇形的弧长公式为(n为扇形的圆心角度数,r为扇形的半径),熟练掌握弧长公式是解本题的关键.
3、18.84
【分析】
先根据弧长公式求得πr,然后再运用圆的周长公式解答即可.
【详解】
解:设圆弧所在圆的半径为厘米,
则,
解得,
则它所在圆的周长为(厘米),
故答案为:.
【点睛】
本题主要考查了弧长公式、圆的周长公式等知识点,牢记弧长公式是解答本题的关键.
4、32
【分析】
根据圆内接四边形的性质得出∠ADB+∠ACB=180°,求出∠ADB=64°,根据C是弧AB的中点求出,根据圆周角定理得出∠BDC=∠ADC=ADB,再求出答案即可.
【详解】
解:∵A、C、B、D四点共圆,
∴∠ADB+∠ACB=180°,
∵∠ACB=116°,
∴∠ADB=180°﹣116°=64°,
∵C是弧AB的中点,
∴,
∴∠BDC=∠ADC=ADB=32°,
故答案为:32.
【点睛】
本题考查四点共圆性质,圆周角与弧的关系,掌握四点共圆性质,圆周角与弧的关系是解题关键.
5、
【分析】
先根据弧的度数与它所对应的圆心角的度数的关系,求得弧对应的圆心角的度数,再根据圆周角与圆心角的关系,则可求得.
【详解】
弧的度数等于它所对应的圆心角的度数,由于弧为,所以 ,
顶点在圆上且两边都和圆相交的角叫做圆周角,而一条弧所对的圆周角等于它所对的圆心角的一半,所以:
, ,
,
故答案为:.
【点睛】
本题考查弧、圆周角、圆心角的概念,及它们之间的关系,熟知同弧所对的圆周角等于圆心角的一半是解本题的关键.
三、解答题
1、
(1)图形见解析
(2)直径所对的圆周角是直角;三边相等的三角形是等边三角形.
【分析】
(1)根据要求作出图形即可;
(2)根据圆周角定理等边三角形的判定和性质解决问题即可.
(1)
如图,△ABC即为所求作.
(2)
∵AB为⊙O的直径,点C在⊙O上,
∴∠ACB=90°(直径所对的圆周角是直角),
连接OC.
∵OA=OC=AC,
∴△AOC为等边三角形(三边相等的三角形是等边三角形),
∴∠A=60°.
故答案为:直径所对的圆周角是直角,三边相等的三角形是等边三角形.
【点睛】
本题考查作图-复杂作图,等边三角形的判定和性质,圆周角定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
2、(1)图见解析;(2)直径所对的圆周角是直角,切线的判定定理
【分析】
(1)根据所给的几何语言作出对应的图形即可;
(2)根据圆周角定理和切线的判定定理解答即可.
【详解】
解:(1)补全图形如图所示,直线AP即为所求作;
(2)证明:连接BA,
由作法可知,
∴点A在以OP为直径的圆上,
∴(直径所对的圆周角是直角),
∵OA是的半径,
∴直线PA与相切(切线的判定定理),
故答案为:直径所对的圆周角是直角,切线的判定定理.
【点睛】
本题考查基本作图-画圆、圆周角定理、切线的判定定理,熟知复杂作图是在基本作图的基础上进行作图,一般是结合几何图形的性质,因此熟练掌握基本图形的性质和切线的判定是解答的关键.
3、(1)(4,2);(2)见解析;(3)
【分析】
(1)根据三角形的外接圆的圆心是三边垂直平分线的交点即可找到点P;
(2)根据位似中心与三角形三个顶点的连线将原三角形扩大2倍即可;
(3)根据直线和圆的位置关系:当半径大于或等于点A到BC的距离时,⊙A与线段BC有一个或两个公共点即可.
【详解】
解:如图所示:
(1)点P即为△ABC的外心,P点的坐标为(4,2),
故答案为:(4,2);
(2)图中画出的△A′B′C′即为所求作的图形;
(3)观察图形可知:r=时,⊙A与线段BC有一个公共点.
此时⊙A与线段BC相切,
当时,⊙A只经过点,
∴的取值范围是
故答案为:.
【点睛】
本题考查了作图 位似变换、三角形的外接圆与圆心、直线与圆的位置关系,解决本题的关键是根据位似中心画位似图形.
4、(1)见解析;(2)
【分析】
(1)先证明,再根据同圆中,等弧所对的圆周角相等即可证明;
(2)过O点作OE⊥BC于点E,连接OB,由垂径定理可得BE=CE=,由勾股定理求出,即可得到.
【详解】
解:(1)∵,
∴,
∴,
∴∠1=∠2;
(2)过O点作OE⊥BC于点E,连接OB,
∴BE=CE=,
∵AD为⊙O的直径,
∴OB=,
∴,
∴.
【点睛】
本题主要考查了垂径定理,勾股定理,同圆中等弧所对的圆周角相等,解题的关键在于能够熟练掌握圆的相关知识.
5、(1)答案见解析 (2)答案见解析
【分析】
(1)作线段BC的垂直平分线MN,交AB于点O,以O为圆心,OB为半径作⊙O 即可;
(2)连接OC,证明∠ACB= 120°,再证明∠ACO= 90°,即可得答案.
【详解】
解:(1)如下图,⊙O即为所作:
(2)证明:连接OC
∵△ABC中,∠A=∠B= 30°
∴∠ACB= 120°
由(1) 可知,OC= OB
∴∠OCB=∠B = 30°
∴∠ACO= 90°
∴AC是⊙O的相切.
【点睛】
本题考查作图-垂直平分线、圆的画法,等腰三角形的性质,切线的判定等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,中的半径为1,内接于.若,,则的长是( )
A. B. C. D.
2、已知⊙O的半径为3,点P到圆心O的距离为4,则点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O上 C.点P在⊙O内 D.无法确定
3、如图,菱形ABCD的顶点B,C,D均在⊙A上,点E在弧BD上,则∠BED的度数为( )
A.90° B.120° C.135° D.150°
4、如图,正的边长为,边长为的正的顶点R与点A重合,点P,Q分别在AC,AB上,将沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为( )
A. B. C. D.
5、如图,AB是⊙O的直径,BD与⊙O相切于点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )
A.50° B.55° C.65° D.75°
6、如图,中,,,点是边上一动点,连接,以为直径的圆交于点.若长为4,则线段长的最小值为( )
A. B. C. D.
7、若正六边形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3 B.6,3 C.3,6 D.6,3
8、如图,作,,;以A为圆心,以AC长为半径画弧,交斜边AB与点D;以B为圆心,以BD长为半径画弧,交BC与点E.若,则( )
A. B. C. D.
9、如图,BD是⊙O的切线,∠BCE=30°,则∠D=( )
A.40° B.50° C.60° D.30°
10、如图,是正方形的外接圆,若的半径为4,则正方形的边长为( )
A.4 B.8 C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、圆形角是270°的扇形的半径为4cm,则这个扇形的面积是______.
2、若弧长为的扇形的圆心角为直角,则该扇形的半径为________.
3、已知60°的圆心角所对的弧长是3.14厘米,则它所在圆的周长是______厘米.
4、如图,点D是⊙O上一点,C是弧AB的中点,若∠ACB=116°,则∠BDC的度数是 _____°.
5、如图,点A、B、C、D、E在上,且弧AB为,则________.
三、解答题(5小题,每小题10分,共计50分)
1、已知:如图,射线.
求作:,使得点在射线上,,.
作法:①在射线上任取一点;
②以点为圆心,的长为半径画圆,交射线于另一点;
③以点为圆心,的长为半径画弧,在射线上方交于点;
④连接、.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:为的直径,点在上,
(___________________________)(填推理依据).
连接.
,
为等边三角形(___________________________)(填推理依据).
所以为所求作的三角形.
2、已知:如图,A为上的一点.
求作:过点A且与相切的一条直线.
作法:①连接OA;
②以点A为圆心,OA长为半径画弧,与的一个交点为B,作射线OB;
③以点B为圆心,OA长为半径画弧,交射线OB于点P(不与点O重合);
④作直线PA.
直线PA即为所求.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接BA.
由作法可知.
∴点A在以OP为直径的圆上.
∴( )(填推理的依据).
∵OA是的半径,
∴直线PA与相切( )(填推理的依据).
3、如图,在正方形网格中,每一个小正方形的边长都为1,△ABC的顶点分别为A(2,3),B(2,1),C(5,4).
(1)只用直尺在图中找出△ABC的外心P,并写出P点的坐标_____________
(2)以(1)中的外心P为位似中心,按位似比2:1在位似中心的左侧将△ABC放大为△A′B′C′,放大后点A、B、C的对应点分别为A′、B′、C′,请在图中画出△A′B′C′;
(3)若以A为圆心,为半径的⊙A与线段BC有公共点, 则的取值范围是____________.
4、如图,⊙O是四边形ABCD的外接圆,AD为⊙O的直径.连结BD,若.
(1)求证:∠1=∠2.
(2)当AD=4,BC=4时,求ABD的面积.
5、如图,在△ABC中,∠A=∠B=30°.
(1)尺规作图:在线段AB上找一点O,以O为圆心作圆,使⊙O经过B,C两点.
(2)求证:AC与(1)中所做的⊙O相切.
-参考答案-
一、单选题
1、B
【分析】
连接OA、OB,过点O作,由三角形内角和求出,由圆周角定理可得,由得是等腰三角形,即可知,,根据三角函数已可求出AD,进而得出答案.
【详解】
如图,连接OA、OB,过点O作,
∵,,
∴,
∴,
∵,
∴是等腰三角形,
∴,,
∴,
∴,,
∴.
故选:B.
【点睛】
本题主要考查了圆周角定理,解题的关键在于能够熟练掌握圆周角定理.
2、A
【分析】
根据点与圆心的距离与半径的大小关系即可确定点P与⊙O的位置关系.
【详解】
解:∵⊙O的半径分别是3,点P到圆心O的距离为4,
∴d>r,
∴点P与⊙O的位置关系是:点在圆外.
故选:A.
【点睛】
本题主要考查了点与圆的位置关系,准确分析判断是解题的关键.
3、B
【分析】
连接AC,根据菱形的性质得到△ABC、△ACD是等边三角形,求出∠BCD=120°,再根据圆周角定理即可求解.
【详解】
如图,连接AC
∴AC=AB=AD
∵四边形ABCD是菱形
∴AB=BC=AD=CD=AC
∴△ABC、△ACD是等边三角形
∴∠ACB=∠ACD=60°
∴∠BCD=120°
∵优弧
∴∠BED=∠BCD=120°
故选B.
【点睛】
此题主要考查圆内角度求解,解题的关键是熟知菱形的性质及圆周角定理.
4、B
【分析】
从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,第二次是以点P为圆心,所以没有路程,同理在AC和BC上也是相同的情况,由此求解即可.
【详解】
解:从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,所以弧长=,第二次是以点P为圆心,所以没有路程,在BC边上,第一次,第二次同样没有路程,AC边上也是如此,点P运动路径的长为×3=2π.
故选:B.
【点睛】
本题主要考查了等边三角形的性质,求弧长,解题的关键在于能够根据题意得到P点的运动轨迹.
5、C
【分析】
首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】
解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
【点睛】
本题考查的是切线的性质、圆周角定理,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.
6、D
【分析】
如图,连接 由为直径,证明在以的中点为圆心,为直径的上运动,连接 交于点 则此时最小,再利用锐角的正弦与勾股定理分别求解,即可得到答案.
【详解】
解:如图,连接 由为直径,
在以的中点为圆心,为直径的上运动,
连接 交于点 则此时最小,
,,
故选D
【点睛】
本题考查的是勾股定理的应用,圆外一点与圆的最短距离的理解,锐角的正弦的应用,掌握“圆外一点与圆的最短距离求解线段的最小值”是解本题的关键.
7、B
【分析】
如图1,⊙O是正六边形的外接圆,连接OA,OB,求出∠AOB=60°,即可证明△OAB是等边三角形,得到OA=AB=6;如图2,⊙O1是正六边形的内切圆,连接O1A,O1B,过点O1作O1M⊥AB于M,先求出∠AO1B=60°,然后根据等边三角形的性质和勾股定理求解即可.
【详解】
解:(1)如图1,⊙O是正六边形的外接圆,连接OA,OB,
∵六边形ABCDEF是正六边形,
∴∠AOB=360°÷6=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴OA=AB=6;
(2)如图2,⊙O1是正六边形的内切圆,连接O1A,O1B,过点O1作O1M⊥AB于M,
∵六边形ABCDEF是正六边形,
∴∠AO1B=60°,
∵O1A= O1B,
∴△O1AB是等边三角形,
∴O1A= AB=6,
∵O1M⊥AB,
∴∠O1MA=90°,AM=BM,
∵AB=6,
∴AM=BM,
∴O1M.
故选B.
【点睛】
本题主要考查了正多边形与圆,等边三角形的性质与判定,勾股定理,熟知正多边形与圆的知识是解题的关键.
8、A
【分析】
根据勾股定理求出AB,再根据圆的定义可求得AD=AC,BE=BD即可求解.
【详解】
解:∵,,
∴AC=3,
在中,,由勾股定理得:
,
由题意,AD=AC=3,BE=BD=AB-AD=-3,
∴CE=BC-BE=6-(-3)=9-,
故选:A.
【点睛】
本题考查圆的定义、勾股定理,熟练掌握勾股定理是解答的关键.
9、D
【分析】
连接,根据同弧所对的圆周角相等,等角对等边,三角形的外角性质可得,根据切线的性质可得,根据直角三角形的两个锐角互余即可求得.
【详解】
解:连接
BD是⊙O的切线
故选D
【点睛】
本题考查了切线的性质,等弧所对的圆周角相等,直角三角形的两锐角互余,掌握切线的性质是解题的关键.
10、D
【分析】
连接OB,OC,过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
【详解】
解:连接OB,OC,过点O作OE⊥BC于点E,
∴OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴,
∴BC=2BE=,即正方形ABCD的边长是.
故选:D
【点睛】
本题考查的是圆周角定理、垂径定理及勾股定理,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.
二、填空题
1、12π
【分析】
根据扇形的面积公式计算即可.
【详解】
∵
=12π,
故答案为:12π.
【点睛】
本题考查了扇形的面积,熟记扇形面积公式是解题的关键.
2、4
【分析】
利用扇形的弧长公式表示出扇形的弧长,将已知的圆心角及弧长代入,即可求出扇形的半径.
【详解】
解:∵扇形的圆心角为90°,弧长为2π,
∴,
即,
则扇形的半径r=4.
故答案为:4.
【点睛】
本题考查了弧长的计算公式,扇形的弧长公式为(n为扇形的圆心角度数,r为扇形的半径),熟练掌握弧长公式是解本题的关键.
3、18.84
【分析】
先根据弧长公式求得πr,然后再运用圆的周长公式解答即可.
【详解】
解:设圆弧所在圆的半径为厘米,
则,
解得,
则它所在圆的周长为(厘米),
故答案为:.
【点睛】
本题主要考查了弧长公式、圆的周长公式等知识点,牢记弧长公式是解答本题的关键.
4、32
【分析】
根据圆内接四边形的性质得出∠ADB+∠ACB=180°,求出∠ADB=64°,根据C是弧AB的中点求出,根据圆周角定理得出∠BDC=∠ADC=ADB,再求出答案即可.
【详解】
解:∵A、C、B、D四点共圆,
∴∠ADB+∠ACB=180°,
∵∠ACB=116°,
∴∠ADB=180°﹣116°=64°,
∵C是弧AB的中点,
∴,
∴∠BDC=∠ADC=ADB=32°,
故答案为:32.
【点睛】
本题考查四点共圆性质,圆周角与弧的关系,掌握四点共圆性质,圆周角与弧的关系是解题关键.
5、
【分析】
先根据弧的度数与它所对应的圆心角的度数的关系,求得弧对应的圆心角的度数,再根据圆周角与圆心角的关系,则可求得.
【详解】
弧的度数等于它所对应的圆心角的度数,由于弧为,所以 ,
顶点在圆上且两边都和圆相交的角叫做圆周角,而一条弧所对的圆周角等于它所对的圆心角的一半,所以:
, ,
,
故答案为:.
【点睛】
本题考查弧、圆周角、圆心角的概念,及它们之间的关系,熟知同弧所对的圆周角等于圆心角的一半是解本题的关键.
三、解答题
1、
(1)图形见解析
(2)直径所对的圆周角是直角;三边相等的三角形是等边三角形.
【分析】
(1)根据要求作出图形即可;
(2)根据圆周角定理等边三角形的判定和性质解决问题即可.
(1)
如图,△ABC即为所求作.
(2)
∵AB为⊙O的直径,点C在⊙O上,
∴∠ACB=90°(直径所对的圆周角是直角),
连接OC.
∵OA=OC=AC,
∴△AOC为等边三角形(三边相等的三角形是等边三角形),
∴∠A=60°.
故答案为:直径所对的圆周角是直角,三边相等的三角形是等边三角形.
【点睛】
本题考查作图-复杂作图,等边三角形的判定和性质,圆周角定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
2、(1)图见解析;(2)直径所对的圆周角是直角,切线的判定定理
【分析】
(1)根据所给的几何语言作出对应的图形即可;
(2)根据圆周角定理和切线的判定定理解答即可.
【详解】
解:(1)补全图形如图所示,直线AP即为所求作;
(2)证明:连接BA,
由作法可知,
∴点A在以OP为直径的圆上,
∴(直径所对的圆周角是直角),
∵OA是的半径,
∴直线PA与相切(切线的判定定理),
故答案为:直径所对的圆周角是直角,切线的判定定理.
【点睛】
本题考查基本作图-画圆、圆周角定理、切线的判定定理,熟知复杂作图是在基本作图的基础上进行作图,一般是结合几何图形的性质,因此熟练掌握基本图形的性质和切线的判定是解答的关键.
3、(1)(4,2);(2)见解析;(3)
【分析】
(1)根据三角形的外接圆的圆心是三边垂直平分线的交点即可找到点P;
(2)根据位似中心与三角形三个顶点的连线将原三角形扩大2倍即可;
(3)根据直线和圆的位置关系:当半径大于或等于点A到BC的距离时,⊙A与线段BC有一个或两个公共点即可.
【详解】
解:如图所示:
(1)点P即为△ABC的外心,P点的坐标为(4,2),
故答案为:(4,2);
(2)图中画出的△A′B′C′即为所求作的图形;
(3)观察图形可知:r=时,⊙A与线段BC有一个公共点.
此时⊙A与线段BC相切,
当时,⊙A只经过点,
∴的取值范围是
故答案为:.
【点睛】
本题考查了作图 位似变换、三角形的外接圆与圆心、直线与圆的位置关系,解决本题的关键是根据位似中心画位似图形.
4、(1)见解析;(2)
【分析】
(1)先证明,再根据同圆中,等弧所对的圆周角相等即可证明;
(2)过O点作OE⊥BC于点E,连接OB,由垂径定理可得BE=CE=,由勾股定理求出,即可得到.
【详解】
解:(1)∵,
∴,
∴,
∴∠1=∠2;
(2)过O点作OE⊥BC于点E,连接OB,
∴BE=CE=,
∵AD为⊙O的直径,
∴OB=,
∴,
∴.
【点睛】
本题主要考查了垂径定理,勾股定理,同圆中等弧所对的圆周角相等,解题的关键在于能够熟练掌握圆的相关知识.
5、(1)答案见解析 (2)答案见解析
【分析】
(1)作线段BC的垂直平分线MN,交AB于点O,以O为圆心,OB为半径作⊙O 即可;
(2)连接OC,证明∠ACB= 120°,再证明∠ACO= 90°,即可得答案.
【详解】
解:(1)如下图,⊙O即为所作:
(2)证明:连接OC
∵△ABC中,∠A=∠B= 30°
∴∠ACB= 120°
由(1) 可知,OC= OB
∴∠OCB=∠B = 30°
∴∠ACO= 90°
∴AC是⊙O的相切.
【点睛】
本题考查作图-垂直平分线、圆的画法,等腰三角形的性质,切线的判定等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
