二次函数练习题(无答案)
图片预览
文档简介
二次函数练习题
1.抛物线y=-2(x+1)2+3的顶点坐标是___________
2.已知二次函数y=-x2+4x+5.用配方法化为顶点式为_____________,其最大值为_____________
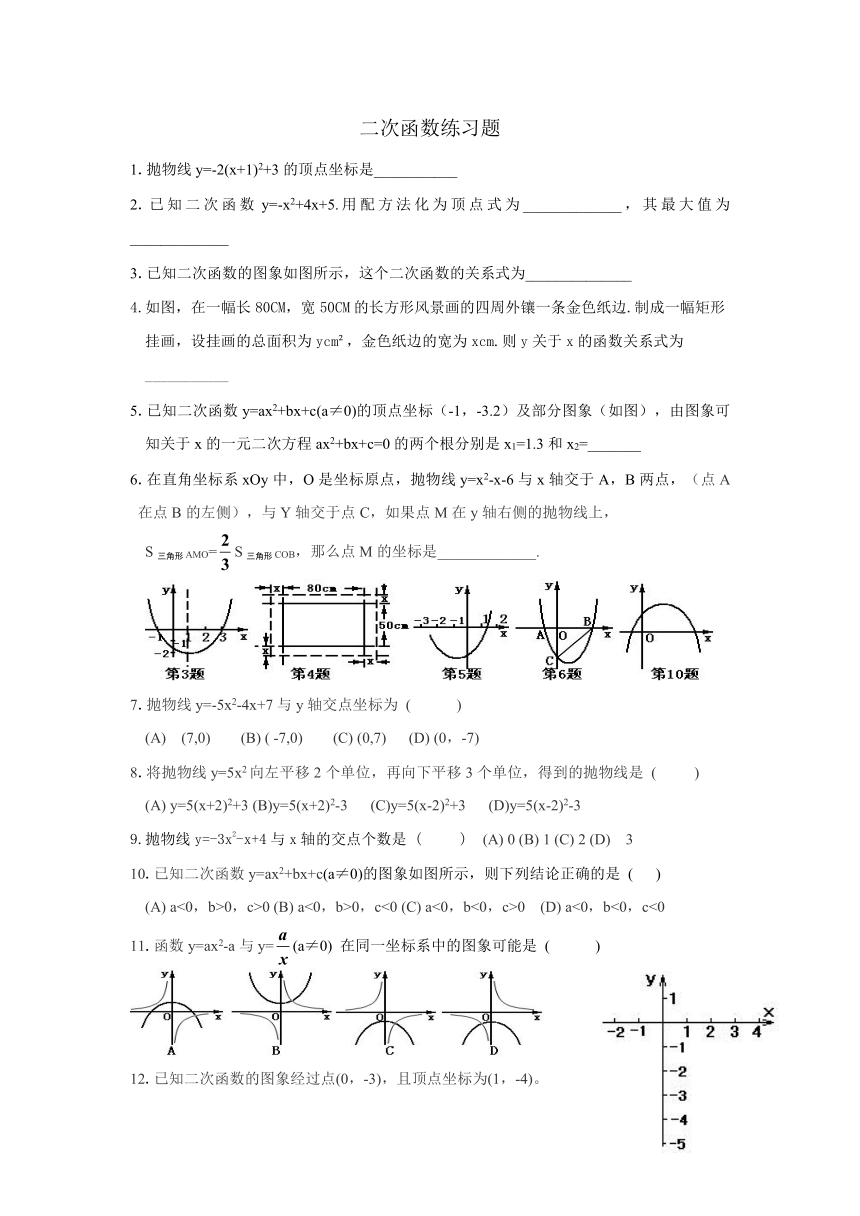
3.已知二次函数的图象如图所示,这个二次函数的关系式为______________
4.如图,在一幅长80CM,宽50CM的长方形风景画的四周外镶一条金色纸边.制成一幅矩形挂画,设挂画的总面积为ycm2,金色纸边的宽为xcm.则y关于x的函数关系式为___________
5.已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(-1,-3.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3和x2=_______
6.在直角坐标系xOy中,O是坐标原点,抛物线y=x2-x-6与x轴交于A,B两点,(点A在点B的左侧),与Y轴交于点C,如果点M在y轴右侧的抛物线上,
S三角形AMO=S三角形COB,那么点M的坐标是_____________.
7.抛物线y=-5x2-4x+7与y轴交点坐标为 ( )
(A) (7,0) (B) ( -7,0) (C) (0,7) (D) (0,-7)
8.将抛物线y=5x2向左平移2个单位,再向下平移3个单位,得到的抛物线是 ( )
(A) y=5(x+2)2+3 (B)y=5(x+2)2-3 (C)y=5(x-2)2+3 (D)y=5(x-2)2-3
9.抛物线y=-3x2-x+4与x轴的交点个数是 ( ) (A) 0 (B) 1 (C) 2 (D) 3
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是 ( )
(A) a<0,b>0,c>0 (B) a<0,b>0,c<0 (C) a<0,b<0,c>0 (D) a<0,b<0,c<0
11.函数y=ax2-a与y=(a≠0) 在同一坐标系中的图象可能是 ( )
12.已知二次函数的图象经过点(0,-3),且顶点坐标为(1,-4)。
(1) 求这个函数的关系式;
(2) 在直角坐标系中,画出它的图象.(图画在右边的坐标系中)
(3) 根据图象说明:当x为何值时,函数值为0?当x为何值时,函数y随着x的增大而增大?,当x为何值时,函数y随着x的增大而减小?
13.如图是抛物线拱桥,已知水位在AB位置时,水面宽4米,水位上升4米就达到警戒线CD,这时水面宽4米,若洪水到来时,水位每小时上升0. 5米.求水过警戒线后几小时淹到拱桥顶M处?
14.某商场将进货为30元的书包以40元售出,平均每月可售出600个,并且书包的售价每提高1元,月销售量就减少10个。
(1) 请写出每月售出书包的利润y(元)与每个书包涨价x(元)之间的函数关系式
(2) 设某月的利润为10 000 元,10 000元的利润是否为该月最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时书包的售价应定为多少元?
(3) 请分析并回答售价应定在什么范围内商家可获得利润。
15.已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(3,0),B(2,-3),C(0,-3)
(1) 求此抛物线的解析式和图象的对称轴;
(2) 在对称轴上是否存在一点P,使得ΔPAB中PA=PB?若存在,求出点P的坐标,若不存在,说明理由。
1.抛物线y=-2(x+1)2+3的顶点坐标是___________
2.已知二次函数y=-x2+4x+5.用配方法化为顶点式为_____________,其最大值为_____________
3.已知二次函数的图象如图所示,这个二次函数的关系式为______________
4.如图,在一幅长80CM,宽50CM的长方形风景画的四周外镶一条金色纸边.制成一幅矩形挂画,设挂画的总面积为ycm2,金色纸边的宽为xcm.则y关于x的函数关系式为___________
5.已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(-1,-3.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3和x2=_______
6.在直角坐标系xOy中,O是坐标原点,抛物线y=x2-x-6与x轴交于A,B两点,(点A在点B的左侧),与Y轴交于点C,如果点M在y轴右侧的抛物线上,
S三角形AMO=S三角形COB,那么点M的坐标是_____________.
7.抛物线y=-5x2-4x+7与y轴交点坐标为 ( )
(A) (7,0) (B) ( -7,0) (C) (0,7) (D) (0,-7)
8.将抛物线y=5x2向左平移2个单位,再向下平移3个单位,得到的抛物线是 ( )
(A) y=5(x+2)2+3 (B)y=5(x+2)2-3 (C)y=5(x-2)2+3 (D)y=5(x-2)2-3
9.抛物线y=-3x2-x+4与x轴的交点个数是 ( ) (A) 0 (B) 1 (C) 2 (D) 3
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是 ( )
(A) a<0,b>0,c>0 (B) a<0,b>0,c<0 (C) a<0,b<0,c>0 (D) a<0,b<0,c<0
11.函数y=ax2-a与y=(a≠0) 在同一坐标系中的图象可能是 ( )
12.已知二次函数的图象经过点(0,-3),且顶点坐标为(1,-4)。
(1) 求这个函数的关系式;
(2) 在直角坐标系中,画出它的图象.(图画在右边的坐标系中)
(3) 根据图象说明:当x为何值时,函数值为0?当x为何值时,函数y随着x的增大而增大?,当x为何值时,函数y随着x的增大而减小?
13.如图是抛物线拱桥,已知水位在AB位置时,水面宽4米,水位上升4米就达到警戒线CD,这时水面宽4米,若洪水到来时,水位每小时上升0. 5米.求水过警戒线后几小时淹到拱桥顶M处?
14.某商场将进货为30元的书包以40元售出,平均每月可售出600个,并且书包的售价每提高1元,月销售量就减少10个。
(1) 请写出每月售出书包的利润y(元)与每个书包涨价x(元)之间的函数关系式
(2) 设某月的利润为10 000 元,10 000元的利润是否为该月最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时书包的售价应定为多少元?
(3) 请分析并回答售价应定在什么范围内商家可获得利润。
15.已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(3,0),B(2,-3),C(0,-3)
(1) 求此抛物线的解析式和图象的对称轴;
(2) 在对称轴上是否存在一点P,使得ΔPAB中PA=PB?若存在,求出点P的坐标,若不存在,说明理由。
