小学数学 北师大版 六年级上册 一 圆 4 圆的周长1.5 圆周率的历史(35张ppt )
文档属性
| 名称 | 小学数学 北师大版 六年级上册 一 圆 4 圆的周长1.5 圆周率的历史(35张ppt ) |  | |
| 格式 | zip | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 15:31:59 | ||
图片预览









文档简介
(共35张PPT)
圆周率的历史
圆
1
什么叫圆周率?
圆的周长除以直径的商是一个固定的数,我们把它叫作圆周率。
圆周率,一般以π来表示,是一个在数学及物理学普遍存在的数学常数。它定义为圆形之周长与直径之比。
轮子是古代的重要发明,生活中也很常见。
一个轮子滚一圈可以滚多远?
轮子滚的距离与轮子的直径有没有关系呢?
(相当于圆的周长)
(它们的商是一个固定的数,称为圆周率)
显然轮子越大,滚得越远,那么滚的距离与轮子的直径之间有没有关系呢?
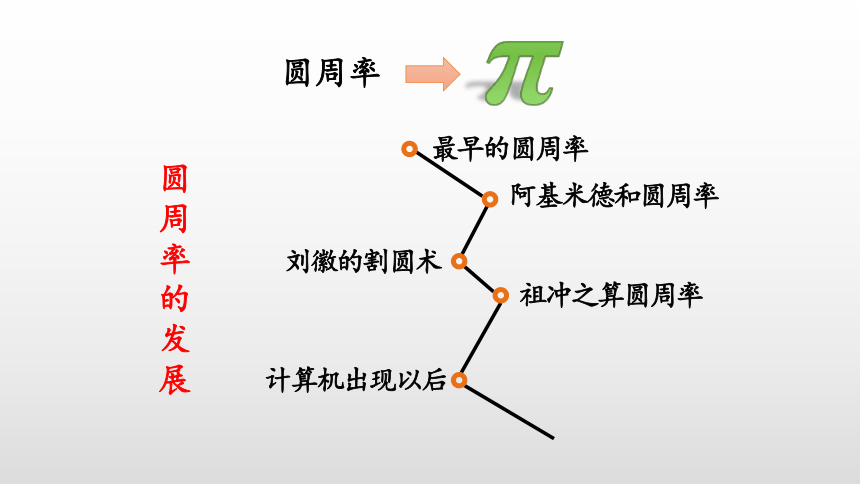
π
圆周率
圆
周
率
的
发
展
最早的圆周率
阿基米德和圆周率
刘徽的割圆术
祖冲之算圆周率
计算机出现以后
π
圆周率
最早的解决方案是测量。人类的祖先在实践中发现,不同粗细的圆木,用绳子绕上一圈,绳子的长度总是圆木
直径的3倍多一点。
在我国,现存有关圆周率的最早记载是2000多年前的《周髀算经》。
用测量的方法计算圆周率,圆周率的精确程度取决于测量的精确程度,而有许多实际困难限制了测量的精度。
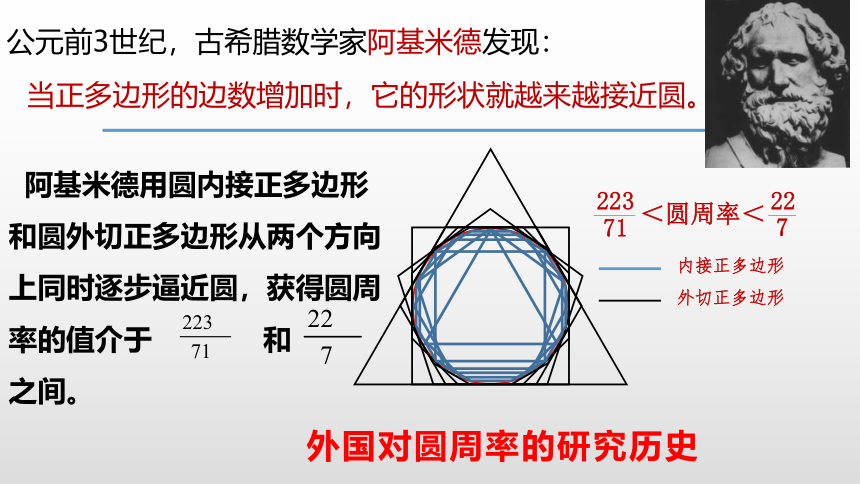
公元前3世纪,古希腊数学家阿基米德发现:
当正多边形的边数增加时,它的形状就越来越接近圆。
内接正多边形
外切正多边形
<圆周率<
71
7
22
223
阿基米德用圆内接正多边形和圆外切正多边形从两个方向上同时逐步逼近圆,获得圆周率的值介于 和 之间。
外国对圆周率的研究历史
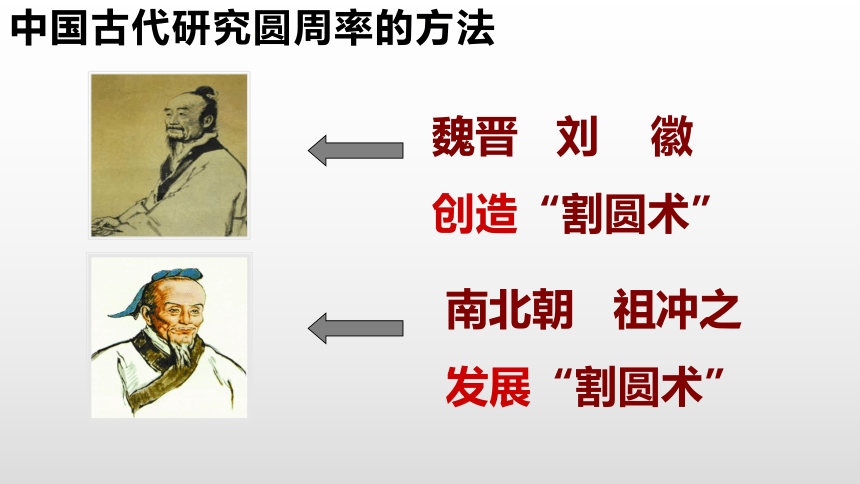
中国古代研究圆周率的方法
魏晋 刘 徽
创造“割圆术”
南北朝 祖冲之
发展“割圆术”
我国魏晋时期的数学家刘徽创造了用“割圆术”求圆周率的方法,在数学史上占有重要的地位。
刘徽用这样的方法不断地“割圆”,一直算到圆内接正192边形,得到圆周率的近似值是3.14.刘徽采用圆内接正多边形从一个方向逼近圆的方法来计算圆周率的。
刘徽的“割圆术”是怎样的呢?
我国南北朝时期的数学家祖冲之使用“缀术”计算圆周率。可惜这种方法早已失传。据专家推测,“缀术”类似“割圆术”,通过对正24576边形周长的计算来推导。计算相当繁杂,当时还没有算盘。
最后得出了π的两个分数形式的近似值:约率为,密率为,并且精确地算出圆周率在3.1415926和3.1415927之间。
祖冲之是世界上第一个计算圆周率精确到小数点后7位的人,比欧州人早了1000多年,这是多么了不起的贡献啊!
人 物 简 介
祖冲之(公元429年4月20日─公元500年)是我国杰出的数学家,科学家。南北朝时期人,汉族,字文远。祖冲之从小接受家传的科学知识。青年时进入华林学省,从事学术活动。其主要贡献在数学、天文历法和机械三方面。
祖冲之计算圆周率的故事
祖冲之采用刘徽“割圆术”(在圆内做正6边形,6边形的周长刚好是直径的3部,然后再做12边形、24边形……边数越多,它的周长就和圆的周长越接近)的方法算下去。在当时的情况下,不但没有计算机。也没有笔算,只能用小竹棍来计算。工作是艰巨的,这时祖冲之的儿子也能帮助他了。父子俩算了一天又一天,眼睛熬红了,人也渐渐瘦了下来。可大圆里的多边形却越画越多,3072边、6144边……边数越多,边长越短。父子俩蹲在地上,一个认真地画,一个细心地算,谁也不敢走神。
祖冲之计算圆周率的故事
最后,他们在那个大圆里画出了24576边形,并计算出它的周长是3.1415926。俩人看看摆在地上密密麻麻的小木棍,再看看画在地上的大圆的图形,高兴地笑了。后来,祖冲之推算出49152边形的周长不会超过3.1415927。所以他得出结论,圆周率是在3.1415926和3.1415927这两个数之间。
壹
肆
数学成就
完善历法
貳
机械制造方面
叁
天文历法方面
祖冲之的主要成就
为纪念这位伟大的古代科学家,人们将月球背面的一座环形山命名为“祖冲之环形山”,把小行星1888命名为“祖冲之小行星”。
数学家祖冲之在天文、历法、数学以及机械制造等方面的辉煌成就,充分表现了我国古代科学的高度发展水平。祖冲之之所以能够取得这样辉煌的成就,并不是偶然的。
首先,当时社会生产正在逐步发展,需要有一定的科学成就来配合前进,因而就推动了科学的进步,祖冲之就在这时候取得了天文、数学和机械制造等方面的成绩。
其次,从上古到这时候,在千百年的长期过程中已积累了不少科学成果,祖冲之就在前人创造的基础上做出了他的成绩。
至于祖冲之个人的认真学习,刻苦钻研,不迷信古人,不畏惧守旧势力,不怕斗争,不避艰难,自然也都是取得杰出成就的重要原因。
历
价
评
史
用正多边形逼近圆,计算量很大。随着数学及科技的不断发展,求圆周率的方法也日新月异。
电子计算机的出现带来了计算方面的革命,π的小数点后面的精确数字越来越多。
2000年,圆周率已经可以计算到小数点后12411亿位。
计算机时代
3.141592653589793238462643383279502884197169399375105820974944592307816062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989
你还知道了哪些有关圆周率的知识?
1736年以后开始用“π”表示圆周率。
我国对圆周率的研究历史
西汉 刘歆 3.15471
东汉 张 衡 3.1622
魏晋 刘 徽 3.14
南北朝 祖冲之 3.1415926(7)
几何法时期
卡西
中世纪晚期阿拉伯数学家、天文学家。主要表现在他所著的《算术之钥》、《圆周论》、《弦与正弦之书》等书之中。《圆周论》中的圆周率,是由圆内接正四边形算起,依次使边数加倍,准确到小数点后16位,打破了祖冲之(429~500)保持了近千年的7位小数准确的记录。
鲁道夫·范·科伊伦
(1540年—1610年),荷兰数学家。鲁道夫·科伊伦把他一生的大部分时间花在计算圆周率上。他运用的是1800年前阿基米德所适用的割圆法。他用2的六十二次方边形,将圆周率计算到小数点后第35位。他对自己的这个成就感到非常自豪,以致这个数被刻在他的墓碑上;直到今天,德国人还常常称这个数为“鲁道夫数”。
⊙1777年法国数学家浦丰利用“投针试验”求出圆周率。
⊙1844年达塞利用公式将圆周率的算到小数点后200位。
⊙1948年1月,弗格森和伦奇共同发表有808位正确小数的 π ,这是人工计算π的最高纪录。
分析法时期
电子计算机的出现使π值计算有了突飞猛进的发展。1949年,美国制造的世上首部电脑-ENIAC
Jean Guilloud和Martin Bouyer以电脑CDC 7600发现了π的第一百万个小数位。
1989年美国哥伦比亚大学研究人员用克雷-2型(Cray-2)和IBM-3090/VF型巨型电子计算机计算出π值小数点后4.8亿位数,后又继续算到小数点后10.1亿位数。
2010年1月7日——法国工程师法布里斯·贝拉将圆周率算到小数点后27000亿位。
2010年8月30日——日本计算机奇才近藤茂利用家用计算机和云计算相结合,计算出圆周率到小数点后5万亿位。
2011年10月16日,日本长野县饭田市公司职员近藤茂利用家中电脑将圆周率计算到小数点后10万亿位,刷新了2010年8月由他自己创下的5万亿位吉尼斯世界纪录。
计算机时代
课堂练习
1.看图填空(单位:cm)。
(1)
(2)
正方形的周长是( )cm,圆的周长是( )cm。
其中一个圆的周长是( )cm,长方形的周长是( )cm。
16
12.56
9.42
21
2.在一个周长为100cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是多少厘米?
100÷4÷2=12.5(厘米)
答:这个圆的半径是12.5厘米。
50×3.14÷2=78.5(cm)
50×4=200(cm)
200+78.5=278.5(cm)
278.5cm=2.785m
答:需要木条2.785m。
3.李明家一扇门上要装上形状如右图所示的装饰木条,需要木条多少米?
4.把圆柱形物体分别捆成如下图(从底面方向看)的形状,如果接头处不计,每组至少需要多长的绳子?你发现了什么?
第一幅图:7×2+3.14×7=35.98(cm)
第二幅图:7×4+3.14×7=49.98(cm)
第三幅图:7×8+3.14×7=77.98(cm)
这节课你们都学会了哪些知识?
课堂小结
圆周率π不仅与我们身边的数学紧密相连,更与我们的生活息息相关。
π≈3.14
圆周率的历史
圆
1
什么叫圆周率?
圆的周长除以直径的商是一个固定的数,我们把它叫作圆周率。
圆周率,一般以π来表示,是一个在数学及物理学普遍存在的数学常数。它定义为圆形之周长与直径之比。
轮子是古代的重要发明,生活中也很常见。
一个轮子滚一圈可以滚多远?
轮子滚的距离与轮子的直径有没有关系呢?
(相当于圆的周长)
(它们的商是一个固定的数,称为圆周率)
显然轮子越大,滚得越远,那么滚的距离与轮子的直径之间有没有关系呢?
π
圆周率
圆
周
率
的
发
展
最早的圆周率
阿基米德和圆周率
刘徽的割圆术
祖冲之算圆周率
计算机出现以后
π
圆周率
最早的解决方案是测量。人类的祖先在实践中发现,不同粗细的圆木,用绳子绕上一圈,绳子的长度总是圆木
直径的3倍多一点。
在我国,现存有关圆周率的最早记载是2000多年前的《周髀算经》。
用测量的方法计算圆周率,圆周率的精确程度取决于测量的精确程度,而有许多实际困难限制了测量的精度。
公元前3世纪,古希腊数学家阿基米德发现:
当正多边形的边数增加时,它的形状就越来越接近圆。
内接正多边形
外切正多边形
<圆周率<
71
7
22
223
阿基米德用圆内接正多边形和圆外切正多边形从两个方向上同时逐步逼近圆,获得圆周率的值介于 和 之间。
外国对圆周率的研究历史
中国古代研究圆周率的方法
魏晋 刘 徽
创造“割圆术”
南北朝 祖冲之
发展“割圆术”
我国魏晋时期的数学家刘徽创造了用“割圆术”求圆周率的方法,在数学史上占有重要的地位。
刘徽用这样的方法不断地“割圆”,一直算到圆内接正192边形,得到圆周率的近似值是3.14.刘徽采用圆内接正多边形从一个方向逼近圆的方法来计算圆周率的。
刘徽的“割圆术”是怎样的呢?
我国南北朝时期的数学家祖冲之使用“缀术”计算圆周率。可惜这种方法早已失传。据专家推测,“缀术”类似“割圆术”,通过对正24576边形周长的计算来推导。计算相当繁杂,当时还没有算盘。
最后得出了π的两个分数形式的近似值:约率为,密率为,并且精确地算出圆周率在3.1415926和3.1415927之间。
祖冲之是世界上第一个计算圆周率精确到小数点后7位的人,比欧州人早了1000多年,这是多么了不起的贡献啊!
人 物 简 介
祖冲之(公元429年4月20日─公元500年)是我国杰出的数学家,科学家。南北朝时期人,汉族,字文远。祖冲之从小接受家传的科学知识。青年时进入华林学省,从事学术活动。其主要贡献在数学、天文历法和机械三方面。
祖冲之计算圆周率的故事
祖冲之采用刘徽“割圆术”(在圆内做正6边形,6边形的周长刚好是直径的3部,然后再做12边形、24边形……边数越多,它的周长就和圆的周长越接近)的方法算下去。在当时的情况下,不但没有计算机。也没有笔算,只能用小竹棍来计算。工作是艰巨的,这时祖冲之的儿子也能帮助他了。父子俩算了一天又一天,眼睛熬红了,人也渐渐瘦了下来。可大圆里的多边形却越画越多,3072边、6144边……边数越多,边长越短。父子俩蹲在地上,一个认真地画,一个细心地算,谁也不敢走神。
祖冲之计算圆周率的故事
最后,他们在那个大圆里画出了24576边形,并计算出它的周长是3.1415926。俩人看看摆在地上密密麻麻的小木棍,再看看画在地上的大圆的图形,高兴地笑了。后来,祖冲之推算出49152边形的周长不会超过3.1415927。所以他得出结论,圆周率是在3.1415926和3.1415927这两个数之间。
壹
肆
数学成就
完善历法
貳
机械制造方面
叁
天文历法方面
祖冲之的主要成就
为纪念这位伟大的古代科学家,人们将月球背面的一座环形山命名为“祖冲之环形山”,把小行星1888命名为“祖冲之小行星”。
数学家祖冲之在天文、历法、数学以及机械制造等方面的辉煌成就,充分表现了我国古代科学的高度发展水平。祖冲之之所以能够取得这样辉煌的成就,并不是偶然的。
首先,当时社会生产正在逐步发展,需要有一定的科学成就来配合前进,因而就推动了科学的进步,祖冲之就在这时候取得了天文、数学和机械制造等方面的成绩。
其次,从上古到这时候,在千百年的长期过程中已积累了不少科学成果,祖冲之就在前人创造的基础上做出了他的成绩。
至于祖冲之个人的认真学习,刻苦钻研,不迷信古人,不畏惧守旧势力,不怕斗争,不避艰难,自然也都是取得杰出成就的重要原因。
历
价
评
史
用正多边形逼近圆,计算量很大。随着数学及科技的不断发展,求圆周率的方法也日新月异。
电子计算机的出现带来了计算方面的革命,π的小数点后面的精确数字越来越多。
2000年,圆周率已经可以计算到小数点后12411亿位。
计算机时代
3.141592653589793238462643383279502884197169399375105820974944592307816062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989
你还知道了哪些有关圆周率的知识?
1736年以后开始用“π”表示圆周率。
我国对圆周率的研究历史
西汉 刘歆 3.15471
东汉 张 衡 3.1622
魏晋 刘 徽 3.14
南北朝 祖冲之 3.1415926(7)
几何法时期
卡西
中世纪晚期阿拉伯数学家、天文学家。主要表现在他所著的《算术之钥》、《圆周论》、《弦与正弦之书》等书之中。《圆周论》中的圆周率,是由圆内接正四边形算起,依次使边数加倍,准确到小数点后16位,打破了祖冲之(429~500)保持了近千年的7位小数准确的记录。
鲁道夫·范·科伊伦
(1540年—1610年),荷兰数学家。鲁道夫·科伊伦把他一生的大部分时间花在计算圆周率上。他运用的是1800年前阿基米德所适用的割圆法。他用2的六十二次方边形,将圆周率计算到小数点后第35位。他对自己的这个成就感到非常自豪,以致这个数被刻在他的墓碑上;直到今天,德国人还常常称这个数为“鲁道夫数”。
⊙1777年法国数学家浦丰利用“投针试验”求出圆周率。
⊙1844年达塞利用公式将圆周率的算到小数点后200位。
⊙1948年1月,弗格森和伦奇共同发表有808位正确小数的 π ,这是人工计算π的最高纪录。
分析法时期
电子计算机的出现使π值计算有了突飞猛进的发展。1949年,美国制造的世上首部电脑-ENIAC
Jean Guilloud和Martin Bouyer以电脑CDC 7600发现了π的第一百万个小数位。
1989年美国哥伦比亚大学研究人员用克雷-2型(Cray-2)和IBM-3090/VF型巨型电子计算机计算出π值小数点后4.8亿位数,后又继续算到小数点后10.1亿位数。
2010年1月7日——法国工程师法布里斯·贝拉将圆周率算到小数点后27000亿位。
2010年8月30日——日本计算机奇才近藤茂利用家用计算机和云计算相结合,计算出圆周率到小数点后5万亿位。
2011年10月16日,日本长野县饭田市公司职员近藤茂利用家中电脑将圆周率计算到小数点后10万亿位,刷新了2010年8月由他自己创下的5万亿位吉尼斯世界纪录。
计算机时代
课堂练习
1.看图填空(单位:cm)。
(1)
(2)
正方形的周长是( )cm,圆的周长是( )cm。
其中一个圆的周长是( )cm,长方形的周长是( )cm。
16
12.56
9.42
21
2.在一个周长为100cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是多少厘米?
100÷4÷2=12.5(厘米)
答:这个圆的半径是12.5厘米。
50×3.14÷2=78.5(cm)
50×4=200(cm)
200+78.5=278.5(cm)
278.5cm=2.785m
答:需要木条2.785m。
3.李明家一扇门上要装上形状如右图所示的装饰木条,需要木条多少米?
4.把圆柱形物体分别捆成如下图(从底面方向看)的形状,如果接头处不计,每组至少需要多长的绳子?你发现了什么?
第一幅图:7×2+3.14×7=35.98(cm)
第二幅图:7×4+3.14×7=49.98(cm)
第三幅图:7×8+3.14×7=77.98(cm)
这节课你们都学会了哪些知识?
课堂小结
圆周率π不仅与我们身边的数学紧密相连,更与我们的生活息息相关。
π≈3.14
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
