苏科版七年级数学下册 12.2 证明 课前学习+课堂讲义教案
文档属性
| 名称 | 苏科版七年级数学下册 12.2 证明 课前学习+课堂讲义教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 13:50:05 | ||
图片预览

文档简介
12.2《证明》(第1课时)课前自主学习单
一、目标瞭望台
1.感受直观做出的判断不一定正确,体会证明的必要性。
2.能够运用我们已经掌握的知识,通过合情推理的方式证明一些规律、结论的正确性。
3.理解数学的严谨性,初步树立言之有理、落笔有据的推理意识,发展初步的演绎推理能力。
二、微课直播间
1.观察思考
探究1:看一看、量一量
(1)图1中三条线段a、b、c,线段 和线段d在同一直线上。
(2)观察图2直线AB和直线CD平行吗?
(3)在图3中,两条线段AB与CD,线段 更长一些。
(
(图1)
(图2)
(图3)
)
探究2:估一估,算一算
如图,如果用一根很长的钢缆沿赤道绕地球1周,然后把钢缆放长10米。(假设赤道长C米)这时钢缆与地球赤道之间的缝隙有多大 这个缝隙可以通过一头牛?还是一只老鼠?能说明你的估计是正确的吗?
(1)缝隙的宽度= ;
(2)这个缝隙可以通过 。
探究3:猜一猜,想一想
我们知道代数式的值与字母x的取值有关,x可以用任何数代入就可计算得到的值,既然x可以任意取值,那么代数式的值是不是也可以得到任何数值呢?如果不能,那么它的值有何特征呢?王亮同学通过计算,得到了下列结论:
(1)无论x取什么数,代数式的值总是偶数;
(2)无论x取什么数,代数式的值总是正数;
(3)无论x取什么数,代数式的值不是负数;
(4)无论x取什么数,代数式的值大于1。
你认为他的结论正确吗?为什么?
通过上面3个探究活动,谈谈你的体会:
。
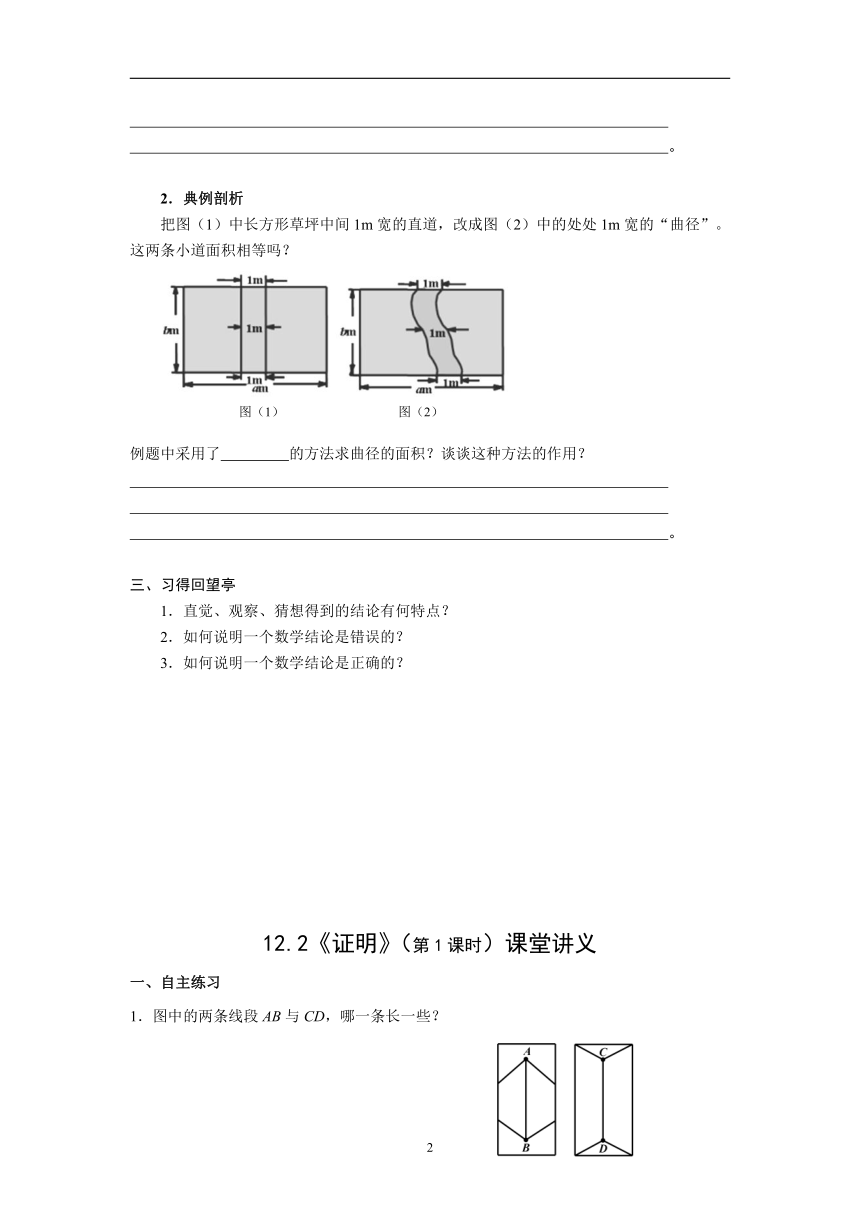
2.典例剖析
把图(1)中长方形草坪中间1m宽的直道,改成图(2)中的处处1m宽的“曲径”。这两条小道面积相等吗?
(
图(
1
)
图(
2
)
)
例题中采用了 的方法求曲径的面积?谈谈这种方法的作用?
。
三、习得回望亭
1.直觉、观察、猜想得到的结论有何特点?
2.如何说明一个数学结论是错误的?
3.如何说明一个数学结论是正确的?
12.2《证明》(第1课时)课堂讲义
一、自主练习
1.图中的两条线段AB与CD,哪一条长一些?
2.如图,两个大小相同的大圆,直径都为d,比较图(1)中10个小圆的周长之和与图(2)中2个小圆的周长之和,哪一个长?
图(1) 图(2)
3.当x=-3、0、2时,分别计算代数式A=与B=的值,并比较A、B值的大小:
(1)当x=-3时, A= ,B= ,A B;
当x= 0时, A= ,B= ,A B;
当x= 2时, A= ,B= ,A B;
(2)你换几个数再试试,你发现了什么?
二、挑战自我
如图(1),正方形ABCD的边长为a,正方形CEFG的边长为b,BC与CE、CD与CG在同一条直线上,连接BD、DF、BF,
(1)求出图中△BDF的面积。
(2)若正方形ABCD的边长保持不变,正方形CEFG的边长变为c(如图2),则△BDF的面积会不会发生变化?说明你的理由。
三、知识展望
如图,(1)画∠AOB=90°,并画∠AOB的角平分线OC.
(2)将三角尺的直角顶点落在OC的任意一点P上,使 三 角尺的两条直角边与
∠AOB的两边分别交于点E、F,并比较PE、PF的长度;
(3)把三角尺绕点P旋转,比较PE与PF的长度.
你能得到什么结论?
你的结论一定成立吗?
3
一、目标瞭望台
1.感受直观做出的判断不一定正确,体会证明的必要性。
2.能够运用我们已经掌握的知识,通过合情推理的方式证明一些规律、结论的正确性。
3.理解数学的严谨性,初步树立言之有理、落笔有据的推理意识,发展初步的演绎推理能力。
二、微课直播间
1.观察思考
探究1:看一看、量一量
(1)图1中三条线段a、b、c,线段 和线段d在同一直线上。
(2)观察图2直线AB和直线CD平行吗?
(3)在图3中,两条线段AB与CD,线段 更长一些。
(
(图1)
(图2)
(图3)
)
探究2:估一估,算一算
如图,如果用一根很长的钢缆沿赤道绕地球1周,然后把钢缆放长10米。(假设赤道长C米)这时钢缆与地球赤道之间的缝隙有多大 这个缝隙可以通过一头牛?还是一只老鼠?能说明你的估计是正确的吗?
(1)缝隙的宽度= ;
(2)这个缝隙可以通过 。
探究3:猜一猜,想一想
我们知道代数式的值与字母x的取值有关,x可以用任何数代入就可计算得到的值,既然x可以任意取值,那么代数式的值是不是也可以得到任何数值呢?如果不能,那么它的值有何特征呢?王亮同学通过计算,得到了下列结论:
(1)无论x取什么数,代数式的值总是偶数;
(2)无论x取什么数,代数式的值总是正数;
(3)无论x取什么数,代数式的值不是负数;
(4)无论x取什么数,代数式的值大于1。
你认为他的结论正确吗?为什么?
通过上面3个探究活动,谈谈你的体会:
。
2.典例剖析
把图(1)中长方形草坪中间1m宽的直道,改成图(2)中的处处1m宽的“曲径”。这两条小道面积相等吗?
(
图(
1
)
图(
2
)
)
例题中采用了 的方法求曲径的面积?谈谈这种方法的作用?
。
三、习得回望亭
1.直觉、观察、猜想得到的结论有何特点?
2.如何说明一个数学结论是错误的?
3.如何说明一个数学结论是正确的?
12.2《证明》(第1课时)课堂讲义
一、自主练习
1.图中的两条线段AB与CD,哪一条长一些?
2.如图,两个大小相同的大圆,直径都为d,比较图(1)中10个小圆的周长之和与图(2)中2个小圆的周长之和,哪一个长?
图(1) 图(2)
3.当x=-3、0、2时,分别计算代数式A=与B=的值,并比较A、B值的大小:
(1)当x=-3时, A= ,B= ,A B;
当x= 0时, A= ,B= ,A B;
当x= 2时, A= ,B= ,A B;
(2)你换几个数再试试,你发现了什么?
二、挑战自我
如图(1),正方形ABCD的边长为a,正方形CEFG的边长为b,BC与CE、CD与CG在同一条直线上,连接BD、DF、BF,
(1)求出图中△BDF的面积。
(2)若正方形ABCD的边长保持不变,正方形CEFG的边长变为c(如图2),则△BDF的面积会不会发生变化?说明你的理由。
三、知识展望
如图,(1)画∠AOB=90°,并画∠AOB的角平分线OC.
(2)将三角尺的直角顶点落在OC的任意一点P上,使 三 角尺的两条直角边与
∠AOB的两边分别交于点E、F,并比较PE、PF的长度;
(3)把三角尺绕点P旋转,比较PE与PF的长度.
你能得到什么结论?
你的结论一定成立吗?
3
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
