苏科版七年级数学下册 12.1 定义与命题 课件(共21张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 12.1 定义与命题 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 623.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 14:46:39 | ||
图片预览







文档简介
(共21张PPT)
12.1 定义与命题
情境引入
说一说生活中有哪些规范?
为了使我们的生活、生产有条不紊的进行,我们通常要有一些规定或规范。
因此在我们数学中,人们在说理时,常常需要使用一些名称和术语。
对名称或术语的含义进行描述或作出规定,
定义
如果没有这些规定与规范可以想象我们的生活将是怎样的
你能说一说生活中的规范吗?
请说出下列名词的定义:
(1)无理数 (2)直角三角形
(3)平行线 (4) 绝对值
(1)无限不循环小数是无理数.
(2)有一个角是直角的三角形是直角三角形.
(3)在同一平面内不相交的两条直线叫平行线
(4)数轴上表示一个数的点与原点的距离是一个数的绝对值
考考你
新知归纳:
定义有什么共同特征:
1.都是判断句。
2.都含有“是”“叫”或“为”这样的关键词
小组活动:
写出一个你熟悉的定义,组内交流,进行比较归纳,定义有什么共同的特征?
比较下列句子在表述形式上,哪些对事情作了判断?哪些没有对事情作出判断?
(1)鸟是动物.
(2)若a2=4,求a的值.
(3)若a2=b2,则a=b.
(4)a,b两条直线平行吗?
(5)画一个角等于已知角.
(6)0.33是无理数.
(7)两直线平行,同位角相等.
判 断:
(1)鸟是动物.
(3)若a2=b2,则a=b.
(6)0.33是无理数.
(7)两直线平行,同位角相等.
(1)鸟是动物.
(2)若a2=b2,则a=b.
(3)0.33是无理数.
(4)两直线平行,同位角相等.
一般地,对某一件事情作出正确或不正确的判断的句子叫做命题
共同特征:
陈述句子 有判断
新知归纳:
判断一个句子是不是命题的关键是什么?
1.表示判断的句子都是命题,而不管判断的结果是否正确
2.疑问句和命令性语句都不是命题
你能举出一些命题吗
2)两条直线相交,有且只有一个交点( )
4)一个平角的度数是180度( )
6)取线段AB的中点C;( )
1)长度相等的两条线段是相等的线段吗 ( )
7)画两条相等的线段( )
判断下列语句是不是命题?是用“Y”,不是用“N” 表示。
3)不相等的两个角不是对顶角( )
5)相等的两个角是对顶角( )
N
Y
N
N
Y
Y
Y
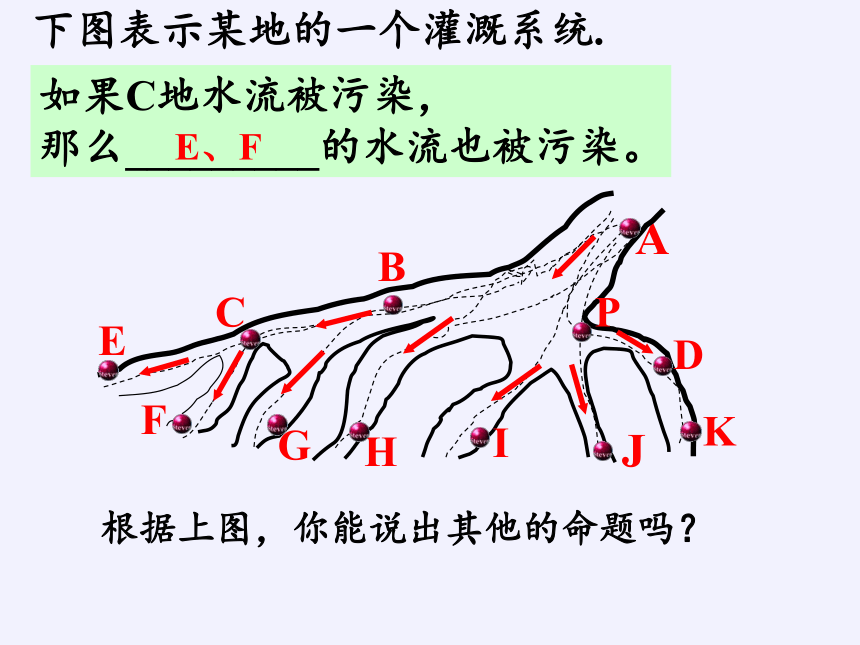
下图表示某地的一个灌溉系统.
A
B
C
E
F
H
G
D
K
I
J
如果C地水流被污染,
那么_________的水流也被污染。
E、F
根据上图,你能说出其他的命题吗?
P
命题: 两直线平行,同位角相等.
条件(题设)
结论
命题可看作由条件(condition)和结论(conclusion)
两部分组成,条件是已知事项,
结论是由已知事项推出的事项.
命题的结构
这样的命题可以写成”如果……那么……”的形式,其中“如果”开始的部分是条件,“那么”后面是结论.
如果两直线平行,那么同位角相等。
指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
⑴和为90°的两个角互为余角;
⑵三条边都相等的三角形是等边三角形;
⑶两直线平行,内错角相等。
典型例题
⑵三条边都相等的三角形是等边三角形;
条件是:
结论是:
改写成:
这个三角形是等边三角形
一个三角形的三条边都相等
如果一个三角形有三条边都相等,那么这个三角形是等边三角形。
⑶两直线平行,内错角相等;
条件是:
结论是:
改写成:
两条平行线被第三条直线所截
内错角相等
如果两条平行线被第三条直线所截,那么内错角相等。
⑴和为90°的两个角互为余角。
两个角的和为90°
这两个角互余
如果两个角的和为90°,那么这两个角互余。
解:
适当增加文字(条件),使语句通畅
条件是: ;
结论是: ;
改写成: .
(5)三角形的内角和等于180°;
(4)同角的余角相等;
⑶对顶角相等。
判断一个命题是假命题,只要举出一个满足命题条件,但结论不同于命题结论的例子就可以了。像这样的例子叫做
1.下列命题的条件是什么 结论是什么
(2)如果a>b,b>c,那么a>c;
(1)如果a,b两数的积为0,那么a,b两数都为0;
(3)如果两个角互为补角,那么这两个角的和是180度;
(4)相等的角是对顶角;
(5)对顶角相等.
2.上述的命题中,哪些是正确的 哪些是不正确的 你怎么知道
它们是不正确的 与同伴交流.
正确的命题称为真命题,不正确的的命题称为假命题.
趁热打铁
反例
小组活动:
写出一个命题,组内交流,并说出他的条件和结论,是真命题还是假命题
1.在数学运算中,除了加、减、乘、除等运算外,还可以定义新的运算。如定义一种“星”运算,“*”是它的运算符号,其运算法则是:
_____________;
请你参照以上方法,也定义一种新运算,
并给本组的同学做一做。
学以致用
____________
学以致用
2.观察下列方程,找出它们的共同特征,给出名称,并作出定义:
小组合作交流
这节课你有何收获,
能与大家分享、交流你的感受吗?
1、定义
对名称或术语的含义进行描述或作出规定,定义
2、命题:一般地,对某件事情作出正确或不正确的判断的句子叫做命题。
命题的结构是题设(已知条件)与结论(由已知条件推出的事项)。
谢 谢
12.1 定义与命题
情境引入
说一说生活中有哪些规范?
为了使我们的生活、生产有条不紊的进行,我们通常要有一些规定或规范。
因此在我们数学中,人们在说理时,常常需要使用一些名称和术语。
对名称或术语的含义进行描述或作出规定,
定义
如果没有这些规定与规范可以想象我们的生活将是怎样的
你能说一说生活中的规范吗?
请说出下列名词的定义:
(1)无理数 (2)直角三角形
(3)平行线 (4) 绝对值
(1)无限不循环小数是无理数.
(2)有一个角是直角的三角形是直角三角形.
(3)在同一平面内不相交的两条直线叫平行线
(4)数轴上表示一个数的点与原点的距离是一个数的绝对值
考考你
新知归纳:
定义有什么共同特征:
1.都是判断句。
2.都含有“是”“叫”或“为”这样的关键词
小组活动:
写出一个你熟悉的定义,组内交流,进行比较归纳,定义有什么共同的特征?
比较下列句子在表述形式上,哪些对事情作了判断?哪些没有对事情作出判断?
(1)鸟是动物.
(2)若a2=4,求a的值.
(3)若a2=b2,则a=b.
(4)a,b两条直线平行吗?
(5)画一个角等于已知角.
(6)0.33是无理数.
(7)两直线平行,同位角相等.
判 断:
(1)鸟是动物.
(3)若a2=b2,则a=b.
(6)0.33是无理数.
(7)两直线平行,同位角相等.
(1)鸟是动物.
(2)若a2=b2,则a=b.
(3)0.33是无理数.
(4)两直线平行,同位角相等.
一般地,对某一件事情作出正确或不正确的判断的句子叫做命题
共同特征:
陈述句子 有判断
新知归纳:
判断一个句子是不是命题的关键是什么?
1.表示判断的句子都是命题,而不管判断的结果是否正确
2.疑问句和命令性语句都不是命题
你能举出一些命题吗
2)两条直线相交,有且只有一个交点( )
4)一个平角的度数是180度( )
6)取线段AB的中点C;( )
1)长度相等的两条线段是相等的线段吗 ( )
7)画两条相等的线段( )
判断下列语句是不是命题?是用“Y”,不是用“N” 表示。
3)不相等的两个角不是对顶角( )
5)相等的两个角是对顶角( )
N
Y
N
N
Y
Y
Y
下图表示某地的一个灌溉系统.
A
B
C
E
F
H
G
D
K
I
J
如果C地水流被污染,
那么_________的水流也被污染。
E、F
根据上图,你能说出其他的命题吗?
P
命题: 两直线平行,同位角相等.
条件(题设)
结论
命题可看作由条件(condition)和结论(conclusion)
两部分组成,条件是已知事项,
结论是由已知事项推出的事项.
命题的结构
这样的命题可以写成”如果……那么……”的形式,其中“如果”开始的部分是条件,“那么”后面是结论.
如果两直线平行,那么同位角相等。
指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
⑴和为90°的两个角互为余角;
⑵三条边都相等的三角形是等边三角形;
⑶两直线平行,内错角相等。
典型例题
⑵三条边都相等的三角形是等边三角形;
条件是:
结论是:
改写成:
这个三角形是等边三角形
一个三角形的三条边都相等
如果一个三角形有三条边都相等,那么这个三角形是等边三角形。
⑶两直线平行,内错角相等;
条件是:
结论是:
改写成:
两条平行线被第三条直线所截
内错角相等
如果两条平行线被第三条直线所截,那么内错角相等。
⑴和为90°的两个角互为余角。
两个角的和为90°
这两个角互余
如果两个角的和为90°,那么这两个角互余。
解:
适当增加文字(条件),使语句通畅
条件是: ;
结论是: ;
改写成: .
(5)三角形的内角和等于180°;
(4)同角的余角相等;
⑶对顶角相等。
判断一个命题是假命题,只要举出一个满足命题条件,但结论不同于命题结论的例子就可以了。像这样的例子叫做
1.下列命题的条件是什么 结论是什么
(2)如果a>b,b>c,那么a>c;
(1)如果a,b两数的积为0,那么a,b两数都为0;
(3)如果两个角互为补角,那么这两个角的和是180度;
(4)相等的角是对顶角;
(5)对顶角相等.
2.上述的命题中,哪些是正确的 哪些是不正确的 你怎么知道
它们是不正确的 与同伴交流.
正确的命题称为真命题,不正确的的命题称为假命题.
趁热打铁
反例
小组活动:
写出一个命题,组内交流,并说出他的条件和结论,是真命题还是假命题
1.在数学运算中,除了加、减、乘、除等运算外,还可以定义新的运算。如定义一种“星”运算,“*”是它的运算符号,其运算法则是:
_____________;
请你参照以上方法,也定义一种新运算,
并给本组的同学做一做。
学以致用
____________
学以致用
2.观察下列方程,找出它们的共同特征,给出名称,并作出定义:
小组合作交流
这节课你有何收获,
能与大家分享、交流你的感受吗?
1、定义
对名称或术语的含义进行描述或作出规定,定义
2、命题:一般地,对某件事情作出正确或不正确的判断的句子叫做命题。
命题的结构是题设(已知条件)与结论(由已知条件推出的事项)。
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
