苏科版七年级数学下册 7.5多边形的内角和与外角和 课件(共19张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 7.5多边形的内角和与外角和 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
□
从三角形到多边形
生活数学
问题1:由下列图形你能抽象出什么几何图形?
长方形
(四边形)
五边形
四边形
六边形
…
n条边
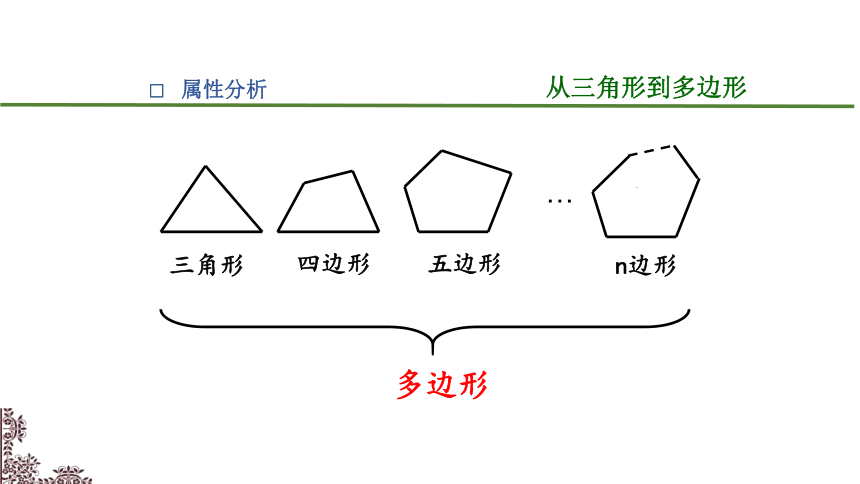
三角形
四边形
五边形
n边形
多边形
属性分析
□
从三角形到多边形
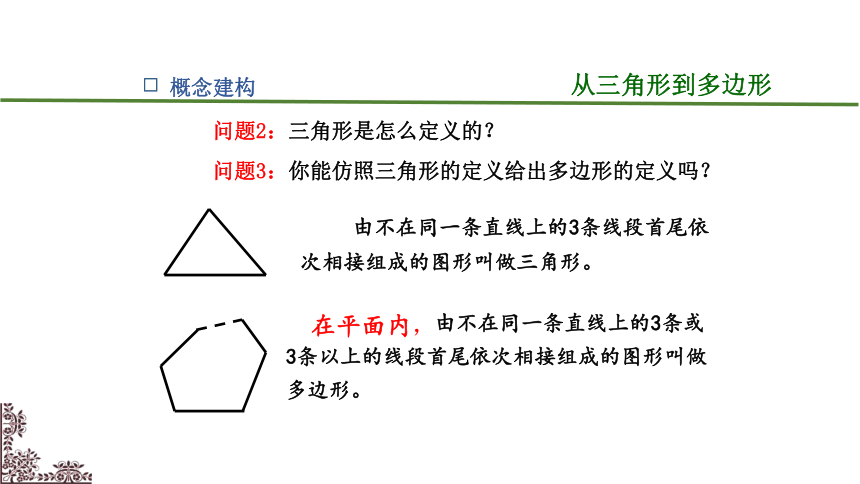
问题3:你能仿照三角形的定义给出多边形的定义吗?
由不在同一条直线上的3条线段首尾依次相接组成的图形叫做三角形。
由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形。
在平面内,
从三角形到多边形
□
概念建构
问题2:三角形是怎么定义的?
A
C
B
A
B
C
D
A
B
C
D
E
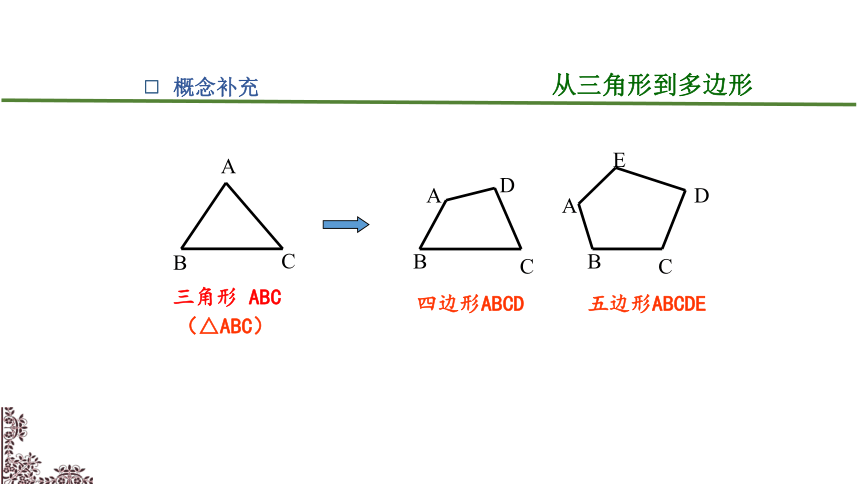
三角形 ABC
(△ABC)
四边形ABCD
五边形ABCDE
□
概念补充
从三角形到多边形
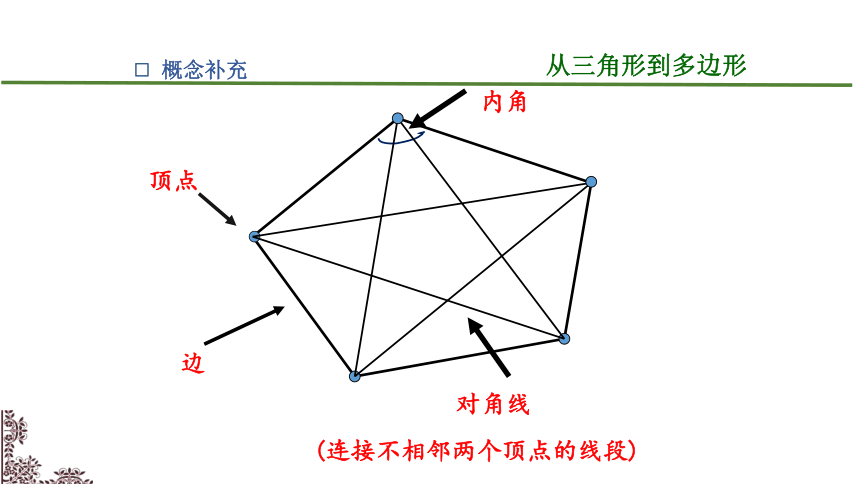
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
□
概念补充
从三角形到多边形
□
唤起经验
从三角形到多边形
问题4:学习了三角形概念后,我们是如何继续研究三角形的?
概念
性质
问题5:三角形的性质,我们是从哪些方面开展研究的?
三角形的组成元素:角和边
问题6:学习了多边形概念后,我们将如何继续研究多边形?
7.5 多边形的内角和与外角和(2)
义务教育教科书 (苏科版) 七年级 下册
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
……
扬州大学附属中学东部分校
柏素霞
□
唤起经验
探索四边形的内角和
问题1:三角形的内角和是多少度?
我们是怎么得来的?
小学:用度量、剪拼法发现
中学:用平行线的知识进行了说理
探索四边形的内角和
□
经验类比
问题2:你知道长方形的内角和是多少度吗?
问题3:你知道一般四边形的内角和是多少度吗?
A
B
C
D
转化
未知
已知
探索四边形的内角和
□
方法提炼
问题5:你最喜欢哪种转化方法?
复杂
简单
问题4:你还有其他转化方法吗?
3 4 5 6 7 … n
…
…
1
180°
探索n边形的内角和
□
归纳结论
多边形的边数
分成三角形的个数
多边形的内角和
……
边数增加1,内角和增加1800
已知内角和求边数
n边形的内角和等于(n-2)·180°
内角和一定是1800
的倍数
探索n边形的内角和
□
深化理解
……
问题6:对于n边形的内角和公式,
你有什么发现或思考吗?
解:设这个多边形为n边形,由题意可得:
(n-2)·180=1080
例1:一个多边形的内角和为1080°,这个多边形是几边形?
n=8
答:这个多边形为8边形.
多边形内角和的应用
□
学以致用
例2: 如图,在四边形ABCD中,如果∠A与∠C互补,
那么它的另一组对角∠B与∠D有什么关系?为什么?
因为 ∠A与∠C互补
所以 ∠A+∠C=180°
因为∠A+∠B+∠C+∠D=360°
所以∠B+∠D=180°
即∠B与∠D互补
解:∠B与∠D互补
如果四边形的一组对角互补,那么另一组对角也 .
互补
多边形内角和的应用
□
学以致用
D
A
B
C
拓展:如图,在四边形ABCD中,∠A与∠C互补,∠ABC、 ∠ADC的平分线分别交CD、AB于点E、F。 ∠1与∠2有怎样的数量关系?为什么?
□
学以致用
多边形内角和的应用
2、十边形的内角和是______度;
3、某六边形的内角都相等,则每个内角为____度;
问题1:选择与填空
1、一个多边形的内角和不可能是( )
A、1800° B、360° C、1000° D、900°
1440
120
4、(n+1)边形的内角和比n边形的内角和大____度。
C
180
多边形内角和的应用
□
练习巩固
问题2:求下列图形中x的值
140°
x°
x°
90°
2x°
150°
120°
x°
多边形内角和的应用
□
练习巩固
小结与思考
□
问题1:本节课的学习我们经历了怎样的过程?
问题2:在本节课中你获得了哪些学习方法?
你还有哪些困惑?
问题3:你能结合本课的学习提出一个问题吗?
总结提升
特殊
一般
推理
应用
已知
未知
类比
转化
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
1、阅读:课本p30-31 相关内容
2、必做:课本习题7.5
6、7、8
3、选做:撰写感悟小文章
□
学习延伸
课后作业
□
从三角形到多边形
生活数学
问题1:由下列图形你能抽象出什么几何图形?
长方形
(四边形)
五边形
四边形
六边形
…
n条边
三角形
四边形
五边形
n边形
多边形
属性分析
□
从三角形到多边形
问题3:你能仿照三角形的定义给出多边形的定义吗?
由不在同一条直线上的3条线段首尾依次相接组成的图形叫做三角形。
由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形。
在平面内,
从三角形到多边形
□
概念建构
问题2:三角形是怎么定义的?
A
C
B
A
B
C
D
A
B
C
D
E
三角形 ABC
(△ABC)
四边形ABCD
五边形ABCDE
□
概念补充
从三角形到多边形
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
□
概念补充
从三角形到多边形
□
唤起经验
从三角形到多边形
问题4:学习了三角形概念后,我们是如何继续研究三角形的?
概念
性质
问题5:三角形的性质,我们是从哪些方面开展研究的?
三角形的组成元素:角和边
问题6:学习了多边形概念后,我们将如何继续研究多边形?
7.5 多边形的内角和与外角和(2)
义务教育教科书 (苏科版) 七年级 下册
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
……
扬州大学附属中学东部分校
柏素霞
□
唤起经验
探索四边形的内角和
问题1:三角形的内角和是多少度?
我们是怎么得来的?
小学:用度量、剪拼法发现
中学:用平行线的知识进行了说理
探索四边形的内角和
□
经验类比
问题2:你知道长方形的内角和是多少度吗?
问题3:你知道一般四边形的内角和是多少度吗?
A
B
C
D
转化
未知
已知
探索四边形的内角和
□
方法提炼
问题5:你最喜欢哪种转化方法?
复杂
简单
问题4:你还有其他转化方法吗?
3 4 5 6 7 … n
…
…
1
180°
探索n边形的内角和
□
归纳结论
多边形的边数
分成三角形的个数
多边形的内角和
……
边数增加1,内角和增加1800
已知内角和求边数
n边形的内角和等于(n-2)·180°
内角和一定是1800
的倍数
探索n边形的内角和
□
深化理解
……
问题6:对于n边形的内角和公式,
你有什么发现或思考吗?
解:设这个多边形为n边形,由题意可得:
(n-2)·180=1080
例1:一个多边形的内角和为1080°,这个多边形是几边形?
n=8
答:这个多边形为8边形.
多边形内角和的应用
□
学以致用
例2: 如图,在四边形ABCD中,如果∠A与∠C互补,
那么它的另一组对角∠B与∠D有什么关系?为什么?
因为 ∠A与∠C互补
所以 ∠A+∠C=180°
因为∠A+∠B+∠C+∠D=360°
所以∠B+∠D=180°
即∠B与∠D互补
解:∠B与∠D互补
如果四边形的一组对角互补,那么另一组对角也 .
互补
多边形内角和的应用
□
学以致用
D
A
B
C
拓展:如图,在四边形ABCD中,∠A与∠C互补,∠ABC、 ∠ADC的平分线分别交CD、AB于点E、F。 ∠1与∠2有怎样的数量关系?为什么?
□
学以致用
多边形内角和的应用
2、十边形的内角和是______度;
3、某六边形的内角都相等,则每个内角为____度;
问题1:选择与填空
1、一个多边形的内角和不可能是( )
A、1800° B、360° C、1000° D、900°
1440
120
4、(n+1)边形的内角和比n边形的内角和大____度。
C
180
多边形内角和的应用
□
练习巩固
问题2:求下列图形中x的值
140°
x°
x°
90°
2x°
150°
120°
x°
多边形内角和的应用
□
练习巩固
小结与思考
□
问题1:本节课的学习我们经历了怎样的过程?
问题2:在本节课中你获得了哪些学习方法?
你还有哪些困惑?
问题3:你能结合本课的学习提出一个问题吗?
总结提升
特殊
一般
推理
应用
已知
未知
类比
转化
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
1、阅读:课本p30-31 相关内容
2、必做:课本习题7.5
6、7、8
3、选做:撰写感悟小文章
□
学习延伸
课后作业
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
