苏科版七年级数学下册 7.5 多边形的内角和与外角和 课件(共22张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 7.5 多边形的内角和与外角和 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 365.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
7.5 多边形的内角和与外角和
三角形蓝和三角形红见面了,蓝炫耀的说:“我的面积比你大,所以我的内角和也比你大!”红不服气的说:“那可不好说噢,你自己量量看!”
蓝用量角器量了量自己的内角和,就不再说话了!
同学们,你们知道其中的道理吗?
情境问题
想一想
三角形的三个内角和是1800
小学里我们用什么办法验证呢
方法:度量、剪拼图、折叠
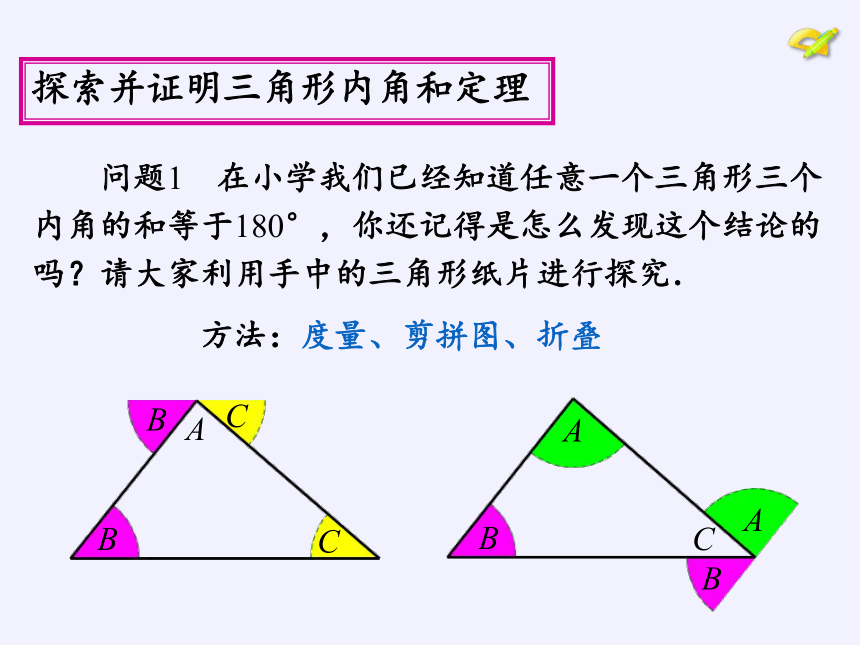
探索并证明三角形内角和定理
B
B
C
C
A
A
A
B
B
C
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
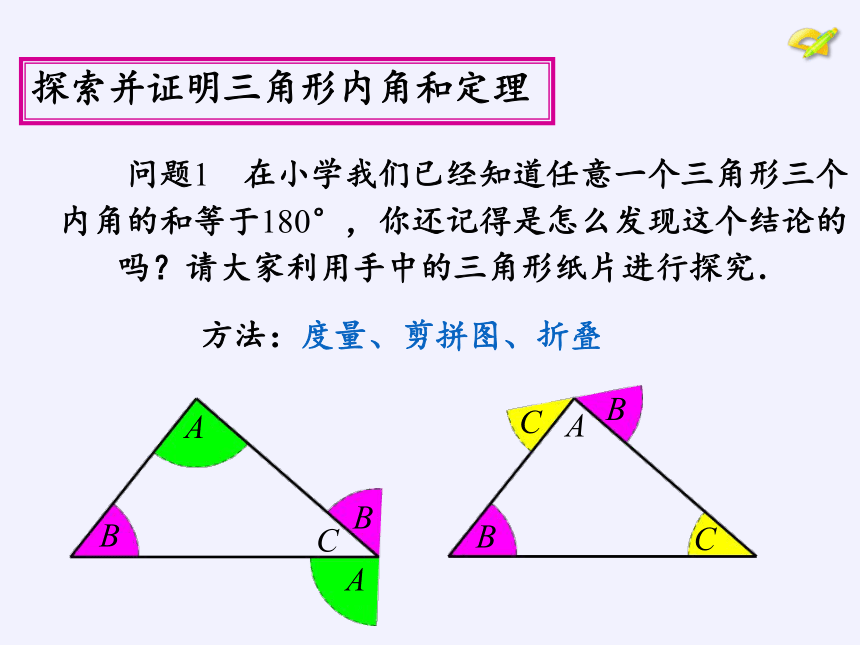
探索并证明三角形内角和定理
A
A
B
B
C
A
B
B
C
C
方法:度量、剪拼图、折叠
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
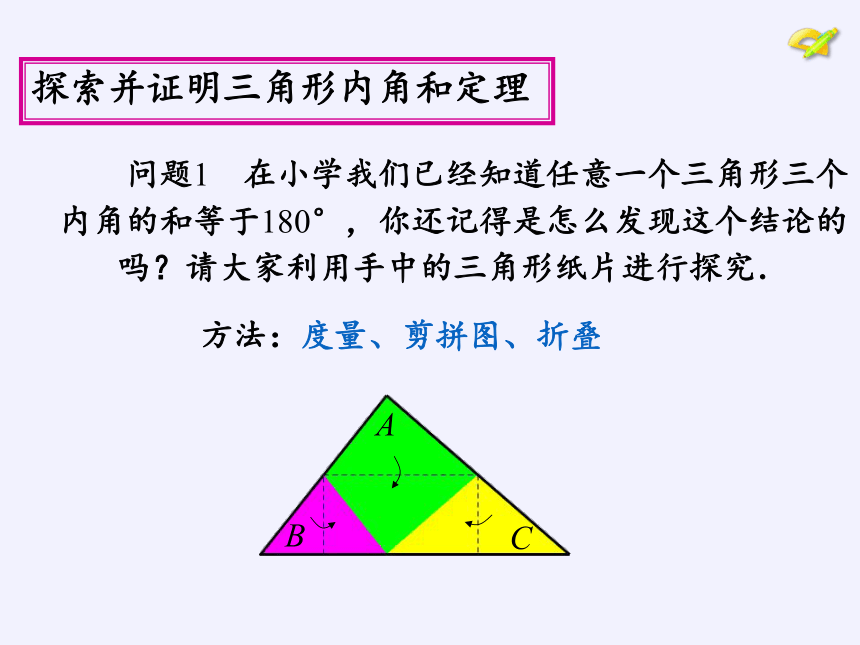
探索并证明三角形内角和定理
A
B
C
方法:度量、剪拼图、折叠
探索并证明三角形内角和定理
追问1 运用度量的方法,得出的三个内角的和都
是180°吗?为什么?
测量可能会有误差.
探索并证明三角形内角和定理
追问2 通过度量、剪拼图或折叠的方法验证了手
中的三角形纸片的三个内角和等于180°,但我们手中
的三角形只是所有三角形中有限的几个,而形状不同的
三角形有无数多个,我们如何能得出“所有的三角形的
三个内角的和都等于180°”这个结论呢?
需要通过推理的方法去证明.
探索并证明三角形内角和定理
问题2 你能从以上的操作过程中受到启发,想出
证明“三角形内角和等于180°”的方法吗?
探索并证明三角形内角和定理
追问1 在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A 的直线l,直线l 与边BC 有什么位置关系?
直线l 与边BC 平行.
B
B
C
C
A
l
探索并证明三角形内角和定理
追问2 在操作过程中,我们发现了与边BC 平行的
直线l,由此,你又能受到什么启发?你能发现证明
“三角形内角和等于180°”的思路吗?
通过添加与边BC
平行的辅助线l,利用
平行线的性质和平角
的定义即可证明结论.
B
B
C
C
A
l
证明:过点A 作直线l ,使l ∥BC.
∵ l ∥BC ,
∴ ∠2 = ∠4,
∠3 = ∠5
(两直线平行,内错角相等) .
探索并证明三角形内角和定理
追问3 结合下图,你能写出已知、求证和证明吗?
已知:△ABC.求证:∠A +∠B + ∠C = 180°.
A
B
C
2
4
1
5
3
l
探索并证明三角形内角和定理
追问3 结合下图,你能写出已知、求证和证明吗?
已知:△ABC.求证:∠A +∠B + ∠C = 180°.
A
B
C
2
4
1
5
3
l
证明:∵ ∠1 + ∠4 + ∠5 = 180°
(平角定义),
∴ ∠A + ∠B + ∠C = 180°
(等量代换).
三角形的内角和定理
三角形的3个内角的和等于180度。
1.根据下图填空:
(1)n= ; (2)x= ; (3)y= .
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27°
29°
59°
2.在直角△ABC中,∠C=90°,∠A+∠B= .
90°
总结:
直角三角形的两个锐角互余。
结论
1、在△ABC中,∠A=40°,∠B=∠C 求∠C的度数
2、已知在△ABC中,∠A+∠B=2∠C, 求∠C的度数.
3、已知在△ABC中,∠A:∠B:∠C=1:2:3,求最大内角的度数.
练一练
1、三角形的三个内角中,最多能有几个直角?最多能有几个钝角?
2、三角形的三个内角中,最多能有几个锐角?最少有几个锐角?
思考---回答
给你一个五角星,求∠A+∠B+∠C+∠D+∠E
拓展延伸
我有哪些收获呢?
与大家共分享!
学 而 不 思 则 罔
回头一看,我想说…
课 堂 小 结
(1)重点探究了三角形3个内角之间的关系.
三角形3个内角的和等于180°.
(2)由三角形3个内角之间的关系得到直
角三角形的一个性质:
直角三角形的两个锐角互余.
谢 谢
7.5 多边形的内角和与外角和
三角形蓝和三角形红见面了,蓝炫耀的说:“我的面积比你大,所以我的内角和也比你大!”红不服气的说:“那可不好说噢,你自己量量看!”
蓝用量角器量了量自己的内角和,就不再说话了!
同学们,你们知道其中的道理吗?
情境问题
想一想
三角形的三个内角和是1800
小学里我们用什么办法验证呢
方法:度量、剪拼图、折叠
探索并证明三角形内角和定理
B
B
C
C
A
A
A
B
B
C
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
探索并证明三角形内角和定理
A
A
B
B
C
A
B
B
C
C
方法:度量、剪拼图、折叠
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
探索并证明三角形内角和定理
A
B
C
方法:度量、剪拼图、折叠
探索并证明三角形内角和定理
追问1 运用度量的方法,得出的三个内角的和都
是180°吗?为什么?
测量可能会有误差.
探索并证明三角形内角和定理
追问2 通过度量、剪拼图或折叠的方法验证了手
中的三角形纸片的三个内角和等于180°,但我们手中
的三角形只是所有三角形中有限的几个,而形状不同的
三角形有无数多个,我们如何能得出“所有的三角形的
三个内角的和都等于180°”这个结论呢?
需要通过推理的方法去证明.
探索并证明三角形内角和定理
问题2 你能从以上的操作过程中受到启发,想出
证明“三角形内角和等于180°”的方法吗?
探索并证明三角形内角和定理
追问1 在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A 的直线l,直线l 与边BC 有什么位置关系?
直线l 与边BC 平行.
B
B
C
C
A
l
探索并证明三角形内角和定理
追问2 在操作过程中,我们发现了与边BC 平行的
直线l,由此,你又能受到什么启发?你能发现证明
“三角形内角和等于180°”的思路吗?
通过添加与边BC
平行的辅助线l,利用
平行线的性质和平角
的定义即可证明结论.
B
B
C
C
A
l
证明:过点A 作直线l ,使l ∥BC.
∵ l ∥BC ,
∴ ∠2 = ∠4,
∠3 = ∠5
(两直线平行,内错角相等) .
探索并证明三角形内角和定理
追问3 结合下图,你能写出已知、求证和证明吗?
已知:△ABC.求证:∠A +∠B + ∠C = 180°.
A
B
C
2
4
1
5
3
l
探索并证明三角形内角和定理
追问3 结合下图,你能写出已知、求证和证明吗?
已知:△ABC.求证:∠A +∠B + ∠C = 180°.
A
B
C
2
4
1
5
3
l
证明:∵ ∠1 + ∠4 + ∠5 = 180°
(平角定义),
∴ ∠A + ∠B + ∠C = 180°
(等量代换).
三角形的内角和定理
三角形的3个内角的和等于180度。
1.根据下图填空:
(1)n= ; (2)x= ; (3)y= .
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27°
29°
59°
2.在直角△ABC中,∠C=90°,∠A+∠B= .
90°
总结:
直角三角形的两个锐角互余。
结论
1、在△ABC中,∠A=40°,∠B=∠C 求∠C的度数
2、已知在△ABC中,∠A+∠B=2∠C, 求∠C的度数.
3、已知在△ABC中,∠A:∠B:∠C=1:2:3,求最大内角的度数.
练一练
1、三角形的三个内角中,最多能有几个直角?最多能有几个钝角?
2、三角形的三个内角中,最多能有几个锐角?最少有几个锐角?
思考---回答
给你一个五角星,求∠A+∠B+∠C+∠D+∠E
拓展延伸
我有哪些收获呢?
与大家共分享!
学 而 不 思 则 罔
回头一看,我想说…
课 堂 小 结
(1)重点探究了三角形3个内角之间的关系.
三角形3个内角的和等于180°.
(2)由三角形3个内角之间的关系得到直
角三角形的一个性质:
直角三角形的两个锐角互余.
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
