2021-2022学年人教版数学七年级下册5.2.2平行线的判定同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册5.2.2平行线的判定同步练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 315.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 13:46:18 | ||
图片预览



文档简介
平行线的判定
一、单选题
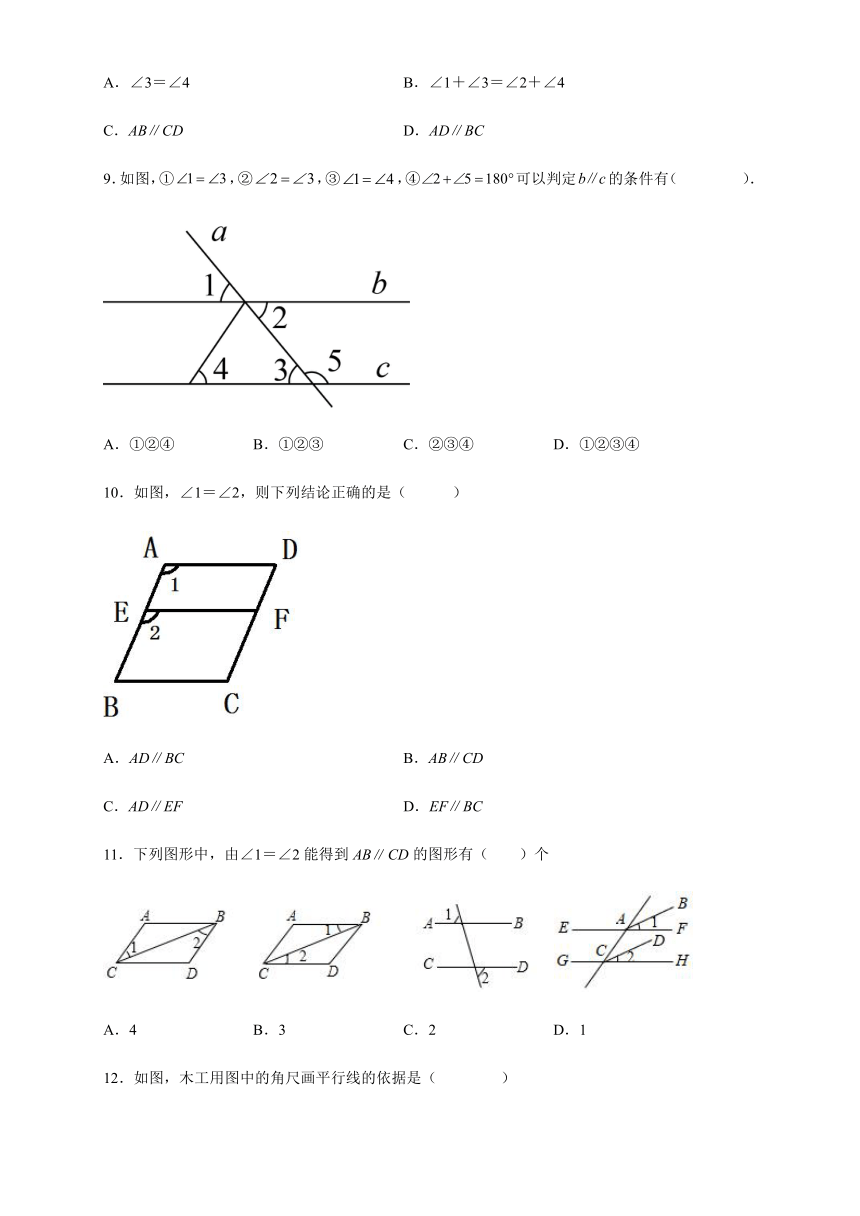
1.下列画出的直线a与b不一定平行的是( )
A. B.
C. D.
2.下列说法正确的是( )
A.同位角相等
B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角
D.在同一平面内,如果a∥b,b∥c,则a∥c
3.如图,直线a、b被直线c所截.若∠1=55°,则∠2的度数是( )时能判定a∥b.
A.35° B.45° C.125° D.145°
4.如图,直线a、b被直线c所截,下列选项中不一定能判定a∥b的是( )
A.∠1=∠3 B.∠1=∠4 C.∠2=∠4 D.∠2=∠5
5.如图是我们学过的用直尺和三角尺画平行线的方法示意图,其画图原理是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同旁内角互补
6.如图,和分别为直线与直线和相交所成角.如果,那么添加下列哪个条件后,可判定.( ).
A. B. C. D.
7.如图点E在BC的延长线上,则下列条件中,不能判定ABCD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
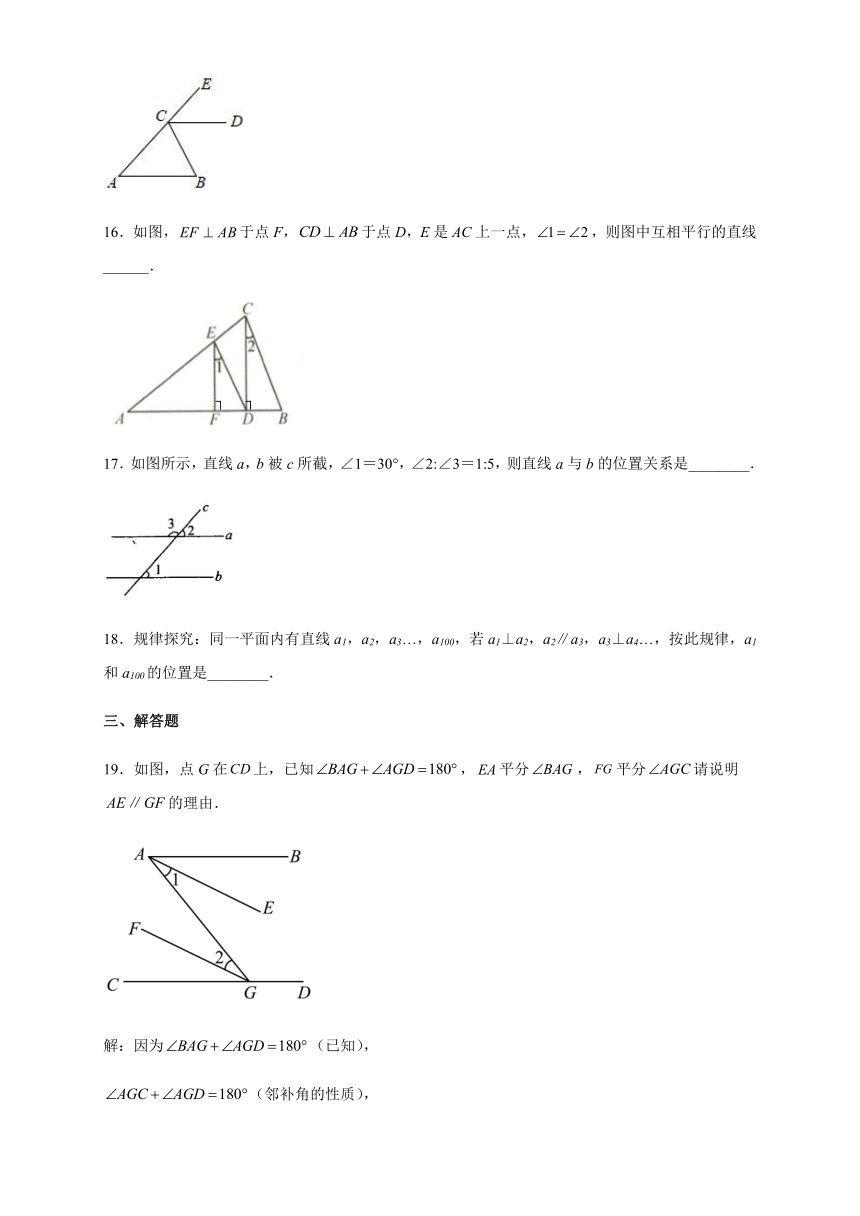
8.如图,∠1=∠2,由此推出的正确结论是( )
A.∠3=∠4 B.∠1+∠3=∠2+∠4
C.AB∥CD D.AD∥BC
9.如图,①,②,③,④可以判定的条件有( ).
A.①②④ B.①②③ C.②③④ D.①②③④
10.如图,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
11.下列图形中,由∠1=∠2能得到ABCD的图形有( )个
A.4 B.3 C.2 D.1
12.如图,木工用图中的角尺画平行线的依据是( )
A.垂直于同一条直线的两条直线平行
B.平行于同一条直线的两条直线平行
C.同位角相等,两直线平行
D.经过直线外一点,有且只有一条直线与这条直线平行
13.下列说法中正确的个数是( )
(1)在同一平面内,a、b、c是直线,a∥b,b∥c,则a∥c
(2)在同一平面内,a、b、c是直线,a⊥b,b⊥c,则a⊥c
(3)在同一平面内,a、b、c是直线,a∥b,a⊥c,则b⊥c
(4)在同一平面内,a、b、c是直线,a⊥b,b⊥c,则a∥c.
A.1 B.2 C.3 D.4
二、填空题
14.数学课上,老师要求同学们利用三角板画两条平行线.如图,小华的画法;①将含角三角尺的最长边与直线重合,用虚线作出一条最短边所在直线;②再次将含角三角尺的最短边与虚线重合,画出最长边所在直线,则.你认为他画图的依据是__.
15.如图A,C,E共线,请你添加一个条件,使ABCD,这个条件是______,你的依据是_____.
16.如图,于点F,于点D,E是AC上一点,,则图中互相平行的直线______.
17.如图所示,直线a,b被c所截,∠1=30°,∠2:∠3=1:5,则直线a与b的位置关系是________.
18.规律探究:同一平面内有直线a1,a2,a3…,a100,若a1⊥a2,a2∥a3,a3⊥a4…,按此规律,a1和a100的位置是________.
三、解答题
19.如图,点G在上,已知,平分,平分请说明的理由.
解:因为(已知),
(邻补角的性质),
所以(________________)
因为平分,
所以(________________).
因为平分,
所以______________,
得(等量代换),
所以_________________(________________).
20.如图,如果∠1=60°,∠2=120°,∠D=60°,那么AB与CD平行吗?BC与DE呢?
观察下面的解答过程,补充必要的依据或结论.
解∵∠1=60°(已知)
∠ABC=∠1 (① )
∴∠ABC=60°(等量代换)
又∵∠2=120°(已知)
∴(② )+∠2=180°(等式的性质)
∴AB∥CD (③ )
又∵∠2+∠BCD=(④ °)
∴∠BCD=60°(等式的性质)
∵∠D=60°(已知)
∴∠BCD=∠D (⑤ )
∴BC∥DE (⑥ )
21.如图,已知GH、MN分别平分∠AGE、∠DMF,且∠AGH=∠DMN,试说明ABCD的理由.
22.已知如图,∠ABC=∠ADC,BF、DE分别是∠ABC、∠ADC的角平分线,∠1=∠2,那么CD与AB平行吗 写出推理过程.
试卷第1页,共3页
参考答案:
1.A
解:A.直线a与b不一定平行,故本选项符合题意;
B.根据同旁内角互补,两直线平行可得a∥b,故本选项不符合题意;
C.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
D.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
故选:A.
2.D
解:A. 同位角不一定相等,故该项不符合题意;
B. 在同一平面内,如果a⊥b,b⊥c,则ac,故该项不符合题意;
C. 相等的角不一定是对顶角,故该项不符合题意;
D. 在同一平面内,如果ab,bc,则ac,故该项符合题意;
故选:D.
3.C
解:当∠1=∠3时,a∥b,
∴∠3=∠1=55°,
∵∠2+∠3=180°,
∴∠2=125°,
∴当∠2=125°时,a∥b,
故选:C.
4.B
解:A、,根据同位角相等,两直线平行能判定,此项不符题意;
B、,不一定能判定,此项符合题意;
C、,根据同位角相等,两直线平行能判定,此项不符题意;
D、,根据内错角相等,两直线平行能判定,此项不符题意;
故选:B.
5.A
如图,根据题意可知∠DPF=∠BAF,
∴(同位角相等,两直线平行).
故选A.
6.A
A.∵,∴∠3=180 -∠2=62 =∠1,∴能判定,此选项正确;
B.∵,∴∠3=180 -∠4=52 ≠∠1,∴不能判定,此选项错误;
C.∵,∴∠3≠∠1,∴不能判定,此选项错误;
D.∵,∴∠3=∠28 ≠∠1,∴不能判定,此选项错误;
故选:A
7.C
解:A、正确,符合“内错角相等,两条直线平行”的判定定理;
B、正确,符合“同位角相等,两条直线平行”的判定定理;
C、错误,若∠3=∠4,则AD∥BE;
D、正确,符合“同旁内角互补,两条直线平行”的判定定理;
故选:C.
8.C
解:∵∠1=∠2,
∴
故选C
9.A
解:①由于∠1和∠3是同位角,则①可判定;
②由于∠2和∠3是内错角,则②可判定;
③①由于∠1和∠4既不是同位角、也不是内错角,则③不能判定;
④①由于∠2和∠5是同旁内角,则④可判定;
即①②④可判定.
故选A.
10.C
解:略
11.C
解:第一个图形,∵∠1=∠2,
∴AC∥BD;故不符合题意;
第二个图形,∵∠1=∠2,
∴AB∥CD,故符合题意;
第三个图形,
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴AB∥CD;
第四个图形,∵∠1=∠2不能得到AB∥CD,
故不符合题意;
故选:C.
12.C
由于木工画一条线实际上是在画一个直角,且这些直角的一边在同一直线上,且这些直角是同位角相等,因而这些直线平行.
故选:C
13.C
在同一平面内,a、b、c是直线,a∥b,b∥c,则a∥c,故(1)正确;
在同一平面内,a、b、c是直线,a⊥b,b⊥c,则a∥c,故(2)错误;
在同一平面内,a、b、c是直线,a∥b,a⊥c,则b⊥c,故(3)正确;
在同一平面内,a、b、c是直线,a⊥b,b⊥c,则a∥c.故(4)正确;
综上所述,正确的是(1)(3)(4);
故选C.
14.内错角相等,两直线平行
解:画图的依据是内错角,相等两直线平行.
故答案为:内错角相等,两直线平行
15. ∠ECD=∠A 同位角相等,两直线平行(答案不唯一)
解:∵∠ECD=∠A,
∴AB∥CD(同位角相等,两直线平行)
故答案为:∠ECD=∠A;同位角相等,两直线平行(答案不唯一).
16.,
解: ,,
故答案为:
17.平行
解:∵∠2:∠3=1:5,
∴∠2=30°,
∴∠1=∠2,
∴a∥b,
故答案为:平行.
18.a1∥a100;
解:在同一平面内有直线两直线的位置,
关系是相交或平行,如图所示:
∵a1⊥a2,a2∥a3,
∴a1 ⊥a3,
又∵a3⊥a4,
∴a1∥a4,
又∵a4∥as,
∴a1∥a5,
又∵a5⊥a6,
∴a1⊥a6,
又∵a6∥a7,
∴a1⊥a7,
…
从以上的规律可知:a1与an的位置关系是4为周期进行循环,
若下角标的余数为0或1时与a1平行;若下角标的余数为2或3时与a1垂直.
∵100=4×25,
∴a1∥a100,
故答案为:a1∥a100.
19.同角的补角相等,角平分线的定义,∠AGC,,内错角相等两直线平行
解:因为(已知),
(邻补角的性质),
所以(同角的补角相等)
因为平分,
所以(角平分线的定义).
因为平分,
所以∠AGC,
得(等量代换),
所以(内错角相等两直线平行),
故答案为:同角的补角相等,角平分线的定义,∠AGC,,内错角相等两直线平行.
20.对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
解∵∠1=60°(已知)
∠ABC=∠1 (对顶角相等),
∴∠ABC=60°(等量代换),
又∵∠2=120°(已知),
∴∠ABC+∠2=180°(等式的性质),
∴AB∥CD (同旁内角互补,两直线平行),
又∵∠2+∠BCD=180°,
∴∠BCD=60°(等式的性质),
∵∠D=60°(已知),
∴∠BCD=∠D (等量代换),
∴BC∥DE (内错角相等,两直线平行),
故答案为:对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
21.见解析
∵GH平分∠AGE,
∴∠AGE=2∠AGH
同理∠DMF=2∠DMN
∵∠AGH=∠DMN
∴∠AGE=∠DMF
又∵∠AGE=∠FGB
∴∠DMF=∠FGB
∴ABCD (同位角相等,两直线平行).
22.平行,见解析
解:CD∥AB.理由如下:
∵BF、DE分别是∠ABC、∠ADC的角平分线,
∴∠3=∠ADC,∠2=∠ABC.
∵∠ABC=∠ADC,
∴∠3=∠2.
又∵∠1=∠2,
∴∠3=∠1.
∴CD∥AB(内错角相等,两直线平行).
答案第1页,共2页
一、单选题
1.下列画出的直线a与b不一定平行的是( )
A. B.
C. D.
2.下列说法正确的是( )
A.同位角相等
B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角
D.在同一平面内,如果a∥b,b∥c,则a∥c
3.如图,直线a、b被直线c所截.若∠1=55°,则∠2的度数是( )时能判定a∥b.
A.35° B.45° C.125° D.145°
4.如图,直线a、b被直线c所截,下列选项中不一定能判定a∥b的是( )
A.∠1=∠3 B.∠1=∠4 C.∠2=∠4 D.∠2=∠5
5.如图是我们学过的用直尺和三角尺画平行线的方法示意图,其画图原理是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同旁内角互补
6.如图,和分别为直线与直线和相交所成角.如果,那么添加下列哪个条件后,可判定.( ).
A. B. C. D.
7.如图点E在BC的延长线上,则下列条件中,不能判定ABCD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
8.如图,∠1=∠2,由此推出的正确结论是( )
A.∠3=∠4 B.∠1+∠3=∠2+∠4
C.AB∥CD D.AD∥BC
9.如图,①,②,③,④可以判定的条件有( ).
A.①②④ B.①②③ C.②③④ D.①②③④
10.如图,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
11.下列图形中,由∠1=∠2能得到ABCD的图形有( )个
A.4 B.3 C.2 D.1
12.如图,木工用图中的角尺画平行线的依据是( )
A.垂直于同一条直线的两条直线平行
B.平行于同一条直线的两条直线平行
C.同位角相等,两直线平行
D.经过直线外一点,有且只有一条直线与这条直线平行
13.下列说法中正确的个数是( )
(1)在同一平面内,a、b、c是直线,a∥b,b∥c,则a∥c
(2)在同一平面内,a、b、c是直线,a⊥b,b⊥c,则a⊥c
(3)在同一平面内,a、b、c是直线,a∥b,a⊥c,则b⊥c
(4)在同一平面内,a、b、c是直线,a⊥b,b⊥c,则a∥c.
A.1 B.2 C.3 D.4
二、填空题
14.数学课上,老师要求同学们利用三角板画两条平行线.如图,小华的画法;①将含角三角尺的最长边与直线重合,用虚线作出一条最短边所在直线;②再次将含角三角尺的最短边与虚线重合,画出最长边所在直线,则.你认为他画图的依据是__.
15.如图A,C,E共线,请你添加一个条件,使ABCD,这个条件是______,你的依据是_____.
16.如图,于点F,于点D,E是AC上一点,,则图中互相平行的直线______.
17.如图所示,直线a,b被c所截,∠1=30°,∠2:∠3=1:5,则直线a与b的位置关系是________.
18.规律探究:同一平面内有直线a1,a2,a3…,a100,若a1⊥a2,a2∥a3,a3⊥a4…,按此规律,a1和a100的位置是________.
三、解答题
19.如图,点G在上,已知,平分,平分请说明的理由.
解:因为(已知),
(邻补角的性质),
所以(________________)
因为平分,
所以(________________).
因为平分,
所以______________,
得(等量代换),
所以_________________(________________).
20.如图,如果∠1=60°,∠2=120°,∠D=60°,那么AB与CD平行吗?BC与DE呢?
观察下面的解答过程,补充必要的依据或结论.
解∵∠1=60°(已知)
∠ABC=∠1 (① )
∴∠ABC=60°(等量代换)
又∵∠2=120°(已知)
∴(② )+∠2=180°(等式的性质)
∴AB∥CD (③ )
又∵∠2+∠BCD=(④ °)
∴∠BCD=60°(等式的性质)
∵∠D=60°(已知)
∴∠BCD=∠D (⑤ )
∴BC∥DE (⑥ )
21.如图,已知GH、MN分别平分∠AGE、∠DMF,且∠AGH=∠DMN,试说明ABCD的理由.
22.已知如图,∠ABC=∠ADC,BF、DE分别是∠ABC、∠ADC的角平分线,∠1=∠2,那么CD与AB平行吗 写出推理过程.
试卷第1页,共3页
参考答案:
1.A
解:A.直线a与b不一定平行,故本选项符合题意;
B.根据同旁内角互补,两直线平行可得a∥b,故本选项不符合题意;
C.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
D.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
故选:A.
2.D
解:A. 同位角不一定相等,故该项不符合题意;
B. 在同一平面内,如果a⊥b,b⊥c,则ac,故该项不符合题意;
C. 相等的角不一定是对顶角,故该项不符合题意;
D. 在同一平面内,如果ab,bc,则ac,故该项符合题意;
故选:D.
3.C
解:当∠1=∠3时,a∥b,
∴∠3=∠1=55°,
∵∠2+∠3=180°,
∴∠2=125°,
∴当∠2=125°时,a∥b,
故选:C.
4.B
解:A、,根据同位角相等,两直线平行能判定,此项不符题意;
B、,不一定能判定,此项符合题意;
C、,根据同位角相等,两直线平行能判定,此项不符题意;
D、,根据内错角相等,两直线平行能判定,此项不符题意;
故选:B.
5.A
如图,根据题意可知∠DPF=∠BAF,
∴(同位角相等,两直线平行).
故选A.
6.A
A.∵,∴∠3=180 -∠2=62 =∠1,∴能判定,此选项正确;
B.∵,∴∠3=180 -∠4=52 ≠∠1,∴不能判定,此选项错误;
C.∵,∴∠3≠∠1,∴不能判定,此选项错误;
D.∵,∴∠3=∠28 ≠∠1,∴不能判定,此选项错误;
故选:A
7.C
解:A、正确,符合“内错角相等,两条直线平行”的判定定理;
B、正确,符合“同位角相等,两条直线平行”的判定定理;
C、错误,若∠3=∠4,则AD∥BE;
D、正确,符合“同旁内角互补,两条直线平行”的判定定理;
故选:C.
8.C
解:∵∠1=∠2,
∴
故选C
9.A
解:①由于∠1和∠3是同位角,则①可判定;
②由于∠2和∠3是内错角,则②可判定;
③①由于∠1和∠4既不是同位角、也不是内错角,则③不能判定;
④①由于∠2和∠5是同旁内角,则④可判定;
即①②④可判定.
故选A.
10.C
解:略
11.C
解:第一个图形,∵∠1=∠2,
∴AC∥BD;故不符合题意;
第二个图形,∵∠1=∠2,
∴AB∥CD,故符合题意;
第三个图形,
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴AB∥CD;
第四个图形,∵∠1=∠2不能得到AB∥CD,
故不符合题意;
故选:C.
12.C
由于木工画一条线实际上是在画一个直角,且这些直角的一边在同一直线上,且这些直角是同位角相等,因而这些直线平行.
故选:C
13.C
在同一平面内,a、b、c是直线,a∥b,b∥c,则a∥c,故(1)正确;
在同一平面内,a、b、c是直线,a⊥b,b⊥c,则a∥c,故(2)错误;
在同一平面内,a、b、c是直线,a∥b,a⊥c,则b⊥c,故(3)正确;
在同一平面内,a、b、c是直线,a⊥b,b⊥c,则a∥c.故(4)正确;
综上所述,正确的是(1)(3)(4);
故选C.
14.内错角相等,两直线平行
解:画图的依据是内错角,相等两直线平行.
故答案为:内错角相等,两直线平行
15. ∠ECD=∠A 同位角相等,两直线平行(答案不唯一)
解:∵∠ECD=∠A,
∴AB∥CD(同位角相等,两直线平行)
故答案为:∠ECD=∠A;同位角相等,两直线平行(答案不唯一).
16.,
解: ,,
故答案为:
17.平行
解:∵∠2:∠3=1:5,
∴∠2=30°,
∴∠1=∠2,
∴a∥b,
故答案为:平行.
18.a1∥a100;
解:在同一平面内有直线两直线的位置,
关系是相交或平行,如图所示:
∵a1⊥a2,a2∥a3,
∴a1 ⊥a3,
又∵a3⊥a4,
∴a1∥a4,
又∵a4∥as,
∴a1∥a5,
又∵a5⊥a6,
∴a1⊥a6,
又∵a6∥a7,
∴a1⊥a7,
…
从以上的规律可知:a1与an的位置关系是4为周期进行循环,
若下角标的余数为0或1时与a1平行;若下角标的余数为2或3时与a1垂直.
∵100=4×25,
∴a1∥a100,
故答案为:a1∥a100.
19.同角的补角相等,角平分线的定义,∠AGC,,内错角相等两直线平行
解:因为(已知),
(邻补角的性质),
所以(同角的补角相等)
因为平分,
所以(角平分线的定义).
因为平分,
所以∠AGC,
得(等量代换),
所以(内错角相等两直线平行),
故答案为:同角的补角相等,角平分线的定义,∠AGC,,内错角相等两直线平行.
20.对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
解∵∠1=60°(已知)
∠ABC=∠1 (对顶角相等),
∴∠ABC=60°(等量代换),
又∵∠2=120°(已知),
∴∠ABC+∠2=180°(等式的性质),
∴AB∥CD (同旁内角互补,两直线平行),
又∵∠2+∠BCD=180°,
∴∠BCD=60°(等式的性质),
∵∠D=60°(已知),
∴∠BCD=∠D (等量代换),
∴BC∥DE (内错角相等,两直线平行),
故答案为:对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
21.见解析
∵GH平分∠AGE,
∴∠AGE=2∠AGH
同理∠DMF=2∠DMN
∵∠AGH=∠DMN
∴∠AGE=∠DMF
又∵∠AGE=∠FGB
∴∠DMF=∠FGB
∴ABCD (同位角相等,两直线平行).
22.平行,见解析
解:CD∥AB.理由如下:
∵BF、DE分别是∠ABC、∠ADC的角平分线,
∴∠3=∠ADC,∠2=∠ABC.
∵∠ABC=∠ADC,
∴∠3=∠2.
又∵∠1=∠2,
∴∠3=∠1.
∴CD∥AB(内错角相等,两直线平行).
答案第1页,共2页
