苏科版七年级数学下册 7.5 多边形的内角和与外角和 课件(共18张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 7.5 多边形的内角和与外角和 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 474.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
7.5 多边形的内角和与外角和
2、能运用三角形内角和定理进行有关的说理与计算.
学习目标
1、探索三角形三个内角之间的关系.
内角三兄弟之争
在一个直角三角形里住着三个内角兄弟,
平时三兄弟非常团结。可是有一天,老二
突然不高兴,发起脾气来,它指着老大直角
说:“你凭什么度数最大,我也要和你一样大!”
老大说:“不行呀,这是不可能的,否则,
我们这个家就再也围不起来了…”
“为什么?”老二很纳闷。
同学们,你们知道其中的道理吗?
一、情境创设
想一想
三角形的3个内角和是1800
小学里我们用什么方法验证呢
方法一: 度量
请每位同学在试卷上任意画一个三角形,用量角器量出各内角的度数,并求它们的和.
方法二:拼图
将三角形纸片的3个内角撕开,然后拼在一起,观察它们的和是否为180
你还有其他方法进行验证吗
1
2
a
b
A
B
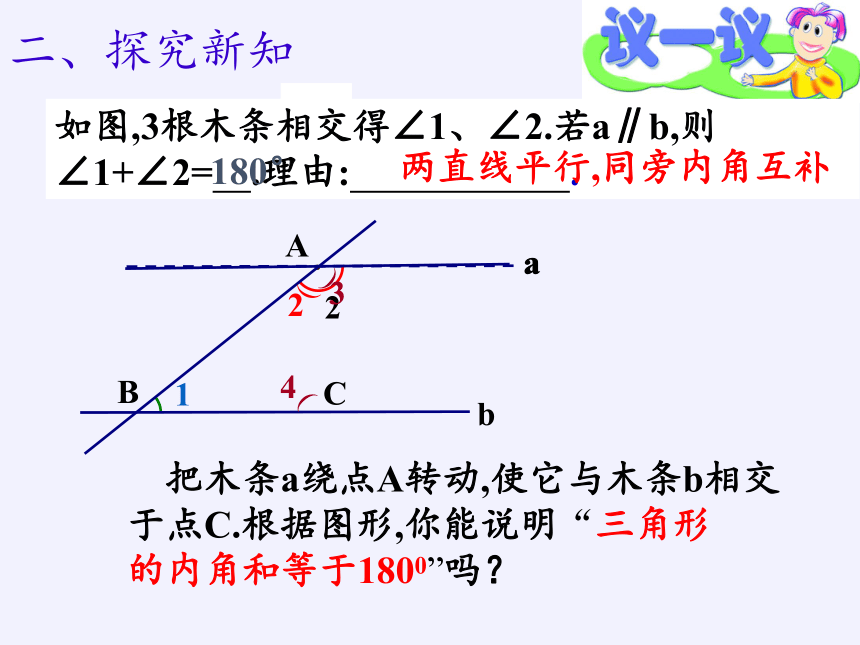
如图,3根木条相交得∠1、∠2.若a∥b,则∠1+∠2= .理由: .
两直线平行,同旁内角互补
180°
C
把木条a绕点A转动,使它与木条b相交于点C.根据图形,你能说明“三角形
的内角和等于1800”吗?
(
2
(
4
(
3
a
二、探究新知
思路总结
为了说明3个角的和为1800,可转化为一个平角或同旁内角互补,这种转化思想是数学中的常用思想方法.
三角形的内角和定理:
三角形的内角和为180度。
1、根据下图填空:
⌒
81°
⌒
72°
⌒
n°
(1)
⌒
x°
⌒
122°
⌒
x°
(2)
∟
⌒
31°
⌒
y°
(3)
(1)n=_____(2)x=_____(3)y=_____
27
29
59
小试牛刀
2.在△ABC中,若∠A=∠B=40°,
则△ABC是( ).
A.直角三角形 B.锐角三角形
C.钝角三角形 D.以上都不对
C
3、在一个三角形的3个内角中,
最多能有__个锐角;
3
1
1
最多能有__个直角;
最多能有 __个钝角。
例1:如图,在△ABC中,∠A=3∠C,∠B=2∠C,求三个内角的度数。
三、例题精讲
若将条件改为∠A:∠B:∠C=2:3:4,又如何解呢?
⌒
⌒
⌒
例2
已知如图,△ABC中∠ABC与
∠ACB的平分线相交于点D,
(1)若∠A=70°,求∠D的度数.
(2)若∠D =110 °,则∠A =___ °
我有哪些收获呢?
与大家共分享!
学 而 不 思 则 罔
回头一看,我想说…
1、△ABC中,若∠A+∠B=90°,
则△ABC是( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
检测一下你自己
2、在△ABC中,∠A∶∠B∶∠C=5∶6∶7,
则∠A=___°,∠B=___°,∠C=___°.
4、 如图,在△ABC中,CD平分∠ACB,
∠A=700,∠B=500,求∠BCD,∠BDC的度数。
A
B
C
D
E
3、如图,AC、BD相交于点O,∠A=32°,
∠B=50°,∠C=55°,则∠D=___°
B
A
O
C
D
思考题
如图:试求出图中∠1+∠2+∠3的度数.
⌒
⌒
⌒
谢 谢
7.5 多边形的内角和与外角和
2、能运用三角形内角和定理进行有关的说理与计算.
学习目标
1、探索三角形三个内角之间的关系.
内角三兄弟之争
在一个直角三角形里住着三个内角兄弟,
平时三兄弟非常团结。可是有一天,老二
突然不高兴,发起脾气来,它指着老大直角
说:“你凭什么度数最大,我也要和你一样大!”
老大说:“不行呀,这是不可能的,否则,
我们这个家就再也围不起来了…”
“为什么?”老二很纳闷。
同学们,你们知道其中的道理吗?
一、情境创设
想一想
三角形的3个内角和是1800
小学里我们用什么方法验证呢
方法一: 度量
请每位同学在试卷上任意画一个三角形,用量角器量出各内角的度数,并求它们的和.
方法二:拼图
将三角形纸片的3个内角撕开,然后拼在一起,观察它们的和是否为180
你还有其他方法进行验证吗
1
2
a
b
A
B
如图,3根木条相交得∠1、∠2.若a∥b,则∠1+∠2= .理由: .
两直线平行,同旁内角互补
180°
C
把木条a绕点A转动,使它与木条b相交于点C.根据图形,你能说明“三角形
的内角和等于1800”吗?
(
2
(
4
(
3
a
二、探究新知
思路总结
为了说明3个角的和为1800,可转化为一个平角或同旁内角互补,这种转化思想是数学中的常用思想方法.
三角形的内角和定理:
三角形的内角和为180度。
1、根据下图填空:
⌒
81°
⌒
72°
⌒
n°
(1)
⌒
x°
⌒
122°
⌒
x°
(2)
∟
⌒
31°
⌒
y°
(3)
(1)n=_____(2)x=_____(3)y=_____
27
29
59
小试牛刀
2.在△ABC中,若∠A=∠B=40°,
则△ABC是( ).
A.直角三角形 B.锐角三角形
C.钝角三角形 D.以上都不对
C
3、在一个三角形的3个内角中,
最多能有__个锐角;
3
1
1
最多能有__个直角;
最多能有 __个钝角。
例1:如图,在△ABC中,∠A=3∠C,∠B=2∠C,求三个内角的度数。
三、例题精讲
若将条件改为∠A:∠B:∠C=2:3:4,又如何解呢?
⌒
⌒
⌒
例2
已知如图,△ABC中∠ABC与
∠ACB的平分线相交于点D,
(1)若∠A=70°,求∠D的度数.
(2)若∠D =110 °,则∠A =___ °
我有哪些收获呢?
与大家共分享!
学 而 不 思 则 罔
回头一看,我想说…
1、△ABC中,若∠A+∠B=90°,
则△ABC是( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
检测一下你自己
2、在△ABC中,∠A∶∠B∶∠C=5∶6∶7,
则∠A=___°,∠B=___°,∠C=___°.
4、 如图,在△ABC中,CD平分∠ACB,
∠A=700,∠B=500,求∠BCD,∠BDC的度数。
A
B
C
D
E
3、如图,AC、BD相交于点O,∠A=32°,
∠B=50°,∠C=55°,则∠D=___°
B
A
O
C
D
思考题
如图:试求出图中∠1+∠2+∠3的度数.
⌒
⌒
⌒
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
