华东师大版八年级下册数学 18.1 平行四边形的性质 课件 (共22张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 18.1 平行四边形的性质 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 15:37:53 | ||
图片预览





文档简介
(共21张PPT)
18.1 平行四边形的性质
运用广泛
美观别致
定义
18.1.1平行四边形的性质1
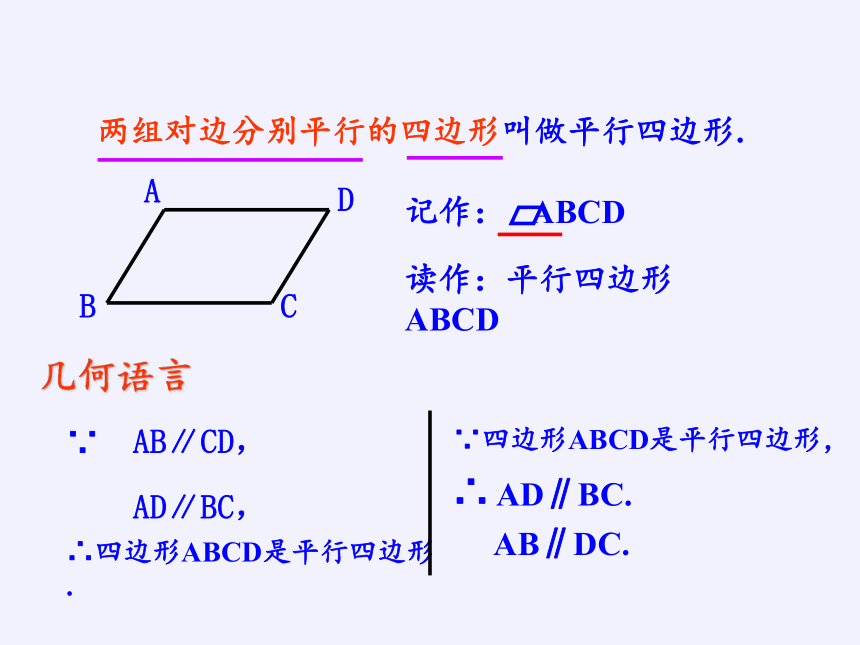
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
∴四边形ABCD是平行四边形.
∴ AD∥BC.
AB∥CD,
AD∥BC,
∵
AB∥DC.
∵四边形ABCD是平行四边形,
几何语言
平行四边形性质:
探究一:(1)根据定义画一个平行四边形;
自主研究
(3)度量一下,是不是和你的猜想一致?
(2)观察这个平行四边形,它的边、角之间有什么关系;
D
B
C
A
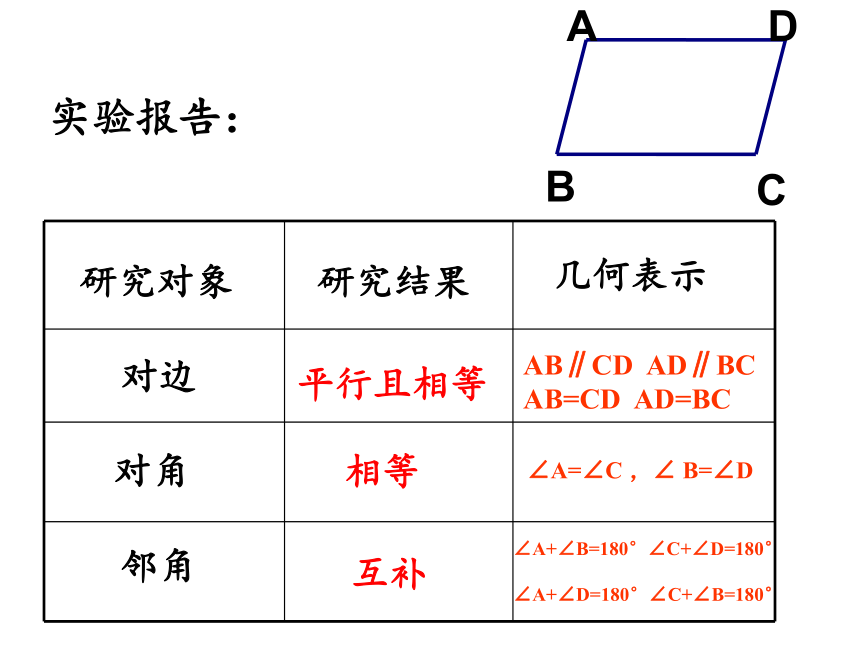
实验报告:
研究对象
研究结果
几何表示
对边
对角
邻角
平行且相等
AB∥CD AD∥BC
AB=CD AD=BC
相等
互补
∠A=∠C ,∠ B=∠D
∠A+∠B=180°∠C+∠D=180°
∠A+∠D=180°∠C+∠B=180°
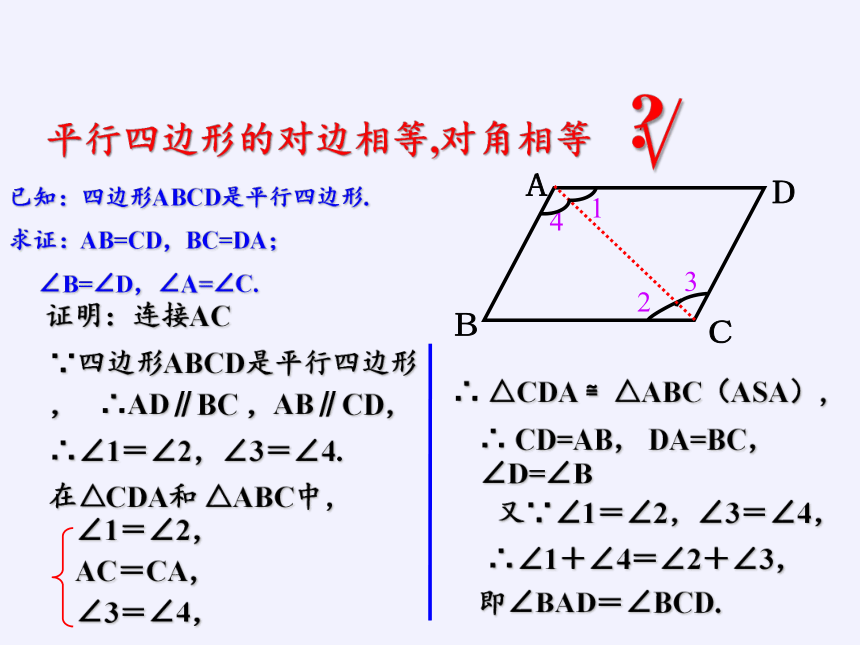
已知:四边形ABCD是平行四边形.
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
平行四边形的对边相等,对角相等
A
B
C
D
1
2
3
4
即∠BAD=∠BCD.
∵四边形ABCD是平行四边形, ∴AD∥BC ,AB∥CD,
∴∠1=∠2,∠3=∠4.
∠1=∠2,
AC=CA,
∠3=∠4,
∴ △CDA ≌△ABC(ASA),
∴ CD=AB, DA=BC, ∠D=∠B
在△CDA和 △ABC中,
证明:连接AC
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3,
√
1、已知平行四边形ABCD,BD为对角线(如图)∠A=70°, ∠BDC=30°。
求: ∠C = , ∠ADB = ,
∠ABD = ,
A
B
D
C
)
挑战第一关
2、在平行四边形ABCD中,
若AE平分∠DAB,AB=5cm,
AD=9cm,则EC= 。
探究二:将两个刚做好的完全一样的平行四边形中一个固定,另一个旋转1800,看看旋转后是否和固定的一个重合。
自主研究
平行四边形性质:
●
A
D
O
C
B
D
B
O
C
A
实验报告:
研究对象
研究结果
几何表示
对称性
对角线
中心对称图形
互相平分
OA=OC ,
O B=OD
在平行四边形ABCD中,对角线AC、BD交于点O,那么图中的全等三角形有 对。
挑战第二关
对边平行且相等
对角相等、邻角互补
对角线互相平分
边
角
对角线
对称性
中心对称
平行四边形问题
转化
两个全等三角形问题
通过这节课的学习
我收获了。。。
谢谢聆听!
在平行四边形ABCD中,周长为24cm,AD-AB=4cm且 ∠A:∠B=3:1 ,
1)求AB的长度
2)求∠C 的度数。
C
B
A
D
挑战第三关
挑战第三关
在□ABCD中, 点E、F分别为边BC、AD的中点,求证: △ABE ≌ △CDF
在平行四边形ABCD中,对角线AC、BD交于点O,AB ⊥ AC,AB= 1, BC=
1)求平行四边形ABCD的面积;
2)求对角线BD的长。
挑战第三关
视野拓展
挑战第四关
如图,四边形形ABCD是平行四边形,已知点P是CD上一点, 且AP和BP分别平分∠DAB和 ∠DAB。
(1)求∠A P B的度数;
(2)如果AP=8,AD=5,求三角形A P B的周长。
谢 谢
18.1 平行四边形的性质
运用广泛
美观别致
定义
18.1.1平行四边形的性质1
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
∴四边形ABCD是平行四边形.
∴ AD∥BC.
AB∥CD,
AD∥BC,
∵
AB∥DC.
∵四边形ABCD是平行四边形,
几何语言
平行四边形性质:
探究一:(1)根据定义画一个平行四边形;
自主研究
(3)度量一下,是不是和你的猜想一致?
(2)观察这个平行四边形,它的边、角之间有什么关系;
D
B
C
A
实验报告:
研究对象
研究结果
几何表示
对边
对角
邻角
平行且相等
AB∥CD AD∥BC
AB=CD AD=BC
相等
互补
∠A=∠C ,∠ B=∠D
∠A+∠B=180°∠C+∠D=180°
∠A+∠D=180°∠C+∠B=180°
已知:四边形ABCD是平行四边形.
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
平行四边形的对边相等,对角相等
A
B
C
D
1
2
3
4
即∠BAD=∠BCD.
∵四边形ABCD是平行四边形, ∴AD∥BC ,AB∥CD,
∴∠1=∠2,∠3=∠4.
∠1=∠2,
AC=CA,
∠3=∠4,
∴ △CDA ≌△ABC(ASA),
∴ CD=AB, DA=BC, ∠D=∠B
在△CDA和 △ABC中,
证明:连接AC
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3,
√
1、已知平行四边形ABCD,BD为对角线(如图)∠A=70°, ∠BDC=30°。
求: ∠C = , ∠ADB = ,
∠ABD = ,
A
B
D
C
)
挑战第一关
2、在平行四边形ABCD中,
若AE平分∠DAB,AB=5cm,
AD=9cm,则EC= 。
探究二:将两个刚做好的完全一样的平行四边形中一个固定,另一个旋转1800,看看旋转后是否和固定的一个重合。
自主研究
平行四边形性质:
●
A
D
O
C
B
D
B
O
C
A
实验报告:
研究对象
研究结果
几何表示
对称性
对角线
中心对称图形
互相平分
OA=OC ,
O B=OD
在平行四边形ABCD中,对角线AC、BD交于点O,那么图中的全等三角形有 对。
挑战第二关
对边平行且相等
对角相等、邻角互补
对角线互相平分
边
角
对角线
对称性
中心对称
平行四边形问题
转化
两个全等三角形问题
通过这节课的学习
我收获了。。。
谢谢聆听!
在平行四边形ABCD中,周长为24cm,AD-AB=4cm且 ∠A:∠B=3:1 ,
1)求AB的长度
2)求∠C 的度数。
C
B
A
D
挑战第三关
挑战第三关
在□ABCD中, 点E、F分别为边BC、AD的中点,求证: △ABE ≌ △CDF
在平行四边形ABCD中,对角线AC、BD交于点O,AB ⊥ AC,AB= 1, BC=
1)求平行四边形ABCD的面积;
2)求对角线BD的长。
挑战第三关
视野拓展
挑战第四关
如图,四边形形ABCD是平行四边形,已知点P是CD上一点, 且AP和BP分别平分∠DAB和 ∠DAB。
(1)求∠A P B的度数;
(2)如果AP=8,AD=5,求三角形A P B的周长。
谢 谢
