2021—2022学年苏科版数学八年级下册9.4.2菱形课后补充习题分层练(Word版含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级下册9.4.2菱形课后补充习题分层练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 441.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 15:04:40 | ||
图片预览



文档简介
9.4.2菱形-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)
【A夯实基础】
A1、(2020秋 滕州市月考)菱形具有而平行四边形不一定具有的性质是( )
A.对角线垂直 B.对边相等
C.对角相等 D.对角线互相平分
A2、(2020 宁波模拟)如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
A3、在菱形ABCD中,AC=12,BD=16,则该菱形的面积是( )
A.10 B.40 C.96 D.192
A4、(2020春 如皋市期末)如图,四边形ABCD是菱形,∠DAB=48°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO= 度.
A5、如图,平面直角坐标系中,菱形ABCD的顶点A(3,0),B(﹣2,0),顶点D在y轴正半轴上,
则点C的坐标为( )
A.(﹣3,4) B.(﹣4,5) C.(﹣5,5) D.(﹣5,4)
A6、(2021春 玄武区校级期中)如图所示,在菱形中,、相交于,,是线段上一点,则的度数可能是
A. B. C. D.
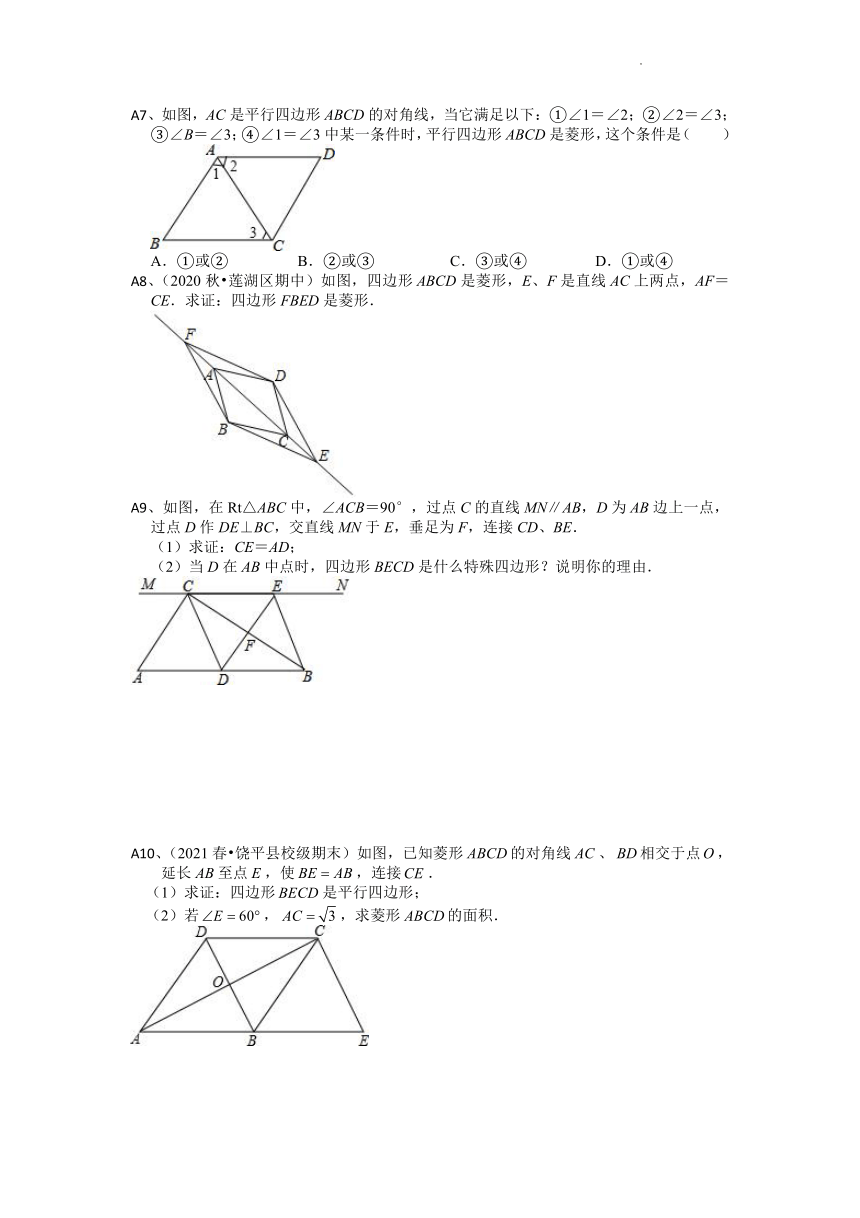
A7、如图,AC是平行四边形ABCD的对角线,当它满足以下:①∠1=∠2;②∠2=∠3;③∠B=∠3;④∠1=∠3中某一条件时,平行四边形ABCD是菱形,这个条件是( )
A.①或② B.②或③ C.③或④ D.①或④
A8、(2020秋 莲湖区期中)如图,四边形ABCD是菱形,E、F是直线AC上两点,AF=CE.求证:四边形FBED是菱形.
A9、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
A10、(2021春 饶平县校级期末)如图,已知菱形的对角线、相交于点,延长至点,使,连接.
(1)求证:四边形是平行四边形;
(2)若,,求菱形的面积.
【B培优综合】
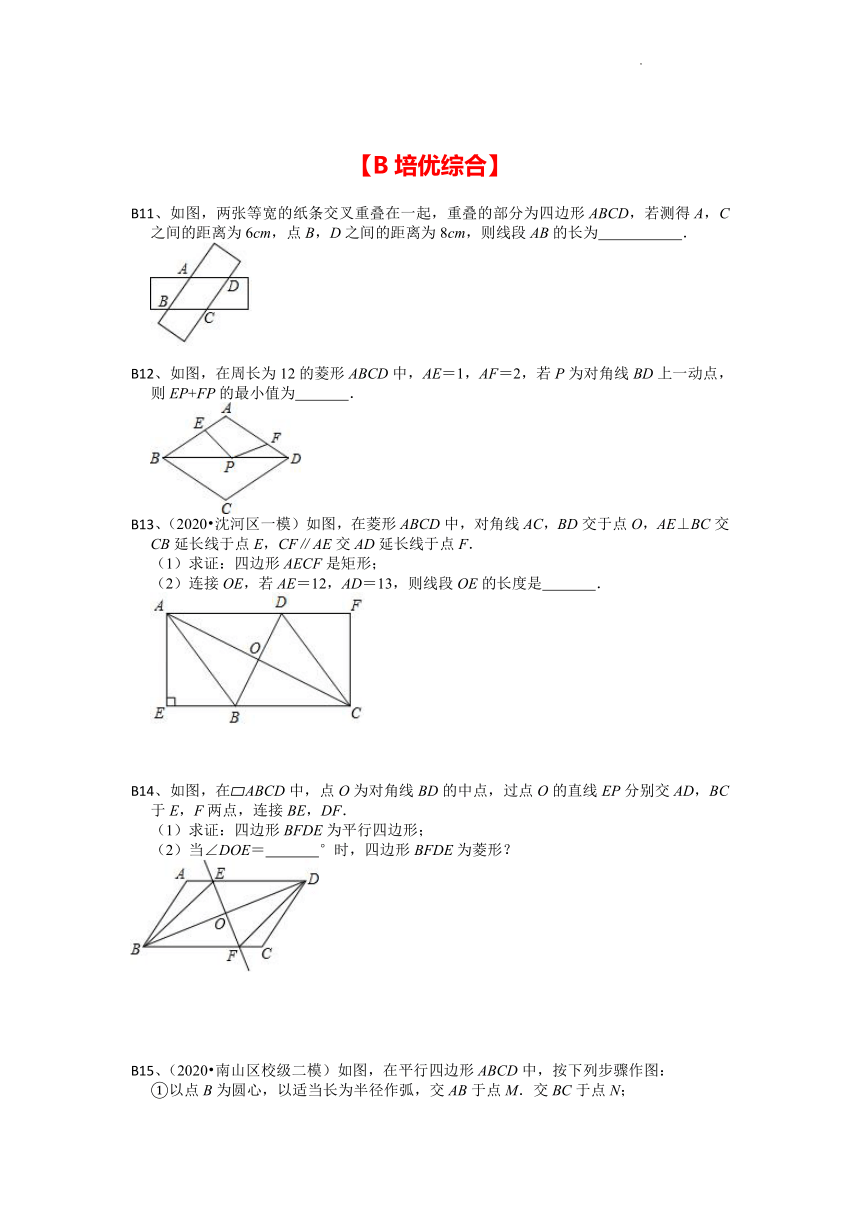
B11、如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为 .
B12、如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为 .
B13、(2020 沈河区一模)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于点E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=12,AD=13,则线段OE的长度是 .
B14、如图,在 ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.
(1)求证:四边形BFDE为平行四边形;
(2)当∠DOE= °时,四边形BFDE为菱形?
B15、(2020 南山区校级二模)如图,在平行四边形ABCD中,按下列步骤作图:
①以点B为圆心,以适当长为半径作弧,交AB于点M.交BC于点N;
②再分别以点M和点N为圆心,大于MN的长为半径作弧,两弧交于点G;
③作射线BG交AD于F;④过点A作AE⊥BF交BF于点P,交BC于点E;
⑤连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=8,AD=10,∠ABC=60°,求DP的长.
B16、如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=13,CF=6,求四边形BDFG的周长.
【C拔尖拓展】
C17、(2019春 江阴市期末)如图,是一张平行四边形纸片, 要求利用所学知识作出一个菱形, 甲、 乙两位同学的作法如下: 则关于甲、 乙两人的作法, 下列判断正确的为
A . 仅甲正确 B . 仅乙正确 C . 甲、 乙均正确 D . 甲、 乙均错误
C18、如图,在菱形ABCD中,AE⊥BC于点E
(1)若∠BAE=30°,AE=3,求菱形ABCD的周长.
(2)作AF⊥CD于点F,连结EF,BD,求证:EF∥BD.
(3)设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2,求S1﹣S2的值.
9.4.2菱形-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、(2020秋 滕州市月考)菱形具有而平行四边形不一定具有的性质是( )
A.对角线垂直 B.对边相等
C.对角相等 D.对角线互相平分
【思路点拨】利用菱形的性质和平行四边形的性质进行判断可求解.
【答案】解:∵菱形具有的性质有:四边相等,两组对边平行且相等,两组对角分别相等,对角线互相平分,对角线互相垂直;
平行四边形的性质有:两组对边分别平行且相等,两组对角分别相等,对角线互相平分,
∴菱形具有而平行四边形不一定具有的性质是四边相等,对角线互相垂直,
故选:A.
A2、(2020 宁波模拟)如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
【思路点拨】由已知条件得出四边形ABCD是平行四边形,再由一组邻边相等,即可得出四边形ABCD是菱形.
【答案】解:需要添加的条件是AB=BC;
理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形(一组邻边相等的平行四边形是菱形);
故选:D.
A3、在菱形ABCD中,AC=12,BD=16,则该菱形的面积是( )
A.10 B.40 C.96 D.192
解:∵四边形ABCD是菱形,AC=12,BD=16,
∴菱形ABCD的面积=AC×BD=×12×16=96;
故选:C.
A4、(2020春 如皋市期末)如图,四边形ABCD是菱形,∠DAB=48°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO= 度.
【分析】本题考查了菱形的性质,直角三角形斜边上的中线等于斜边的一半的性质,以及等角的余角相等,熟记各性质并理清图中角度的关系是解题的关键.
由菱形的性质可得OD=OB,∠COD=90°,由直角三角形的性质可得OH=BD=OB,可得∠OHB=∠OBH,由余角的性质可求解.
【答案】解:∵四边形ABCD是菱形,∴OD=OB,∠COD=90°,∠DAB=∠DCB=48°,
∵DH⊥AB,∴OH=BD=OB,∴∠OHB=∠OBH,
又∵AB∥CD,∴∠OBH=∠ODC,
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠DCO=∠DCB=24°,
故答案为:24.
A5、如图,平面直角坐标系中,菱形ABCD的顶点A(3,0),B(﹣2,0),顶点D在y轴正半轴上,
则点C的坐标为( )
A.(﹣3,4) B.(﹣4,5) C.(﹣5,5) D.(﹣5,4)
解:∵菱形ABCD的顶点A(3,0),B(﹣2,0),∴CD=AD=AB=5,OA=3,
∴OD===4
∵AB∥CD,∴点C的坐标为(﹣5,4) 故选:D.
A6、(2021春 玄武区校级期中)如图所示,在菱形中,、相交于,,是线段上一点,则的度数可能是
A. B. C. D.
【分析】由菱形的性质可得,,可得,由三角形的外角性质可求解.
【解析】四边形是菱形,,
,,
,
,
,
故选:.
A7、如图,AC是平行四边形ABCD的对角线,当它满足以下:①∠1=∠2;②∠2=∠3;③∠B=∠3;④∠1=∠3中某一条件时,平行四边形ABCD是菱形,这个条件是( )
A.①或② B.②或③ C.③或④ D.①或④
【思路点拨】由四边形ABCD是平行四边形,易得∠2=∠3,又由∠1=∠2,可得∠1=∠3,即可证得AB=BC,继而判定平行四边形ABCD是菱形.
【答案】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠2=∠3,
∵∠1=∠2,∴∠1=∠3,∴AB=BC,
∴平行四边形ABCD是菱形;故①④能判定.
故选:D.
A8、(2020秋 莲湖区期中)如图,四边形ABCD是菱形,E、F是直线AC上两点,AF=CE.求证:四边形FBED是菱形.
【思路点拨】连接BD交AC于O,根据菱形的判定和性质定理即可得到结论.
【答案】证明:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∵AF=CE,
∴OF=OE,
∴四边形FBED是菱形.
A9、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
解答:(1)证明:∵DE⊥BC,∴∠DFB=90°,
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,
∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,∴AD=BD,
∵CE=AD,∴BD=CE,
∵BD∥CE,∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,∴CD=BD,∴四边形BECD是菱形.
A10、(2021春 饶平县校级期末)如图,已知菱形的对角线、相交于点,延长至点,使,连接.
(1)求证:四边形是平行四边形;
(2)若,,求菱形的面积.
【分析】(1)根据菱形的对边平行且相等可得,,然后证明得到,,从而证明四边形是平行四边形;
(2)欲求菱形的面积,已知,只需求得的长度即可(利用平行四边形以及菱形的性质可得,再利用勾股定理可求出的长度).最后利用菱形的面积等于两对角线乘积的一半即可求解.
【解析】(1)证明:四边形是菱形,,,
又,,,四边形是平行四边形;
(2)四边形是平行四边形,,
四边形是菱形,,,,
中,,,,
设,,
由题意得,解得(负值舍去),,
四边形是平行四边形,,
菱形的面积.
【B培优综合】
B11、如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为 .
【解析】解:如图,作AR⊥BC于R,AS⊥CD于S,连接AC,BD交于点O,
由题意知,AD∥BC,AB∥CD,∴四边形ABCD是平行四边形.
∵两张纸条等宽,∴AR=AS.
∵AR BC=AS CD,∴BC=CD,∴平行四边形ABCD是菱形,∴AC⊥BD.
在Rt△AOB中,OA=3cm,OB=4cm,∴AB==5(cm).
故答案是:5cm.
B12、如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为 .
【分析】作F点关于BD的对称点F′,则PF=PF′,由两点之间线段最短可知当E、P、F′在一条直线上时,EP+FP有最小值,然后求得EF′的长度即可.
【答案】解:作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,
此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,∴DF=AE=1,∴四边形AEF′D是平行四边形,
∴EF′=AD=3.∴EP+FP的最小值为3.
故答案为:3.
B13、(2020 沈河区一模)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于点E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=12,AD=13,则线段OE的长度是 .
【思路点拨】本题考查了矩形的判定和性质,菱形的性质,解直角三角形,正确的识别图形是解题的关键.
(1)根据菱形的性质得到AD∥BC,推出四边形AECF是平行四边形,根据矩形的判定定理即可得到结论;
(2)根据已知条件得到得到CE=18.根据勾股定理得到AC=6,于是得到结论.
【答案】(1)证明:∵四边形ABCD是菱形,∴AD∥BC,
∵CF∥AE,∴四边形AECF是平行四边形.
∵AE⊥BC,∴∠AEC=90°,∴平行四边形AECF是矩形;
(2)解:∵AE=12,AD=13,∴AB=13,∴BE=5,
∵AB=BC=13,∴CE=18,
∴AC===6,
∵对角线AC,BD交于点O,∴AO=CO=3.∴OE=3,
故答案为:3.
B14、如图,在 ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.
(1)求证:四边形BFDE为平行四边形;
(2)当∠DOE= °时,四边形BFDE为菱形?
解答:(1)证明:∵四边形ABCD是平行四边形,O为对角线BD的中点,
∴BO=DO,AD∥BC, ∴∠EDB=∠FBO,
在△EOD和△FOB中,, ∴△DOE≌△BOF(ASA),∴DE=BF,
又∵DE∥BF,∴四边形BFDE为平行四边形;
(2)解:∠DOE=90°时,四边形BFDE为菱形;理由如下:
由(1)得:四边形BFDE是平行四边形,
若∠DOE=90°,则EF⊥BD,∴四边形BFDE为菱形; 故答案为:90.
B15、(2020 南山区校级二模)如图,在平行四边形ABCD中,按下列步骤作图:
①以点B为圆心,以适当长为半径作弧,交AB于点M.交BC于点N;
②再分别以点M和点N为圆心,大于MN的长为半径作弧,两弧交于点G;
③作射线BG交AD于F;④过点A作AE⊥BF交BF于点P,交BC于点E;
⑤连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=8,AD=10,∠ABC=60°,求DP的长.
【思路点拨】本题考查了菱形的判定及平行四边形的性质,解题的关键是牢记菱形的几个判定定理,难度不大.
(1)根据线段垂直平分线的性质和平行四边形的性质即可得到结论;
(2)作PH⊥AD于H,根据四边形ABEF是菱形,∠ABC=60°,AB=8,得到AB=AF=8,∠ABF=∠ADB=30°,AP⊥BF,从而得到PH=2,DH=10,然后利用锐角三角函数的定义求解即可.
【答案】(1)证明:由作图知BA=BE,∠ABF=∠EBF,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠EBF=∠AFB,∴∠ABF=∠AFB,
∴AB=AF=BE,∴四边形ABEF是平行四边形,
又AB=BE,∴四边形ABEF是菱形;
(2)解:作PH⊥AD于H,
∵四边形ABEF是菱形,∠ABC=60°,AB=8,
∴AB=AF=8,∠ABF=∠AFB=30°,AP⊥BF,
∴AP=AB=4,∴PH=2,DH=8,
∴DP===2.
B16、如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=13,CF=6,求四边形BDFG的周长.
(1)证明:∵∠ABC=90°,BD为AC的中线,∴BD=AC,
∵AG∥BD,BD=FG,∴四边形BGFD是平行四边形,
∵CF⊥BD,∴CF⊥AG,
又∵点D是AC中点,∴DF=AC,∴BD=DF;
(2)证明:∵BD=DF,∴四边形BGFD是菱形,
(3)解:设GF=x,则AF=13﹣x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,解得:x=5,
∴四边形BDFG的周长=4GF=20.
【C拔尖拓展】
C17、(2019春 江阴市期末)如图,是一张平行四边形纸片, 要求利用所学知识作出一个菱形, 甲、 乙两位同学的作法如下: 则关于甲、 乙两人的作法, 下列判断正确的为
A . 仅甲正确 B . 仅乙正确 C . 甲、 乙均正确 D . 甲、 乙均错误
【分析】首先证明,可得,再根据一组对边平行且相等的四边形是平行四边形可判定判定四边形是平行四边形, 再由,可根据对角线互相垂直的四边形是菱形判定出是菱形;四边形是平行四边形, 可根据角平分线的定义和平行线的定义, 求得,所以四边形是菱形 .
【解析】 甲的作法正确;
四边形是平行四边形,,,
是的垂直平分线,,
在和中,,,,
又,四边形是平行四边形,
,四边形是菱形;
乙的作法正确;
,,,
平分,平分,,,
,,,,
,且,四边形是平行四边形,
,平行四边形是菱形;
故选:.
C18、如图,在菱形ABCD中,AE⊥BC于点E
(1)若∠BAE=30°,AE=3,求菱形ABCD的周长.
(2)作AF⊥CD于点F,连结EF,BD,求证:EF∥BD.
(3)设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2,求S1﹣S2的值.
【思路点拨】本题考查了菱形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、平行线的判定、勾股定理、三角形面积等知识;熟练掌握菱形的性质,证明三角形全等是解题的关键.
(1)由直角三角形的性质和勾股定理得出BE=AB,BE2+AE2=AB2,求出AB=2,即可得出结果;
(2)证明△ABE≌△ADF,得出BE=DF,证出CE=CF,由等腰三角形的性质得出∠CEF=∠CBD=(180°﹣∠C),即可得出结论;
(3)连接CG,证明△ADG≌△CDG,得出AG=CG,△ADG和△CDG的面积相等,得出S1﹣S2=S△CGE,AB=BC=CE+BE=12,由勾股定理得出AE==4,设EG=x,则AG=CG=4﹣x,由勾股定理得出方程,求出EG=,即可得出结果.
【答案】(1)解:∵AE⊥BC,∠BAE=30°,∴BE=AB,BE2+AE2=AB2,
∵AE=3,∴(AB)2+32=AB2,解得:AB=2,
∴菱形ABCD的周长=2×4=8;
(2)证明:∵四边形ABCD是菱形,∴∠ABE=∠ADF,AB=AD=BC=CD,
∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°,
在△ABE和△ADF中,,
∴△ABE≌△ADF(AAS),∴BE=DF,
∵BC=CD,∴CE=CF,∴∠CEF=∠CBD=(180°﹣∠C),∴EF∥BD;
(3)解:连接CG,如图所示:
∵四边形ABCD是菱形,∴∠ADG=∠CDG,AD=CD,
在△ADG和△CDG中,,∴△ADG≌△CDG(SAS),
∴AG=CG,△ADG和△CDG的面积相等,∴S1﹣S2=S△CGE,
AB=BC=CE+BE=4+8=12,
∵AE⊥BC,∴AE===4,
设EG=x,则AG=CG=4﹣x,
∵AE⊥BC,∴EG2+EC2=CG2,即:x2+42=(4﹣x)2,
解得:x=,即EG=,
∴S1﹣S2=S△CGE=CE EG=×4×=.
-2021-2022学年八年级数学下册 (苏科版)
【A夯实基础】
A1、(2020秋 滕州市月考)菱形具有而平行四边形不一定具有的性质是( )
A.对角线垂直 B.对边相等
C.对角相等 D.对角线互相平分
A2、(2020 宁波模拟)如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
A3、在菱形ABCD中,AC=12,BD=16,则该菱形的面积是( )
A.10 B.40 C.96 D.192
A4、(2020春 如皋市期末)如图,四边形ABCD是菱形,∠DAB=48°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO= 度.
A5、如图,平面直角坐标系中,菱形ABCD的顶点A(3,0),B(﹣2,0),顶点D在y轴正半轴上,
则点C的坐标为( )
A.(﹣3,4) B.(﹣4,5) C.(﹣5,5) D.(﹣5,4)
A6、(2021春 玄武区校级期中)如图所示,在菱形中,、相交于,,是线段上一点,则的度数可能是
A. B. C. D.
A7、如图,AC是平行四边形ABCD的对角线,当它满足以下:①∠1=∠2;②∠2=∠3;③∠B=∠3;④∠1=∠3中某一条件时,平行四边形ABCD是菱形,这个条件是( )
A.①或② B.②或③ C.③或④ D.①或④
A8、(2020秋 莲湖区期中)如图,四边形ABCD是菱形,E、F是直线AC上两点,AF=CE.求证:四边形FBED是菱形.
A9、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
A10、(2021春 饶平县校级期末)如图,已知菱形的对角线、相交于点,延长至点,使,连接.
(1)求证:四边形是平行四边形;
(2)若,,求菱形的面积.
【B培优综合】
B11、如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为 .
B12、如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为 .
B13、(2020 沈河区一模)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于点E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=12,AD=13,则线段OE的长度是 .
B14、如图,在 ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.
(1)求证:四边形BFDE为平行四边形;
(2)当∠DOE= °时,四边形BFDE为菱形?
B15、(2020 南山区校级二模)如图,在平行四边形ABCD中,按下列步骤作图:
①以点B为圆心,以适当长为半径作弧,交AB于点M.交BC于点N;
②再分别以点M和点N为圆心,大于MN的长为半径作弧,两弧交于点G;
③作射线BG交AD于F;④过点A作AE⊥BF交BF于点P,交BC于点E;
⑤连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=8,AD=10,∠ABC=60°,求DP的长.
B16、如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=13,CF=6,求四边形BDFG的周长.
【C拔尖拓展】
C17、(2019春 江阴市期末)如图,是一张平行四边形纸片, 要求利用所学知识作出一个菱形, 甲、 乙两位同学的作法如下: 则关于甲、 乙两人的作法, 下列判断正确的为
A . 仅甲正确 B . 仅乙正确 C . 甲、 乙均正确 D . 甲、 乙均错误
C18、如图,在菱形ABCD中,AE⊥BC于点E
(1)若∠BAE=30°,AE=3,求菱形ABCD的周长.
(2)作AF⊥CD于点F,连结EF,BD,求证:EF∥BD.
(3)设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2,求S1﹣S2的值.
9.4.2菱形-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、(2020秋 滕州市月考)菱形具有而平行四边形不一定具有的性质是( )
A.对角线垂直 B.对边相等
C.对角相等 D.对角线互相平分
【思路点拨】利用菱形的性质和平行四边形的性质进行判断可求解.
【答案】解:∵菱形具有的性质有:四边相等,两组对边平行且相等,两组对角分别相等,对角线互相平分,对角线互相垂直;
平行四边形的性质有:两组对边分别平行且相等,两组对角分别相等,对角线互相平分,
∴菱形具有而平行四边形不一定具有的性质是四边相等,对角线互相垂直,
故选:A.
A2、(2020 宁波模拟)如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
【思路点拨】由已知条件得出四边形ABCD是平行四边形,再由一组邻边相等,即可得出四边形ABCD是菱形.
【答案】解:需要添加的条件是AB=BC;
理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形(一组邻边相等的平行四边形是菱形);
故选:D.
A3、在菱形ABCD中,AC=12,BD=16,则该菱形的面积是( )
A.10 B.40 C.96 D.192
解:∵四边形ABCD是菱形,AC=12,BD=16,
∴菱形ABCD的面积=AC×BD=×12×16=96;
故选:C.
A4、(2020春 如皋市期末)如图,四边形ABCD是菱形,∠DAB=48°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO= 度.
【分析】本题考查了菱形的性质,直角三角形斜边上的中线等于斜边的一半的性质,以及等角的余角相等,熟记各性质并理清图中角度的关系是解题的关键.
由菱形的性质可得OD=OB,∠COD=90°,由直角三角形的性质可得OH=BD=OB,可得∠OHB=∠OBH,由余角的性质可求解.
【答案】解:∵四边形ABCD是菱形,∴OD=OB,∠COD=90°,∠DAB=∠DCB=48°,
∵DH⊥AB,∴OH=BD=OB,∴∠OHB=∠OBH,
又∵AB∥CD,∴∠OBH=∠ODC,
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠DCO=∠DCB=24°,
故答案为:24.
A5、如图,平面直角坐标系中,菱形ABCD的顶点A(3,0),B(﹣2,0),顶点D在y轴正半轴上,
则点C的坐标为( )
A.(﹣3,4) B.(﹣4,5) C.(﹣5,5) D.(﹣5,4)
解:∵菱形ABCD的顶点A(3,0),B(﹣2,0),∴CD=AD=AB=5,OA=3,
∴OD===4
∵AB∥CD,∴点C的坐标为(﹣5,4) 故选:D.
A6、(2021春 玄武区校级期中)如图所示,在菱形中,、相交于,,是线段上一点,则的度数可能是
A. B. C. D.
【分析】由菱形的性质可得,,可得,由三角形的外角性质可求解.
【解析】四边形是菱形,,
,,
,
,
,
故选:.
A7、如图,AC是平行四边形ABCD的对角线,当它满足以下:①∠1=∠2;②∠2=∠3;③∠B=∠3;④∠1=∠3中某一条件时,平行四边形ABCD是菱形,这个条件是( )
A.①或② B.②或③ C.③或④ D.①或④
【思路点拨】由四边形ABCD是平行四边形,易得∠2=∠3,又由∠1=∠2,可得∠1=∠3,即可证得AB=BC,继而判定平行四边形ABCD是菱形.
【答案】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠2=∠3,
∵∠1=∠2,∴∠1=∠3,∴AB=BC,
∴平行四边形ABCD是菱形;故①④能判定.
故选:D.
A8、(2020秋 莲湖区期中)如图,四边形ABCD是菱形,E、F是直线AC上两点,AF=CE.求证:四边形FBED是菱形.
【思路点拨】连接BD交AC于O,根据菱形的判定和性质定理即可得到结论.
【答案】证明:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∵AF=CE,
∴OF=OE,
∴四边形FBED是菱形.
A9、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
解答:(1)证明:∵DE⊥BC,∴∠DFB=90°,
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,
∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,∴AD=BD,
∵CE=AD,∴BD=CE,
∵BD∥CE,∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,∴CD=BD,∴四边形BECD是菱形.
A10、(2021春 饶平县校级期末)如图,已知菱形的对角线、相交于点,延长至点,使,连接.
(1)求证:四边形是平行四边形;
(2)若,,求菱形的面积.
【分析】(1)根据菱形的对边平行且相等可得,,然后证明得到,,从而证明四边形是平行四边形;
(2)欲求菱形的面积,已知,只需求得的长度即可(利用平行四边形以及菱形的性质可得,再利用勾股定理可求出的长度).最后利用菱形的面积等于两对角线乘积的一半即可求解.
【解析】(1)证明:四边形是菱形,,,
又,,,四边形是平行四边形;
(2)四边形是平行四边形,,
四边形是菱形,,,,
中,,,,
设,,
由题意得,解得(负值舍去),,
四边形是平行四边形,,
菱形的面积.
【B培优综合】
B11、如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为 .
【解析】解:如图,作AR⊥BC于R,AS⊥CD于S,连接AC,BD交于点O,
由题意知,AD∥BC,AB∥CD,∴四边形ABCD是平行四边形.
∵两张纸条等宽,∴AR=AS.
∵AR BC=AS CD,∴BC=CD,∴平行四边形ABCD是菱形,∴AC⊥BD.
在Rt△AOB中,OA=3cm,OB=4cm,∴AB==5(cm).
故答案是:5cm.
B12、如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为 .
【分析】作F点关于BD的对称点F′,则PF=PF′,由两点之间线段最短可知当E、P、F′在一条直线上时,EP+FP有最小值,然后求得EF′的长度即可.
【答案】解:作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,
此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,∴DF=AE=1,∴四边形AEF′D是平行四边形,
∴EF′=AD=3.∴EP+FP的最小值为3.
故答案为:3.
B13、(2020 沈河区一模)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于点E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=12,AD=13,则线段OE的长度是 .
【思路点拨】本题考查了矩形的判定和性质,菱形的性质,解直角三角形,正确的识别图形是解题的关键.
(1)根据菱形的性质得到AD∥BC,推出四边形AECF是平行四边形,根据矩形的判定定理即可得到结论;
(2)根据已知条件得到得到CE=18.根据勾股定理得到AC=6,于是得到结论.
【答案】(1)证明:∵四边形ABCD是菱形,∴AD∥BC,
∵CF∥AE,∴四边形AECF是平行四边形.
∵AE⊥BC,∴∠AEC=90°,∴平行四边形AECF是矩形;
(2)解:∵AE=12,AD=13,∴AB=13,∴BE=5,
∵AB=BC=13,∴CE=18,
∴AC===6,
∵对角线AC,BD交于点O,∴AO=CO=3.∴OE=3,
故答案为:3.
B14、如图,在 ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.
(1)求证:四边形BFDE为平行四边形;
(2)当∠DOE= °时,四边形BFDE为菱形?
解答:(1)证明:∵四边形ABCD是平行四边形,O为对角线BD的中点,
∴BO=DO,AD∥BC, ∴∠EDB=∠FBO,
在△EOD和△FOB中,, ∴△DOE≌△BOF(ASA),∴DE=BF,
又∵DE∥BF,∴四边形BFDE为平行四边形;
(2)解:∠DOE=90°时,四边形BFDE为菱形;理由如下:
由(1)得:四边形BFDE是平行四边形,
若∠DOE=90°,则EF⊥BD,∴四边形BFDE为菱形; 故答案为:90.
B15、(2020 南山区校级二模)如图,在平行四边形ABCD中,按下列步骤作图:
①以点B为圆心,以适当长为半径作弧,交AB于点M.交BC于点N;
②再分别以点M和点N为圆心,大于MN的长为半径作弧,两弧交于点G;
③作射线BG交AD于F;④过点A作AE⊥BF交BF于点P,交BC于点E;
⑤连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=8,AD=10,∠ABC=60°,求DP的长.
【思路点拨】本题考查了菱形的判定及平行四边形的性质,解题的关键是牢记菱形的几个判定定理,难度不大.
(1)根据线段垂直平分线的性质和平行四边形的性质即可得到结论;
(2)作PH⊥AD于H,根据四边形ABEF是菱形,∠ABC=60°,AB=8,得到AB=AF=8,∠ABF=∠ADB=30°,AP⊥BF,从而得到PH=2,DH=10,然后利用锐角三角函数的定义求解即可.
【答案】(1)证明:由作图知BA=BE,∠ABF=∠EBF,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠EBF=∠AFB,∴∠ABF=∠AFB,
∴AB=AF=BE,∴四边形ABEF是平行四边形,
又AB=BE,∴四边形ABEF是菱形;
(2)解:作PH⊥AD于H,
∵四边形ABEF是菱形,∠ABC=60°,AB=8,
∴AB=AF=8,∠ABF=∠AFB=30°,AP⊥BF,
∴AP=AB=4,∴PH=2,DH=8,
∴DP===2.
B16、如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=13,CF=6,求四边形BDFG的周长.
(1)证明:∵∠ABC=90°,BD为AC的中线,∴BD=AC,
∵AG∥BD,BD=FG,∴四边形BGFD是平行四边形,
∵CF⊥BD,∴CF⊥AG,
又∵点D是AC中点,∴DF=AC,∴BD=DF;
(2)证明:∵BD=DF,∴四边形BGFD是菱形,
(3)解:设GF=x,则AF=13﹣x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,解得:x=5,
∴四边形BDFG的周长=4GF=20.
【C拔尖拓展】
C17、(2019春 江阴市期末)如图,是一张平行四边形纸片, 要求利用所学知识作出一个菱形, 甲、 乙两位同学的作法如下: 则关于甲、 乙两人的作法, 下列判断正确的为
A . 仅甲正确 B . 仅乙正确 C . 甲、 乙均正确 D . 甲、 乙均错误
【分析】首先证明,可得,再根据一组对边平行且相等的四边形是平行四边形可判定判定四边形是平行四边形, 再由,可根据对角线互相垂直的四边形是菱形判定出是菱形;四边形是平行四边形, 可根据角平分线的定义和平行线的定义, 求得,所以四边形是菱形 .
【解析】 甲的作法正确;
四边形是平行四边形,,,
是的垂直平分线,,
在和中,,,,
又,四边形是平行四边形,
,四边形是菱形;
乙的作法正确;
,,,
平分,平分,,,
,,,,
,且,四边形是平行四边形,
,平行四边形是菱形;
故选:.
C18、如图,在菱形ABCD中,AE⊥BC于点E
(1)若∠BAE=30°,AE=3,求菱形ABCD的周长.
(2)作AF⊥CD于点F,连结EF,BD,求证:EF∥BD.
(3)设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2,求S1﹣S2的值.
【思路点拨】本题考查了菱形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、平行线的判定、勾股定理、三角形面积等知识;熟练掌握菱形的性质,证明三角形全等是解题的关键.
(1)由直角三角形的性质和勾股定理得出BE=AB,BE2+AE2=AB2,求出AB=2,即可得出结果;
(2)证明△ABE≌△ADF,得出BE=DF,证出CE=CF,由等腰三角形的性质得出∠CEF=∠CBD=(180°﹣∠C),即可得出结论;
(3)连接CG,证明△ADG≌△CDG,得出AG=CG,△ADG和△CDG的面积相等,得出S1﹣S2=S△CGE,AB=BC=CE+BE=12,由勾股定理得出AE==4,设EG=x,则AG=CG=4﹣x,由勾股定理得出方程,求出EG=,即可得出结果.
【答案】(1)解:∵AE⊥BC,∠BAE=30°,∴BE=AB,BE2+AE2=AB2,
∵AE=3,∴(AB)2+32=AB2,解得:AB=2,
∴菱形ABCD的周长=2×4=8;
(2)证明:∵四边形ABCD是菱形,∴∠ABE=∠ADF,AB=AD=BC=CD,
∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°,
在△ABE和△ADF中,,
∴△ABE≌△ADF(AAS),∴BE=DF,
∵BC=CD,∴CE=CF,∴∠CEF=∠CBD=(180°﹣∠C),∴EF∥BD;
(3)解:连接CG,如图所示:
∵四边形ABCD是菱形,∴∠ADG=∠CDG,AD=CD,
在△ADG和△CDG中,,∴△ADG≌△CDG(SAS),
∴AG=CG,△ADG和△CDG的面积相等,∴S1﹣S2=S△CGE,
AB=BC=CE+BE=4+8=12,
∵AE⊥BC,∴AE===4,
设EG=x,则AG=CG=4﹣x,
∵AE⊥BC,∴EG2+EC2=CG2,即:x2+42=(4﹣x)2,
解得:x=,即EG=,
∴S1﹣S2=S△CGE=CE EG=×4×=.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
