2021—2022学年苏科版数学八年级下册9.4.3正方形课后补充习题分层练(Word版含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级下册9.4.3正方形课后补充习题分层练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 290.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 14:52:10 | ||
图片预览

文档简介
9.4.3正方形-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)
【A夯实基础】
A1、已知正方形ABCD对角线AC,BD相交于点O,且AC=16cm,
则DO=_______cm,BO=______cm,∠OCD=_______度.
A2、(2020春 阿城区期末)正方形具有而菱形不具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线平分一组对角 D.对角线互相垂直
A3、(2020春 江阴市校级月考)如图,四边形ABCD中,AC、BD交于点O,则根据下列条件能判定它是正方形的是( )
A.∠DAB=90°且AD=BC B.AB=BC且AC=BD
C.∠DAB=90°且AC⊥BD D.AC⊥BD且AO=BO=CO=DO
A4、四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
A5、如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则∠CDE的度数为( )
A.20° B.22.5° C.25° D.30°
A6、如图,把含30°的直角三角板PMN放置在正方形ABCD中,,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则的度数为( )
A.60° B.65° C.75° D.80°
A7、如图,正方形ABCD中,点E、F分别在BC、CD上,且△AEF是等边三角形.求证:CE=CF.
A8、如图,AC为正方形ABCD的对角线,E为AC上一点,且AE=AB,过E作EF⊥AC,交BC于点F.
求证:BF=EF.
A9、如图,在正方形中,点E在边的延长线上,点F在边的延长线上,且连接 和相交于点M.求证:.
A10、已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F
(1)求证:△AEF≌△DEB;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【B培优综合】
B11、(2020春 西湖区校级月考)如图,正方形ABCD的边长为4,点E,F在对角线BD上,四边形AECF是菱形,且∠DAE=67.5°,则BE的长为( )
A. B.2 C.4﹣4 D.6﹣4
B12、如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O做ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.
B13、如图,在正方形ABCD中,E为CD上的一点,连接BE,若∠EBC=20°,将△EBC绕点C按顺时针方向旋转90°得到△FDC,连接EF,则∠EFD的度数为( )
A.15° B.20° C.25° D.30°
B14、已知平行四边形ABCD,对角线AC、BD相交于点O,且CA=CB,延长BC至点E,使CE=BC,连接DE.
(1)当AC⊥BD时,求证:BE=2CD;
(2)当∠ACB=90°时,求证:四边形ACED是正方形.
B15、(2020春 常州期末)如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
B16、(2020春 拱墅区期末)如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
【C拔尖拓展】
C17、如图,以边长为4的正方形ABCD的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于E、F两点,则线段EF的最小值为( )
A.2 B.4 C. D.2
C18、(1)尝试探究:
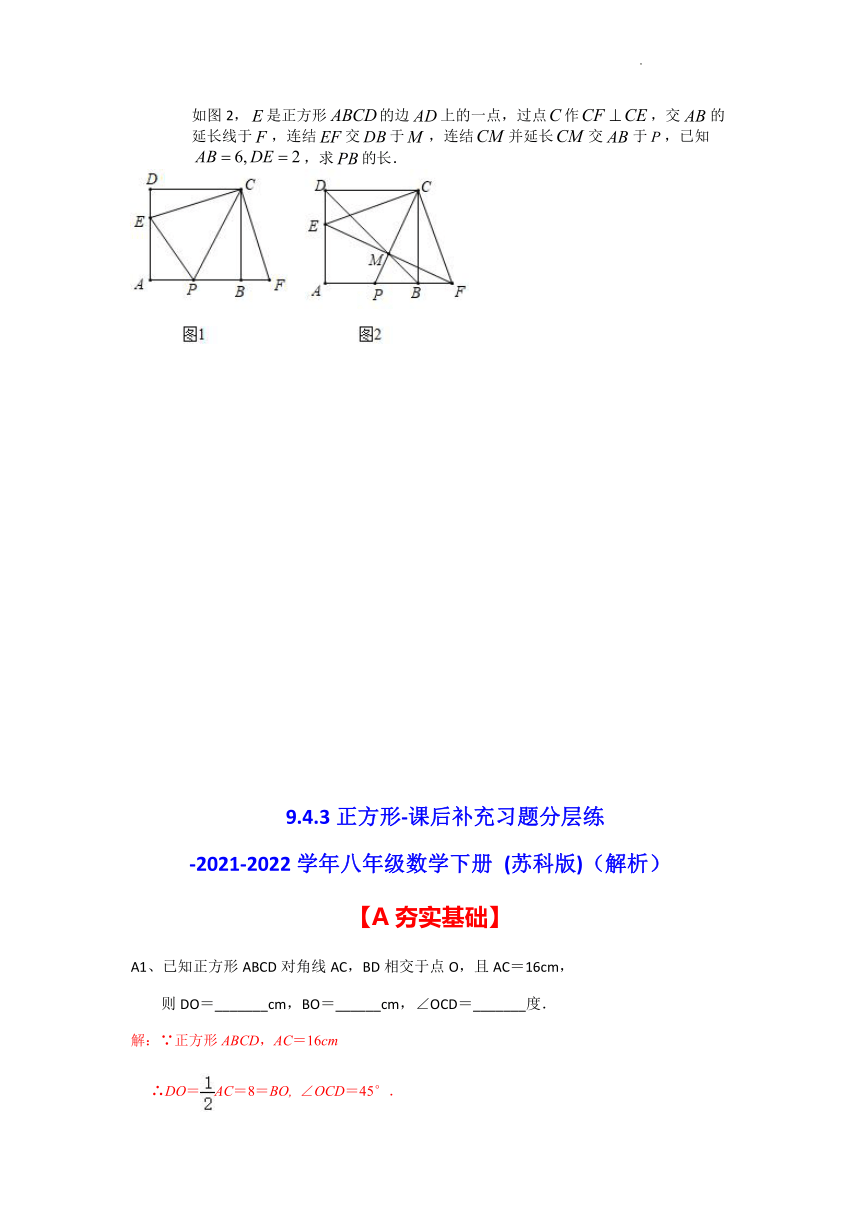
如图1,是正方形的边上的一点,过点作,交的延长线于.
①求证:;
②过点作的平分线交于,连结,请探究与的数量关系,
并证明你的结论.
(2)拓展应用:
如图2,是正方形的边上的一点,过点作,交的延长线于,连结交于,连结并延长交于,已知,求的长.
9.4.3正方形-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、已知正方形ABCD对角线AC,BD相交于点O,且AC=16cm,
则DO=_______cm,BO=______cm,∠OCD=_______度.
解:∵正方形ABCD,AC=16cm
∴DO=AC=8=BO, ∠OCD=45°.
故答案为8,8,45.
A2、(2020春 阿城区期末)正方形具有而菱形不具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线平分一组对角 D.对角线互相垂直
【思路点拨】根据正方形的性质以及菱形的性质即可判断.
【答案】解:正方形和菱形都满足:四条边都相等,对角线平分一组对角,对角线垂直且互相平分;
菱形的对角线不一定相等,而正方形的对角线一定相等.
故选:B.
A3、(2020春 江阴市校级月考)如图,四边形ABCD中,AC、BD交于点O,则根据下列条件能判定它是正方形的是( )
A.∠DAB=90°且AD=BC B.AB=BC且AC=BD
C.∠DAB=90°且AC⊥BD D.AC⊥BD且AO=BO=CO=DO
【思路点拨】根据正方形的判定对角线相等且互相垂直平分是正方形对各个选项进行分析从而得到答案.
【答案】解:A,不能判定它是正方形;
B,不能判定它是正方形;
C,不能判定它是正方形;
D,能,因为对角线相等且互相垂直平分;
故选:D.
A4、四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
【答案】A
【分析】
根据正方形的性质以及判定定理对各项进行分析即可.
【详解】
A. OA=OB=OC=OD,AC⊥BD,能判定;
B. AB∥CD,AC=BD,不能判定;
C. AD∥BC,∠A=∠C,不能判定;
D. OA=OC,OB=OD,AB=BC,不能判定;
故答案为:A.
A5、如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则∠CDE的度数为( )
A.20° B.22.5° C.25° D.30°
解:∵四边形ABCD是正方形,
∴AB=AD,∠ADC=90°,∠DAC=45°,
∵AE=AB,
∴AD=AE,
∴∠ADE=∠AED=67.5°,
∴∠CDE=90°﹣67.5°=22.5°,
故选:B.
A6、如图,把含30°的直角三角板PMN放置在正方形ABCD中,,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则的度数为( )
A.60° B.65° C.75° D.80°
【答案】C
【分析】本题考查了正方形的性质和直角三角形的性质、等腰三角形的性质,解题关键是熟练运用相关性质,根据角的关系进行计算.
根据斜边中线等于斜边一半,求出∠MPO=30°,再求出∠MOB和∠OMB的度数,即可求出的度数.
【详解】
解:∵四边形ABCD是正方形中,∴∠MBO=∠NDO=45°,
∵点O为MN的中点∴OM=ON,
∵∠MPN=90°,∴OM=OP,∴∠PMN=∠MPO=30°,
∴∠MOB=∠MPO+∠PMN =60°,
∴∠BMO=180°-60°-45°=75°,,
故选:C.
A7、如图,正方形ABCD中,点E、F分别在BC、CD上,且△AEF是等边三角形.求证:CE=CF.
证明:∵四边形ABCD是正方形,∴AD=AB,∠D=∠B=90°,
∵△AEF是等边三角形,∴AF=AE,
在Rt△ADF和Rt△ABE中,,
∴Rt△ADF≌Rt△ABE(HL),∴DF=BE,∴CE=CF.
A8、如图,AC为正方形ABCD的对角线,E为AC上一点,且AE=AB,过E作EF⊥AC,交BC于点F.
求证:BF=EF.
【分析】本题考查正方形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
如图连接AF.利用“HL”证明△AFE≌△AFB即可解决问题.
【详解】
解:如图连接AF.
∵四边形ABCD是正方形,且FE⊥AC,∴∠AEF=∠B=90°,
在Rt△AFE和Rt△AFB中,,
∴Rt△AFE≌Rt△AFB(HL),∴BF=EF.
A9、如图,在正方形中,点E在边的延长线上,点F在边的延长线上,且连接 和相交于点M.求证:.
【分析】本题考查正方形的性质,全等三角形的判定和性质等知识.掌握三角形全等的判定条件是解答本题的关键.
由题意易得出,即易证,推出.由,即可推出,即得到,从而证明了.
【详解】
证明:∵四边形ABCD是正方形,,∴,
∴在和中,,∴.∴,
∵,
∴,即,
∴,∴.
A10、已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F
(1)求证:△AEF≌△DEB;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【答案】(1)见解析;(2)当AB=AC时,四边形ADCF是正方形,见解析
【分析】此题考查全等三角形的判定,全等三角形的性质以及菱形的判定,正方形的判定,关键是根据全等三角形的判定和性质以及正方形的判定解答.
(1)根据全等三角形的判定解答即可;
(2)由全等三角形的性质和菱形的判定四边形ADCF是菱形,根据正方形的判定解答即可.
【详解】
证明:(1)∵AF∥BC,∴∠AFE=∠DBE,
∵E是AD的中点,D是BC的中点,∴AE=DE,BD=CD,
在△AEF和△DEB中,,∴△AEF≌△DEB(AAS);
(2)当AB=AC时,四边形ADCF是正方形,
理由:由(1)知,△AEF≌△DEB,则AF=DB,
∵DB=DC,∴AF=CD,
∵AF∥BC,∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,∴AD=DC=BC,∴四边形ADCF是菱形;
∵AB=AC,D是BC的中点,∴AD⊥BC,∴菱形ADCF是正方形.
【B培优综合】
B11、(2020春 西湖区校级月考)如图,正方形ABCD的边长为4,点E,F在对角线BD上,四边形AECF是菱形,且∠DAE=67.5°,则BE的长为( )
A. B.2 C.4﹣4 D.6﹣4
【思路点拨】本题考查了正方形的性质,主要利用了正方形的对角线平分一组对角,等角对等边的性质,正方形的对角线与边长的关系,等腰直角三角形的性质.
根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE.
【答案】解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠DAE=67.5°,∴在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,
∴∠DAE=∠AED,∴AD=DE=4,
∵正方形的边长为4,∴BD=4,∴BE=BD﹣DE=4﹣4.
故选:C.
B12、如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O做ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.
【答案】C
【分析】本题考查正方形的性质、全等三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.
先证明,再证明四边形MOND的面积等于,的面积,继而解得正方形的面积,据此解题.
【详解】
解:在正方形ABCD中,对角线BD⊥AC,
又
四边形MOND的面积是1,
正方形ABCD的面积是4,,
故选:C.
B13、如图,在正方形ABCD中,E为CD上的一点,连接BE,若∠EBC=20°,将△EBC绕点C按顺时针方向旋转90°得到△FDC,连接EF,则∠EFD的度数为( )
A.15° B.20° C.25° D.30°
【答案】C
【分析】本题考查旋转的性质,理解旋转变化的基本性质是解题关键.
根据旋转的性质得到∠EBC=∠FDC,CE=CF,结合三角形的外角定理求解即可.
【详解】
由旋转得:∠EBC=∠FDC=20°,CE=CF,
∵∠ECF=90°,
∴△CEF是等腰直角三角形,∠CEF=45°,
根据三角形的外角定理得:∠EFD=∠CEF-∠FDC=45°-20°=25°,
故选:C.
B14、已知平行四边形ABCD,对角线AC、BD相交于点O,且CA=CB,延长BC至点E,使CE=BC,连接DE.
(1)当AC⊥BD时,求证:BE=2CD;
(2)当∠ACB=90°时,求证:四边形ACED是正方形.
【分析】本题考查了正方形的判定,平行四边形的性质,菱形的判定和性质,熟练掌握各定理是解题的关键.
(1)根据已知条件得到四边形ABCD是菱形.求得BC=CD.得到BE=2BC,于是得到结论;
(2)根据平行四边形的性质得到AD=BC,AD∥BE,求得AD=CE,AD∥CE,推出平行四边形ACED是矩形,根据正方形的判定定理即可得到结论.
【详解】
(1)证明:∵四边形ABCD是平行四边形,
又∵AC⊥BD,∴四边形ABCD是菱形.∴BC=CD.
又∵CE=BC,∴BE=2BC,∴BE=2CD;
(2)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BE,
又∵CE=BC,∴AD=CE,AD∥CE,
∴四边形ACED是平行四边形.
∵∠ACB=90°,∴平行四边形ACED是矩形,
又∵CA=CB,∴CA=CE,∴矩形ACED是正方形.
B15、(2020春 常州期末)如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
【点拨】(1)根据正方形的性质和菱形的判定解答即可;
(2)根据正方形和菱形的性质以及勾股定理解答即可.
【解析】(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,AC⊥BD.
∵BE=DF,∴OB+BE=OD+DF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,∴AO=AC,BO=BD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB==3,∴AO=BO=3.∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE===3.
∵四边形AECF是菱形,∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.∴四边形AECF的周长是12.
B16、(2020春 拱墅区期末)如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
【思路点拨】(1)由“SAS”可证△ABG≌△CBG,可得AG=CG,∠BAG=∠BCG,由四边形内角和定理可证∠BCG=∠GFC,可得GC=GF=AG;
(2)过点G作GH⊥BC于H,利用勾股定理可求GH的长,即可求解;
(3)在AB上截取BF=BN,连接NF,由“HL”可证Rt△ABF≌Rt△ADE,可得∠BAF=∠DAE=22.5°,BF=DE,可得FC=BF,即可求解.
【答案】证明:(1)连接GC,
∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,∠ABD=∠CBD=45°,
又∵BG=BG,∴△ABG≌△CBG(SAS),∴AG=CG,∠BAG=∠BCG,
∵∠ABC+∠BAG+∠AGF+∠BFG=360°,且∠ABC=∠AGF=90°,
∴∠BAG+∠BFG=180°,∴∠BCG+∠BFG=180°,
∵∠BFG+∠GFC=180°,∴∠BCG=∠GFC,
∴GC=GF,∴AG=FG;
(2)如图2,过点G作GH⊥BC于H,
∵AB=10,BF=4,∴AF2=AB2+BF2=AG2+GF2,∴GF2=58,
∵∠DBC=45°,GH⊥BC,∴BH=GH,BG=GH,
∵GF2=GH2+FH2,∴58=GH2+(GH﹣4)2,
∴GH=7,(负值舍去),∴BG=7;
(3)如图,在AB上截取BF=BN,连接NF,
∵AG=GF,AG⊥GF,∴∠EAF=45°,
∵AE=AF,AB=AD,∴Rt△ABF≌Rt△ADE(HL),
∴∠BAF=∠DAE=22.5°,BF=DE,∴CF=CE,
∵BF=BN,∠ABC=90°,∴NF=BF,∠BNF=∠BFN=45°,
∴∠BAF=∠AFN=22.5°,∴AN=NF=BF,
∵AB=BC,∴BN+AN=BF+FC,∴FC=BF,∴BC=(+1)BF,
∴正方形ABCD与△CEF的面积之比=BC2:FC2=3+2:1.
【C拔尖拓展】
C17、如图,以边长为4的正方形ABCD的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于E、F两点,则线段EF的最小值为( )
A.2 B.4 C. D.2
解:如图,连接EF,
∵四边形ABCD为正方形,∴∠EAO=∠FDO=45°,AO=DO;
∵∠EOF=90°,∠AOD=90°,∴∠AOE=∠DOF;
在△AOE与△DOF中,,∴△AOE≌△DOF(ASA),
∴OE=OF(设为λ);∴△EOF是等腰直角三角形,
由勾股定理得:EF2=OE2+OF2=2λ2;∴EF=OE=λ,
∵正方形ABCD的边长是4,
∴OA=2,O到AB的距离等于2(O到AB的垂线段的长度),
由题意可得:2≤λ≤2,
∴2≤EF≤4.所以线段EF的最小值为2.
故选:D.
C18、(1)尝试探究:
如图1,是正方形的边上的一点,过点作,交的延长线于.
①求证:;
②过点作的平分线交于,连结,请探究与的数量关系,
并证明你的结论.
(2)拓展应用:
如图2,是正方形的边上的一点,过点作,交的延长线于,连结交于,连结并延长交于,已知,求的长.
【分析】 本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
(1)①先判断出∠CBF=90°,再证明∠DCE=∠BCF即可解决问题.
②证明△PCE≌△PCF(SAS)即可解决问题.
(2)如图2中,作EH⊥AD交BD于H,连接PE.证明△EMH≌△FMB(AAS),由EM=FM,CE=CF,推出PC垂直平分线段EF,推出PE=PF,设PB=x,则PE=PF=x+2,PA=6-x,理由勾股定理构建方程即可解决问题.
解:(1)①如图1中,在正方形ABCD中,DC=BC,∠D=∠ABC=∠DCB=90°,
∴∠CBF=180°-∠ABC=90°,
∵CF⊥CE,∴∠ECF=90°,∴∠DCB=∠ECF=90°,∴∠DCE=∠BCF,
∴△CDE≌△CBF(ASA).
②结论:PE=PF.
理由:如图1中,∵△CDE≌△CBF,∴CE=CF,
∵PC=PC,∠PCE=∠PCF,∴△PCE≌△PCF(SAS),∴PE=PF.
(2)如图2中,作EH⊥AD交BD于H,连接PE.
∵四边形ABCD是正方形,∴AB=AD=6,∠A=90°,∠EDH=45°,
∵EH⊥AD,∴∠DEH=∠A=90°,∴EH∥AF,DE=EH=2,
∵△CDE≌△CBF,∴DE=BF=2,∴EH=BF,
∵∠EHM=∠MBF,∠EMH=∠FMB,∴△EMH≌△FMB(AAS),
∵EM=FM,
∵CE=CF,∴PC垂直平分线段EF, ∴PE=PF,设PB=x,则PE=PF=x+2,PA=6-x,
在Rt△APE中,则有(x+2)2=42+(6-x)2,
∴x=3,∴PB=3.
-2021-2022学年八年级数学下册 (苏科版)
【A夯实基础】
A1、已知正方形ABCD对角线AC,BD相交于点O,且AC=16cm,
则DO=_______cm,BO=______cm,∠OCD=_______度.
A2、(2020春 阿城区期末)正方形具有而菱形不具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线平分一组对角 D.对角线互相垂直
A3、(2020春 江阴市校级月考)如图,四边形ABCD中,AC、BD交于点O,则根据下列条件能判定它是正方形的是( )
A.∠DAB=90°且AD=BC B.AB=BC且AC=BD
C.∠DAB=90°且AC⊥BD D.AC⊥BD且AO=BO=CO=DO
A4、四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
A5、如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则∠CDE的度数为( )
A.20° B.22.5° C.25° D.30°
A6、如图,把含30°的直角三角板PMN放置在正方形ABCD中,,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则的度数为( )
A.60° B.65° C.75° D.80°
A7、如图,正方形ABCD中,点E、F分别在BC、CD上,且△AEF是等边三角形.求证:CE=CF.
A8、如图,AC为正方形ABCD的对角线,E为AC上一点,且AE=AB,过E作EF⊥AC,交BC于点F.
求证:BF=EF.
A9、如图,在正方形中,点E在边的延长线上,点F在边的延长线上,且连接 和相交于点M.求证:.
A10、已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F
(1)求证:△AEF≌△DEB;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【B培优综合】
B11、(2020春 西湖区校级月考)如图,正方形ABCD的边长为4,点E,F在对角线BD上,四边形AECF是菱形,且∠DAE=67.5°,则BE的长为( )
A. B.2 C.4﹣4 D.6﹣4
B12、如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O做ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.
B13、如图,在正方形ABCD中,E为CD上的一点,连接BE,若∠EBC=20°,将△EBC绕点C按顺时针方向旋转90°得到△FDC,连接EF,则∠EFD的度数为( )
A.15° B.20° C.25° D.30°
B14、已知平行四边形ABCD,对角线AC、BD相交于点O,且CA=CB,延长BC至点E,使CE=BC,连接DE.
(1)当AC⊥BD时,求证:BE=2CD;
(2)当∠ACB=90°时,求证:四边形ACED是正方形.
B15、(2020春 常州期末)如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
B16、(2020春 拱墅区期末)如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
【C拔尖拓展】
C17、如图,以边长为4的正方形ABCD的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于E、F两点,则线段EF的最小值为( )
A.2 B.4 C. D.2
C18、(1)尝试探究:
如图1,是正方形的边上的一点,过点作,交的延长线于.
①求证:;
②过点作的平分线交于,连结,请探究与的数量关系,
并证明你的结论.
(2)拓展应用:
如图2,是正方形的边上的一点,过点作,交的延长线于,连结交于,连结并延长交于,已知,求的长.
9.4.3正方形-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、已知正方形ABCD对角线AC,BD相交于点O,且AC=16cm,
则DO=_______cm,BO=______cm,∠OCD=_______度.
解:∵正方形ABCD,AC=16cm
∴DO=AC=8=BO, ∠OCD=45°.
故答案为8,8,45.
A2、(2020春 阿城区期末)正方形具有而菱形不具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线平分一组对角 D.对角线互相垂直
【思路点拨】根据正方形的性质以及菱形的性质即可判断.
【答案】解:正方形和菱形都满足:四条边都相等,对角线平分一组对角,对角线垂直且互相平分;
菱形的对角线不一定相等,而正方形的对角线一定相等.
故选:B.
A3、(2020春 江阴市校级月考)如图,四边形ABCD中,AC、BD交于点O,则根据下列条件能判定它是正方形的是( )
A.∠DAB=90°且AD=BC B.AB=BC且AC=BD
C.∠DAB=90°且AC⊥BD D.AC⊥BD且AO=BO=CO=DO
【思路点拨】根据正方形的判定对角线相等且互相垂直平分是正方形对各个选项进行分析从而得到答案.
【答案】解:A,不能判定它是正方形;
B,不能判定它是正方形;
C,不能判定它是正方形;
D,能,因为对角线相等且互相垂直平分;
故选:D.
A4、四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
【答案】A
【分析】
根据正方形的性质以及判定定理对各项进行分析即可.
【详解】
A. OA=OB=OC=OD,AC⊥BD,能判定;
B. AB∥CD,AC=BD,不能判定;
C. AD∥BC,∠A=∠C,不能判定;
D. OA=OC,OB=OD,AB=BC,不能判定;
故答案为:A.
A5、如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则∠CDE的度数为( )
A.20° B.22.5° C.25° D.30°
解:∵四边形ABCD是正方形,
∴AB=AD,∠ADC=90°,∠DAC=45°,
∵AE=AB,
∴AD=AE,
∴∠ADE=∠AED=67.5°,
∴∠CDE=90°﹣67.5°=22.5°,
故选:B.
A6、如图,把含30°的直角三角板PMN放置在正方形ABCD中,,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则的度数为( )
A.60° B.65° C.75° D.80°
【答案】C
【分析】本题考查了正方形的性质和直角三角形的性质、等腰三角形的性质,解题关键是熟练运用相关性质,根据角的关系进行计算.
根据斜边中线等于斜边一半,求出∠MPO=30°,再求出∠MOB和∠OMB的度数,即可求出的度数.
【详解】
解:∵四边形ABCD是正方形中,∴∠MBO=∠NDO=45°,
∵点O为MN的中点∴OM=ON,
∵∠MPN=90°,∴OM=OP,∴∠PMN=∠MPO=30°,
∴∠MOB=∠MPO+∠PMN =60°,
∴∠BMO=180°-60°-45°=75°,,
故选:C.
A7、如图,正方形ABCD中,点E、F分别在BC、CD上,且△AEF是等边三角形.求证:CE=CF.
证明:∵四边形ABCD是正方形,∴AD=AB,∠D=∠B=90°,
∵△AEF是等边三角形,∴AF=AE,
在Rt△ADF和Rt△ABE中,,
∴Rt△ADF≌Rt△ABE(HL),∴DF=BE,∴CE=CF.
A8、如图,AC为正方形ABCD的对角线,E为AC上一点,且AE=AB,过E作EF⊥AC,交BC于点F.
求证:BF=EF.
【分析】本题考查正方形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
如图连接AF.利用“HL”证明△AFE≌△AFB即可解决问题.
【详解】
解:如图连接AF.
∵四边形ABCD是正方形,且FE⊥AC,∴∠AEF=∠B=90°,
在Rt△AFE和Rt△AFB中,,
∴Rt△AFE≌Rt△AFB(HL),∴BF=EF.
A9、如图,在正方形中,点E在边的延长线上,点F在边的延长线上,且连接 和相交于点M.求证:.
【分析】本题考查正方形的性质,全等三角形的判定和性质等知识.掌握三角形全等的判定条件是解答本题的关键.
由题意易得出,即易证,推出.由,即可推出,即得到,从而证明了.
【详解】
证明:∵四边形ABCD是正方形,,∴,
∴在和中,,∴.∴,
∵,
∴,即,
∴,∴.
A10、已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F
(1)求证:△AEF≌△DEB;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【答案】(1)见解析;(2)当AB=AC时,四边形ADCF是正方形,见解析
【分析】此题考查全等三角形的判定,全等三角形的性质以及菱形的判定,正方形的判定,关键是根据全等三角形的判定和性质以及正方形的判定解答.
(1)根据全等三角形的判定解答即可;
(2)由全等三角形的性质和菱形的判定四边形ADCF是菱形,根据正方形的判定解答即可.
【详解】
证明:(1)∵AF∥BC,∴∠AFE=∠DBE,
∵E是AD的中点,D是BC的中点,∴AE=DE,BD=CD,
在△AEF和△DEB中,,∴△AEF≌△DEB(AAS);
(2)当AB=AC时,四边形ADCF是正方形,
理由:由(1)知,△AEF≌△DEB,则AF=DB,
∵DB=DC,∴AF=CD,
∵AF∥BC,∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,∴AD=DC=BC,∴四边形ADCF是菱形;
∵AB=AC,D是BC的中点,∴AD⊥BC,∴菱形ADCF是正方形.
【B培优综合】
B11、(2020春 西湖区校级月考)如图,正方形ABCD的边长为4,点E,F在对角线BD上,四边形AECF是菱形,且∠DAE=67.5°,则BE的长为( )
A. B.2 C.4﹣4 D.6﹣4
【思路点拨】本题考查了正方形的性质,主要利用了正方形的对角线平分一组对角,等角对等边的性质,正方形的对角线与边长的关系,等腰直角三角形的性质.
根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE.
【答案】解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠DAE=67.5°,∴在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,
∴∠DAE=∠AED,∴AD=DE=4,
∵正方形的边长为4,∴BD=4,∴BE=BD﹣DE=4﹣4.
故选:C.
B12、如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O做ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.
【答案】C
【分析】本题考查正方形的性质、全等三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.
先证明,再证明四边形MOND的面积等于,的面积,继而解得正方形的面积,据此解题.
【详解】
解:在正方形ABCD中,对角线BD⊥AC,
又
四边形MOND的面积是1,
正方形ABCD的面积是4,,
故选:C.
B13、如图,在正方形ABCD中,E为CD上的一点,连接BE,若∠EBC=20°,将△EBC绕点C按顺时针方向旋转90°得到△FDC,连接EF,则∠EFD的度数为( )
A.15° B.20° C.25° D.30°
【答案】C
【分析】本题考查旋转的性质,理解旋转变化的基本性质是解题关键.
根据旋转的性质得到∠EBC=∠FDC,CE=CF,结合三角形的外角定理求解即可.
【详解】
由旋转得:∠EBC=∠FDC=20°,CE=CF,
∵∠ECF=90°,
∴△CEF是等腰直角三角形,∠CEF=45°,
根据三角形的外角定理得:∠EFD=∠CEF-∠FDC=45°-20°=25°,
故选:C.
B14、已知平行四边形ABCD,对角线AC、BD相交于点O,且CA=CB,延长BC至点E,使CE=BC,连接DE.
(1)当AC⊥BD时,求证:BE=2CD;
(2)当∠ACB=90°时,求证:四边形ACED是正方形.
【分析】本题考查了正方形的判定,平行四边形的性质,菱形的判定和性质,熟练掌握各定理是解题的关键.
(1)根据已知条件得到四边形ABCD是菱形.求得BC=CD.得到BE=2BC,于是得到结论;
(2)根据平行四边形的性质得到AD=BC,AD∥BE,求得AD=CE,AD∥CE,推出平行四边形ACED是矩形,根据正方形的判定定理即可得到结论.
【详解】
(1)证明:∵四边形ABCD是平行四边形,
又∵AC⊥BD,∴四边形ABCD是菱形.∴BC=CD.
又∵CE=BC,∴BE=2BC,∴BE=2CD;
(2)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BE,
又∵CE=BC,∴AD=CE,AD∥CE,
∴四边形ACED是平行四边形.
∵∠ACB=90°,∴平行四边形ACED是矩形,
又∵CA=CB,∴CA=CE,∴矩形ACED是正方形.
B15、(2020春 常州期末)如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
【点拨】(1)根据正方形的性质和菱形的判定解答即可;
(2)根据正方形和菱形的性质以及勾股定理解答即可.
【解析】(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,AC⊥BD.
∵BE=DF,∴OB+BE=OD+DF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,∴AO=AC,BO=BD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB==3,∴AO=BO=3.∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE===3.
∵四边形AECF是菱形,∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.∴四边形AECF的周长是12.
B16、(2020春 拱墅区期末)如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
【思路点拨】(1)由“SAS”可证△ABG≌△CBG,可得AG=CG,∠BAG=∠BCG,由四边形内角和定理可证∠BCG=∠GFC,可得GC=GF=AG;
(2)过点G作GH⊥BC于H,利用勾股定理可求GH的长,即可求解;
(3)在AB上截取BF=BN,连接NF,由“HL”可证Rt△ABF≌Rt△ADE,可得∠BAF=∠DAE=22.5°,BF=DE,可得FC=BF,即可求解.
【答案】证明:(1)连接GC,
∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,∠ABD=∠CBD=45°,
又∵BG=BG,∴△ABG≌△CBG(SAS),∴AG=CG,∠BAG=∠BCG,
∵∠ABC+∠BAG+∠AGF+∠BFG=360°,且∠ABC=∠AGF=90°,
∴∠BAG+∠BFG=180°,∴∠BCG+∠BFG=180°,
∵∠BFG+∠GFC=180°,∴∠BCG=∠GFC,
∴GC=GF,∴AG=FG;
(2)如图2,过点G作GH⊥BC于H,
∵AB=10,BF=4,∴AF2=AB2+BF2=AG2+GF2,∴GF2=58,
∵∠DBC=45°,GH⊥BC,∴BH=GH,BG=GH,
∵GF2=GH2+FH2,∴58=GH2+(GH﹣4)2,
∴GH=7,(负值舍去),∴BG=7;
(3)如图,在AB上截取BF=BN,连接NF,
∵AG=GF,AG⊥GF,∴∠EAF=45°,
∵AE=AF,AB=AD,∴Rt△ABF≌Rt△ADE(HL),
∴∠BAF=∠DAE=22.5°,BF=DE,∴CF=CE,
∵BF=BN,∠ABC=90°,∴NF=BF,∠BNF=∠BFN=45°,
∴∠BAF=∠AFN=22.5°,∴AN=NF=BF,
∵AB=BC,∴BN+AN=BF+FC,∴FC=BF,∴BC=(+1)BF,
∴正方形ABCD与△CEF的面积之比=BC2:FC2=3+2:1.
【C拔尖拓展】
C17、如图,以边长为4的正方形ABCD的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于E、F两点,则线段EF的最小值为( )
A.2 B.4 C. D.2
解:如图,连接EF,
∵四边形ABCD为正方形,∴∠EAO=∠FDO=45°,AO=DO;
∵∠EOF=90°,∠AOD=90°,∴∠AOE=∠DOF;
在△AOE与△DOF中,,∴△AOE≌△DOF(ASA),
∴OE=OF(设为λ);∴△EOF是等腰直角三角形,
由勾股定理得:EF2=OE2+OF2=2λ2;∴EF=OE=λ,
∵正方形ABCD的边长是4,
∴OA=2,O到AB的距离等于2(O到AB的垂线段的长度),
由题意可得:2≤λ≤2,
∴2≤EF≤4.所以线段EF的最小值为2.
故选:D.
C18、(1)尝试探究:
如图1,是正方形的边上的一点,过点作,交的延长线于.
①求证:;
②过点作的平分线交于,连结,请探究与的数量关系,
并证明你的结论.
(2)拓展应用:
如图2,是正方形的边上的一点,过点作,交的延长线于,连结交于,连结并延长交于,已知,求的长.
【分析】 本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
(1)①先判断出∠CBF=90°,再证明∠DCE=∠BCF即可解决问题.
②证明△PCE≌△PCF(SAS)即可解决问题.
(2)如图2中,作EH⊥AD交BD于H,连接PE.证明△EMH≌△FMB(AAS),由EM=FM,CE=CF,推出PC垂直平分线段EF,推出PE=PF,设PB=x,则PE=PF=x+2,PA=6-x,理由勾股定理构建方程即可解决问题.
解:(1)①如图1中,在正方形ABCD中,DC=BC,∠D=∠ABC=∠DCB=90°,
∴∠CBF=180°-∠ABC=90°,
∵CF⊥CE,∴∠ECF=90°,∴∠DCB=∠ECF=90°,∴∠DCE=∠BCF,
∴△CDE≌△CBF(ASA).
②结论:PE=PF.
理由:如图1中,∵△CDE≌△CBF,∴CE=CF,
∵PC=PC,∠PCE=∠PCF,∴△PCE≌△PCF(SAS),∴PE=PF.
(2)如图2中,作EH⊥AD交BD于H,连接PE.
∵四边形ABCD是正方形,∴AB=AD=6,∠A=90°,∠EDH=45°,
∵EH⊥AD,∴∠DEH=∠A=90°,∴EH∥AF,DE=EH=2,
∵△CDE≌△CBF,∴DE=BF=2,∴EH=BF,
∵∠EHM=∠MBF,∠EMH=∠FMB,∴△EMH≌△FMB(AAS),
∵EM=FM,
∵CE=CF,∴PC垂直平分线段EF, ∴PE=PF,设PB=x,则PE=PF=x+2,PA=6-x,
在Rt△APE中,则有(x+2)2=42+(6-x)2,
∴x=3,∴PB=3.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
