2021—2022学年苏科版数学八年级下册第9章中心对称图形—平行四边形单元综合练习题(培优)(Word版含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级下册第9章中心对称图形—平行四边形单元综合练习题(培优)(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 982.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 00:00:00 | ||
图片预览

文档简介
第9章 中心对称图形—平行四边形 单元综合练习题(培优)
2021-2022学年苏科版七年级数学下册
一、选择题
1、下列标志既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2、矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B. 对角线相等
C.对角线互相平分 D. 两组对角分别相等
3、如图,菱形ABCD的边长为4,过点A、C作对角线AC的垂线,分别交CB和AD的延长线于点E、F,AE=3,则四边形AECF的周长为( )
A. 22 B. 18 C. 14 D. 11
4、如图,在 ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
5、如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD=( )
A.3 B.4 C.4.8 D.5
6、如图,正方形的面积为256,点F在上,点E在的延长线上,的面积为200,则的长为( )
A.10 B.11 C.12 D.15
7、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A. 2.5 B. C. D. 2
8、如图,在平行四边形中,,是锐角,于点,是的中点,连接;若,则的长为( )
A. B. C. D.
9、(泰州海陵区、医药高新区联考20-21八下期末)如图,边长为定值的正方形ABCD的中心与正方形EFGH的顶点重合,且与边BC、AB相交于M、N,图中阴影部分的面积记为S,两条线段MB、BN的长度之和记为l,将正方形 EFGH绕点E逆时针旋转适当角度,则有( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
10、如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①∠EFH=45°;②△AHD≌△EHF;③∠AEF+∠HAD=45°; ④若=2,则.其中结论正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
11、(南京浦口区第三中学21-22八上12月月考)如图,平行四边形ABCD,AD=5,AB=8,点A的坐标为(-3,0)点C的坐标为______.
12、(2021春 昆明期末)如图,某小区要在一块矩形的空地上建造一个如图所示的四边形花园,点,,,分别为边,,,的中点,若,,则四边形的面积为 .
13、如图,将边长为的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE= .
14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数= 度.
15、在四边形ABCD中,对角线AC⊥BD且AC=6、BD=8,E、F分别是边AB、CD的中点,则EF= .
16、已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
17、(2022·江苏·)已知如图,在矩形ABCD中,点E、F分别是AD、BC上一点,将四边形ABFE沿着EF折叠,点B恰好与点D重合,点A与点A'重合,∠A'DC的角平分线交EF于点O,若AE=5,BF=13,则OD=_____.
18、(2022·广东·重庆巴蜀中学九年级开学考试)如图,F为正方形ABCD的边CD上一动点,AB=2,连接BF,过A作AH⊥BF交BC于H,交BF于G,连接CG,当CG为最小值时,CH的长为 _____.
三、解答题
19、如图,△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣4,1),C(﹣1,2).
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,写出B2和C2的坐标;
(3)直接写出△ABC绕原点O顺时针旋转一周扫过的图形面积.
20、如图,点在外,连接,,延长交于,为的中点.
(1)求证:;
(2)若,,,,求的长.
21、已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在对角线AC上,且BF=DE,AH=CG,连接FH、HE、BG、FG.
(1)求证:FG=EH.
(2)若EG平分∠AEH,FH平分∠CFG,FG//AB,∠ACD=68°,∠GFH=35°,求∠GHF的度数.
22、已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
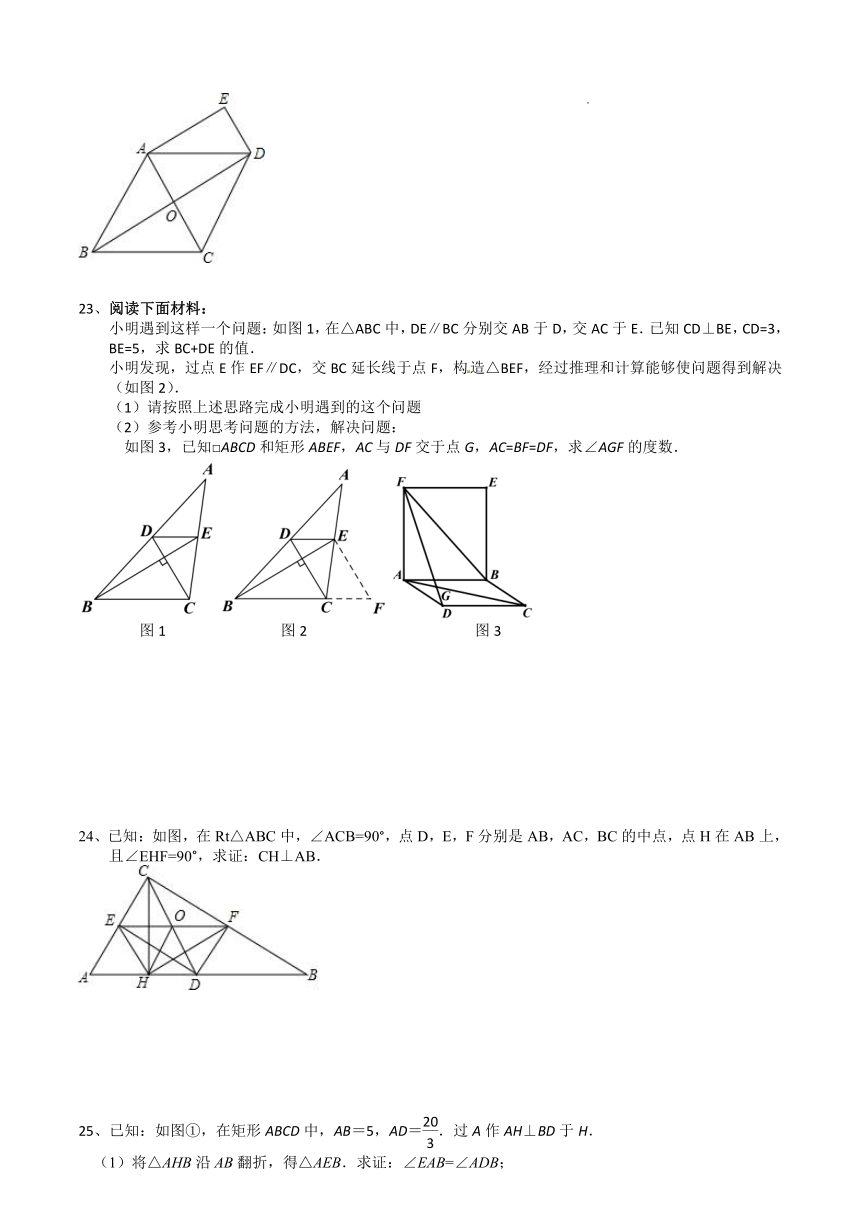
23、阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
图1 图2 图3
24、已知:如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别是AB,AC,BC的中点,点H在AB上,且∠EHF=90°,求证:CH⊥AB.
25、已知:如图①,在矩形ABCD中,AB=5,AD=.过A作AH⊥BD于H.
(1)将△AHB沿AB翻折,得△AEB.求证:∠EAB=∠ADB;
(2)如图②,将△ABE绕点B顺时针旋转,记旋转中的△ABE为△A′BE′,在旋转过程中,延长A′E′与对角线BD交于点Q,与边AD交于点P,问是否存在这样的Q、P两点,使△DQP为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
26、(2020秋 永年区期中)(1)如图1,点、分别在正方形的边、上,,求证:;
(2)如图2,四边形中,,,,点、分别在边、 上,则当与满足什么关系时,仍有,说明理由.
27、如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
第9章 中心对称图形—平行四边形 单元综合练习题(培优)
2021-2022学年苏科版七年级数学下册(解析)
一、选择题
1、下列标志既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
分析: 掌握中心对称图形与轴对称图形的概念,要注意:轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
根据轴对称图形与中心对称图形的概念求解.
解答: 解:A、是轴对称图形,也是中心对称图形,故A选项符合题意;
B、是轴对称图形,不是中心对称图形,故B选项不符合题意;
C、不是轴对称图形,是中心对称图形,故C选项不符合题意;
D、是轴对称图形,不是中心对称图形,故D选项不符合题意.
故选A.
2、矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B. 对角线相等
C.对角线互相平分 D. 两组对角分别相等
分析: 根据矩形与菱形的性质对各选项分析判断后利用排除法求解.
解答: 解:A、矩形与菱形的两组对边都分别平行,故本选项错误;
B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;
C、矩形与菱形的对角线都互相平分,故本选项错误;
D、矩形与菱形的两组对角都分别相等,故本选项错误.
故选B.
3、如图,菱形ABCD的边长为4,过点A、C作对角线AC的垂线,分别交CB和AD的延长线于点E、F,AE=3,则四边形AECF的周长为( )
A. 22 B. 18 C. 14 D. 11
分析:本题考查了菱形的对角线平分一组对角的性质,等角的余角相等的性质,平行四边形的判定与性质,熟记性质并求出EC的长度是解题的关键.
根据菱形的对角线平分一组对角可得∠BAC=∠BCA,再根据等角的余角相等求出∠BAE=∠E,根据等角对等边可得BE=AB,然后求出EC,同理可得AF,然后判断出四边形AECF是平行四边形,再根据周长的定义列式计算即可得解.
解答: 解:在菱形ABCD中,∠BAC=∠BCA,
∵AE⊥AC,
∴∠BAC+∠BAE=∠BCA+∠E=90°,
∴∠BAE=∠E,
∴BE=AB=4,
∴EC=BE+BC=4+4=8,
同理可得AF=8,
∵AD∥BC,
∴四边形AECF是平行四边形,
∴四边形AECF的周长=2(AE+EC)=2(3+8)=22.
故选:A.
4、如图,在 ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
【答案】C
【分析】此题主要考查了平行四边形的性质和角平分线的性质,勾股定理的逆定理,勾股定理,关键是掌握平行四边形对边平行且相等.
根据平行四边形的性质和角平分线的定义可得AD=BC=EB=5,根据勾股定理的逆定理可得∠AED=90°,再根据平行四边形的性质可得CD=AB=8,∠EDC=90°,根据勾股定理可求CE的长.
【解析】
解:∵CE平分∠BCD,∴∠BCE=∠DCE,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠BEC=∠DCE,∴∠BEC=∠BCE,
∴BC=BE=5,∴AD=5,
∵EA=3,ED=4,
在△AED中,32+42=52,即EA2+ED2=AD2,
∴∠AED=90°,
∴CD=AB=3+5=8,∠EDC=90°,
在Rt△EDC中,CE===4.
故选:C.
5、如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD=( )
A.3 B.4 C.4.8 D.5
【答案】D
【分析】
由勾股定理逆定理易证为直角三角形.又由DE垂直平分AC,易证∠AED=90°,AE=CE=4,即可推出DE是△ABC的中位线,即求出DE=BC=3,最后在中,利用勾股定理即可求出CD的长.
【解析】
∵AB=10,BC=6,AC=8,∴,∴∠ACB=90°,
∵DE垂直平分AC,
∴∠AED=90°,AE=CE=4,∴DE∥BC,
∴DE是△ABC的中位线,∴DE=BC=3.
在中,.
6、如图,正方形的面积为256,点F在上,点E在的延长线上,的面积为200,则的长为( )
A.10 B.11 C.12 D.15
【答案】C
【分析】本题考查了正方形,等腰直角三角形面积的计算,考查了直角三角形中勾股定理的运用,本题中求证CF=CE是解题的关键.
先证明Rt△CDF≌Rt△CBE,故CE=CF,根据△CEF的面积计算CE,根据正方形ABCD的面积计算BC,根据勾股定理计算BE.
【详解】
解:∵∠ECF=90°,∠DCB=90°,
∴∠BCE=∠DCF,∴,∴△CDF≌△CBE,故CF=CE.
因为Rt△CEF的面积是200,即 CE CF=200,故CE=20,
正方形ABCD的面积=BC2=256,得BC=16.根据勾股定理得:BE==12.
故选:C.
7、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A. 2.5 B. C. D. 2
分析: 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,正方形的性质,勾股定理,熟记各性质并作辅助线构造出直角三角形是解题的关键.
连接AC、CF,根据正方形性质求出AC、CF,∠ACD=∠GCF=45°,再求出∠ACF=90°,然后利用勾股定理列式求出AF,再根据直角三角形斜边上的中线等于斜边的一半解答即可.
解答: 解:如图,连接AC、CF,
∵正方形ABCD和正方形CEFG中,BC=1,CE=3,
∴AC=,CF=3,
∠ACD=∠GCF=45°,
∴∠ACF=90°,
由勾股定理得,AF===2,
∵H是AF的中点,
∴CH=AF=×2=.
故选:B.
8、如图,在平行四边形中,,是锐角,于点,是的中点,连接;若,则的长为( )
A. B. C. D.
【答案】B
【分析】
延长EF,DA交于G,连接DE,先证明△AFG≌△BFE,进而得到BE=AG,F是GE的中点,结合条件BF⊥GE进而得到BF是线段GE的垂直平分线,得到GD=DE,最后在Rt△AED中使用勾股定理即可求解.
【解析】
解:延长EF,DA交于G,连接DE,如下图所示:
∵F是AB的中点,∴AF=BF,
∵四边形ABCD是平行四边形,
∴AB∥BC,∴∠GAB=∠EBF
且∠GFA=∠EFB,∴△AFG≌△BFE(ASA),
设,
由GF=EF,且∠DFE=90°知,
DF是线段GE的垂直平分线,
∴,
在Rt△BAE中,.
在Rt△AED中,,
∴,解得,
∴,
故选:B.
9、(泰州海陵区、医药高新区联考20-21八下期末)如图,边长为定值的正方形ABCD的中心与正方形EFGH的顶点重合,且与边BC、AB相交于M、N,图中阴影部分的面积记为S,两条线段MB、BN的长度之和记为l,将正方形 EFGH绕点E逆时针旋转适当角度,则有( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
【答案】D
【解析】
【分析】本题考了全等三角形的判定和性质,正确寻找全等三角形是解题的关键.
如图,连接,,可证明,可得 ,根据,是一个定值,,也是一个定值,可得结论.
【详解】
解:如图,连接,.
∵边长为定值的正方形ABCD的中心与正方形EFGH的顶点重合,
即点E是正方形ABCD的中心,
∴,,
又∵,∴,∴
在和中,,∴,∴,
∴,是一个定值,,也是一个定值,即:与均不变,
故选:.
10、如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①∠EFH=45°;②△AHD≌△EHF;③∠AEF+∠HAD=45°; ④若=2,则.其中结论正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
【答案】A
【分析】①根据正方形的性质证明∠ADB=45°,进而得△DFG为等腰直角三角形,根据等腰三角形的三线合一性质得∠EFH=∠EFD=45°,故①正确;
②根据矩形性质得AF=EB,∠BEF=90°,再证明△AFH≌△EGH得EH=AH,进而证明△EHF≌△AHD,故②正确;
③由△EHF≌△AHD得∠EHF=∠AHD,怀AH=EH得∠AEF+∠HEF=45°,进而得∠AEF+∠HAD=45°,故③正确;
④如图,过点H作MN⊥AD于点M,与BC交于点N,设EC=FD=FG=x,则BE=AF=EG=2x,BC=DC=AB=AD=3x,HM=x,AM=x,HN=x,由勾股定理得AH2,再由三角形的面积公式得,便可判断④的正误,
【解答】证明:①在正方形ABCD中,∠ADC=∠C=90°,∠ADB=45°,
∵EF∥CD,∴∠EFD=90°,∴四边形EFDC是矩形.
在Rt△FDG中,∠FDG=45°,∴FD=FG,
∵H是DG中点,∴∠EFH=∠EFD=45°故①正确;
②∵四边形ABEF是矩形,∴AF=EB,∠BEF=90°,
∵BD平分∠ABC,∴∠EBG=∠EGB=45°,∴BE=GE,∴AF=EG.
在Rt△FGD中,H是DG的中点,∴FH=GH,FH⊥BD,
∵∠AFH=∠AFE+∠GFH=90°+45°=135°,
∠EGH=180°﹣∠EGB=180°﹣45°=135°,
∴∠AFH=∠EGH,∴△AFH≌△EGH(SAS),∴EH=AH,
∵EF=AD,FH=DH,∴△EHF≌△AHD(SSS),故②正确;
③∵△EHF≌△AHD,∴∠EHF=∠AHD,∴∠AHE=∠DHF=90°,
∵AH=EH,∴∠AEH=45°,即∠AEF+∠HEF=45°,
∵∠HEF=∠HAD,∴∠AEF+∠HAD=45°,故③正确;
④如图,过点H作MN⊥AD于点M,与BC交于点N,
设EC=FD=FG=x,则BE=AF=EG=2x,
∴BC=DC=AB=AD=3x,HM=x,AM=x,HN=x,
∴AH2=,∴=,故④错误;
故选:A.
二、填空题
11、(南京浦口区第三中学21-22八上12月月考)如图,平行四边形ABCD,AD=5,AB=8,点A的坐标为(-3,0)点C的坐标为______.
【答案】(8,4)
【分析】本题考查平行四边形性质,勾股定理,平行x轴两点坐标特征,解答本题的关键是熟练掌握平行于x轴的直线上的点的纵坐标相同,平行于y轴的直线上的点的横坐标相同.
先根据勾股定理得到OD的长,即可得到点D的坐标,再根据平行四边形的性质和平行x轴两点坐标特征即可得到点C的坐标.
【详解】
解:∵点A的坐标为(-3,0),
在Rt△ADO中,AD=5, AO=3,,∴OD==,∴D(0,4),
∵平行四边形ABCD,∴AB=CD=8,AB∥CD,
∵AB在x轴上,∴CD∥x轴,
∴C、D两点的纵坐标相同,∴C(8,4) .
故答案为(8,4).
12、(2021春 昆明期末)如图,某小区要在一块矩形的空地上建造一个如图所示的四边形花园,点,,,分别为边,,,的中点,若,,则四边形的面积为 .
【分析】根据矩形的性质推出,得到平行四边形,推出,,同理得到,,推出,根据三角形的面积公式求出即可.
【解析】连接、,
四边形是矩形,,,
、分别为边、的中点,,
四边形是平行四边形,,,
同理,,
,,
四边形的面积是.
故答案为:100.
13、如图,将边长为的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE= .
【分析】计算题.本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.
根据正方形的性质得AC=(2+)=2+2,∠ACD=∠BAC=45°,再利用旋转的性质得∠BAB′=45°,AB′=AB=2+,∠AB′C′=∠B=90°,于是可判断点B′在AC上,所以CB′=AC﹣AB′=,然后利用△ECB′为等腰直角三角形易得CE=CB′=2.
【解答】解:∵四边形ABCD为正方形,
∴AC=(2+)=2+2,∠ACD=∠BAC=45°,
∵正方形ABCD绕点A逆时针方向旋转45°至正方形AB′C′D′,
∴∠BAB′=45°,AB′=AB=2+,∠AB′C′=∠B=90°,
∴点B′在AC上,∴CB′=AC﹣AB′=2+2﹣2﹣=,
∵∠ECB′=45°,∴△ECB′为等腰直角三角形,∴CE=CB′=×=2.
故答案为2.
14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数= 度.
考点: 线段垂直平分线的性质;菱形的性质.
分析: 此题主要考查线段的垂直平分线的性质和菱形的性质.
根据菱形的性质求出∠ADC=100°,再根据垂直平分线的性质得出AF=DF,从而计算出∠CDF的值.
解答: 解:连接BD,BF
∵∠BAD=80°
∴∠ADC=100°
又∵EF垂直平分AB,AC垂直平分BD
∴AF=BF,BF=DF
∴AF=DF
∴∠FAD=∠FDA=40°
∴∠CDF=100°﹣40°=60°.
故答案为:60.
15、在四边形ABCD中,对角线AC⊥BD且AC=6、BD=8,E、F分别是边AB、CD的中点,则EF= .
分析: 压轴题.本题考查了三角形的中位线平行于第三边并且等于第三边的一半,勾股定理的应用,作辅助线构造出直角三角形是解题的关键.
取BC的中点G,连接EG、FG,根据三角形的中位线平行于第三边并且等于第三边的一半求出EG、FG,并求出EG⊥FG,然后利用勾股定理列式计算即可得解.
解答: 解:如图,取BC的中点G,连接EG、FG,
∵E、F分别是边AB、CD的中点,
∴EG∥AC且EG=AC=×6=3,
FG∥BD且FG=BD=×8=4,
∵AC⊥BD,∴EG⊥FG,∴EF===5.
故答案为:5.
16、已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
【分析】压轴题.本题考查了轴对称﹣最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P的位置.
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
【解答】解:
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形, ∴AC⊥BD,∠QBP=∠MBP, 即Q在AB上,
∵MQ⊥BD, ∴AC∥MQ, ∵M为BC中点, ∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形, ∴BQ∥CD,BQ=CN, ∴四边形BQNC是平行四边形,
∴NQ=BC, ∵四边形ABCD是菱形, ∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5, 即NQ=5, ∴MP+NP=QP+NP=QN=5,
故答案为:5.
17、(2022·江苏·)已知如图,在矩形ABCD中,点E、F分别是AD、BC上一点,将四边形ABFE沿着EF折叠,点B恰好与点D重合,点A与点A'重合,∠A'DC的角平分线交EF于点O,若AE=5,BF=13,则OD=_____.
【答案】
【分析】本题考查了矩形的折叠问题,等边对等角,勾股定理,平行四边形的性质与判定,根据折叠的性质证明四边形是平行四边形是解题的关键.
连接,,根据折叠的性质求得,根据矩形的性质可得,进而可得,,证明,四边形是平行四边形,中勾股定理即可求得的长.
【详解】
如图,连接,
四边形是矩形
,
将四边形ABFE沿着EF折叠,点B恰好与点D重合,点A与点A'重合,
,,
,
在中,,
在与中,,,
是的角平分线,,
又,,
,
又,
四边形是平行四边形,
在中,
,
故答案为:
18、(2022·广东·重庆巴蜀中学九年级开学考试)如图,F为正方形ABCD的边CD上一动点,AB=2,连接BF,过A作AH⊥BF交BC于H,交BF于G,连接CG,当CG为最小值时,CH的长为 _____.
【答案】##
【分析】本题考查正方形的性质,全等三角形的判定和性质,直角三角形斜边中线的性质,等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线.
取AB的中点O,连接OG,OC,根据的长为定值,当O,G,C共线时,CG的值最小,证明CF=CG=BH即可解决问题.
【详解】
解:如图,取AB的中点O,连接OG,OC.
四边形ABCD是正方形,ABC=90°,
AB=2,OB=OA=1,,
AH⊥BF,AGB=90°,
AO=OB,OG=AB=1,
,
当O、G、C共线时,CG的值最小,最小值=,此时如图,
OB=OG=1,OBG=OGB,
ABCD,OBG=CFG,
OGB=CGF,CGF=CFG,CF=CG=,
ABH=BCF=AGB=90°,
∠BAH+∠ABG=90°,∠ABG+∠CBF=90°,∠BAH=∠CBF,
AB=BC,△ABH△BCF (ASA) ,BH=CF=,CH=BC-BH=2-()=3-,
故答案为:
三、解答题
19、如图,△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣4,1),C(﹣1,2).
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,写出B2和C2的坐标;
(3)直接写出△ABC绕原点O顺时针旋转一周扫过的图形面积.
【分析】(1)利用网格特点和旋转的性质画出A、B、C的对应点A1、B1、C1即可;
(2)利用关于原点对称的点的坐标特征写出A2、B2和C2的坐标,然后描点即可;
(3)△ABC绕原点O顺时针旋转一周扫过的图形为圆环,大圆半径为OB,小圆半径为OC,然后利用两圆的面积差求解.
【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,B2(4,﹣1),C2(1,﹣2);
(3)OB==,OC==,
所以△ABC绕原点O顺时针旋转一周扫过的图形面积=π×()2﹣π×()2=12π.
20、如图,点在外,连接,,延长交于,为的中点.
(1)求证:;
(2)若,,,,求的长.
【答案】(1)见解析;(2)
【分析】
(1)连接交于点,根据平行四边形的性质可以判定OF为△DBE的中位线,即可证明;
(2)根据AD=2,∠ACD=90°,∠ADC=60°,可求出AC的长,再根据中位线的性质即可求解;
【解析】
解:(1)连接交于点,
∵四边形是平行四边形,∴,
∵,
∴OF为△DBE的中位线, ∴.
(2)∵AD=2,∠ACD=90°,∠ADC=60°,∴.
∵是的中位线,∴.
∴.
∵,
∴.
21、已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在对角线AC上,且BF=DE,AH=CG,连接FH、HE、BG、FG.
(1)求证:FG=EH.
(2)若EG平分∠AEH,FH平分∠CFG,FG//AB,∠ACD=68°,∠GFH=35°,求∠GHF的度数.
【答案】(1)证明见解析;(2)77°
【分析】
(1)根据平行四边形的性质可得,,通过证明≌即可得证;
(2)利用角平分线的定义可得,再根据平行四边形的性质求出,利用三角形外角的性质即可求解.
【解析】
解:(1)∵四边形ABCD是平行四边形,∴,,∴,
∵,∴,即,
在和中,,∴≌,∴FG=EH;
(2)∵FH平分∠CFG,∠GFH=35°,
∴,
∵FG//AB,
∴,
∵四边形ABCD是平行四边形,
∴,
∴,
∴.
22、已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
考点: 菱形的性质;矩形的判定.
分析: 本题考查了菱形的性质,矩形的判定,平行四边形的判定,主要利用了有一个角是直角的平行四边形是矩形,熟练掌握矩形,菱形与平行四边形的关系是解题的关键.
(1)先判断出四边形AODE是平行四边形,再根据菱形的对角线互相垂直可得AC⊥BD,然后根据有一个角是直角的平行四边形是矩形证明;
(2)根据两直线平行,同旁内角互补求出∠ABC=60°,判断出△ABC是等边三角形,然后根据等边三角形的性质求出OA、OB,然后得到OD,再根据矩形的面积公式列式计算即可得解.
解答: (1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是菱形,
故,四边形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,∴∠ABC=180°﹣120°=60°,
∵AB=BC,∴△ABC是等边三角形,
∴OA=×6=3,OB=×6=3,
∵四边形ABCD是菱形,∴OD=OB=3,
∴四边形AODE的面积=OA OD=3×3=9.
23、阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
图1 图2 图3
解:BC+DE的值为.…………………………(6分)
解决问题:
连接AE,CE,如图.
∵四边形ABCD是平行四边形,∴AB // DC.
∵四边形ABEF是矩形,∴AB // FE,BF=AE.∴DC //FE.
∴四边形DCEF是平行四边形. …………………………(8分)
∴ CE // DF.
∵AC=BF=DF,∴AC=AE=CE.
∴△ACE是等边三角形.…………………………(10分)
∴∠ACE=60°.
∵CE∥DF,∴∠AGF=∠ACE=60°.…………………………(12分)
24、已知:如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别是AB,AC,BC的中点,点H在AB上,且∠EHF=90°,求证:CH⊥AB.
【考点】矩形的判定与性质;直角三角形斜边上的中线.
【专题】证明题.
【分析】本题考查了矩形的判定与性质,利用了矩形的判定与性质,直角三角形的性质,等腰三角形的判定,三角形的内角和定理.
根据矩形的判定与性质,可得OD=OC=OE=OF,根据直角三角形的性质,可得OH=EF=OE=OF,
根据等腰三角形的判定,可得∠CHO=∠OCH,∠OHD=∠ODH,根据三角形的内角和定理,可得答案.
【解答】证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥BC,DF∥CE,∴四边形CEDF是平行四边形.
∵∠ACB=90°,∴四边形CEDF是矩形,∴OD=OC=OE=OF.
在Rt△EHF中,OH=EF=OE=OF,∴OH=CD=OC=OD,
∴在△CHD中,∠CHO=∠OCH,∠OHD=∠ODH.
∵∠CHO+∠OCH+∠OHD+∠ODH=180°,
∴∠CHO+∠OHD=90°,即CH⊥AB.
25、已知:如图①,在矩形ABCD中,AB=5,AD=.过A作AH⊥BD于H.
(1)将△AHB沿AB翻折,得△AEB.求证:∠EAB=∠ADB;
(2)如图②,将△ABE绕点B顺时针旋转,记旋转中的△ABE为△A′BE′,在旋转过程中,延长A′E′与对角线BD交于点Q,与边AD交于点P,问是否存在这样的Q、P两点,使△DQP为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
(1)证明:由翻折可知:∠EAB=∠BAH.…………(1分)
∵∠BAH+∠DAH=∠DAH+∠ADB=90°.
∴∠BAH =∠ADB,…………(2分)
∴∠EAB=∠ADB. ……………………(3分)
(2)如图①所示,当PD=DQ时,
由∠1=∠2可得∠A′BQ=∠ A′QB,∴A′Q= A′B=5,∴E′Q=1.
在Rt△E′BQ中,BQ==.
∴DQ=.……………………(5分)
如图②所示,当PQ=PD,
由∠1=∠2可得∠1=∠4,∴BQ= A′B=5,
∴DQ=BD—BQ=—5=.……………………(7分)
∴综上可知:当DQ=或时,△DPQ是等腰三角形.………(8分)
(
图
①
) (
图
②
)
26、(2020秋 永年区期中)(1)如图1,点、分别在正方形的边、上,,求证:;
(2)如图2,四边形中,,,,点、分别在边、 上,则当与满足什么关系时,仍有,说明理由.
【分析】(1)根据旋转的性质可以得到,则,只要再证明即可;
(2)延长至,使,连接,证,再证,即可得出答案.
【解析】证明:(1)如图1:把绕点逆时针旋转至,
则,
,,,
又,即,
,
在和中,,..
又,,;
(2)当时,仍有,
理由如下:如图2,延长至,使,连接,
,,,
在和中,,,,,
,,,
在和中,,,
,即.
27、如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
分析: 本题是四边形综合题,其中涉及到直角梯形的性质,矩形的判定与性质,等腰直角三角形的性质,轴对称的性质,等腰三角形的性质,正方形的性质等知识,综合性较强,难度适中.运用数形结合、方程思想是解题的关键.
(1)由DM=2t,根据AM=AD﹣DM即可求出AM=8﹣2t;先证明四边形CNPD为矩形,
得出DP=CN=6﹣t,则AP=AD﹣DP=2+t;
(2)根据四边形ANCP为平行四边形时,可得6﹣t=8﹣(6﹣t),解方程即可;
(3))①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,
列出方程6﹣t﹣2t=8﹣(6﹣t),求解即可,
②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正
方形,则CD=AD,由AD=8,可得CD=8,利用勾股定理求得AC即可.
解答: 解:(1)如图1.
∵DM=2t, ∴AM=AD﹣DM=8﹣2t.
∵在直角梯形ABCD中,AD∥BC,∠ADC=90°,NP⊥AD于点P, ∴四边形CNPD为矩形,
∴DP=CN=BC﹣BN=6﹣t, ∴AP=AD﹣DP=8﹣(6﹣t)=2+t;
故答案为:8﹣2t,2+t.
(2)∵四边形ANCP为平行四边形时,CN=AP,
∴6﹣t=8﹣(6﹣t),解得t=2,
(3)①存在时刻t=1,使四边形AQMK为菱形.理由如下:
∵NP⊥AD,QP=PK, ∴当PM=PA时有四边形AQMK为菱形,
∴6﹣t﹣2t=8﹣(6﹣t),解得t=1,
②要使四边形AQMK为正方形.
∵∠ADC=90°, ∴∠CAD=45°. ∴四边形AQMK为正方形,则CD=AD,
∵AD=8, ∴CD=8, ∴AC=8.
故答案为:8.
2021-2022学年苏科版七年级数学下册
一、选择题
1、下列标志既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2、矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B. 对角线相等
C.对角线互相平分 D. 两组对角分别相等
3、如图,菱形ABCD的边长为4,过点A、C作对角线AC的垂线,分别交CB和AD的延长线于点E、F,AE=3,则四边形AECF的周长为( )
A. 22 B. 18 C. 14 D. 11
4、如图,在 ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
5、如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD=( )
A.3 B.4 C.4.8 D.5
6、如图,正方形的面积为256,点F在上,点E在的延长线上,的面积为200,则的长为( )
A.10 B.11 C.12 D.15
7、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A. 2.5 B. C. D. 2
8、如图,在平行四边形中,,是锐角,于点,是的中点,连接;若,则的长为( )
A. B. C. D.
9、(泰州海陵区、医药高新区联考20-21八下期末)如图,边长为定值的正方形ABCD的中心与正方形EFGH的顶点重合,且与边BC、AB相交于M、N,图中阴影部分的面积记为S,两条线段MB、BN的长度之和记为l,将正方形 EFGH绕点E逆时针旋转适当角度,则有( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
10、如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①∠EFH=45°;②△AHD≌△EHF;③∠AEF+∠HAD=45°; ④若=2,则.其中结论正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
11、(南京浦口区第三中学21-22八上12月月考)如图,平行四边形ABCD,AD=5,AB=8,点A的坐标为(-3,0)点C的坐标为______.
12、(2021春 昆明期末)如图,某小区要在一块矩形的空地上建造一个如图所示的四边形花园,点,,,分别为边,,,的中点,若,,则四边形的面积为 .
13、如图,将边长为的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE= .
14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数= 度.
15、在四边形ABCD中,对角线AC⊥BD且AC=6、BD=8,E、F分别是边AB、CD的中点,则EF= .
16、已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
17、(2022·江苏·)已知如图,在矩形ABCD中,点E、F分别是AD、BC上一点,将四边形ABFE沿着EF折叠,点B恰好与点D重合,点A与点A'重合,∠A'DC的角平分线交EF于点O,若AE=5,BF=13,则OD=_____.
18、(2022·广东·重庆巴蜀中学九年级开学考试)如图,F为正方形ABCD的边CD上一动点,AB=2,连接BF,过A作AH⊥BF交BC于H,交BF于G,连接CG,当CG为最小值时,CH的长为 _____.
三、解答题
19、如图,△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣4,1),C(﹣1,2).
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,写出B2和C2的坐标;
(3)直接写出△ABC绕原点O顺时针旋转一周扫过的图形面积.
20、如图,点在外,连接,,延长交于,为的中点.
(1)求证:;
(2)若,,,,求的长.
21、已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在对角线AC上,且BF=DE,AH=CG,连接FH、HE、BG、FG.
(1)求证:FG=EH.
(2)若EG平分∠AEH,FH平分∠CFG,FG//AB,∠ACD=68°,∠GFH=35°,求∠GHF的度数.
22、已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
23、阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
图1 图2 图3
24、已知:如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别是AB,AC,BC的中点,点H在AB上,且∠EHF=90°,求证:CH⊥AB.
25、已知:如图①,在矩形ABCD中,AB=5,AD=.过A作AH⊥BD于H.
(1)将△AHB沿AB翻折,得△AEB.求证:∠EAB=∠ADB;
(2)如图②,将△ABE绕点B顺时针旋转,记旋转中的△ABE为△A′BE′,在旋转过程中,延长A′E′与对角线BD交于点Q,与边AD交于点P,问是否存在这样的Q、P两点,使△DQP为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
26、(2020秋 永年区期中)(1)如图1,点、分别在正方形的边、上,,求证:;
(2)如图2,四边形中,,,,点、分别在边、 上,则当与满足什么关系时,仍有,说明理由.
27、如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
第9章 中心对称图形—平行四边形 单元综合练习题(培优)
2021-2022学年苏科版七年级数学下册(解析)
一、选择题
1、下列标志既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
分析: 掌握中心对称图形与轴对称图形的概念,要注意:轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
根据轴对称图形与中心对称图形的概念求解.
解答: 解:A、是轴对称图形,也是中心对称图形,故A选项符合题意;
B、是轴对称图形,不是中心对称图形,故B选项不符合题意;
C、不是轴对称图形,是中心对称图形,故C选项不符合题意;
D、是轴对称图形,不是中心对称图形,故D选项不符合题意.
故选A.
2、矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B. 对角线相等
C.对角线互相平分 D. 两组对角分别相等
分析: 根据矩形与菱形的性质对各选项分析判断后利用排除法求解.
解答: 解:A、矩形与菱形的两组对边都分别平行,故本选项错误;
B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;
C、矩形与菱形的对角线都互相平分,故本选项错误;
D、矩形与菱形的两组对角都分别相等,故本选项错误.
故选B.
3、如图,菱形ABCD的边长为4,过点A、C作对角线AC的垂线,分别交CB和AD的延长线于点E、F,AE=3,则四边形AECF的周长为( )
A. 22 B. 18 C. 14 D. 11
分析:本题考查了菱形的对角线平分一组对角的性质,等角的余角相等的性质,平行四边形的判定与性质,熟记性质并求出EC的长度是解题的关键.
根据菱形的对角线平分一组对角可得∠BAC=∠BCA,再根据等角的余角相等求出∠BAE=∠E,根据等角对等边可得BE=AB,然后求出EC,同理可得AF,然后判断出四边形AECF是平行四边形,再根据周长的定义列式计算即可得解.
解答: 解:在菱形ABCD中,∠BAC=∠BCA,
∵AE⊥AC,
∴∠BAC+∠BAE=∠BCA+∠E=90°,
∴∠BAE=∠E,
∴BE=AB=4,
∴EC=BE+BC=4+4=8,
同理可得AF=8,
∵AD∥BC,
∴四边形AECF是平行四边形,
∴四边形AECF的周长=2(AE+EC)=2(3+8)=22.
故选:A.
4、如图,在 ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
【答案】C
【分析】此题主要考查了平行四边形的性质和角平分线的性质,勾股定理的逆定理,勾股定理,关键是掌握平行四边形对边平行且相等.
根据平行四边形的性质和角平分线的定义可得AD=BC=EB=5,根据勾股定理的逆定理可得∠AED=90°,再根据平行四边形的性质可得CD=AB=8,∠EDC=90°,根据勾股定理可求CE的长.
【解析】
解:∵CE平分∠BCD,∴∠BCE=∠DCE,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠BEC=∠DCE,∴∠BEC=∠BCE,
∴BC=BE=5,∴AD=5,
∵EA=3,ED=4,
在△AED中,32+42=52,即EA2+ED2=AD2,
∴∠AED=90°,
∴CD=AB=3+5=8,∠EDC=90°,
在Rt△EDC中,CE===4.
故选:C.
5、如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD=( )
A.3 B.4 C.4.8 D.5
【答案】D
【分析】
由勾股定理逆定理易证为直角三角形.又由DE垂直平分AC,易证∠AED=90°,AE=CE=4,即可推出DE是△ABC的中位线,即求出DE=BC=3,最后在中,利用勾股定理即可求出CD的长.
【解析】
∵AB=10,BC=6,AC=8,∴,∴∠ACB=90°,
∵DE垂直平分AC,
∴∠AED=90°,AE=CE=4,∴DE∥BC,
∴DE是△ABC的中位线,∴DE=BC=3.
在中,.
6、如图,正方形的面积为256,点F在上,点E在的延长线上,的面积为200,则的长为( )
A.10 B.11 C.12 D.15
【答案】C
【分析】本题考查了正方形,等腰直角三角形面积的计算,考查了直角三角形中勾股定理的运用,本题中求证CF=CE是解题的关键.
先证明Rt△CDF≌Rt△CBE,故CE=CF,根据△CEF的面积计算CE,根据正方形ABCD的面积计算BC,根据勾股定理计算BE.
【详解】
解:∵∠ECF=90°,∠DCB=90°,
∴∠BCE=∠DCF,∴,∴△CDF≌△CBE,故CF=CE.
因为Rt△CEF的面积是200,即 CE CF=200,故CE=20,
正方形ABCD的面积=BC2=256,得BC=16.根据勾股定理得:BE==12.
故选:C.
7、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A. 2.5 B. C. D. 2
分析: 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,正方形的性质,勾股定理,熟记各性质并作辅助线构造出直角三角形是解题的关键.
连接AC、CF,根据正方形性质求出AC、CF,∠ACD=∠GCF=45°,再求出∠ACF=90°,然后利用勾股定理列式求出AF,再根据直角三角形斜边上的中线等于斜边的一半解答即可.
解答: 解:如图,连接AC、CF,
∵正方形ABCD和正方形CEFG中,BC=1,CE=3,
∴AC=,CF=3,
∠ACD=∠GCF=45°,
∴∠ACF=90°,
由勾股定理得,AF===2,
∵H是AF的中点,
∴CH=AF=×2=.
故选:B.
8、如图,在平行四边形中,,是锐角,于点,是的中点,连接;若,则的长为( )
A. B. C. D.
【答案】B
【分析】
延长EF,DA交于G,连接DE,先证明△AFG≌△BFE,进而得到BE=AG,F是GE的中点,结合条件BF⊥GE进而得到BF是线段GE的垂直平分线,得到GD=DE,最后在Rt△AED中使用勾股定理即可求解.
【解析】
解:延长EF,DA交于G,连接DE,如下图所示:
∵F是AB的中点,∴AF=BF,
∵四边形ABCD是平行四边形,
∴AB∥BC,∴∠GAB=∠EBF
且∠GFA=∠EFB,∴△AFG≌△BFE(ASA),
设,
由GF=EF,且∠DFE=90°知,
DF是线段GE的垂直平分线,
∴,
在Rt△BAE中,.
在Rt△AED中,,
∴,解得,
∴,
故选:B.
9、(泰州海陵区、医药高新区联考20-21八下期末)如图,边长为定值的正方形ABCD的中心与正方形EFGH的顶点重合,且与边BC、AB相交于M、N,图中阴影部分的面积记为S,两条线段MB、BN的长度之和记为l,将正方形 EFGH绕点E逆时针旋转适当角度,则有( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
【答案】D
【解析】
【分析】本题考了全等三角形的判定和性质,正确寻找全等三角形是解题的关键.
如图,连接,,可证明,可得 ,根据,是一个定值,,也是一个定值,可得结论.
【详解】
解:如图,连接,.
∵边长为定值的正方形ABCD的中心与正方形EFGH的顶点重合,
即点E是正方形ABCD的中心,
∴,,
又∵,∴,∴
在和中,,∴,∴,
∴,是一个定值,,也是一个定值,即:与均不变,
故选:.
10、如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①∠EFH=45°;②△AHD≌△EHF;③∠AEF+∠HAD=45°; ④若=2,则.其中结论正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
【答案】A
【分析】①根据正方形的性质证明∠ADB=45°,进而得△DFG为等腰直角三角形,根据等腰三角形的三线合一性质得∠EFH=∠EFD=45°,故①正确;
②根据矩形性质得AF=EB,∠BEF=90°,再证明△AFH≌△EGH得EH=AH,进而证明△EHF≌△AHD,故②正确;
③由△EHF≌△AHD得∠EHF=∠AHD,怀AH=EH得∠AEF+∠HEF=45°,进而得∠AEF+∠HAD=45°,故③正确;
④如图,过点H作MN⊥AD于点M,与BC交于点N,设EC=FD=FG=x,则BE=AF=EG=2x,BC=DC=AB=AD=3x,HM=x,AM=x,HN=x,由勾股定理得AH2,再由三角形的面积公式得,便可判断④的正误,
【解答】证明:①在正方形ABCD中,∠ADC=∠C=90°,∠ADB=45°,
∵EF∥CD,∴∠EFD=90°,∴四边形EFDC是矩形.
在Rt△FDG中,∠FDG=45°,∴FD=FG,
∵H是DG中点,∴∠EFH=∠EFD=45°故①正确;
②∵四边形ABEF是矩形,∴AF=EB,∠BEF=90°,
∵BD平分∠ABC,∴∠EBG=∠EGB=45°,∴BE=GE,∴AF=EG.
在Rt△FGD中,H是DG的中点,∴FH=GH,FH⊥BD,
∵∠AFH=∠AFE+∠GFH=90°+45°=135°,
∠EGH=180°﹣∠EGB=180°﹣45°=135°,
∴∠AFH=∠EGH,∴△AFH≌△EGH(SAS),∴EH=AH,
∵EF=AD,FH=DH,∴△EHF≌△AHD(SSS),故②正确;
③∵△EHF≌△AHD,∴∠EHF=∠AHD,∴∠AHE=∠DHF=90°,
∵AH=EH,∴∠AEH=45°,即∠AEF+∠HEF=45°,
∵∠HEF=∠HAD,∴∠AEF+∠HAD=45°,故③正确;
④如图,过点H作MN⊥AD于点M,与BC交于点N,
设EC=FD=FG=x,则BE=AF=EG=2x,
∴BC=DC=AB=AD=3x,HM=x,AM=x,HN=x,
∴AH2=,∴=,故④错误;
故选:A.
二、填空题
11、(南京浦口区第三中学21-22八上12月月考)如图,平行四边形ABCD,AD=5,AB=8,点A的坐标为(-3,0)点C的坐标为______.
【答案】(8,4)
【分析】本题考查平行四边形性质,勾股定理,平行x轴两点坐标特征,解答本题的关键是熟练掌握平行于x轴的直线上的点的纵坐标相同,平行于y轴的直线上的点的横坐标相同.
先根据勾股定理得到OD的长,即可得到点D的坐标,再根据平行四边形的性质和平行x轴两点坐标特征即可得到点C的坐标.
【详解】
解:∵点A的坐标为(-3,0),
在Rt△ADO中,AD=5, AO=3,,∴OD==,∴D(0,4),
∵平行四边形ABCD,∴AB=CD=8,AB∥CD,
∵AB在x轴上,∴CD∥x轴,
∴C、D两点的纵坐标相同,∴C(8,4) .
故答案为(8,4).
12、(2021春 昆明期末)如图,某小区要在一块矩形的空地上建造一个如图所示的四边形花园,点,,,分别为边,,,的中点,若,,则四边形的面积为 .
【分析】根据矩形的性质推出,得到平行四边形,推出,,同理得到,,推出,根据三角形的面积公式求出即可.
【解析】连接、,
四边形是矩形,,,
、分别为边、的中点,,
四边形是平行四边形,,,
同理,,
,,
四边形的面积是.
故答案为:100.
13、如图,将边长为的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE= .
【分析】计算题.本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.
根据正方形的性质得AC=(2+)=2+2,∠ACD=∠BAC=45°,再利用旋转的性质得∠BAB′=45°,AB′=AB=2+,∠AB′C′=∠B=90°,于是可判断点B′在AC上,所以CB′=AC﹣AB′=,然后利用△ECB′为等腰直角三角形易得CE=CB′=2.
【解答】解:∵四边形ABCD为正方形,
∴AC=(2+)=2+2,∠ACD=∠BAC=45°,
∵正方形ABCD绕点A逆时针方向旋转45°至正方形AB′C′D′,
∴∠BAB′=45°,AB′=AB=2+,∠AB′C′=∠B=90°,
∴点B′在AC上,∴CB′=AC﹣AB′=2+2﹣2﹣=,
∵∠ECB′=45°,∴△ECB′为等腰直角三角形,∴CE=CB′=×=2.
故答案为2.
14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数= 度.
考点: 线段垂直平分线的性质;菱形的性质.
分析: 此题主要考查线段的垂直平分线的性质和菱形的性质.
根据菱形的性质求出∠ADC=100°,再根据垂直平分线的性质得出AF=DF,从而计算出∠CDF的值.
解答: 解:连接BD,BF
∵∠BAD=80°
∴∠ADC=100°
又∵EF垂直平分AB,AC垂直平分BD
∴AF=BF,BF=DF
∴AF=DF
∴∠FAD=∠FDA=40°
∴∠CDF=100°﹣40°=60°.
故答案为:60.
15、在四边形ABCD中,对角线AC⊥BD且AC=6、BD=8,E、F分别是边AB、CD的中点,则EF= .
分析: 压轴题.本题考查了三角形的中位线平行于第三边并且等于第三边的一半,勾股定理的应用,作辅助线构造出直角三角形是解题的关键.
取BC的中点G,连接EG、FG,根据三角形的中位线平行于第三边并且等于第三边的一半求出EG、FG,并求出EG⊥FG,然后利用勾股定理列式计算即可得解.
解答: 解:如图,取BC的中点G,连接EG、FG,
∵E、F分别是边AB、CD的中点,
∴EG∥AC且EG=AC=×6=3,
FG∥BD且FG=BD=×8=4,
∵AC⊥BD,∴EG⊥FG,∴EF===5.
故答案为:5.
16、已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
【分析】压轴题.本题考查了轴对称﹣最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P的位置.
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
【解答】解:
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形, ∴AC⊥BD,∠QBP=∠MBP, 即Q在AB上,
∵MQ⊥BD, ∴AC∥MQ, ∵M为BC中点, ∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形, ∴BQ∥CD,BQ=CN, ∴四边形BQNC是平行四边形,
∴NQ=BC, ∵四边形ABCD是菱形, ∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5, 即NQ=5, ∴MP+NP=QP+NP=QN=5,
故答案为:5.
17、(2022·江苏·)已知如图,在矩形ABCD中,点E、F分别是AD、BC上一点,将四边形ABFE沿着EF折叠,点B恰好与点D重合,点A与点A'重合,∠A'DC的角平分线交EF于点O,若AE=5,BF=13,则OD=_____.
【答案】
【分析】本题考查了矩形的折叠问题,等边对等角,勾股定理,平行四边形的性质与判定,根据折叠的性质证明四边形是平行四边形是解题的关键.
连接,,根据折叠的性质求得,根据矩形的性质可得,进而可得,,证明,四边形是平行四边形,中勾股定理即可求得的长.
【详解】
如图,连接,
四边形是矩形
,
将四边形ABFE沿着EF折叠,点B恰好与点D重合,点A与点A'重合,
,,
,
在中,,
在与中,,,
是的角平分线,,
又,,
,
又,
四边形是平行四边形,
在中,
,
故答案为:
18、(2022·广东·重庆巴蜀中学九年级开学考试)如图,F为正方形ABCD的边CD上一动点,AB=2,连接BF,过A作AH⊥BF交BC于H,交BF于G,连接CG,当CG为最小值时,CH的长为 _____.
【答案】##
【分析】本题考查正方形的性质,全等三角形的判定和性质,直角三角形斜边中线的性质,等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线.
取AB的中点O,连接OG,OC,根据的长为定值,当O,G,C共线时,CG的值最小,证明CF=CG=BH即可解决问题.
【详解】
解:如图,取AB的中点O,连接OG,OC.
四边形ABCD是正方形,ABC=90°,
AB=2,OB=OA=1,,
AH⊥BF,AGB=90°,
AO=OB,OG=AB=1,
,
当O、G、C共线时,CG的值最小,最小值=,此时如图,
OB=OG=1,OBG=OGB,
ABCD,OBG=CFG,
OGB=CGF,CGF=CFG,CF=CG=,
ABH=BCF=AGB=90°,
∠BAH+∠ABG=90°,∠ABG+∠CBF=90°,∠BAH=∠CBF,
AB=BC,△ABH△BCF (ASA) ,BH=CF=,CH=BC-BH=2-()=3-,
故答案为:
三、解答题
19、如图,△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣4,1),C(﹣1,2).
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,写出B2和C2的坐标;
(3)直接写出△ABC绕原点O顺时针旋转一周扫过的图形面积.
【分析】(1)利用网格特点和旋转的性质画出A、B、C的对应点A1、B1、C1即可;
(2)利用关于原点对称的点的坐标特征写出A2、B2和C2的坐标,然后描点即可;
(3)△ABC绕原点O顺时针旋转一周扫过的图形为圆环,大圆半径为OB,小圆半径为OC,然后利用两圆的面积差求解.
【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,B2(4,﹣1),C2(1,﹣2);
(3)OB==,OC==,
所以△ABC绕原点O顺时针旋转一周扫过的图形面积=π×()2﹣π×()2=12π.
20、如图,点在外,连接,,延长交于,为的中点.
(1)求证:;
(2)若,,,,求的长.
【答案】(1)见解析;(2)
【分析】
(1)连接交于点,根据平行四边形的性质可以判定OF为△DBE的中位线,即可证明;
(2)根据AD=2,∠ACD=90°,∠ADC=60°,可求出AC的长,再根据中位线的性质即可求解;
【解析】
解:(1)连接交于点,
∵四边形是平行四边形,∴,
∵,
∴OF为△DBE的中位线, ∴.
(2)∵AD=2,∠ACD=90°,∠ADC=60°,∴.
∵是的中位线,∴.
∴.
∵,
∴.
21、已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在对角线AC上,且BF=DE,AH=CG,连接FH、HE、BG、FG.
(1)求证:FG=EH.
(2)若EG平分∠AEH,FH平分∠CFG,FG//AB,∠ACD=68°,∠GFH=35°,求∠GHF的度数.
【答案】(1)证明见解析;(2)77°
【分析】
(1)根据平行四边形的性质可得,,通过证明≌即可得证;
(2)利用角平分线的定义可得,再根据平行四边形的性质求出,利用三角形外角的性质即可求解.
【解析】
解:(1)∵四边形ABCD是平行四边形,∴,,∴,
∵,∴,即,
在和中,,∴≌,∴FG=EH;
(2)∵FH平分∠CFG,∠GFH=35°,
∴,
∵FG//AB,
∴,
∵四边形ABCD是平行四边形,
∴,
∴,
∴.
22、已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
考点: 菱形的性质;矩形的判定.
分析: 本题考查了菱形的性质,矩形的判定,平行四边形的判定,主要利用了有一个角是直角的平行四边形是矩形,熟练掌握矩形,菱形与平行四边形的关系是解题的关键.
(1)先判断出四边形AODE是平行四边形,再根据菱形的对角线互相垂直可得AC⊥BD,然后根据有一个角是直角的平行四边形是矩形证明;
(2)根据两直线平行,同旁内角互补求出∠ABC=60°,判断出△ABC是等边三角形,然后根据等边三角形的性质求出OA、OB,然后得到OD,再根据矩形的面积公式列式计算即可得解.
解答: (1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是菱形,
故,四边形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,∴∠ABC=180°﹣120°=60°,
∵AB=BC,∴△ABC是等边三角形,
∴OA=×6=3,OB=×6=3,
∵四边形ABCD是菱形,∴OD=OB=3,
∴四边形AODE的面积=OA OD=3×3=9.
23、阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
图1 图2 图3
解:BC+DE的值为.…………………………(6分)
解决问题:
连接AE,CE,如图.
∵四边形ABCD是平行四边形,∴AB // DC.
∵四边形ABEF是矩形,∴AB // FE,BF=AE.∴DC //FE.
∴四边形DCEF是平行四边形. …………………………(8分)
∴ CE // DF.
∵AC=BF=DF,∴AC=AE=CE.
∴△ACE是等边三角形.…………………………(10分)
∴∠ACE=60°.
∵CE∥DF,∴∠AGF=∠ACE=60°.…………………………(12分)
24、已知:如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别是AB,AC,BC的中点,点H在AB上,且∠EHF=90°,求证:CH⊥AB.
【考点】矩形的判定与性质;直角三角形斜边上的中线.
【专题】证明题.
【分析】本题考查了矩形的判定与性质,利用了矩形的判定与性质,直角三角形的性质,等腰三角形的判定,三角形的内角和定理.
根据矩形的判定与性质,可得OD=OC=OE=OF,根据直角三角形的性质,可得OH=EF=OE=OF,
根据等腰三角形的判定,可得∠CHO=∠OCH,∠OHD=∠ODH,根据三角形的内角和定理,可得答案.
【解答】证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥BC,DF∥CE,∴四边形CEDF是平行四边形.
∵∠ACB=90°,∴四边形CEDF是矩形,∴OD=OC=OE=OF.
在Rt△EHF中,OH=EF=OE=OF,∴OH=CD=OC=OD,
∴在△CHD中,∠CHO=∠OCH,∠OHD=∠ODH.
∵∠CHO+∠OCH+∠OHD+∠ODH=180°,
∴∠CHO+∠OHD=90°,即CH⊥AB.
25、已知:如图①,在矩形ABCD中,AB=5,AD=.过A作AH⊥BD于H.
(1)将△AHB沿AB翻折,得△AEB.求证:∠EAB=∠ADB;
(2)如图②,将△ABE绕点B顺时针旋转,记旋转中的△ABE为△A′BE′,在旋转过程中,延长A′E′与对角线BD交于点Q,与边AD交于点P,问是否存在这样的Q、P两点,使△DQP为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
(1)证明:由翻折可知:∠EAB=∠BAH.…………(1分)
∵∠BAH+∠DAH=∠DAH+∠ADB=90°.
∴∠BAH =∠ADB,…………(2分)
∴∠EAB=∠ADB. ……………………(3分)
(2)如图①所示,当PD=DQ时,
由∠1=∠2可得∠A′BQ=∠ A′QB,∴A′Q= A′B=5,∴E′Q=1.
在Rt△E′BQ中,BQ==.
∴DQ=.……………………(5分)
如图②所示,当PQ=PD,
由∠1=∠2可得∠1=∠4,∴BQ= A′B=5,
∴DQ=BD—BQ=—5=.……………………(7分)
∴综上可知:当DQ=或时,△DPQ是等腰三角形.………(8分)
(
图
①
) (
图
②
)
26、(2020秋 永年区期中)(1)如图1,点、分别在正方形的边、上,,求证:;
(2)如图2,四边形中,,,,点、分别在边、 上,则当与满足什么关系时,仍有,说明理由.
【分析】(1)根据旋转的性质可以得到,则,只要再证明即可;
(2)延长至,使,连接,证,再证,即可得出答案.
【解析】证明:(1)如图1:把绕点逆时针旋转至,
则,
,,,
又,即,
,
在和中,,..
又,,;
(2)当时,仍有,
理由如下:如图2,延长至,使,连接,
,,,
在和中,,,,,
,,,
在和中,,,
,即.
27、如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
分析: 本题是四边形综合题,其中涉及到直角梯形的性质,矩形的判定与性质,等腰直角三角形的性质,轴对称的性质,等腰三角形的性质,正方形的性质等知识,综合性较强,难度适中.运用数形结合、方程思想是解题的关键.
(1)由DM=2t,根据AM=AD﹣DM即可求出AM=8﹣2t;先证明四边形CNPD为矩形,
得出DP=CN=6﹣t,则AP=AD﹣DP=2+t;
(2)根据四边形ANCP为平行四边形时,可得6﹣t=8﹣(6﹣t),解方程即可;
(3))①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,
列出方程6﹣t﹣2t=8﹣(6﹣t),求解即可,
②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正
方形,则CD=AD,由AD=8,可得CD=8,利用勾股定理求得AC即可.
解答: 解:(1)如图1.
∵DM=2t, ∴AM=AD﹣DM=8﹣2t.
∵在直角梯形ABCD中,AD∥BC,∠ADC=90°,NP⊥AD于点P, ∴四边形CNPD为矩形,
∴DP=CN=BC﹣BN=6﹣t, ∴AP=AD﹣DP=8﹣(6﹣t)=2+t;
故答案为:8﹣2t,2+t.
(2)∵四边形ANCP为平行四边形时,CN=AP,
∴6﹣t=8﹣(6﹣t),解得t=2,
(3)①存在时刻t=1,使四边形AQMK为菱形.理由如下:
∵NP⊥AD,QP=PK, ∴当PM=PA时有四边形AQMK为菱形,
∴6﹣t﹣2t=8﹣(6﹣t),解得t=1,
②要使四边形AQMK为正方形.
∵∠ADC=90°, ∴∠CAD=45°. ∴四边形AQMK为正方形,则CD=AD,
∵AD=8, ∴CD=8, ∴AC=8.
故答案为:8.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
