2021-2022学年苏科版数学八年级下册9.1图形的旋转课后补充习题分层练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级下册9.1图形的旋转课后补充习题分层练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 612.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 14:57:30 | ||
图片预览

文档简介
9.1图形的旋转-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)
【A夯实基础】
A1、(1) 在平面内,将图形绕_______沿某个方向转动_________,这样的图形运动称为旋转。
(2)钟表上的指针随时间的变化而移动,这可以看作是数学上的__________。
(3)图形的旋转只改变图形的_________,而不改变图形的_______________。
(4)经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了_______的角度,任意一对对应点与旋转中心的连线所成的角都________,对应点到旋转中心的距离_________。
(5)△ABC绕一点旋转到△A' B' C',则△ABC和△A' B' C'的关系是__________。
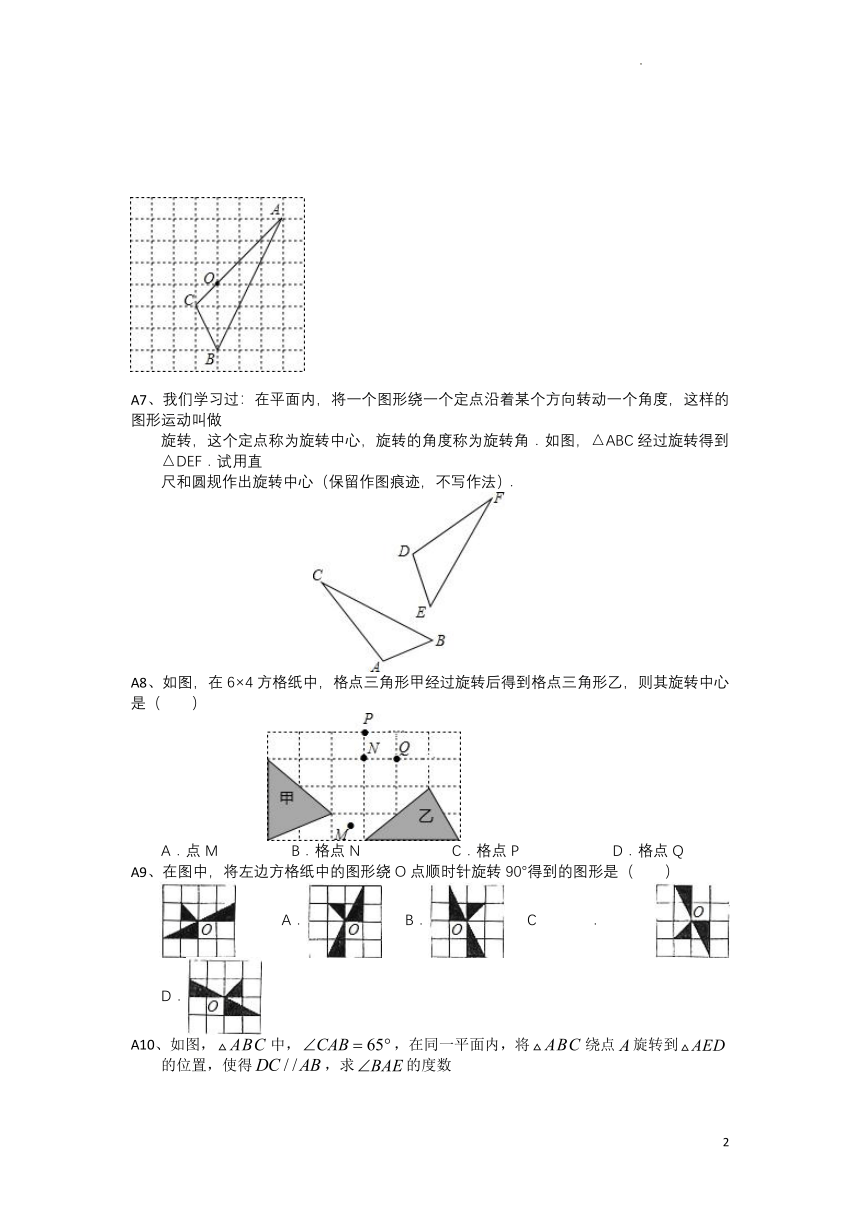
A2、如图,ΔABP是由ΔACD按顺时针方向旋转某一角度得到的,若∠BAP=60°,则在这一旋转过程中,旋转中心是____________,旋转角度为____________.
A3、如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度到ABC的位置,使得点A,B,C在同一条直线上,那么这个角度等于( )
A .120° B .90° C .60° D .30°
A4、如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,
则旋转的角度为( )
A.30° B.45° C.90° D.135°
A5、分析图①、②、④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.
A6、画△ABC绕O点顺时针方向旋转90°后得到△A′B′C′.
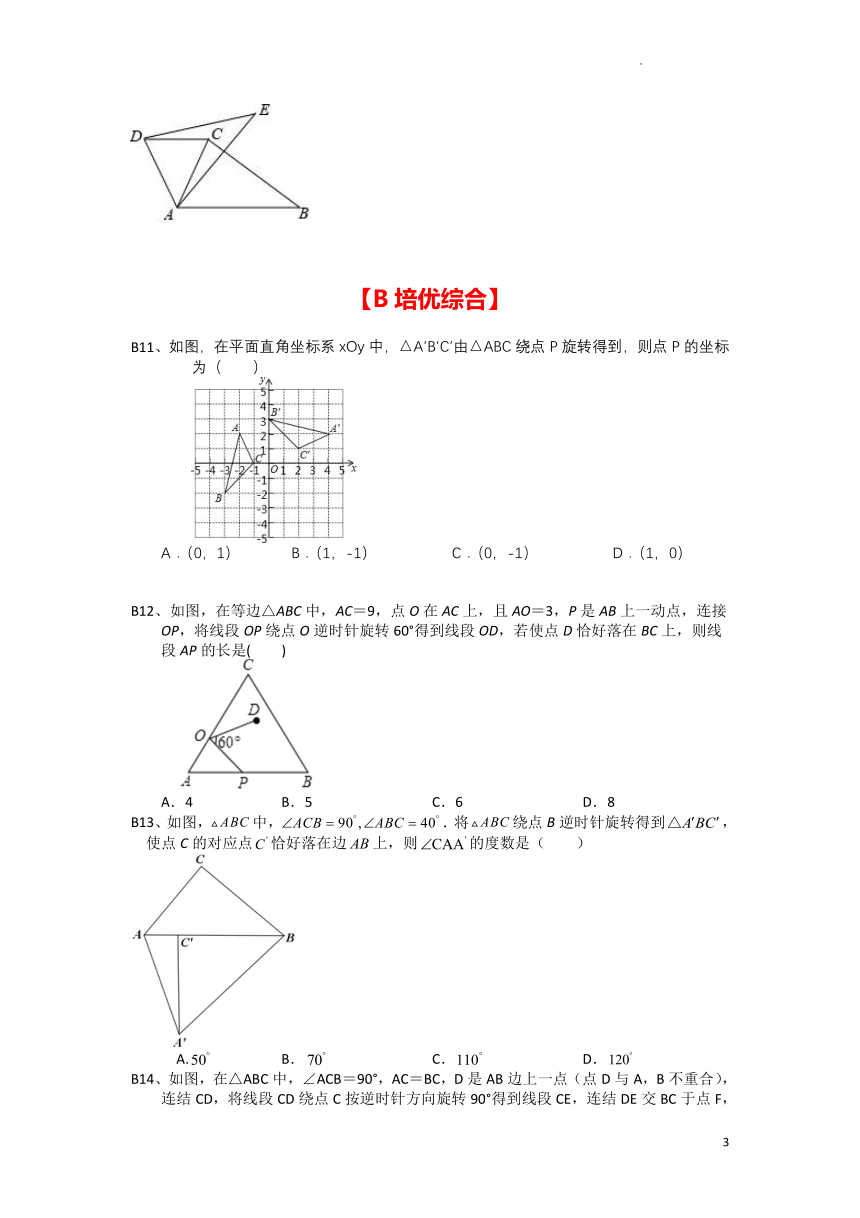
A7、我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做
旋转,这个定点称为旋转中心,旋转的角度称为旋转角.如图,△ABC经过旋转得到△DEF.试用直
尺和圆规作出旋转中心(保留作图痕迹,不写作法).
A8、如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.点M B.格点N C.格点P D.格点Q
A9、在图中,将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是( )
A. B. C. D.
A10、如图,中,,在同一平面内,将绕点旋转到的位置,使得,求的度数
【B培优综合】
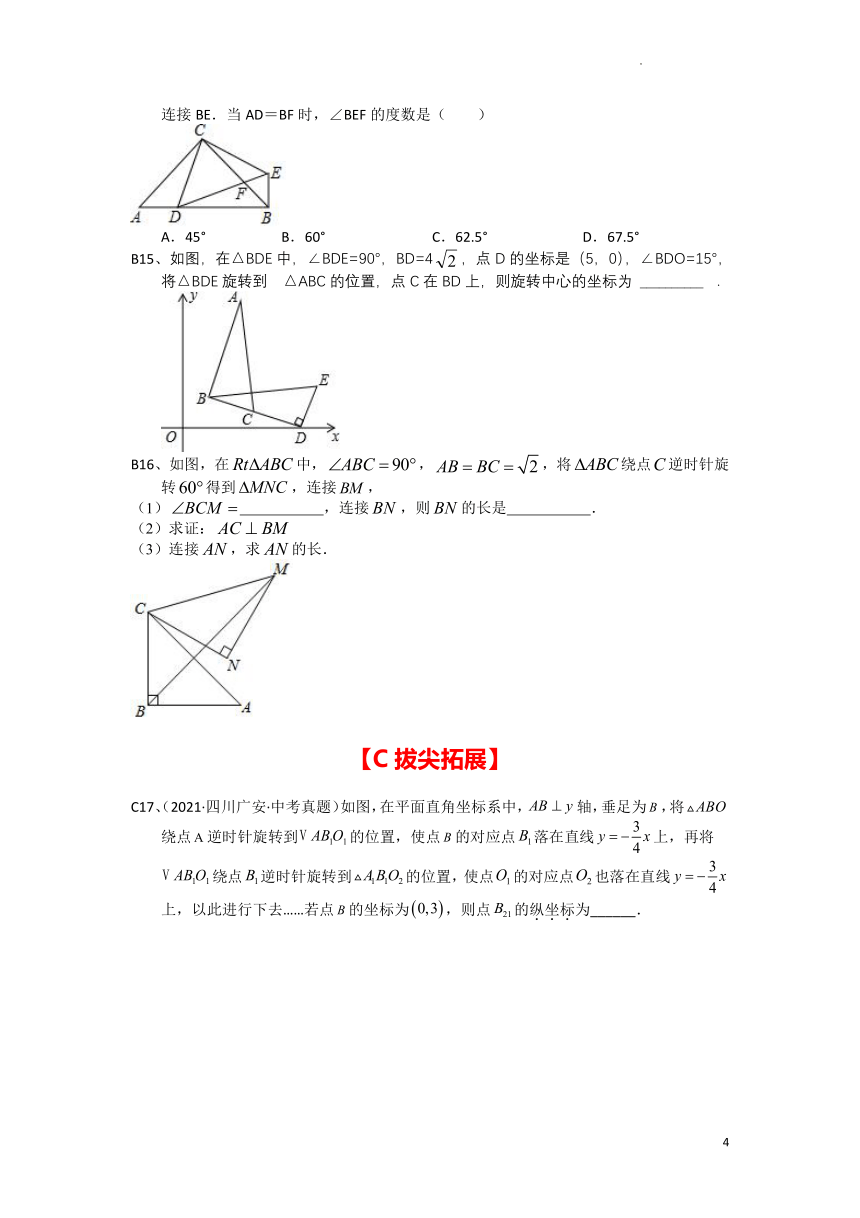
B11、如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
A.(0,1) B.(1,-1) C.(0,-1) D.(1,0)
B12、如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,若使点D恰好落在BC上,则线段AP的长是( )
A.4 B.5 C.6 D.8
B13、如图,中,.将绕点B逆时针旋转得到,使点C的对应点恰好落在边上,则的度数是( )
A. B. C. D.
B14、如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.当AD=BF时,∠BEF的度数是( )
A.45° B.60° C.62.5° D.67.5°
B15、如图,在△BDE中,∠BDE=90°,BD=4,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转到 △ABC的位置,点C在BD上,则旋转中心的坐标为 __________ .
B16、如图,在中,,,将绕点逆时针旋转得到,连接,
(1) ,连接,则的长是 .
(2)求证:
(3)连接,求的长.
【C拔尖拓展】
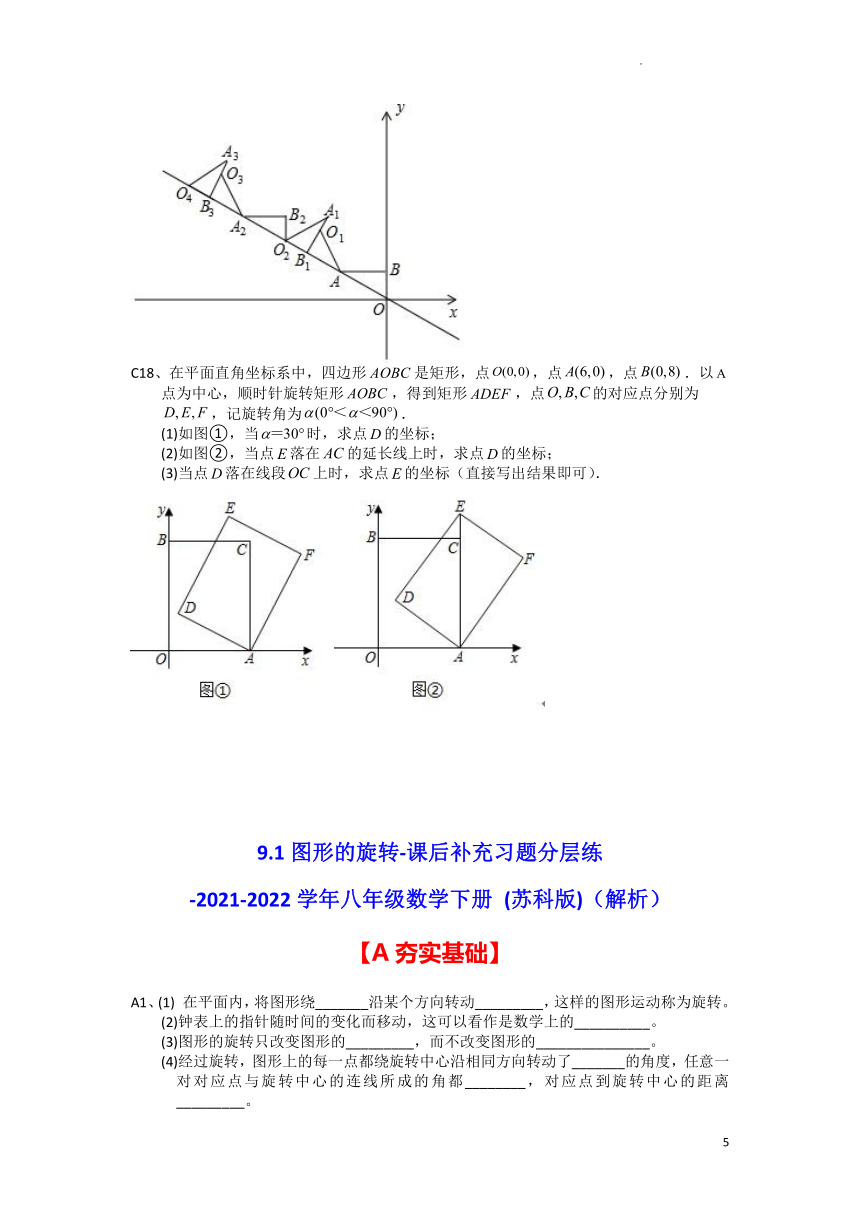
C17、(2021·四川广安·中考真题)如图,在平面直角坐标系中,轴,垂足为,将绕点逆时针旋转到的位置,使点的对应点落在直线上,再将绕点逆时针旋转到的位置,使点的对应点也落在直线上,以此进行下去……若点的坐标为,则点的纵坐标为______.
C18、在平面直角坐标系中,四边形是矩形,点,点,点.以点为中心,顺时针旋转矩形,得到矩形,点的对应点分别为,记旋转角为.
(1)如图①,当时,求点的坐标;
(2)如图②,当点落在的延长线上时,求点的坐标;
(3)当点落在线段上时,求点的坐标(直接写出结果即可).
9.1图形的旋转-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、(1) 在平面内,将图形绕_______沿某个方向转动_________,这样的图形运动称为旋转。
(2)钟表上的指针随时间的变化而移动,这可以看作是数学上的__________。
(3)图形的旋转只改变图形的_________,而不改变图形的_______________。
(4)经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了_______的角度,任意一对对应点与旋转中心的连线所成的角都________,对应点到旋转中心的距离_________。
(5)△ABC绕一点旋转到△A' B' C',则△ABC和△A' B' C'的关系是__________。
答案:(1)某个点;某个角度 (2)旋转 (3)位置;大小,形状
(4)相同;相等;相等 (5)全等
A2、如图,ΔABP是由ΔACD按顺时针方向旋转某一角度得到的,若∠BAP=60°,则在这一旋转过程中,旋转中心是____________,旋转角度为____________.
【分析】本题考查旋转的性质,明确旋转前后的图形大小和形状不变,正确确定对应角,对应边是解答此题的关键.
根据条件得出AD=AP,AC=AB,确定旋转中心,根据条件得出∠DAP=∠CAB=90°,确定旋转角度数.
【详解】
解:∵△ABP是由△ACD按顺时针方向旋转而得,
∴△ABP≌△ACD,
∴∠DAC=∠PAB=60°,AD=AP,AC=AB,
∴∠DAP=∠CAB=90°,
∴△ABP是△ACD以点A为旋转中心顺时针旋转90°得到的.
故答案为:A,90°
A3、如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度到ABC的位置,使得点A,B,C在同一条直线上,那么这个角度等于( )
A .120° B .90° C .60° D .30°
试题分析:利用旋转的性质计算.
解:∵∠ABC=60°,
∴旋转角∠CB=180°-60°=120°.
∴这个旋转角度等于120°.
故选:A.
A4、如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,
则旋转的角度为( )
A.30° B.45° C.90° D.135°
答案:C
试题分析:根据旋转的性质,对应边的夹角∠BOD即为旋转角.
∵△AOB绕点O按逆时针方向旋转到△COD的位置,
∴对应边OB、OD的夹角∠BOD即为旋转角,
∴旋转的角度为90°.
故选C.
A5、分析图①、②、④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.
分析:由①到②是旋转了90°,由②到④是旋转了180度,即通过两次旋转90度得到,据此即可判断.
解析:如图
A6、画△ABC绕O点顺时针方向旋转90°后得到△A′B′C′.
分析:根据旋转的性质,将A,B,C绕O点顺时针旋转90°,由此即可画出旋转后的图形.
解析:如图所示:
A7、我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做
旋转,这个定点称为旋转中心,旋转的角度称为旋转角.如图,△ABC经过旋转得到△DEF.试用直
尺和圆规作出旋转中心(保留作图痕迹,不写作法).
分析:根据旋转的性质,连接对应点AD、BE,再分别作AD、BE的垂直平分线,相交于点O,
则点O即为旋转中心.
解析:如图所示,点O即为△ABC旋转到△DEF的旋转中心.
A8、如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.点M B.格点N C.格点P D.格点Q
答案:B
试题分析:此题可根据旋转前后对应点到旋转中心的距离相等来判断所求的旋转中心.
试题解析:如图,连接N和两个三角形的对应点;
发现两个三角形的对应点到点N的距离相等,因此格点N就是所求的旋转中心;
故选B.
A9、在图中,将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是( )
A. B. C. D.
答案:B
分析:根据旋转的性质,找出图中三角形的关键处(旋转中心)按顺时针方向旋转90°后的形状即可选择答案.
解析:根据旋转的性质可知,绕O点顺时针旋转90°得到的图形是.
故选B.
A10、如图,中,,在同一平面内,将绕点旋转到的位置,使得,求的度数
【答案】∠BAE=50°
【分析】本题考查的是旋转变换,掌握平行线的性质、旋转变换的性质是解题的关键.
根据平行线的性质得到∠ACD=∠CAB=65°,根据旋转变换的性质计算即可.
【详解】
解:∵DC∥AB,∴∠ACD=∠CAB=65°,
由旋转的性质可知,AD=AC,∠DAE=∠CAB=65°,∴∠ADC=∠CAB=65°,
∴∠CAD=180°-∠ADC-∠ACD= 50°,
∴∠CAE=∠DAE-∠CAD=15°,∴∠BAE=∠CAB-∠CAE=50°.
【B培优综合】
B11、如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
A.(0,1) B.(1,-1) C.(0,-1) D.(1,0)
试题分析:根据网格结构,找出对应点连线的垂直平分线的交点即为旋转中心.
试题解析:由图形可知,对应点的连线CC′、AA′的垂直平分线的交点是点(1,-1),根据旋转变换的
性质,点(1,-1)即为旋转中心.
故旋转中心坐标是P(1,-1).
故选B.
B12、如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,若使点D恰好落在BC上,则线段AP的长是( )
A.4 B.5 C.6 D.8
【分析】本题主要考查旋转的性质,全等三角形的判定与性质,等边三角形的性质,熟练掌握其知识点是解此题的关键.
根据题意通过“角角边”证明△AOP≌△CDO,进而得到AP=OC=AC﹣AO=6.
【详解】
解:根据题意可知:∠A=∠C=60°,
∵线段OP绕点O逆时针旋转得到线段OD,∴OP=DO,
∵∠DOP=60°,∴∠AOP+∠COD=∠CDO+∠COD=120°,∴∠AOP=∠CDO,
在△AOP与△CDO中,,∴△AOP≌△CDO(AAS),∴AP=OC=AC﹣AO=6.
故选C.
B13、如图,中,.将绕点B逆时针旋转得到,使点C的对应点恰好落在边上,则的度数是( )
A. B. C. D.
【分析】本题考查了旋转的性质,三角形的内角和定理,以及余角的性质,解题的关键是掌握所学的性质,正确求出.
由余角的性质,求出∠CAB=50°,由旋转的性质,得到,,然后求出,即可得到答案.
【详解】
解:在中,,∴∠CAB=50°,
由旋转的性质,则,,
∴,
∴;
故选:D.
B14、如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.当AD=BF时,∠BEF的度数是( )
A.45° B.60° C.62.5° D.67.5°
【分析】本题考查了旋转的性质、全等三角形的判定与性质以及等腰三角形的性质,解题的关键是熟练运用旋转的性质找出相等的线段和角,并能准确判定三角形全等,从而利用全等三角形性质解决相应的问题.
根据旋转的性质可得CD=CE和∠DCE=90°,结合∠ACB=90°,AC=BC,可证△ACD≌△BCE,依据全等三角形的性质即可得到∠CBE=∠A=45°,再由AD=BF可得等腰△BEF,则可计算出∠BEF的度数.
【详解】
解:由旋转性质可得: CD=CE,∠DCE=90°.
∵∠ACB=90°,AC=BC,∴∠A=45°.
∴∠ACB ∠DCB=∠DCE ∠DCB.即∠ACD=∠BCE.
∴△ACD≌△BCE.∴∠CBE=∠A=45°.
∵AD=BF,∴BE=BF.∴∠BEF=∠BFE= 67.5°.
故选:D.
B15、如图,在△BDE中,∠BDE=90°,BD=4,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转到 △ABC的位置,点C在BD上,则旋转中心的坐标为 __________ .
试题分析:根据旋转的性质,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴
于 F,再根据点C在BD上确定出∠PDB=45°并求出PD的长,然后求出∠PDO=60°,根据直角三角形两锐角互余求出∠DPF=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得DF=PD,利用勾股定理列式求出PF,再求出OF,即可得到点P,即旋转中心的坐标.
试题解析:如图,AB与BD的垂直平分线的交点即为旋转中心P,
连接PD,过P作PF⊥x轴于F,
∵点C在BD上,∴点P到AB、BD的距离相等,都是BD,即×4=2,
∴∠PDB=45°,PD=×2=4,
∵∠BDO=15°,∴∠PDO=45°+15°=60°,∴∠DPF=30°,∴DF=PD=×4=2,
∵点D的坐标是(5,0),∴OF=OD-DF=5-2=3,
由勾股定理得,PF===2,
∴旋转中心的坐标为(3,2).
故答案为:(3,2).
B16、如图,在中,,,将绕点逆时针旋转得到,连接,
(1) ,连接,则的长是 .
(2)求证:
(3)连接,求的长.
【答案】(1),;(2)见解析;(3)
【分析】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形.
(1)由旋转的性质可得BC=CN,∠BCN=60°=∠ACM,AC=CM,可得∠BCM=∠BCA+∠ACM=105°,△BCN是等边三角形,即可求解;
(2)可证△ACM是等边三角形,可得AM=CM,可证BM垂直平分AC,可得结论;
(3)连接AN,并延长AN交CM于H,可证AH垂直平分CM,可求NH和AH的长,即可求解.
【详解】
解:(1)连接BN,
∵∠ABC=90°,AB=BC=,∴∠ACB=∠BAC=45°,AC=AB=2,
∵将△ABC绕点C逆时针旋转60°得到△MNC,
∴BC=CN,∠BCN=60°=∠ACM,AC=CM,
∴∠BCM=∠BCA+∠ACM=105°,△BCN是等边三角形,∴BN=BC=,
故答案为:105°,;
(2)连接AM,
∵AC=CM,∠ACM=60°,∴△ACM是等边三角形,∴AM=CM,
又∵BC=BA,∴BM垂直平分AC,∴BM⊥AC;
(3)连接AN,并延长AN交CM于H,如图,
∵将△ABC绕点C逆时针旋转60°得到△MNC,
∴CA=CM=2,CN=MN=CB=AB=,∠ACM=60°,∠CNM=∠CBA=90°,
∴△ACM为等边三角形,∴AC=AM,
而NC=NM,∴AH垂直平分CM,
∴CH=NH=CM=1,AH=CH=,∴AN=AH-NH=-1.
【C拔尖拓展】
C17、(2021·四川广安·中考真题)如图,在平面直角坐标系中,轴,垂足为,将绕点逆时针旋转到的位置,使点的对应点落在直线上,再将绕点逆时针旋转到的位置,使点的对应点也落在直线上,以此进行下去……若点的坐标为,则点的纵坐标为______.
【分析】本题考查了一次函数图象上点的坐标特征,旋转以及直角三角形的性质,求出△OAB的各边,计算出OB21的长度是解题的关键.
计算出△AOB的各边,根据旋转的性质,求出OB1,B1B3,...,得出规律,求出OB21,再根据一次函数图像上的点求出点B21的纵坐标即可.
【详解】
解:∵AB⊥y轴,点B(0,3),
∴OB=3,则点A的纵坐标为3,代入,得:,得:x=-4,即A(-4,3),
∴OB=3,AB=4,OA==5,
由旋转可知:OB=O1B1=O2B1=O2B2=…=3,OA=O1A=O2A1=…=5,AB=AB1=A1B1=A2B2=…=4,
∴OB1=OA+AB1=4+5=9,B1B3=3+4+5=12,∴OB21=OB1+B1B21=9+(21-1)÷2×12=129,
设B21(a,),则OB21=,解得:或(舍),
则,即点B21的纵坐标为,
故答案为:.
C18、在平面直角坐标系中,四边形是矩形,点,点,点.以点为中心,顺时针旋转矩形,得到矩形,点的对应点分别为,记旋转角为.
(1)如图①,当时,求点的坐标;
(2)如图②,当点落在的延长线上时,求点的坐标;
(3)当点落在线段上时,求点的坐标(直接写出结果即可).
【答案】(1)点的坐标为;(2)点的坐标为;(3)点的坐标为.
【分析】本题考查的知识点是坐标系内矩形的旋转问题,用到的知识点有勾股定理,全等三角形的判定与性质等,做此类题目时往往需要利用数形结合的方法来求解,根据每一个问题做出不同的辅助线是解题的关键
(1) 过点作轴于根据已知条件可得出AD=6,再直角三角形ADG中可求出DG,AG的长,即可确定点D的坐标.
(2) 过点作轴于于可得出,根据勾股定理得出AE的长为10,再利用面积公式求出DH,从而求出OG,DG的长,得出答案
(3) 连接,作轴于G,由旋转性质得到,从而可证,继而可得出结论.
【详解】
解:(1)过点作轴于,如图①所示:
点,点.,
以点为中心,顺时针旋转矩形,得到矩形,
,
在中,,,
点的坐标为;
(2)过点作轴于于,如图②所示:则,
,,
,,
,,点的坐标为;
(3)连接,作轴于G,如图③所示:
由旋转的性质得:,
,,,
,,
在和中,,,
,,
点的坐标为.
(
1
)
-2021-2022学年八年级数学下册 (苏科版)
【A夯实基础】
A1、(1) 在平面内,将图形绕_______沿某个方向转动_________,这样的图形运动称为旋转。
(2)钟表上的指针随时间的变化而移动,这可以看作是数学上的__________。
(3)图形的旋转只改变图形的_________,而不改变图形的_______________。
(4)经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了_______的角度,任意一对对应点与旋转中心的连线所成的角都________,对应点到旋转中心的距离_________。
(5)△ABC绕一点旋转到△A' B' C',则△ABC和△A' B' C'的关系是__________。
A2、如图,ΔABP是由ΔACD按顺时针方向旋转某一角度得到的,若∠BAP=60°,则在这一旋转过程中,旋转中心是____________,旋转角度为____________.
A3、如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度到ABC的位置,使得点A,B,C在同一条直线上,那么这个角度等于( )
A .120° B .90° C .60° D .30°
A4、如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,
则旋转的角度为( )
A.30° B.45° C.90° D.135°
A5、分析图①、②、④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.
A6、画△ABC绕O点顺时针方向旋转90°后得到△A′B′C′.
A7、我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做
旋转,这个定点称为旋转中心,旋转的角度称为旋转角.如图,△ABC经过旋转得到△DEF.试用直
尺和圆规作出旋转中心(保留作图痕迹,不写作法).
A8、如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.点M B.格点N C.格点P D.格点Q
A9、在图中,将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是( )
A. B. C. D.
A10、如图,中,,在同一平面内,将绕点旋转到的位置,使得,求的度数
【B培优综合】
B11、如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
A.(0,1) B.(1,-1) C.(0,-1) D.(1,0)
B12、如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,若使点D恰好落在BC上,则线段AP的长是( )
A.4 B.5 C.6 D.8
B13、如图,中,.将绕点B逆时针旋转得到,使点C的对应点恰好落在边上,则的度数是( )
A. B. C. D.
B14、如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.当AD=BF时,∠BEF的度数是( )
A.45° B.60° C.62.5° D.67.5°
B15、如图,在△BDE中,∠BDE=90°,BD=4,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转到 △ABC的位置,点C在BD上,则旋转中心的坐标为 __________ .
B16、如图,在中,,,将绕点逆时针旋转得到,连接,
(1) ,连接,则的长是 .
(2)求证:
(3)连接,求的长.
【C拔尖拓展】
C17、(2021·四川广安·中考真题)如图,在平面直角坐标系中,轴,垂足为,将绕点逆时针旋转到的位置,使点的对应点落在直线上,再将绕点逆时针旋转到的位置,使点的对应点也落在直线上,以此进行下去……若点的坐标为,则点的纵坐标为______.
C18、在平面直角坐标系中,四边形是矩形,点,点,点.以点为中心,顺时针旋转矩形,得到矩形,点的对应点分别为,记旋转角为.
(1)如图①,当时,求点的坐标;
(2)如图②,当点落在的延长线上时,求点的坐标;
(3)当点落在线段上时,求点的坐标(直接写出结果即可).
9.1图形的旋转-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、(1) 在平面内,将图形绕_______沿某个方向转动_________,这样的图形运动称为旋转。
(2)钟表上的指针随时间的变化而移动,这可以看作是数学上的__________。
(3)图形的旋转只改变图形的_________,而不改变图形的_______________。
(4)经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了_______的角度,任意一对对应点与旋转中心的连线所成的角都________,对应点到旋转中心的距离_________。
(5)△ABC绕一点旋转到△A' B' C',则△ABC和△A' B' C'的关系是__________。
答案:(1)某个点;某个角度 (2)旋转 (3)位置;大小,形状
(4)相同;相等;相等 (5)全等
A2、如图,ΔABP是由ΔACD按顺时针方向旋转某一角度得到的,若∠BAP=60°,则在这一旋转过程中,旋转中心是____________,旋转角度为____________.
【分析】本题考查旋转的性质,明确旋转前后的图形大小和形状不变,正确确定对应角,对应边是解答此题的关键.
根据条件得出AD=AP,AC=AB,确定旋转中心,根据条件得出∠DAP=∠CAB=90°,确定旋转角度数.
【详解】
解:∵△ABP是由△ACD按顺时针方向旋转而得,
∴△ABP≌△ACD,
∴∠DAC=∠PAB=60°,AD=AP,AC=AB,
∴∠DAP=∠CAB=90°,
∴△ABP是△ACD以点A为旋转中心顺时针旋转90°得到的.
故答案为:A,90°
A3、如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度到ABC的位置,使得点A,B,C在同一条直线上,那么这个角度等于( )
A .120° B .90° C .60° D .30°
试题分析:利用旋转的性质计算.
解:∵∠ABC=60°,
∴旋转角∠CB=180°-60°=120°.
∴这个旋转角度等于120°.
故选:A.
A4、如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,
则旋转的角度为( )
A.30° B.45° C.90° D.135°
答案:C
试题分析:根据旋转的性质,对应边的夹角∠BOD即为旋转角.
∵△AOB绕点O按逆时针方向旋转到△COD的位置,
∴对应边OB、OD的夹角∠BOD即为旋转角,
∴旋转的角度为90°.
故选C.
A5、分析图①、②、④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.
分析:由①到②是旋转了90°,由②到④是旋转了180度,即通过两次旋转90度得到,据此即可判断.
解析:如图
A6、画△ABC绕O点顺时针方向旋转90°后得到△A′B′C′.
分析:根据旋转的性质,将A,B,C绕O点顺时针旋转90°,由此即可画出旋转后的图形.
解析:如图所示:
A7、我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做
旋转,这个定点称为旋转中心,旋转的角度称为旋转角.如图,△ABC经过旋转得到△DEF.试用直
尺和圆规作出旋转中心(保留作图痕迹,不写作法).
分析:根据旋转的性质,连接对应点AD、BE,再分别作AD、BE的垂直平分线,相交于点O,
则点O即为旋转中心.
解析:如图所示,点O即为△ABC旋转到△DEF的旋转中心.
A8、如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.点M B.格点N C.格点P D.格点Q
答案:B
试题分析:此题可根据旋转前后对应点到旋转中心的距离相等来判断所求的旋转中心.
试题解析:如图,连接N和两个三角形的对应点;
发现两个三角形的对应点到点N的距离相等,因此格点N就是所求的旋转中心;
故选B.
A9、在图中,将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是( )
A. B. C. D.
答案:B
分析:根据旋转的性质,找出图中三角形的关键处(旋转中心)按顺时针方向旋转90°后的形状即可选择答案.
解析:根据旋转的性质可知,绕O点顺时针旋转90°得到的图形是.
故选B.
A10、如图,中,,在同一平面内,将绕点旋转到的位置,使得,求的度数
【答案】∠BAE=50°
【分析】本题考查的是旋转变换,掌握平行线的性质、旋转变换的性质是解题的关键.
根据平行线的性质得到∠ACD=∠CAB=65°,根据旋转变换的性质计算即可.
【详解】
解:∵DC∥AB,∴∠ACD=∠CAB=65°,
由旋转的性质可知,AD=AC,∠DAE=∠CAB=65°,∴∠ADC=∠CAB=65°,
∴∠CAD=180°-∠ADC-∠ACD= 50°,
∴∠CAE=∠DAE-∠CAD=15°,∴∠BAE=∠CAB-∠CAE=50°.
【B培优综合】
B11、如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
A.(0,1) B.(1,-1) C.(0,-1) D.(1,0)
试题分析:根据网格结构,找出对应点连线的垂直平分线的交点即为旋转中心.
试题解析:由图形可知,对应点的连线CC′、AA′的垂直平分线的交点是点(1,-1),根据旋转变换的
性质,点(1,-1)即为旋转中心.
故旋转中心坐标是P(1,-1).
故选B.
B12、如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,若使点D恰好落在BC上,则线段AP的长是( )
A.4 B.5 C.6 D.8
【分析】本题主要考查旋转的性质,全等三角形的判定与性质,等边三角形的性质,熟练掌握其知识点是解此题的关键.
根据题意通过“角角边”证明△AOP≌△CDO,进而得到AP=OC=AC﹣AO=6.
【详解】
解:根据题意可知:∠A=∠C=60°,
∵线段OP绕点O逆时针旋转得到线段OD,∴OP=DO,
∵∠DOP=60°,∴∠AOP+∠COD=∠CDO+∠COD=120°,∴∠AOP=∠CDO,
在△AOP与△CDO中,,∴△AOP≌△CDO(AAS),∴AP=OC=AC﹣AO=6.
故选C.
B13、如图,中,.将绕点B逆时针旋转得到,使点C的对应点恰好落在边上,则的度数是( )
A. B. C. D.
【分析】本题考查了旋转的性质,三角形的内角和定理,以及余角的性质,解题的关键是掌握所学的性质,正确求出.
由余角的性质,求出∠CAB=50°,由旋转的性质,得到,,然后求出,即可得到答案.
【详解】
解:在中,,∴∠CAB=50°,
由旋转的性质,则,,
∴,
∴;
故选:D.
B14、如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.当AD=BF时,∠BEF的度数是( )
A.45° B.60° C.62.5° D.67.5°
【分析】本题考查了旋转的性质、全等三角形的判定与性质以及等腰三角形的性质,解题的关键是熟练运用旋转的性质找出相等的线段和角,并能准确判定三角形全等,从而利用全等三角形性质解决相应的问题.
根据旋转的性质可得CD=CE和∠DCE=90°,结合∠ACB=90°,AC=BC,可证△ACD≌△BCE,依据全等三角形的性质即可得到∠CBE=∠A=45°,再由AD=BF可得等腰△BEF,则可计算出∠BEF的度数.
【详解】
解:由旋转性质可得: CD=CE,∠DCE=90°.
∵∠ACB=90°,AC=BC,∴∠A=45°.
∴∠ACB ∠DCB=∠DCE ∠DCB.即∠ACD=∠BCE.
∴△ACD≌△BCE.∴∠CBE=∠A=45°.
∵AD=BF,∴BE=BF.∴∠BEF=∠BFE= 67.5°.
故选:D.
B15、如图,在△BDE中,∠BDE=90°,BD=4,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转到 △ABC的位置,点C在BD上,则旋转中心的坐标为 __________ .
试题分析:根据旋转的性质,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴
于 F,再根据点C在BD上确定出∠PDB=45°并求出PD的长,然后求出∠PDO=60°,根据直角三角形两锐角互余求出∠DPF=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得DF=PD,利用勾股定理列式求出PF,再求出OF,即可得到点P,即旋转中心的坐标.
试题解析:如图,AB与BD的垂直平分线的交点即为旋转中心P,
连接PD,过P作PF⊥x轴于F,
∵点C在BD上,∴点P到AB、BD的距离相等,都是BD,即×4=2,
∴∠PDB=45°,PD=×2=4,
∵∠BDO=15°,∴∠PDO=45°+15°=60°,∴∠DPF=30°,∴DF=PD=×4=2,
∵点D的坐标是(5,0),∴OF=OD-DF=5-2=3,
由勾股定理得,PF===2,
∴旋转中心的坐标为(3,2).
故答案为:(3,2).
B16、如图,在中,,,将绕点逆时针旋转得到,连接,
(1) ,连接,则的长是 .
(2)求证:
(3)连接,求的长.
【答案】(1),;(2)见解析;(3)
【分析】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形.
(1)由旋转的性质可得BC=CN,∠BCN=60°=∠ACM,AC=CM,可得∠BCM=∠BCA+∠ACM=105°,△BCN是等边三角形,即可求解;
(2)可证△ACM是等边三角形,可得AM=CM,可证BM垂直平分AC,可得结论;
(3)连接AN,并延长AN交CM于H,可证AH垂直平分CM,可求NH和AH的长,即可求解.
【详解】
解:(1)连接BN,
∵∠ABC=90°,AB=BC=,∴∠ACB=∠BAC=45°,AC=AB=2,
∵将△ABC绕点C逆时针旋转60°得到△MNC,
∴BC=CN,∠BCN=60°=∠ACM,AC=CM,
∴∠BCM=∠BCA+∠ACM=105°,△BCN是等边三角形,∴BN=BC=,
故答案为:105°,;
(2)连接AM,
∵AC=CM,∠ACM=60°,∴△ACM是等边三角形,∴AM=CM,
又∵BC=BA,∴BM垂直平分AC,∴BM⊥AC;
(3)连接AN,并延长AN交CM于H,如图,
∵将△ABC绕点C逆时针旋转60°得到△MNC,
∴CA=CM=2,CN=MN=CB=AB=,∠ACM=60°,∠CNM=∠CBA=90°,
∴△ACM为等边三角形,∴AC=AM,
而NC=NM,∴AH垂直平分CM,
∴CH=NH=CM=1,AH=CH=,∴AN=AH-NH=-1.
【C拔尖拓展】
C17、(2021·四川广安·中考真题)如图,在平面直角坐标系中,轴,垂足为,将绕点逆时针旋转到的位置,使点的对应点落在直线上,再将绕点逆时针旋转到的位置,使点的对应点也落在直线上,以此进行下去……若点的坐标为,则点的纵坐标为______.
【分析】本题考查了一次函数图象上点的坐标特征,旋转以及直角三角形的性质,求出△OAB的各边,计算出OB21的长度是解题的关键.
计算出△AOB的各边,根据旋转的性质,求出OB1,B1B3,...,得出规律,求出OB21,再根据一次函数图像上的点求出点B21的纵坐标即可.
【详解】
解:∵AB⊥y轴,点B(0,3),
∴OB=3,则点A的纵坐标为3,代入,得:,得:x=-4,即A(-4,3),
∴OB=3,AB=4,OA==5,
由旋转可知:OB=O1B1=O2B1=O2B2=…=3,OA=O1A=O2A1=…=5,AB=AB1=A1B1=A2B2=…=4,
∴OB1=OA+AB1=4+5=9,B1B3=3+4+5=12,∴OB21=OB1+B1B21=9+(21-1)÷2×12=129,
设B21(a,),则OB21=,解得:或(舍),
则,即点B21的纵坐标为,
故答案为:.
C18、在平面直角坐标系中,四边形是矩形,点,点,点.以点为中心,顺时针旋转矩形,得到矩形,点的对应点分别为,记旋转角为.
(1)如图①,当时,求点的坐标;
(2)如图②,当点落在的延长线上时,求点的坐标;
(3)当点落在线段上时,求点的坐标(直接写出结果即可).
【答案】(1)点的坐标为;(2)点的坐标为;(3)点的坐标为.
【分析】本题考查的知识点是坐标系内矩形的旋转问题,用到的知识点有勾股定理,全等三角形的判定与性质等,做此类题目时往往需要利用数形结合的方法来求解,根据每一个问题做出不同的辅助线是解题的关键
(1) 过点作轴于根据已知条件可得出AD=6,再直角三角形ADG中可求出DG,AG的长,即可确定点D的坐标.
(2) 过点作轴于于可得出,根据勾股定理得出AE的长为10,再利用面积公式求出DH,从而求出OG,DG的长,得出答案
(3) 连接,作轴于G,由旋转性质得到,从而可证,继而可得出结论.
【详解】
解:(1)过点作轴于,如图①所示:
点,点.,
以点为中心,顺时针旋转矩形,得到矩形,
,
在中,,,
点的坐标为;
(2)过点作轴于于,如图②所示:则,
,,
,,
,,点的坐标为;
(3)连接,作轴于G,如图③所示:
由旋转的性质得:,
,,,
,,
在和中,,,
,,
点的坐标为.
(
1
)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
