2021-2022学年苏科版数学八年级下册9.3平行四边形(1)课后补充习题分层练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级下册9.3平行四边形(1)课后补充习题分层练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 557.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 15:02:56 | ||
图片预览




文档简介
9.3平行四边形(1)-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)
【A夯实基础】
A1、已知在平行四边形ABCD中,∠A=∠B+40°,则∠A的度数为( )
A.35° B.70° C.110° D.140°
A2、下列关于平行四边形的特征的描述中,正确的个数有( )
(1)对边相等;(2)对角相等;(3)对角线相等;(4)邻边相等;(5)邻角互补.
A.2个 B.5个 C.3个 D.4个
A3、已知平行四边形的一边长为5,则对角线,的长可取下列数据中的( )
A.2和4 B.3和4 C.4和5 D.5和6
A4、与是平行四边形的一组对角,若,那么的度数是( )
A. B. C. D.
A5、如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BO的长为( )
A.5 B.8 C.10 D.11
A6、如图,中,对角线相交于点交于点,连接,若的周长为28,则的周长为( )
A.28 B.24 C.21 D.14
A7、如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=_____度.
A8、如图,在平行四边形ABCD中,AE、CF分别平分∠BAD和∠DCB,交对角线BD于点E、F.
(1)若∠BCF=55°,求∠ABC的度数;
(2)求证:BF=DE.
A9、如图,四边形ABCD为平行四边形,E,F是直线BD上两点,且BE=DF,连接AF,CE.
求证:∠E=∠F.
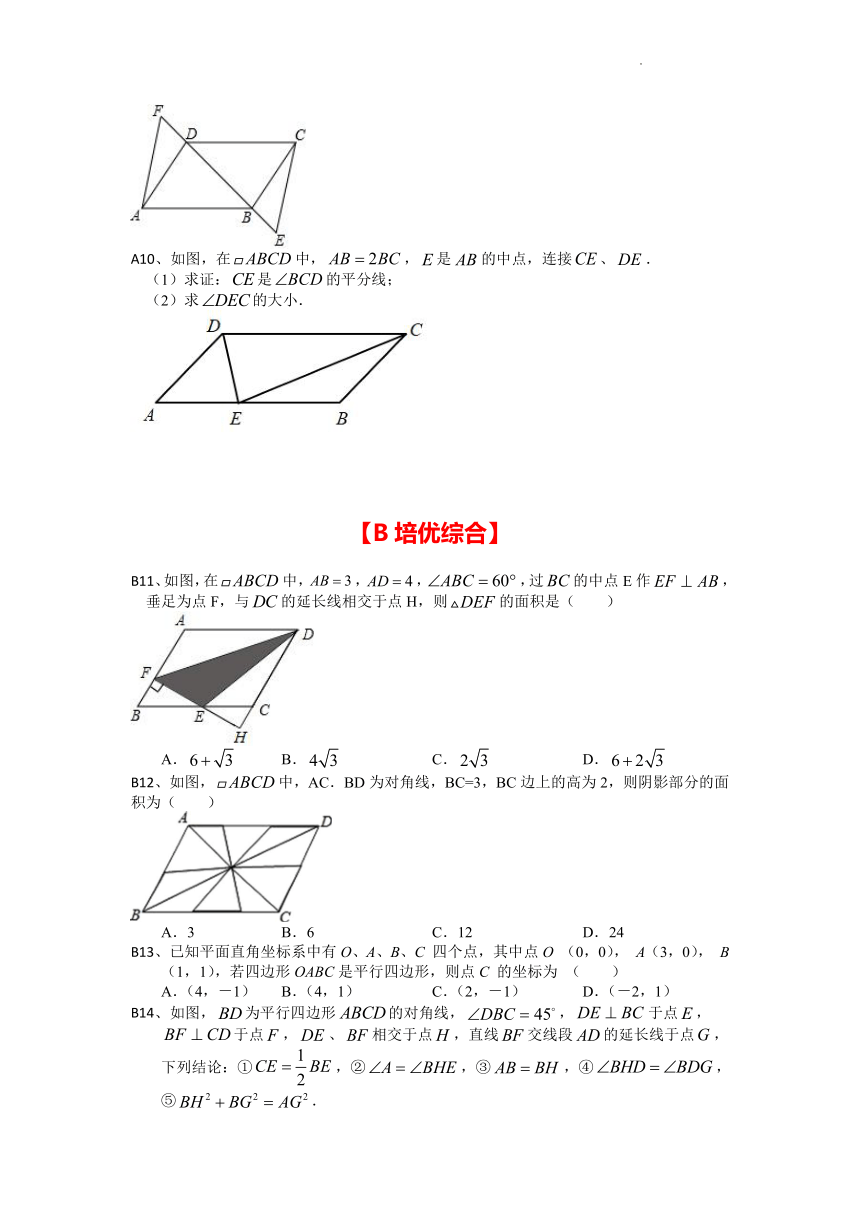
A10、如图,在中,,是的中点,连接、.
(1)求证:是的平分线;
(2)求的大小.
【B培优综合】
B11、如图,在中,,,,过的中点E作,垂足为点F,与的延长线相交于点H,则的面积是( )
A. B. C. D.
B12、如图,中,AC.BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
B13、已知平面直角坐标系中有O、A、B、C 四个点,其中点O (0,0), A(3,0), B(1,1),若四边形OABC是平行四边形,则点C 的坐标为 ( )
A.(4,-1) B.(4,1) C.(2,-1) D.(-2,1)
B14、如图,为平行四边形的对角线,,于点,于点,、相交于点,直线交线段的延长线于点,下列结论:①,②,③,④,⑤.
正确的结论有( )个
A.1 B.2 C.3 D.4
B15、(2021 柳南区校级模拟)如图,在中,点为上一点,连接并延长交的延长线于点,,连接.
(1)求证:平分;
(2)若点为中点,,,求的面积.
B16、如图,四边形ABCD是平行四边形,延长CB至点E,使得BE=BC,连结DE交AB于点F.
(1)求证:△ADF≌△BEF.
(2)连结DB,若AD=DB=5,CD=6,求DE的长.
【C拔尖拓展】
C17、如图,在平行四边形中,平分,交于点且,延长与的延长线相交于点,连接、.下列结论:①;②是等边三角形;③;④;⑤;其中正确的有( )
A.个 B.个 C.个 D.个
C18、如图①,在中,AB=3,AD=6.动点P沿AD边以每秒个单位长度的速度从点A向终点D运动.设点P运动的时间为秒.
(1)线段PD的长为_________(用含t的代数式表示).
(2)当CP平分∠BCD时,求t的值.
(3)如图②,另一动点Q以每秒2个单位长度的速度从点C出发,在CB上往返运动.P、Q两点同时出发,当点P停止运动时,点Q也随之停止运动。当以P、D、Q、B为顶点的四边形是平行四边形时,直接写出t的值.
9.3平行四边形(1)-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、已知在平行四边形ABCD中,∠A=∠B+40°,则∠A的度数为( )
A.35° B.70° C.110° D.140°
【答案】C
【分析】
根据题意得:∠A+∠B=180°,∠A=∠B+40°,代入解方程即可求得∠A的度数.
【详解】
解:∵四边形ABCD是平行四边形,∴AD∥BC, ∴∠A+∠B=180°,
∵∠A=∠B+40°,∴∠B+40°+∠B=180°,
∴∠B=70°,∴∠A=110°,
故选:C.
A2、下列关于平行四边形的特征的描述中,正确的个数有( )
(1)对边相等;(2)对角相等;(3)对角线相等;(4)邻边相等;(5)邻角互补.
A.2个 B.5个 C.3个 D.4个
【答案】C
【分析】
根据平行四边形的性质:平行四边形的对角相等,对角线互相平分,对边平行,即可判断各选项的正误.
【详解】
解:∵平行四边形的对角相等,对角线互相平分,对边平行,对边相等,邻角互补
可知(1)(2)(5)正确,
故选:C.
A3、已知平行四边形的一边长为5,则对角线,的长可取下列数据中的( )
A.2和4 B.3和4 C.4和5 D.5和6
【答案】D
【分析】
由三角形三边关系可得三角形两边之和大于第三边,两边之差小于第三边.
【详解】
解:由于两条对角线的一半与平行四边形的一边组成一个三角形,
所以(AC-BD)<5<(AC+BD),
由题中数据可得,AC和BD的长可取5和6,
故选D.
A4、与是平行四边形的一组对角,若,那么的度数是( )
A. B. C. D.
【答案】B
【分析】
根据平行四边形对角相等的性质可以得解.
【详解】
解:∵平行四边形的对角相等,∴∠C=∠A=60°
故选B.
A5、如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BO的长为( )
A.5 B.8 C.10 D.11
【答案】A
【分析】
根据平行四边形的性质可得AO=CO=AC=3,再利用勾股定理可得BO的长.
【详解】
解:∵四边形ABCD是平行四边形,∴AO=CO=AC=3,
∵AB⊥AC,AB=4,∴BO=,
故选:A.
A6、如图,中,对角线相交于点交于点,连接,若的周长为28,则的周长为( )
A.28 B.24 C.21 D.14
【答案】D
【分析】
根据平行四边形的性质OA=OC及OE⊥AC,可得AE=CE,从而△ADE的周长为AD+CD,由此可得结论.
【详解】
解:∵四边形ABCD是平行四边形,∴OA=OC
∵OE⊥AC,∴OE是线段AC的垂直平分线,∴AE=CE
∵平行四边形ABCD的周长为28,即2(AD+CD)=28, ∴AD+CD=14
∴△ADE的周长为:AD+DE+AE=AD+DE+CE=AD+CD=14
故选:D.
A7、如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=_____度.
【答案】20
【分析】本题考查了平行四边形的性质,解决本题的关键是利用三角形内角和定理,等边对等角等知识得到和所求角有关的角的度数.
由DB=DC,∠C=70°可以得到∠DBC=∠C=70°,又由AD∥BC推出∠ADB=∠DBC=∠C=70°,而∠AED=90°,由此可以求出∠DAE.
【详解】
解:∵DB=DC,∠C=70°,∴∠DBC=∠C=70°,
∵四边形ABCD是平行四边形,AE⊥BD,
∴AD∥BC, ∠AED=90°,∴∠ADB=∠DBC=∠C=70°,
∴∠DAE=90°﹣70°=20°.
故答案为:20.
A8、如图,在平行四边形ABCD中,AE、CF分别平分∠BAD和∠DCB,交对角线BD于点E、F.
(1)若∠BCF=55°,求∠ABC的度数;
(2)求证:BF=DE.
【答案】(1)70°;(2)见解析.
【分析】本题考查了平行四边形的性质、全等三角形的判定和性质以及平行线的性质等知识,熟练掌握平行四边形的性质,证明三角形全等是解题的关键,属于中考常考题型.
(1)先由平行四边形的性质得到AB∥CD,则∠ABC+∠BCD=180°,再由角平分线的定义得到∠BCD=2∠BCF,于是得到结论;
(2)先由平行四边形的性质得到AB∥CD,AB=CD,∠BAD=∠DCB,求得∠ABE=∠CDF,再证△ABE≌△CDF(ASA),然后由全等三角形的性质即可得到结论.
【详解】
(1)解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABC+∠BCD=180°,
∵CF平分∠DCB,∴∠BCD=2∠BCF,
∵∠BCF=55°,∴∠BCD=110°,∴∠ABC=180° 110°=70°;
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠DCB,∴∠ABE=∠CDF,
∵AE,CF分别平分∠BAD和∠DCB,∴∠BAE=∠BAD,∠DCF=∠DCB,
∴∠BAE=∠DCE,∴△ABE≌△CDF(ASA),∴BE=DF,∴BE+EF=DF+EF,即BF=DE.
A9、如图,四边形ABCD为平行四边形,E,F是直线BD上两点,且BE=DF,连接AF,CE.
求证:∠E=∠F.
【分析】本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题
证明△ADF≌△CBE(SAS),由全等三角形的性质即可解决问题.
【详解】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠ADB=∠DBC.
∵∠ADF+∠ADB=180°,∠CBE+∠DBC=180°
∴∠ADF=∠CBE.
在△ADF和△CBE中,,∴△ADF≌△CBE(SAS),∴∠E=∠F.
A10、如图,在中,,是的中点,连接、.
(1)求证:是的平分线;
(2)求的大小.
【答案】(1)见解析;(2)90°.
【分析】本题考查了平行四边形的性质,等腰三角形的性质.解题的关键是了解平行四边形的性质,难度不大.
(1)根据四边形ABCD是平行四边形得到∠DCE=∠CEB,然后根据AB=2BC,E是AB的中点得到∠CEB=∠ECB,等量代换可以得到∠DCE=∠BCE,从而证得CE是∠BCD的平分线;
(2)同理可得:DE平分∠ADC,然后根据两直线平行得到∠ADC+∠BCD=180°,从而得到∠EDC+∠ECD=90°,求得∠DEC=90°.
【详解】
解:(1)证明:在中,,为中点,
∴,,
∴,,
∴∴是的角平分线
(2)根据(1)同理可得:,
∵AD∥BC,∴∠ADC+∠BCD=180°,
∴∠EDC+∠ECD=90°,∴∠DEC=90°.
【B培优综合】
B11、如图,在中,,,,过的中点E作,垂足为点F,与的延长线相交于点H,则的面积是( )
A. B. C. D.
【答案】C
【分析】本题主要考查对平行四边形的性质,平行线的性质,勾股定理,含30度角的直角三角形,三角形的面积,三角形的内角和定理等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.
根据平行四边形的性质得到AB=CD=3,AD=BC=4,求出BE、BF、EF,根据相似得出CH=1,EH=,根据三角形的面积公式求△DFH的面积,即可求出答案.
【详解】
解:∵四边形ABCD是平行四边形,∴AD=BC=4,AB∥CD,AB=CD=3,
∵E为BC中点,∴BE=CE=2,
∵∠B=60°,EF⊥AB,∴∠FEB=30°,∴BF=1,
由勾股定理得:EF=,
∵AB∥CD,∴∠B=∠ECH,
在△BFE和△CHE中,,∴△BFE≌△CHE(ASA),
∴EF=EH=,CH=BF=1,∴DH=4,
∵S△DHF=DH FH=,∴S△DEF=S△DHF=,
故选:C.
B12、如图,中,AC.BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
【答案】A
【分析】
由中,AC.BD为对角线,BC=3,BC边上的高为2,即可求得平行四边形的面积,证明得(ASA),即可得,同理:
即可求得答案.
【详解】
解:如图,标注字母,
∵中,AC.BD为对角线,BC=3,BC边上的高为2,
∴,AD∥BC, OA=OC,
∠OAE=∠OCF,
在和中,, ∴(ASA), ∴,
同理:
故选:A.
B13、已知平面直角坐标系中有O、A、B、C 四个点,其中点O (0,0), A(3,0), B(1,1),若四边形OABC是平行四边形,则点C 的坐标为 ( )
A.(4,-1) B.(4,1) C.(2,-1) D.(-2,1)
【答案】D
【分析】
根据题意作图,根据平行四边形的性质即可求解.
【详解】
如图,∵四边形OABC是平行四边形,点O (0,0), A(3,0), B(1,1),
∴BC=AO=3,
故点C 的坐标为B(1-3,1),即(-2,1)
故选D.
B14、如图,为平行四边形的对角线,,于点,于点,、相交于点,直线交线段的延长线于点,下列结论:①,②,③,④,⑤.
正确的结论有( )个
A.1 B.2 C.3 D.4
【答案】C
【分析】
①先证明,再根据全等三角形的对应边相等解题;②先证明是等腰直角三角形,可证得,再根据平行四边形的对角相等解题;③根据平行四边形的性质解题;④由可证明,据此解题;⑤中,利用勾股定理解题.
【详解】
解::,是等腰直角三角形,
,
,
四边形是平行四边形,,,②正确;
在与中,,,
点不是中点,,①错误;
四边形是平行四边形,,,,③正确;
,,④错误;
,
中,
,,⑤正确,
②③⑤正确,
故选:C.
B15、(2021 柳南区校级模拟)如图,在中,点为上一点,连接并延长交的延长线于点,,连接.
(1)求证:平分;
(2)若点为中点,,,求的面积.
【分析】(1)根据平行四边形的性质得出,进而利用等腰三角形的性质解答即可;
(2)根据三角函数解答即可.
【解答】证明:(1)四边形是平行四边形,,,
,,
,即平分;
(2)四边形是平行四边形,,,,,
点为中点,,
,,
,边的高是,的面积.
B16、如图,四边形ABCD是平行四边形,延长CB至点E,使得BE=BC,连结DE交AB于点F.
(1)求证:△ADF≌△BEF.
(2)连结DB,若AD=DB=5,CD=6,求DE的长.
【答案】(1)见解析;(2)8
【分析】本题考查了平行四边形的性质、全等三角形的判定、平行线的性质、等腰三角形的性质、勾股定理等知识;熟练掌握平行四边形的性质,证明三角形全等是解题的关键.
(1)根据平行四边形的性质,证得∠ADF=∠E,AD=BE,∠A=∠FBE,再根据ASA判定全等即可;
(2)证明EF=DF,DB=BE,得出BF⊥DE,由勾股定理求出EF,即可得出结果.
【详解】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∴∠A=∠FBE,∠ADF=∠E
又∵BC=BE,∴AD=BE,
在△ADF和△BEF中,,∴△ADF≌△BEF(ASA);
(2)解:∵四边形ABCD是平行四边形,∴AB=CD=6,AD=BC,
由(1)得:△ADF≌△BEF,∴AD=BE,EF=DF,AF=BF=AB=3,
∵AD=DB=5,∴DB=BE=5,∴BF⊥DE,
在Rt△BEF中,EF===4,∴DE=2EF=2×4=8.
【C拔尖拓展】
C17、如图,在平行四边形中,平分,交于点且,延长与的延长线相交于点,连接、.下列结论:①;②是等边三角形;③;④;⑤;其中正确的有( )
A.个 B.个 C.个 D.个
【答案】B
【分析】
由平行四边形的性质和角平分线的定义得出∠BAE=∠BEA,得出AB=BE=AE,得出②正确;由△ABE是等边三角形得出∠ABE=∠EAD=60°,由SAS证明△ABC≌△EAD,得出①正确;由S△AEC=S△DEC,S△ABE=S△CEF得出⑤正确;③和④不正确.
【详解】
解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠EAD=∠AEB,
又∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠BEA,∴AB=BE,
∵AB=AE,∴△ABE是等边三角形;②正确;∴∠ABE=∠EAD=60°,
在△ABC和△EAD中,,∴△ABC≌△EAD(SAS);①正确;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,∴S△AEC=S△DEC,∴S△ABE=S△CEF;⑤正确.
若AD与BF相等,则BF=BC,
题中未限定这一条件,∴③不一定正确;
若S△BEF=S△ACD;则S△BEF=S△ABC,则AB=BF,
∴BF=BE,题中未限定这一条件,∴④不一定正确;
正确的有①②⑤.
故选:B.
C18、如图①,在中,AB=3,AD=6.动点P沿AD边以每秒个单位长度的速度从点A向终点D运动.设点P运动的时间为秒.
(1)线段PD的长为_________(用含t的代数式表示).
(2)当CP平分∠BCD时,求t的值.
(3)如图②,另一动点Q以每秒2个单位长度的速度从点C出发,在CB上往返运动.P、Q两点同时出发,当点P停止运动时,点Q也随之停止运动。当以P、D、Q、B为顶点的四边形是平行四边形时,直接写出t的值.
【答案】(1);(2);(3)4.8秒或7.2秒或9.6秒.
【分析】本题考查了平行四边形的性质,角平分线的定义,一元一次方程的应用,以及分类讨论的数学思想,分类讨论是解答本题的关键.
(1)直接根据PD=AD-AP求解即可;
(2)由平行线的性质和角平分线的定义证明∠DPC=∠DCP,得到DP=DC=3,然后列方程求解即可;
(3)分4中情况列一元一次方程求解即可.
【详解】
解:(1)PD=AD-AP=.
(2)∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB=3,∴∠DPC=∠BCP.
∵CP平分∠BCD,∴∠BCP=∠DCP, ∴∠DPC=∠DCP,
∴DP=DC=3, ∴, ∴;
(3)当0当3当6当9综上可知,t的值为4.8秒或7.2秒或9.6秒.
-2021-2022学年八年级数学下册 (苏科版)
【A夯实基础】
A1、已知在平行四边形ABCD中,∠A=∠B+40°,则∠A的度数为( )
A.35° B.70° C.110° D.140°
A2、下列关于平行四边形的特征的描述中,正确的个数有( )
(1)对边相等;(2)对角相等;(3)对角线相等;(4)邻边相等;(5)邻角互补.
A.2个 B.5个 C.3个 D.4个
A3、已知平行四边形的一边长为5,则对角线,的长可取下列数据中的( )
A.2和4 B.3和4 C.4和5 D.5和6
A4、与是平行四边形的一组对角,若,那么的度数是( )
A. B. C. D.
A5、如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BO的长为( )
A.5 B.8 C.10 D.11
A6、如图,中,对角线相交于点交于点,连接,若的周长为28,则的周长为( )
A.28 B.24 C.21 D.14
A7、如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=_____度.
A8、如图,在平行四边形ABCD中,AE、CF分别平分∠BAD和∠DCB,交对角线BD于点E、F.
(1)若∠BCF=55°,求∠ABC的度数;
(2)求证:BF=DE.
A9、如图,四边形ABCD为平行四边形,E,F是直线BD上两点,且BE=DF,连接AF,CE.
求证:∠E=∠F.
A10、如图,在中,,是的中点,连接、.
(1)求证:是的平分线;
(2)求的大小.
【B培优综合】
B11、如图,在中,,,,过的中点E作,垂足为点F,与的延长线相交于点H,则的面积是( )
A. B. C. D.
B12、如图,中,AC.BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
B13、已知平面直角坐标系中有O、A、B、C 四个点,其中点O (0,0), A(3,0), B(1,1),若四边形OABC是平行四边形,则点C 的坐标为 ( )
A.(4,-1) B.(4,1) C.(2,-1) D.(-2,1)
B14、如图,为平行四边形的对角线,,于点,于点,、相交于点,直线交线段的延长线于点,下列结论:①,②,③,④,⑤.
正确的结论有( )个
A.1 B.2 C.3 D.4
B15、(2021 柳南区校级模拟)如图,在中,点为上一点,连接并延长交的延长线于点,,连接.
(1)求证:平分;
(2)若点为中点,,,求的面积.
B16、如图,四边形ABCD是平行四边形,延长CB至点E,使得BE=BC,连结DE交AB于点F.
(1)求证:△ADF≌△BEF.
(2)连结DB,若AD=DB=5,CD=6,求DE的长.
【C拔尖拓展】
C17、如图,在平行四边形中,平分,交于点且,延长与的延长线相交于点,连接、.下列结论:①;②是等边三角形;③;④;⑤;其中正确的有( )
A.个 B.个 C.个 D.个
C18、如图①,在中,AB=3,AD=6.动点P沿AD边以每秒个单位长度的速度从点A向终点D运动.设点P运动的时间为秒.
(1)线段PD的长为_________(用含t的代数式表示).
(2)当CP平分∠BCD时,求t的值.
(3)如图②,另一动点Q以每秒2个单位长度的速度从点C出发,在CB上往返运动.P、Q两点同时出发,当点P停止运动时,点Q也随之停止运动。当以P、D、Q、B为顶点的四边形是平行四边形时,直接写出t的值.
9.3平行四边形(1)-课后补充习题分层练
-2021-2022学年八年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、已知在平行四边形ABCD中,∠A=∠B+40°,则∠A的度数为( )
A.35° B.70° C.110° D.140°
【答案】C
【分析】
根据题意得:∠A+∠B=180°,∠A=∠B+40°,代入解方程即可求得∠A的度数.
【详解】
解:∵四边形ABCD是平行四边形,∴AD∥BC, ∴∠A+∠B=180°,
∵∠A=∠B+40°,∴∠B+40°+∠B=180°,
∴∠B=70°,∴∠A=110°,
故选:C.
A2、下列关于平行四边形的特征的描述中,正确的个数有( )
(1)对边相等;(2)对角相等;(3)对角线相等;(4)邻边相等;(5)邻角互补.
A.2个 B.5个 C.3个 D.4个
【答案】C
【分析】
根据平行四边形的性质:平行四边形的对角相等,对角线互相平分,对边平行,即可判断各选项的正误.
【详解】
解:∵平行四边形的对角相等,对角线互相平分,对边平行,对边相等,邻角互补
可知(1)(2)(5)正确,
故选:C.
A3、已知平行四边形的一边长为5,则对角线,的长可取下列数据中的( )
A.2和4 B.3和4 C.4和5 D.5和6
【答案】D
【分析】
由三角形三边关系可得三角形两边之和大于第三边,两边之差小于第三边.
【详解】
解:由于两条对角线的一半与平行四边形的一边组成一个三角形,
所以(AC-BD)<5<(AC+BD),
由题中数据可得,AC和BD的长可取5和6,
故选D.
A4、与是平行四边形的一组对角,若,那么的度数是( )
A. B. C. D.
【答案】B
【分析】
根据平行四边形对角相等的性质可以得解.
【详解】
解:∵平行四边形的对角相等,∴∠C=∠A=60°
故选B.
A5、如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BO的长为( )
A.5 B.8 C.10 D.11
【答案】A
【分析】
根据平行四边形的性质可得AO=CO=AC=3,再利用勾股定理可得BO的长.
【详解】
解:∵四边形ABCD是平行四边形,∴AO=CO=AC=3,
∵AB⊥AC,AB=4,∴BO=,
故选:A.
A6、如图,中,对角线相交于点交于点,连接,若的周长为28,则的周长为( )
A.28 B.24 C.21 D.14
【答案】D
【分析】
根据平行四边形的性质OA=OC及OE⊥AC,可得AE=CE,从而△ADE的周长为AD+CD,由此可得结论.
【详解】
解:∵四边形ABCD是平行四边形,∴OA=OC
∵OE⊥AC,∴OE是线段AC的垂直平分线,∴AE=CE
∵平行四边形ABCD的周长为28,即2(AD+CD)=28, ∴AD+CD=14
∴△ADE的周长为:AD+DE+AE=AD+DE+CE=AD+CD=14
故选:D.
A7、如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=_____度.
【答案】20
【分析】本题考查了平行四边形的性质,解决本题的关键是利用三角形内角和定理,等边对等角等知识得到和所求角有关的角的度数.
由DB=DC,∠C=70°可以得到∠DBC=∠C=70°,又由AD∥BC推出∠ADB=∠DBC=∠C=70°,而∠AED=90°,由此可以求出∠DAE.
【详解】
解:∵DB=DC,∠C=70°,∴∠DBC=∠C=70°,
∵四边形ABCD是平行四边形,AE⊥BD,
∴AD∥BC, ∠AED=90°,∴∠ADB=∠DBC=∠C=70°,
∴∠DAE=90°﹣70°=20°.
故答案为:20.
A8、如图,在平行四边形ABCD中,AE、CF分别平分∠BAD和∠DCB,交对角线BD于点E、F.
(1)若∠BCF=55°,求∠ABC的度数;
(2)求证:BF=DE.
【答案】(1)70°;(2)见解析.
【分析】本题考查了平行四边形的性质、全等三角形的判定和性质以及平行线的性质等知识,熟练掌握平行四边形的性质,证明三角形全等是解题的关键,属于中考常考题型.
(1)先由平行四边形的性质得到AB∥CD,则∠ABC+∠BCD=180°,再由角平分线的定义得到∠BCD=2∠BCF,于是得到结论;
(2)先由平行四边形的性质得到AB∥CD,AB=CD,∠BAD=∠DCB,求得∠ABE=∠CDF,再证△ABE≌△CDF(ASA),然后由全等三角形的性质即可得到结论.
【详解】
(1)解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABC+∠BCD=180°,
∵CF平分∠DCB,∴∠BCD=2∠BCF,
∵∠BCF=55°,∴∠BCD=110°,∴∠ABC=180° 110°=70°;
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠DCB,∴∠ABE=∠CDF,
∵AE,CF分别平分∠BAD和∠DCB,∴∠BAE=∠BAD,∠DCF=∠DCB,
∴∠BAE=∠DCE,∴△ABE≌△CDF(ASA),∴BE=DF,∴BE+EF=DF+EF,即BF=DE.
A9、如图,四边形ABCD为平行四边形,E,F是直线BD上两点,且BE=DF,连接AF,CE.
求证:∠E=∠F.
【分析】本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题
证明△ADF≌△CBE(SAS),由全等三角形的性质即可解决问题.
【详解】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠ADB=∠DBC.
∵∠ADF+∠ADB=180°,∠CBE+∠DBC=180°
∴∠ADF=∠CBE.
在△ADF和△CBE中,,∴△ADF≌△CBE(SAS),∴∠E=∠F.
A10、如图,在中,,是的中点,连接、.
(1)求证:是的平分线;
(2)求的大小.
【答案】(1)见解析;(2)90°.
【分析】本题考查了平行四边形的性质,等腰三角形的性质.解题的关键是了解平行四边形的性质,难度不大.
(1)根据四边形ABCD是平行四边形得到∠DCE=∠CEB,然后根据AB=2BC,E是AB的中点得到∠CEB=∠ECB,等量代换可以得到∠DCE=∠BCE,从而证得CE是∠BCD的平分线;
(2)同理可得:DE平分∠ADC,然后根据两直线平行得到∠ADC+∠BCD=180°,从而得到∠EDC+∠ECD=90°,求得∠DEC=90°.
【详解】
解:(1)证明:在中,,为中点,
∴,,
∴,,
∴∴是的角平分线
(2)根据(1)同理可得:,
∵AD∥BC,∴∠ADC+∠BCD=180°,
∴∠EDC+∠ECD=90°,∴∠DEC=90°.
【B培优综合】
B11、如图,在中,,,,过的中点E作,垂足为点F,与的延长线相交于点H,则的面积是( )
A. B. C. D.
【答案】C
【分析】本题主要考查对平行四边形的性质,平行线的性质,勾股定理,含30度角的直角三角形,三角形的面积,三角形的内角和定理等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.
根据平行四边形的性质得到AB=CD=3,AD=BC=4,求出BE、BF、EF,根据相似得出CH=1,EH=,根据三角形的面积公式求△DFH的面积,即可求出答案.
【详解】
解:∵四边形ABCD是平行四边形,∴AD=BC=4,AB∥CD,AB=CD=3,
∵E为BC中点,∴BE=CE=2,
∵∠B=60°,EF⊥AB,∴∠FEB=30°,∴BF=1,
由勾股定理得:EF=,
∵AB∥CD,∴∠B=∠ECH,
在△BFE和△CHE中,,∴△BFE≌△CHE(ASA),
∴EF=EH=,CH=BF=1,∴DH=4,
∵S△DHF=DH FH=,∴S△DEF=S△DHF=,
故选:C.
B12、如图,中,AC.BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
【答案】A
【分析】
由中,AC.BD为对角线,BC=3,BC边上的高为2,即可求得平行四边形的面积,证明得(ASA),即可得,同理:
即可求得答案.
【详解】
解:如图,标注字母,
∵中,AC.BD为对角线,BC=3,BC边上的高为2,
∴,AD∥BC, OA=OC,
∠OAE=∠OCF,
在和中,, ∴(ASA), ∴,
同理:
故选:A.
B13、已知平面直角坐标系中有O、A、B、C 四个点,其中点O (0,0), A(3,0), B(1,1),若四边形OABC是平行四边形,则点C 的坐标为 ( )
A.(4,-1) B.(4,1) C.(2,-1) D.(-2,1)
【答案】D
【分析】
根据题意作图,根据平行四边形的性质即可求解.
【详解】
如图,∵四边形OABC是平行四边形,点O (0,0), A(3,0), B(1,1),
∴BC=AO=3,
故点C 的坐标为B(1-3,1),即(-2,1)
故选D.
B14、如图,为平行四边形的对角线,,于点,于点,、相交于点,直线交线段的延长线于点,下列结论:①,②,③,④,⑤.
正确的结论有( )个
A.1 B.2 C.3 D.4
【答案】C
【分析】
①先证明,再根据全等三角形的对应边相等解题;②先证明是等腰直角三角形,可证得,再根据平行四边形的对角相等解题;③根据平行四边形的性质解题;④由可证明,据此解题;⑤中,利用勾股定理解题.
【详解】
解::,是等腰直角三角形,
,
,
四边形是平行四边形,,,②正确;
在与中,,,
点不是中点,,①错误;
四边形是平行四边形,,,,③正确;
,,④错误;
,
中,
,,⑤正确,
②③⑤正确,
故选:C.
B15、(2021 柳南区校级模拟)如图,在中,点为上一点,连接并延长交的延长线于点,,连接.
(1)求证:平分;
(2)若点为中点,,,求的面积.
【分析】(1)根据平行四边形的性质得出,进而利用等腰三角形的性质解答即可;
(2)根据三角函数解答即可.
【解答】证明:(1)四边形是平行四边形,,,
,,
,即平分;
(2)四边形是平行四边形,,,,,
点为中点,,
,,
,边的高是,的面积.
B16、如图,四边形ABCD是平行四边形,延长CB至点E,使得BE=BC,连结DE交AB于点F.
(1)求证:△ADF≌△BEF.
(2)连结DB,若AD=DB=5,CD=6,求DE的长.
【答案】(1)见解析;(2)8
【分析】本题考查了平行四边形的性质、全等三角形的判定、平行线的性质、等腰三角形的性质、勾股定理等知识;熟练掌握平行四边形的性质,证明三角形全等是解题的关键.
(1)根据平行四边形的性质,证得∠ADF=∠E,AD=BE,∠A=∠FBE,再根据ASA判定全等即可;
(2)证明EF=DF,DB=BE,得出BF⊥DE,由勾股定理求出EF,即可得出结果.
【详解】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∴∠A=∠FBE,∠ADF=∠E
又∵BC=BE,∴AD=BE,
在△ADF和△BEF中,,∴△ADF≌△BEF(ASA);
(2)解:∵四边形ABCD是平行四边形,∴AB=CD=6,AD=BC,
由(1)得:△ADF≌△BEF,∴AD=BE,EF=DF,AF=BF=AB=3,
∵AD=DB=5,∴DB=BE=5,∴BF⊥DE,
在Rt△BEF中,EF===4,∴DE=2EF=2×4=8.
【C拔尖拓展】
C17、如图,在平行四边形中,平分,交于点且,延长与的延长线相交于点,连接、.下列结论:①;②是等边三角形;③;④;⑤;其中正确的有( )
A.个 B.个 C.个 D.个
【答案】B
【分析】
由平行四边形的性质和角平分线的定义得出∠BAE=∠BEA,得出AB=BE=AE,得出②正确;由△ABE是等边三角形得出∠ABE=∠EAD=60°,由SAS证明△ABC≌△EAD,得出①正确;由S△AEC=S△DEC,S△ABE=S△CEF得出⑤正确;③和④不正确.
【详解】
解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠EAD=∠AEB,
又∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠BEA,∴AB=BE,
∵AB=AE,∴△ABE是等边三角形;②正确;∴∠ABE=∠EAD=60°,
在△ABC和△EAD中,,∴△ABC≌△EAD(SAS);①正确;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,∴S△AEC=S△DEC,∴S△ABE=S△CEF;⑤正确.
若AD与BF相等,则BF=BC,
题中未限定这一条件,∴③不一定正确;
若S△BEF=S△ACD;则S△BEF=S△ABC,则AB=BF,
∴BF=BE,题中未限定这一条件,∴④不一定正确;
正确的有①②⑤.
故选:B.
C18、如图①,在中,AB=3,AD=6.动点P沿AD边以每秒个单位长度的速度从点A向终点D运动.设点P运动的时间为秒.
(1)线段PD的长为_________(用含t的代数式表示).
(2)当CP平分∠BCD时,求t的值.
(3)如图②,另一动点Q以每秒2个单位长度的速度从点C出发,在CB上往返运动.P、Q两点同时出发,当点P停止运动时,点Q也随之停止运动。当以P、D、Q、B为顶点的四边形是平行四边形时,直接写出t的值.
【答案】(1);(2);(3)4.8秒或7.2秒或9.6秒.
【分析】本题考查了平行四边形的性质,角平分线的定义,一元一次方程的应用,以及分类讨论的数学思想,分类讨论是解答本题的关键.
(1)直接根据PD=AD-AP求解即可;
(2)由平行线的性质和角平分线的定义证明∠DPC=∠DCP,得到DP=DC=3,然后列方程求解即可;
(3)分4中情况列一元一次方程求解即可.
【详解】
解:(1)PD=AD-AP=.
(2)∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB=3,∴∠DPC=∠BCP.
∵CP平分∠BCD,∴∠BCP=∠DCP, ∴∠DPC=∠DCP,
∴DP=DC=3, ∴, ∴;
(3)当0
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
