27.2.1相似三角形的判定(第一课时)
文档属性
| 名称 | 27.2.1相似三角形的判定(第一课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-17 00:00:00 | ||
图片预览


文档简介
课件17张PPT。27.2.1相似三角形的判定
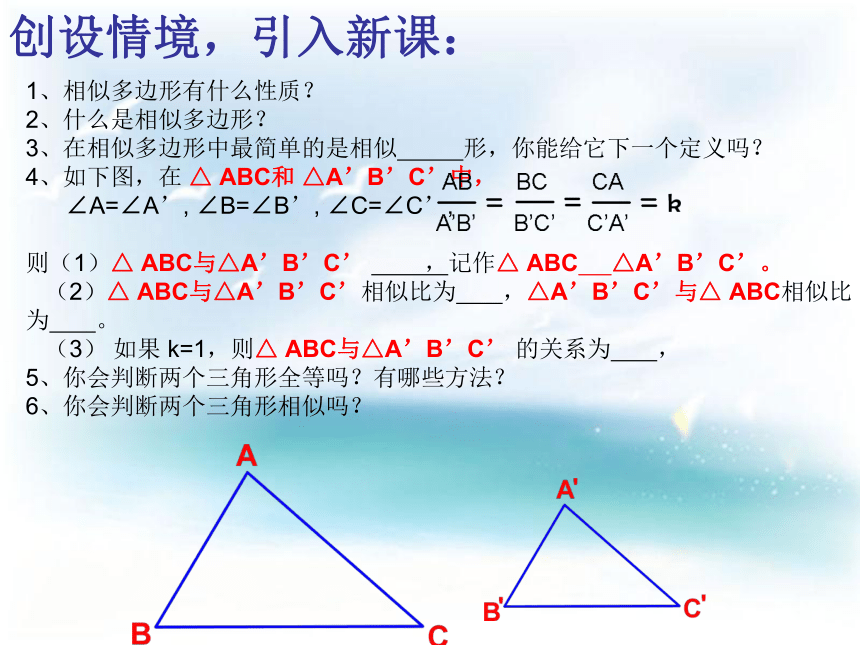
(第1课时)创设情境,引入新课:1、相似多边形有什么性质?
2、什么是相似多边形?
3、在相似多边形中最简单的是相似 形,你能给它下一个定义吗?
4、如下图,在 △ ABC和 △A’B’C’中,
∠A=∠A’, ∠B=∠B’, ∠C=∠C’,
则(1)△ ABC与△A’B’C’ ,记作△ ABC △A’B’C’。
(2)△ ABC与△A’B’C’相似比为 ,△A’B’C’与△ ABC相似比为 。
(3) 如果 k=1,则△ ABC与△A’B’C’ 的关系为 ,
5、你会判断两个三角形全等吗?有哪些方法?
6、你会判断两个三角形相似吗? 探究活动1:
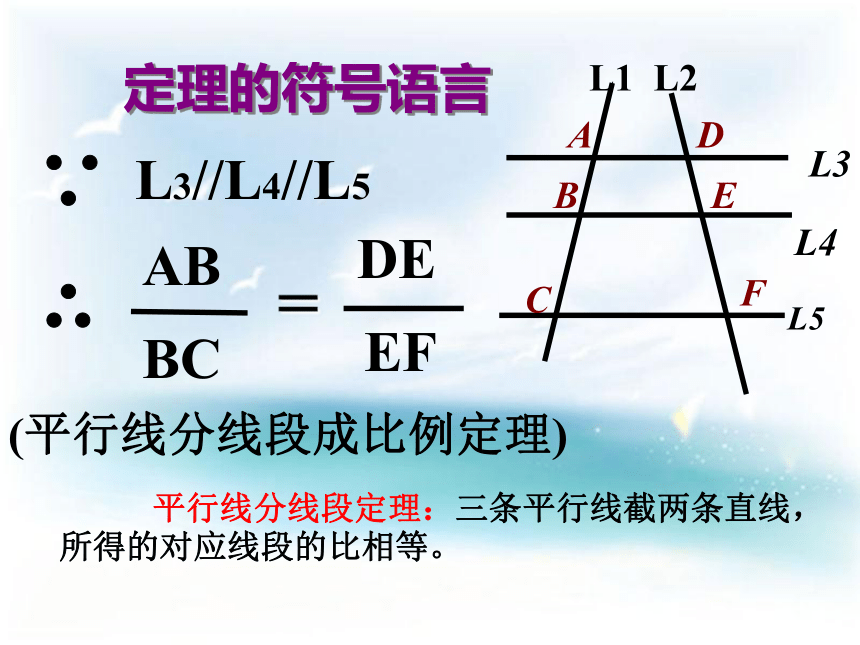
如图,任意画两条直线l1、l2,再画三条与l1、l2相交的平行线l3、l4 、l5。
分别度量l3、l4 、l5在l1上截得的两条线段AB,BC和在l2上截得的
两条线段DE、EF的长度,
(1) 与 相等吗?
(2)任意平移l5,在度量AB、BC、DE、EF的长度, 与 相等吗?
(3)在图中 是否也相等呢?
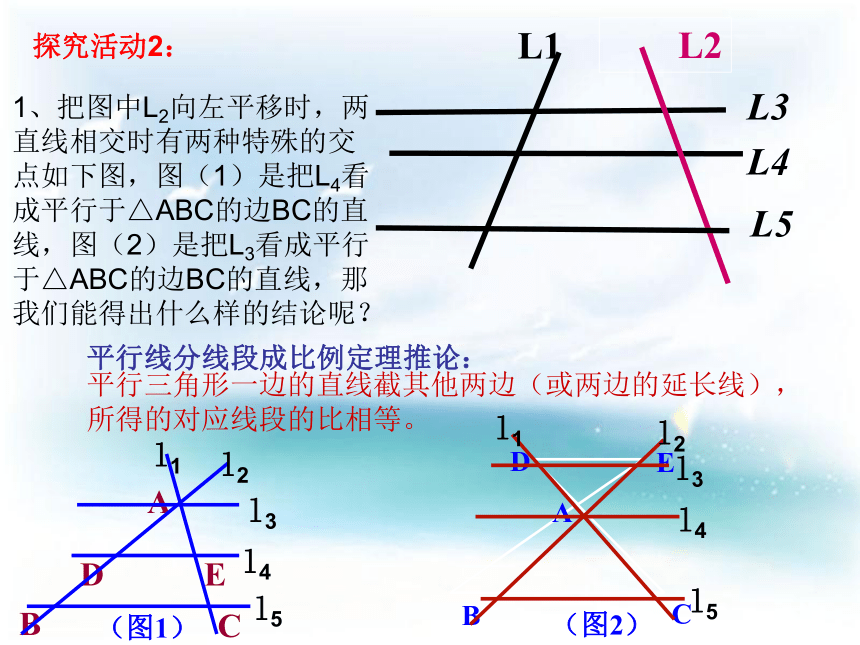
(4)由此你能得出什么样的结论?合作交流,探究新知:l1l2l3l4ABDE三条平行线截两条直线,所得的对应线段的比相等。平行线分线段成比例定理: 平行线分线段定理:三条平行线截两条直线,所得的对应线段的比相等。探究活动2:L3L4L5L11、把图中L2向左平移时,两直线相交时有两种特殊的交点如下图,图(1)是把L4看成平行于△ABC的边BC的直线,图(2)是把L3看成平行于△ABC的边BC的直线,那我们能得出什么样的结论呢?平行三角形一边的直线截其他两边(或两边的延长线),
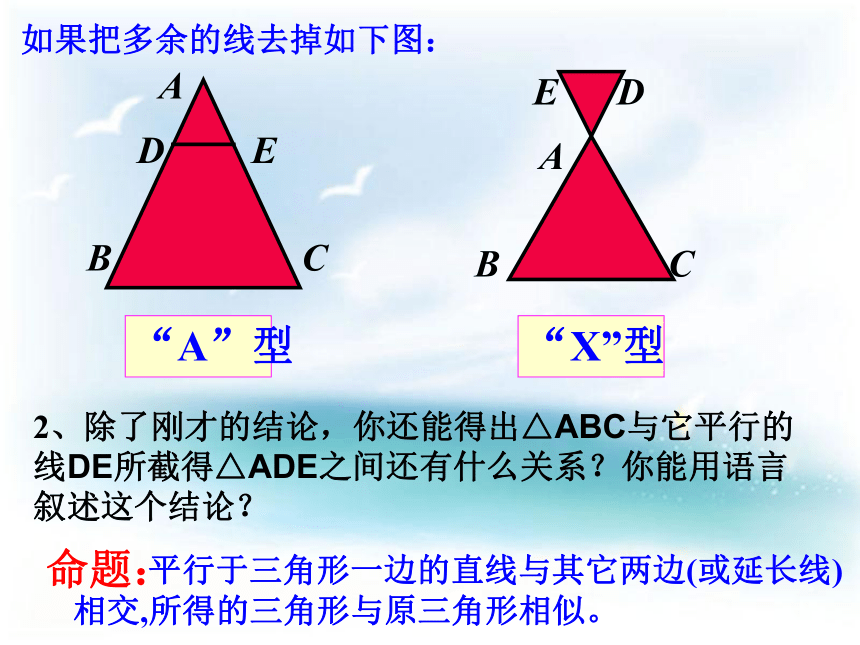
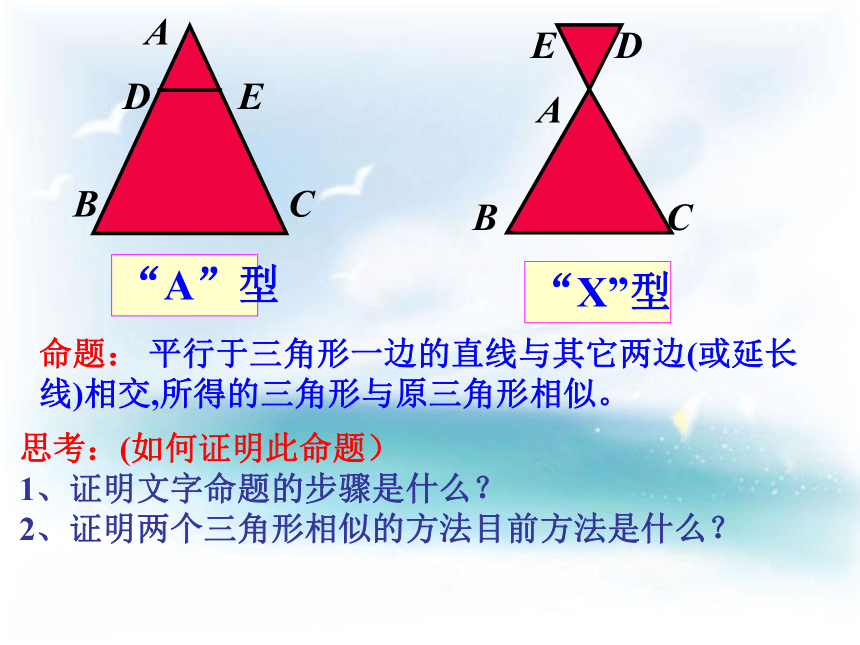
所得的对应线段的比相等。平行线分线段成比例定理推论: 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。“A”型 “X”型 命题: 如果把多余的线去掉如下图:2、除了刚才的结论,你还能得出△ABC与它平行的线DE所截得△ADE之间还有什么关系?你能用语言叙述这个结论?命题: 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。“A”型 “X”型 思考:(如何证明此命题)
1、证明文字命题的步骤是什么?
2、证明两个三角形相似的方法目前方法是什么? 1. 如图,已知:DE//BC,
求证: △ADE∽△ABCABCDE证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F∵四边形DBFE是平行四边形F∴DE=BF∴△ADE∽△ABC2. 如图,已知:DE//BC,
求证: △ADE与△ABCFFG方法一:延长BC,过点E作EF//DB,
方法二:在AB上截取AF=AD,过点F作FG//DE,证△ADE ≌ △A FG 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。三角形相似的(预备)定理:∵ DE∥BC
∵ DE∥BC
数学符号语言数学符号语言“A”型 “X”型 总结: 预备定理:平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。自我尝试: 1、 如图 请尽可能多地找出下列图中的
相似三角形,并说明理由。DE∥BC ,DF∥AC,图1图2图3DE∥FG//BC AB∥EF∥CD,2、如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)解: (1)DE ∥ BC△ADE∽△ABC∠AED=∠C=400.△ADE∽△ABC在△ADE中, ∠ADE=1800-400-450=950.(3)求△ABC与△ADE的相似比?例:如图,小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h。
(设网球是直线运动)图中有几个相似三角形?应用提高:重心的性质:三角形的重心到一个顶点的距离,等于它到对边中点的距离的两倍。 1、“三角形相似的预备定理”。这个定理揭示了有三角形一边的平行线,必构成相似三角形, 因此在三角形相似的解题中,常作平行线构造三角形与已知三角形相似。
2、相似比是带有顺序性和对应性的。拓展提升:1、本节课你的收获是什么?疑惑是什么?课堂小结:2、本节课你学到了什么样解决问题的方法?作业:课本54页第4,5 题.再见
(第1课时)创设情境,引入新课:1、相似多边形有什么性质?
2、什么是相似多边形?
3、在相似多边形中最简单的是相似 形,你能给它下一个定义吗?
4、如下图,在 △ ABC和 △A’B’C’中,
∠A=∠A’, ∠B=∠B’, ∠C=∠C’,
则(1)△ ABC与△A’B’C’ ,记作△ ABC △A’B’C’。
(2)△ ABC与△A’B’C’相似比为 ,△A’B’C’与△ ABC相似比为 。
(3) 如果 k=1,则△ ABC与△A’B’C’ 的关系为 ,
5、你会判断两个三角形全等吗?有哪些方法?
6、你会判断两个三角形相似吗? 探究活动1:
如图,任意画两条直线l1、l2,再画三条与l1、l2相交的平行线l3、l4 、l5。
分别度量l3、l4 、l5在l1上截得的两条线段AB,BC和在l2上截得的
两条线段DE、EF的长度,
(1) 与 相等吗?
(2)任意平移l5,在度量AB、BC、DE、EF的长度, 与 相等吗?
(3)在图中 是否也相等呢?
(4)由此你能得出什么样的结论?合作交流,探究新知:l1l2l3l4ABDE三条平行线截两条直线,所得的对应线段的比相等。平行线分线段成比例定理: 平行线分线段定理:三条平行线截两条直线,所得的对应线段的比相等。探究活动2:L3L4L5L11、把图中L2向左平移时,两直线相交时有两种特殊的交点如下图,图(1)是把L4看成平行于△ABC的边BC的直线,图(2)是把L3看成平行于△ABC的边BC的直线,那我们能得出什么样的结论呢?平行三角形一边的直线截其他两边(或两边的延长线),
所得的对应线段的比相等。平行线分线段成比例定理推论: 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。“A”型 “X”型 命题: 如果把多余的线去掉如下图:2、除了刚才的结论,你还能得出△ABC与它平行的线DE所截得△ADE之间还有什么关系?你能用语言叙述这个结论?命题: 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。“A”型 “X”型 思考:(如何证明此命题)
1、证明文字命题的步骤是什么?
2、证明两个三角形相似的方法目前方法是什么? 1. 如图,已知:DE//BC,
求证: △ADE∽△ABCABCDE证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F∵四边形DBFE是平行四边形F∴DE=BF∴△ADE∽△ABC2. 如图,已知:DE//BC,
求证: △ADE与△ABCFFG方法一:延长BC,过点E作EF//DB,
方法二:在AB上截取AF=AD,过点F作FG//DE,证△ADE ≌ △A FG 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。三角形相似的(预备)定理:∵ DE∥BC
∵ DE∥BC
数学符号语言数学符号语言“A”型 “X”型 总结: 预备定理:平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。自我尝试: 1、 如图 请尽可能多地找出下列图中的
相似三角形,并说明理由。DE∥BC ,DF∥AC,图1图2图3DE∥FG//BC AB∥EF∥CD,2、如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)解: (1)DE ∥ BC△ADE∽△ABC∠AED=∠C=400.△ADE∽△ABC在△ADE中, ∠ADE=1800-400-450=950.(3)求△ABC与△ADE的相似比?例:如图,小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h。
(设网球是直线运动)图中有几个相似三角形?应用提高:重心的性质:三角形的重心到一个顶点的距离,等于它到对边中点的距离的两倍。 1、“三角形相似的预备定理”。这个定理揭示了有三角形一边的平行线,必构成相似三角形, 因此在三角形相似的解题中,常作平行线构造三角形与已知三角形相似。
2、相似比是带有顺序性和对应性的。拓展提升:1、本节课你的收获是什么?疑惑是什么?课堂小结:2、本节课你学到了什么样解决问题的方法?作业:课本54页第4,5 题.再见
