苏科版七年级数学下册 第7章 小结与思考 课件(共29张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 第7章 小结与思考 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 177.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 08:10:02 | ||
图片预览






文档简介
(共29张PPT)
小结与思考
a
b
c
d
a
b
a
b
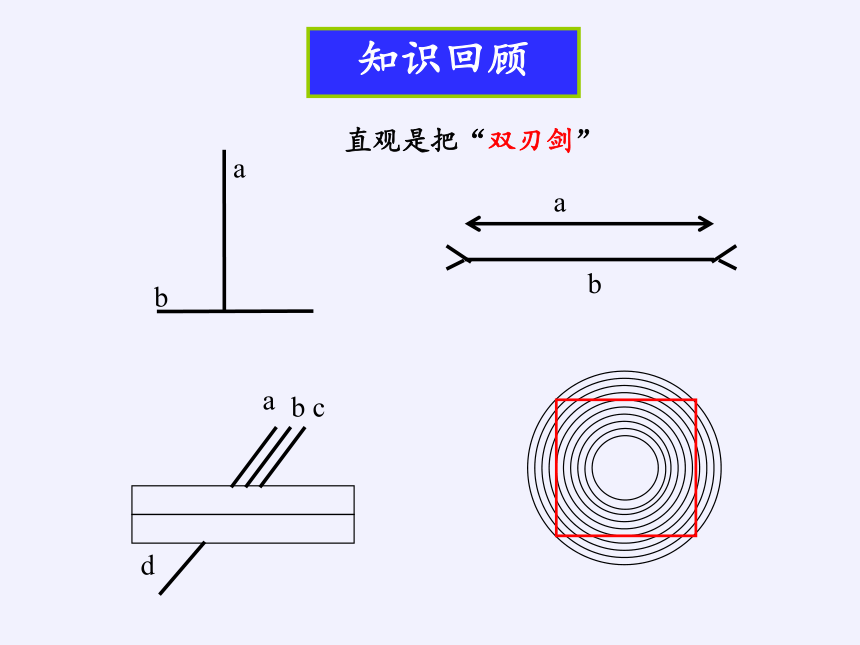
直观是把“双刃剑”
知识回顾
判断正误
观察.实验.操作
说理
证明
基本事实
定理
推论
真命题
假命题
原命题
逆命题
举反例
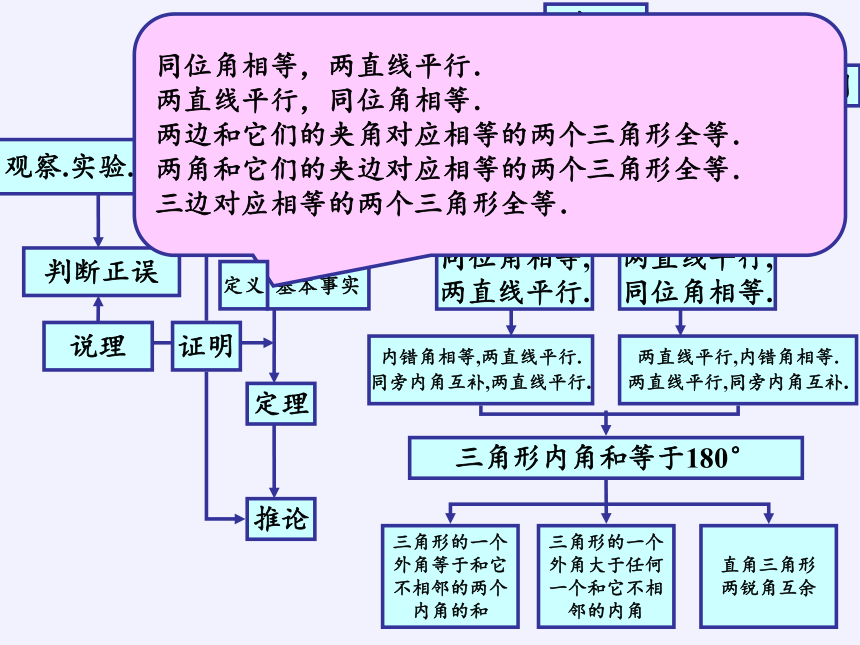
同位角相等,
两直线平行.
两直线平行,
同位角相等.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
三角形内角和等于180°
三角形的一个
外角等于和它
不相邻的两个
内角的和
三角形的一个
外角大于任何
一个和它不相
邻的内角
直角三角形
两锐角互余
命题
同位角相等,两直线平行.
两直线平行,同位角相等.
两边和它们的夹角对应相等的两个三角形全等.
两角和它们的夹边对应相等的两个三角形全等.
三边对应相等的两个三角形全等.
定义
学好几何的标志是会“证明”
证明命题的一般步骤:
根据命题,画出图形;
根据命题,结合图形,写出已知、求证;
写出证明过程.
注:运用数学符号和数学语言条理清晰地写出证明过程;
检查表达过程是否正确,完善。
知识回顾
对名称或术语的含义进行描述,做出规定,就是给出他们的定义.
“能够完全重合的图形”是“_______”的定义.
例如:
“符号不同、绝对值相等的两个数”是“ ”的定义;
互为相反数
全等形
无理数:
直角三角形:
无限不循环小数叫做无理数.
有一个角是直角的三角形叫做直角三角形.
知识回顾
正确的命题称为真命题,
不正确的的命题称为假命题.
命题:判断一件事情的句子,叫做命题.
命题由条件和结论两部分构成.
知识回顾
下面的句子哪些是命题
(1)每单位面积所受到的压力叫做压强;
(2)如果a是实数,那么a2+1〉0;
(3)两个无理数的乘积一定是无理数;
(4)偶数一定是合数吗?
(5)连接AB;
(6)不相等的两个角不可能是对顶角
练 一 练
对于命题“不相等的两个角不可能是对顶角”
条件:
结论:
改写成“如果……,那么……”的形式:
两个角不相等
这两个角不可能是对顶角
如果两个角不相等,那么这两个角不可能是对顶角
(3)两个无理数的乘积一定是无理数;
练 一 练
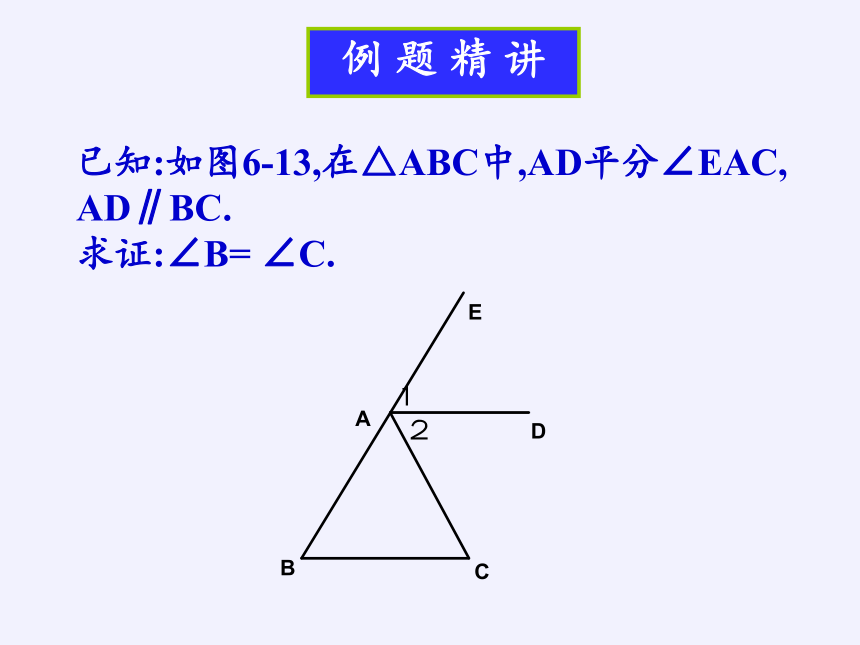
已知:如图6-13,在△ABC中,AD平分∠EAC, AD∥BC.
求证:∠B= ∠C.
1
2
例 题 精 讲
三角形内角和定理
例 题 精 讲
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
例 题 精 讲
如图. ∠1是△ABC的一个外角, ∠1与图中的其它角有什么关系
∠1+∠4=1800 ;
∠1=∠2+∠3;
∠1>∠ 2;
∠1>∠ 3.
A
B
C
D
1
2
3
4
例 题 精 讲
三角形内角和定理
已知:如图,已知AD是△ABD 和△ACD的公共边,求证:∠BDC=∠BAC+∠B+∠C
A
B
C
D
你还有其他方法解决这个问题吗
例 题 精 讲
你能把命题中的条件和结论互换, 构造一个新的命题吗
D
你构造的命题是真命题吗?为什么?
证明:等边对等角.
条件:
结论:
一个三角形的两条边相等;
它们所对的角也相等.
已知:如图,△ABC中,AB=AC,
求证∠B=∠C.
例 题 精 讲
D
C
A
B
在四边形ABCD中,有以下几个事项:
(1) AB∥CD
(2) ∠B=∠D
(3) AD∥BC
请用其中的两个事项作为条件,另一个事项作为结论,
构造一个命题.
你构造的命题是真命题吗?为什么?
例 题 精 讲
请用其中的三个事项作为已知条件,余下一个事项作为结论,构造一个命题.
你构造的命题是真命题吗?为什么?
A
D
F
C
B
E
如图,在△AFD 和△CEB中,点A,E,F,C在
同一直线上,下面有4个判断:
①AD=CB ②AE=FC
③ ∠ B= ∠ D ④AD ∥BC
例 题 精 讲
(1)如图(甲),在五角星图形中,
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。
A
E
A
B
C
D
E
(甲)
D
C
B
A
E
B
C
D
(乙)
(丙)
(2)把图(乙)、(丙)叫蜕化的五角星,问它们的五角之和与五角星图形的五角之和仍相等吗?为什么?
才 智 T 台
如图,在△ABC中,AB=AC,P是BC上的一点,PE ⊥ AB,
PF ⊥ AC, 垂足分别为E,F, BD是等腰三角形的腰AC上的高。
A
B
C
C
P
E
F
D
试探索BD, PF, PE三者关系
才 智 T 台
如图,在△ABC中,AB=AC, P是BC延长线上的一点,
PE ⊥ AB,PF ⊥ AC, 垂足分别为E,F, BD是等腰三角形的腰AC上的高。
试再探索BD , PE , PF 三者关系。
A
B
C
P
E
F
D
才 智 T 台
如图:在△ABC中,P是∠ B 、∠ C角平分线的交点,
∠BPC与∠A有怎样的大小关系?说说你的理由。
A
B
C
P
才 智 T 台
如图:在△ABC中,P是∠ B 、∠ C外角的角平分线的交点,
∠BPC与∠A有怎样的大小关系?说说你的理由。
A
B
C
P
拓展1
才 智 T 台
如图:在△ABC中,P是∠ B的角平分线 和
∠ C外角的角平分线的交点,
∠BPC与∠A有怎样的大小关系?说说你的理由。
拓展2
A
B
C
P
N
才 智 T 台
如图:在△ABC中,P是△ABC 内的任意一点,
∠BPC与∠A有怎样的大小关系?说说你的理由。
A
B
C
P
拓展3
才 智 T 台
拓展4
如图:在△ABC中,P,Q是∠ B 、∠ C三等分线的交点,
∠BPC与∠BQC 与∠ A有怎样的大小关系?
说说你的理由。
A
B
C
P
Q
才 智 T 台
已知,如图:AB ∥ CD
探索 ∠ E 与 ∠ B 、∠ D 的关系
A
B
C
D
E
①
②
A
B
C
D
E
③
A
B
C
D
E
④
A
B
C
D
E
才 智 T 台
本节课你学到什么?
收 获
1.下列句子中,不是命题的是( )
A.三角形的内角和等于180度; B.对顶角相等;
C.过一点作已知直线的垂线; D.两点确定一条直线.
2、三角形的三个内角中,锐角的个数不少于 ( )
A 1 个 B 2 个 C 3个 D 不确定
3、下列语句错误的是( )
A.同角的补角相等; B.同位角相等.
C.垂直于同一条直线的两直线平行; D.两条直线相交有且只有一个
4、以下命题中,真命题的是 ( )
A 两条线只有一个交点 B 同位角相等
C 两边和一角对应相等的两个三角形全等
D 等腰三角形底边中点到两腰相等
6、下面有3个判断:①一个三角形的3个内角中最多有1个直角;②一个三角形的3个内角中至少有两个锐角;③一个三角形的3个内角中至少有1个钝角.其中正确的有( ).
(A)0个 (B)1个 (C)2个 (D)3个
谢 谢
小结与思考
a
b
c
d
a
b
a
b
直观是把“双刃剑”
知识回顾
判断正误
观察.实验.操作
说理
证明
基本事实
定理
推论
真命题
假命题
原命题
逆命题
举反例
同位角相等,
两直线平行.
两直线平行,
同位角相等.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
三角形内角和等于180°
三角形的一个
外角等于和它
不相邻的两个
内角的和
三角形的一个
外角大于任何
一个和它不相
邻的内角
直角三角形
两锐角互余
命题
同位角相等,两直线平行.
两直线平行,同位角相等.
两边和它们的夹角对应相等的两个三角形全等.
两角和它们的夹边对应相等的两个三角形全等.
三边对应相等的两个三角形全等.
定义
学好几何的标志是会“证明”
证明命题的一般步骤:
根据命题,画出图形;
根据命题,结合图形,写出已知、求证;
写出证明过程.
注:运用数学符号和数学语言条理清晰地写出证明过程;
检查表达过程是否正确,完善。
知识回顾
对名称或术语的含义进行描述,做出规定,就是给出他们的定义.
“能够完全重合的图形”是“_______”的定义.
例如:
“符号不同、绝对值相等的两个数”是“ ”的定义;
互为相反数
全等形
无理数:
直角三角形:
无限不循环小数叫做无理数.
有一个角是直角的三角形叫做直角三角形.
知识回顾
正确的命题称为真命题,
不正确的的命题称为假命题.
命题:判断一件事情的句子,叫做命题.
命题由条件和结论两部分构成.
知识回顾
下面的句子哪些是命题
(1)每单位面积所受到的压力叫做压强;
(2)如果a是实数,那么a2+1〉0;
(3)两个无理数的乘积一定是无理数;
(4)偶数一定是合数吗?
(5)连接AB;
(6)不相等的两个角不可能是对顶角
练 一 练
对于命题“不相等的两个角不可能是对顶角”
条件:
结论:
改写成“如果……,那么……”的形式:
两个角不相等
这两个角不可能是对顶角
如果两个角不相等,那么这两个角不可能是对顶角
(3)两个无理数的乘积一定是无理数;
练 一 练
已知:如图6-13,在△ABC中,AD平分∠EAC, AD∥BC.
求证:∠B= ∠C.
1
2
例 题 精 讲
三角形内角和定理
例 题 精 讲
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
例 题 精 讲
如图. ∠1是△ABC的一个外角, ∠1与图中的其它角有什么关系
∠1+∠4=1800 ;
∠1=∠2+∠3;
∠1>∠ 2;
∠1>∠ 3.
A
B
C
D
1
2
3
4
例 题 精 讲
三角形内角和定理
已知:如图,已知AD是△ABD 和△ACD的公共边,求证:∠BDC=∠BAC+∠B+∠C
A
B
C
D
你还有其他方法解决这个问题吗
例 题 精 讲
你能把命题中的条件和结论互换, 构造一个新的命题吗
D
你构造的命题是真命题吗?为什么?
证明:等边对等角.
条件:
结论:
一个三角形的两条边相等;
它们所对的角也相等.
已知:如图,△ABC中,AB=AC,
求证∠B=∠C.
例 题 精 讲
D
C
A
B
在四边形ABCD中,有以下几个事项:
(1) AB∥CD
(2) ∠B=∠D
(3) AD∥BC
请用其中的两个事项作为条件,另一个事项作为结论,
构造一个命题.
你构造的命题是真命题吗?为什么?
例 题 精 讲
请用其中的三个事项作为已知条件,余下一个事项作为结论,构造一个命题.
你构造的命题是真命题吗?为什么?
A
D
F
C
B
E
如图,在△AFD 和△CEB中,点A,E,F,C在
同一直线上,下面有4个判断:
①AD=CB ②AE=FC
③ ∠ B= ∠ D ④AD ∥BC
例 题 精 讲
(1)如图(甲),在五角星图形中,
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。
A
E
A
B
C
D
E
(甲)
D
C
B
A
E
B
C
D
(乙)
(丙)
(2)把图(乙)、(丙)叫蜕化的五角星,问它们的五角之和与五角星图形的五角之和仍相等吗?为什么?
才 智 T 台
如图,在△ABC中,AB=AC,P是BC上的一点,PE ⊥ AB,
PF ⊥ AC, 垂足分别为E,F, BD是等腰三角形的腰AC上的高。
A
B
C
C
P
E
F
D
试探索BD, PF, PE三者关系
才 智 T 台
如图,在△ABC中,AB=AC, P是BC延长线上的一点,
PE ⊥ AB,PF ⊥ AC, 垂足分别为E,F, BD是等腰三角形的腰AC上的高。
试再探索BD , PE , PF 三者关系。
A
B
C
P
E
F
D
才 智 T 台
如图:在△ABC中,P是∠ B 、∠ C角平分线的交点,
∠BPC与∠A有怎样的大小关系?说说你的理由。
A
B
C
P
才 智 T 台
如图:在△ABC中,P是∠ B 、∠ C外角的角平分线的交点,
∠BPC与∠A有怎样的大小关系?说说你的理由。
A
B
C
P
拓展1
才 智 T 台
如图:在△ABC中,P是∠ B的角平分线 和
∠ C外角的角平分线的交点,
∠BPC与∠A有怎样的大小关系?说说你的理由。
拓展2
A
B
C
P
N
才 智 T 台
如图:在△ABC中,P是△ABC 内的任意一点,
∠BPC与∠A有怎样的大小关系?说说你的理由。
A
B
C
P
拓展3
才 智 T 台
拓展4
如图:在△ABC中,P,Q是∠ B 、∠ C三等分线的交点,
∠BPC与∠BQC 与∠ A有怎样的大小关系?
说说你的理由。
A
B
C
P
Q
才 智 T 台
已知,如图:AB ∥ CD
探索 ∠ E 与 ∠ B 、∠ D 的关系
A
B
C
D
E
①
②
A
B
C
D
E
③
A
B
C
D
E
④
A
B
C
D
E
才 智 T 台
本节课你学到什么?
收 获
1.下列句子中,不是命题的是( )
A.三角形的内角和等于180度; B.对顶角相等;
C.过一点作已知直线的垂线; D.两点确定一条直线.
2、三角形的三个内角中,锐角的个数不少于 ( )
A 1 个 B 2 个 C 3个 D 不确定
3、下列语句错误的是( )
A.同角的补角相等; B.同位角相等.
C.垂直于同一条直线的两直线平行; D.两条直线相交有且只有一个
4、以下命题中,真命题的是 ( )
A 两条线只有一个交点 B 同位角相等
C 两边和一角对应相等的两个三角形全等
D 等腰三角形底边中点到两腰相等
6、下面有3个判断:①一个三角形的3个内角中最多有1个直角;②一个三角形的3个内角中至少有两个锐角;③一个三角形的3个内角中至少有1个钝角.其中正确的有( ).
(A)0个 (B)1个 (C)2个 (D)3个
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
