【双减—同步分层作业】29.3课题学习 制作立体模型(含解析)
文档属性
| 名称 | 【双减—同步分层作业】29.3课题学习 制作立体模型(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 18:01:47 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【双减—同步分层作业】29.3课题学习 制作立体模型
一、知识梳理
1、如图,一个圆锥形橡皮泥的主视图是三角形ABC,若BC=6,则这个圆锥形橡皮泥的底面积为 .(不取近似值)
2、如图是一零件的三视图,则该零件的表面积为 .
二、夯实基础(必做题)
1.从某个方向观察一个正六棱柱,可看到如图所示的图形,其中四边形ABCD为矩形,E,F分别是AB,DC的中点.若AD=10cm,AB=6cm,则这个正六棱柱的侧面积为( )
A.360cm2 B.cm2 C.180cm2 D. cm2
2.如图所示是由八个完全相同的小正方体搭成的几何体从上面看到的形状图,小正方形中的数字表示该位置上小正方体的个数,则这个几何体从正面看到的形状图是( )
A. B. C. D.
3.用小正方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体最少需要正方体个数为a,最多需要正方体个数为b,则a+b的值为( )
A.14 B.15 C.16 D.17
4.如图2是图1长方体的三视图,若用S表示面积,S主视图=a2,S左视图=a2+a,则S俯视图=( )
A.2a2 B.2a2+a C.a2+a D.a2+2a+1
5.如图是一个几何体的三视图,根据图中提供的数据,计算这个几何体的表面积是( )
A.48+60π B.48+40π C.48+30π D.48+36π
6、用若干个相同的小正方体搭一个几何体,该几何体的主视图、俯视图如图所示.若小正方体的棱长为1,则搭成的几何体的表面积是 .
7、一个圆锥的主视图是边长为6cm的正三角形,则这个圆锥的侧面积等于 .
8、有一些大小相同的小正方体组成的简单几何体的主视图和俯视图(如图),若组成这个几何体的小正方体的块数为n,则n的所有可能值为 .
9、由若干相同大小的小正方体组成的几何体,从不同方向看到的图形如图所示,则组成该几何体最少需要 个小正方体,最多需要 个小正方体.
10、一个几何体是由若干个棱长为1的小正方体堆积而成的,从不同方向看到的几何体的形状图如下.
(1)在从上面看得到的形状图中标出相应位置小正方体的个数;
(2)这个几何体的表面积是 .
11、如图,是一个几何体分别从正面、左面、上面看的形状图.
(1)该几何体名称是 ;
(2)根据图中给的信息,求该几何体的表面积和体积.
12、一个几何体的三种视图如图所示.
(1)这个几何体的名称是 ,其侧面积为 ;
(2)画出它的一种表面展开图;
(3)求出左视图中AB的长.
13、如图是某几何体从正面、左面、上面看到的形状图.
(1)这个几何体的名称是 ;
(2)若从正面看到的长方形的宽为4cm,长为9cm,从左面看到的宽为3cm,从上面看到的直角三角形的斜边为5cm,则这个几何体中所有棱长的和是多少?它的表面积是多少.
三、能力提升(中等生加练题)
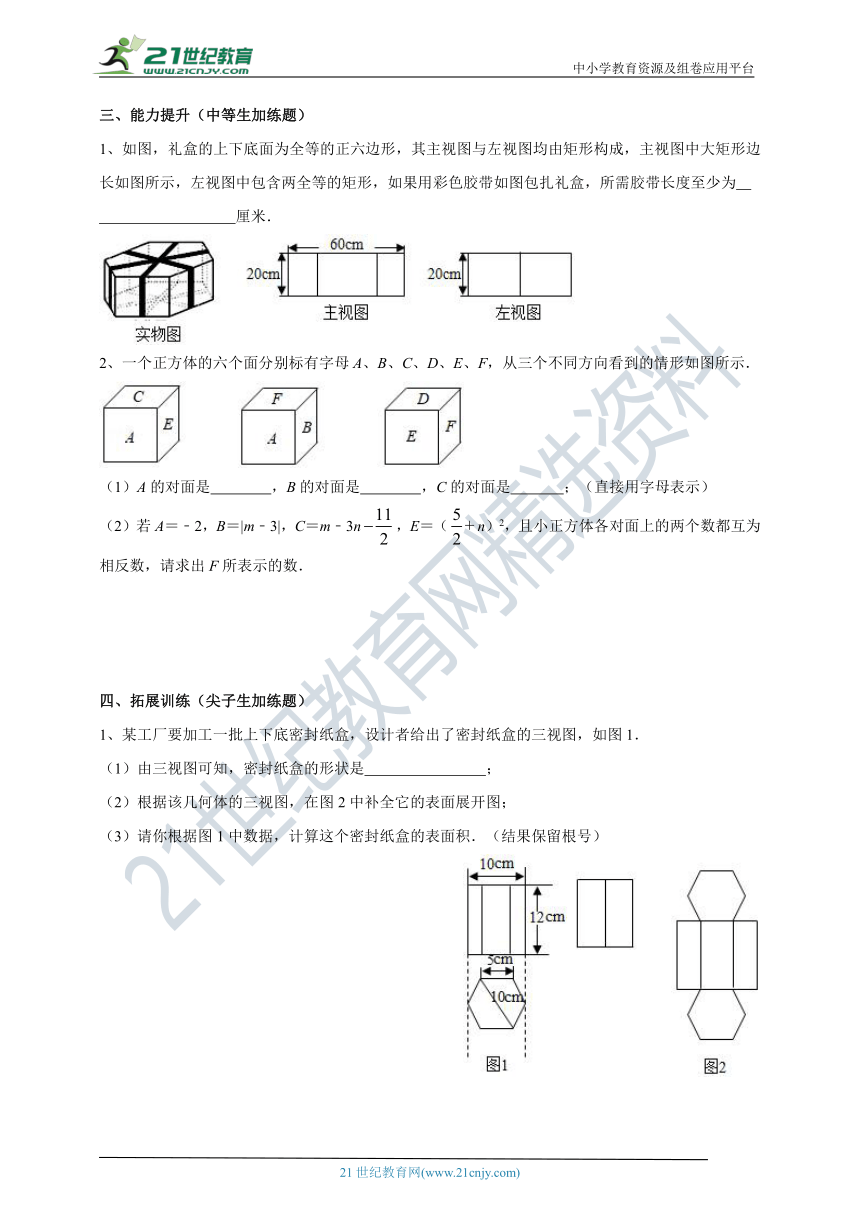
1、如图,礼盒的上下底面为全等的正六边形,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为
厘米.
2、一个正方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.
(1)A的对面是 ,B的对面是 ,C的对面是 ;(直接用字母表示)
(2)若A=﹣2,B=|m﹣3|,C=m﹣3n,E=(n)2,且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
四、拓展训练(尖子生加练题)
1、某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1.
(1)由三视图可知,密封纸盒的形状是 ;
(2)根据该几何体的三视图,在图2中补全它的表面展开图;
(3)请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)
2、双十一购物狂欢节,天猫“某玩具旗舰店”对乐高积木系列玩具将推出买一送一活动.根据积木数量的不同,厂家会订制不同型号的外包装盒.所有外包装盒均为双层上盖的长方体纸箱(上盖纸板面积刚好等于底面面积的2倍,如图1).长方体纸箱的长为a厘米,宽为b厘米,高为c厘米.
(1)请用含有a,b,c的代数式表示制作长方体纸箱需要 平方厘米纸板;
(2)如图2为若干包装好的同一型号玩具堆成几何体的三视图,则组成这个几何体的玩具个数最少为 个;
(3)由于旗舰店在双十一期间推出买一送一的活动,现要将两个同一型号的乐高积木包装在同一个大长方体的外包装盒内,已知单个乐高积木的长方体纸盒长和高相等,且宽小于长.如图3所示,现有甲,乙两种摆放方式,请分别计算甲,乙两种摆放方式所需外包装盒的纸板面积(包装盒上盖朝上),并比较哪一种方式所需纸板面积更少,说明理由.
【参考答案】
一、
1、9π 解:由题意,底面圆的直径为6,
∴底面积=π×32=9π,
故答案为:9π.
2、36πcm 解:由三视图知,该几何体是底面半径为4cm、高为4cm的圆锥体,
则该圆锥的母线长为
∴该零件的表面积为=16π+20π=36π(cm2),
故答案为:36πcm
二、
1、B 解:如图,正六边形的边长为AG、BG,
GE垂直平分AB,
由正六边形的性质可知,∠AGB=120°,∠A=∠B=30°,AEAB=3,
所以,
正六棱柱的侧面积=6AG×AD=
故选:B.
2、B 解:从正面看易得共由3列,从左到右小正方形的个数分别为:3、2、2.
故选:B.
3、C 解:由俯视图可得最底层有5个小正方体,
由主视图可得第一列和第三列最少有2个正方体,最多有4个正方体,
那么最少需要5+2=7个正方体,即a=7.
最多需要5+4=9个正方体,即b=9.
则a+b=7+9=16.
故选:C.
4、C 解:∵S主视图=a2=a a,S左视图=a2+a=a(a+1),
∴俯视图的长为a+1,宽为a,
∴S俯视图=a (a+1)=a2+a,
故选:C.
5、A 解:由三视图知,该几何体是底面半径为4、高为6的圆柱被沿高的方向切掉一个圆的几何体,
所以其表面积为2π×4×6+2×4×6+2π×42=36π+48+24π=60π+48,
故选:A.
6、28或30 解:搭这样的几何体最少需要4+1+2=7个小正方体,最多需要4+2+2=8个小正方体,
所以搭成的几何体的表面积是4×7=28或4×8﹣2=30,
故答案为:28或30.
7、18πcm2 解:根据题意得圆锥的母线长为6cm,底面圆的半径为3cm,
所以这个圆锥的侧面积6×2π×3=18π(cm2)
故答案为:18πcm2.
8、8,9,10,11 解:主视图最右边可能有4或5或6个小正方体;
由主视图最左边看到只有一列,俯视图也只有一列,则左边有一个小正方体;
主视图中间有两列,俯视图亦有两列,则中间可以有3或4个小正方形.
∴n的值可能为:1+4+3=8,1+5+3=9,1+6+3=10,1+4+4=9,1+5+4=10,1+6+4=11,
故本题答案为:8,9,10,11.
9、8,10 解:最多有:3+2+2+2+1=10(个),最少有:3+2+1+1+1=8(个).
故答案为:8,10.
10、解:(1)如图所示:
(2)这个几何体的表面积为2×(6+4+5)=30,
故答案为:30
11、解:(1)这个几何体是四棱柱,
故答案为:四棱柱;
(2)这个四棱柱的表面积=2×(10×5+5×6+10×6)=280(cm2).
体积=10×5×6=300(cm3)
12、解:(1)这个几何体的名称是正三棱柱,
这个几何体的侧面积为4×3×6=72.
故答案为:正三棱柱,72;
(2)展开图如下:
(3)在△EFG中,作EH⊥FG于点H,
则
故左视图中AB的长为
13、解:(1)这个几何体是三棱柱.
故答案为:三棱柱.
(2)这个几何体的所有棱长的和=9×3+2×(3+4+5)=51(cm).
表面积=23×4+9×(3+4+5)=120(cm2)
三、
1、解:根据题意,作出实际图形的上底,
如图:AC,CD是上底面的两边.
则AC=60÷2=30(cm),∠ACD=120°,
作CB⊥AD于点B,
那么AB=AC×sin60°=15(cm),
所以AD=2AB=30(cm),
胶带的长至少=306+20×6=(180+120)(cm).
故答案为:(180+120).
2、解:(1)由图可得,A与B、C、E、F都相邻,故A对面的字母是D;
E与A、C、D、F都相邻,故B对面的字母是E;
故C的对面是F.
故答案为:D,E,F;
(2)∵字母B表示的数与它对面的字母E表示的数互为相反数,
∴|m﹣3|+(n)2=0,
∴m﹣3=0,n=0,
解得m=3,n=
∴C=m﹣3n3﹣3×()5,
∴F所表示的数是﹣5.
四、
1、解:(1)根据该几何体的三视图知道它是一个正六棱柱.
故答案为:正六棱柱;
(2)六棱柱的表面展开图如图2:(本题只给出一种图形,其它图形请参考给分);
(3)由图中数据可知:六棱柱的高为12cm,底面边长为5cm,
∴六棱柱的侧面积为6×5×12=360(cm2).
又∵密封纸盒的底面面积为:
∴六棱柱的表面积为(75+360)cm2.
2、解:(1)制作长方体纸箱需要(2ac+2bc+3ab)平方厘米纸板;
故答案为:(2ac+2bc+3ab);
(2)根据三视图知,则组成这个几何体的玩具个数最少的分布情况如下图所示:
所以组成这个几何体的玩具个数最少为9个,
故答案为:9;
(3)如图3,由题意得:a=c,a>b,
甲:2(ac+2bc+2ab)+2ab,
乙:2(2ab+2ac+bc)+2ab,
∵a>b,
∴ac>bc,
∴ac﹣bc>0,
∵甲所需纸板面积﹣乙所需纸板面积=2(ac+2bc﹣2ac﹣bc)=2(bc﹣ac)<0,
∴甲种摆放方式所需外包装盒的纸板面积更少.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【双减—同步分层作业】29.3课题学习 制作立体模型
一、知识梳理
1、如图,一个圆锥形橡皮泥的主视图是三角形ABC,若BC=6,则这个圆锥形橡皮泥的底面积为 .(不取近似值)
2、如图是一零件的三视图,则该零件的表面积为 .
二、夯实基础(必做题)
1.从某个方向观察一个正六棱柱,可看到如图所示的图形,其中四边形ABCD为矩形,E,F分别是AB,DC的中点.若AD=10cm,AB=6cm,则这个正六棱柱的侧面积为( )
A.360cm2 B.cm2 C.180cm2 D. cm2
2.如图所示是由八个完全相同的小正方体搭成的几何体从上面看到的形状图,小正方形中的数字表示该位置上小正方体的个数,则这个几何体从正面看到的形状图是( )
A. B. C. D.
3.用小正方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体最少需要正方体个数为a,最多需要正方体个数为b,则a+b的值为( )
A.14 B.15 C.16 D.17
4.如图2是图1长方体的三视图,若用S表示面积,S主视图=a2,S左视图=a2+a,则S俯视图=( )
A.2a2 B.2a2+a C.a2+a D.a2+2a+1
5.如图是一个几何体的三视图,根据图中提供的数据,计算这个几何体的表面积是( )
A.48+60π B.48+40π C.48+30π D.48+36π
6、用若干个相同的小正方体搭一个几何体,该几何体的主视图、俯视图如图所示.若小正方体的棱长为1,则搭成的几何体的表面积是 .
7、一个圆锥的主视图是边长为6cm的正三角形,则这个圆锥的侧面积等于 .
8、有一些大小相同的小正方体组成的简单几何体的主视图和俯视图(如图),若组成这个几何体的小正方体的块数为n,则n的所有可能值为 .
9、由若干相同大小的小正方体组成的几何体,从不同方向看到的图形如图所示,则组成该几何体最少需要 个小正方体,最多需要 个小正方体.
10、一个几何体是由若干个棱长为1的小正方体堆积而成的,从不同方向看到的几何体的形状图如下.
(1)在从上面看得到的形状图中标出相应位置小正方体的个数;
(2)这个几何体的表面积是 .
11、如图,是一个几何体分别从正面、左面、上面看的形状图.
(1)该几何体名称是 ;
(2)根据图中给的信息,求该几何体的表面积和体积.
12、一个几何体的三种视图如图所示.
(1)这个几何体的名称是 ,其侧面积为 ;
(2)画出它的一种表面展开图;
(3)求出左视图中AB的长.
13、如图是某几何体从正面、左面、上面看到的形状图.
(1)这个几何体的名称是 ;
(2)若从正面看到的长方形的宽为4cm,长为9cm,从左面看到的宽为3cm,从上面看到的直角三角形的斜边为5cm,则这个几何体中所有棱长的和是多少?它的表面积是多少.
三、能力提升(中等生加练题)
1、如图,礼盒的上下底面为全等的正六边形,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为
厘米.
2、一个正方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.
(1)A的对面是 ,B的对面是 ,C的对面是 ;(直接用字母表示)
(2)若A=﹣2,B=|m﹣3|,C=m﹣3n,E=(n)2,且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
四、拓展训练(尖子生加练题)
1、某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1.
(1)由三视图可知,密封纸盒的形状是 ;
(2)根据该几何体的三视图,在图2中补全它的表面展开图;
(3)请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)
2、双十一购物狂欢节,天猫“某玩具旗舰店”对乐高积木系列玩具将推出买一送一活动.根据积木数量的不同,厂家会订制不同型号的外包装盒.所有外包装盒均为双层上盖的长方体纸箱(上盖纸板面积刚好等于底面面积的2倍,如图1).长方体纸箱的长为a厘米,宽为b厘米,高为c厘米.
(1)请用含有a,b,c的代数式表示制作长方体纸箱需要 平方厘米纸板;
(2)如图2为若干包装好的同一型号玩具堆成几何体的三视图,则组成这个几何体的玩具个数最少为 个;
(3)由于旗舰店在双十一期间推出买一送一的活动,现要将两个同一型号的乐高积木包装在同一个大长方体的外包装盒内,已知单个乐高积木的长方体纸盒长和高相等,且宽小于长.如图3所示,现有甲,乙两种摆放方式,请分别计算甲,乙两种摆放方式所需外包装盒的纸板面积(包装盒上盖朝上),并比较哪一种方式所需纸板面积更少,说明理由.
【参考答案】
一、
1、9π 解:由题意,底面圆的直径为6,
∴底面积=π×32=9π,
故答案为:9π.
2、36πcm 解:由三视图知,该几何体是底面半径为4cm、高为4cm的圆锥体,
则该圆锥的母线长为
∴该零件的表面积为=16π+20π=36π(cm2),
故答案为:36πcm
二、
1、B 解:如图,正六边形的边长为AG、BG,
GE垂直平分AB,
由正六边形的性质可知,∠AGB=120°,∠A=∠B=30°,AEAB=3,
所以,
正六棱柱的侧面积=6AG×AD=
故选:B.
2、B 解:从正面看易得共由3列,从左到右小正方形的个数分别为:3、2、2.
故选:B.
3、C 解:由俯视图可得最底层有5个小正方体,
由主视图可得第一列和第三列最少有2个正方体,最多有4个正方体,
那么最少需要5+2=7个正方体,即a=7.
最多需要5+4=9个正方体,即b=9.
则a+b=7+9=16.
故选:C.
4、C 解:∵S主视图=a2=a a,S左视图=a2+a=a(a+1),
∴俯视图的长为a+1,宽为a,
∴S俯视图=a (a+1)=a2+a,
故选:C.
5、A 解:由三视图知,该几何体是底面半径为4、高为6的圆柱被沿高的方向切掉一个圆的几何体,
所以其表面积为2π×4×6+2×4×6+2π×42=36π+48+24π=60π+48,
故选:A.
6、28或30 解:搭这样的几何体最少需要4+1+2=7个小正方体,最多需要4+2+2=8个小正方体,
所以搭成的几何体的表面积是4×7=28或4×8﹣2=30,
故答案为:28或30.
7、18πcm2 解:根据题意得圆锥的母线长为6cm,底面圆的半径为3cm,
所以这个圆锥的侧面积6×2π×3=18π(cm2)
故答案为:18πcm2.
8、8,9,10,11 解:主视图最右边可能有4或5或6个小正方体;
由主视图最左边看到只有一列,俯视图也只有一列,则左边有一个小正方体;
主视图中间有两列,俯视图亦有两列,则中间可以有3或4个小正方形.
∴n的值可能为:1+4+3=8,1+5+3=9,1+6+3=10,1+4+4=9,1+5+4=10,1+6+4=11,
故本题答案为:8,9,10,11.
9、8,10 解:最多有:3+2+2+2+1=10(个),最少有:3+2+1+1+1=8(个).
故答案为:8,10.
10、解:(1)如图所示:
(2)这个几何体的表面积为2×(6+4+5)=30,
故答案为:30
11、解:(1)这个几何体是四棱柱,
故答案为:四棱柱;
(2)这个四棱柱的表面积=2×(10×5+5×6+10×6)=280(cm2).
体积=10×5×6=300(cm3)
12、解:(1)这个几何体的名称是正三棱柱,
这个几何体的侧面积为4×3×6=72.
故答案为:正三棱柱,72;
(2)展开图如下:
(3)在△EFG中,作EH⊥FG于点H,
则
故左视图中AB的长为
13、解:(1)这个几何体是三棱柱.
故答案为:三棱柱.
(2)这个几何体的所有棱长的和=9×3+2×(3+4+5)=51(cm).
表面积=23×4+9×(3+4+5)=120(cm2)
三、
1、解:根据题意,作出实际图形的上底,
如图:AC,CD是上底面的两边.
则AC=60÷2=30(cm),∠ACD=120°,
作CB⊥AD于点B,
那么AB=AC×sin60°=15(cm),
所以AD=2AB=30(cm),
胶带的长至少=306+20×6=(180+120)(cm).
故答案为:(180+120).
2、解:(1)由图可得,A与B、C、E、F都相邻,故A对面的字母是D;
E与A、C、D、F都相邻,故B对面的字母是E;
故C的对面是F.
故答案为:D,E,F;
(2)∵字母B表示的数与它对面的字母E表示的数互为相反数,
∴|m﹣3|+(n)2=0,
∴m﹣3=0,n=0,
解得m=3,n=
∴C=m﹣3n3﹣3×()5,
∴F所表示的数是﹣5.
四、
1、解:(1)根据该几何体的三视图知道它是一个正六棱柱.
故答案为:正六棱柱;
(2)六棱柱的表面展开图如图2:(本题只给出一种图形,其它图形请参考给分);
(3)由图中数据可知:六棱柱的高为12cm,底面边长为5cm,
∴六棱柱的侧面积为6×5×12=360(cm2).
又∵密封纸盒的底面面积为:
∴六棱柱的表面积为(75+360)cm2.
2、解:(1)制作长方体纸箱需要(2ac+2bc+3ab)平方厘米纸板;
故答案为:(2ac+2bc+3ab);
(2)根据三视图知,则组成这个几何体的玩具个数最少的分布情况如下图所示:
所以组成这个几何体的玩具个数最少为9个,
故答案为:9;
(3)如图3,由题意得:a=c,a>b,
甲:2(ac+2bc+2ab)+2ab,
乙:2(2ab+2ac+bc)+2ab,
∵a>b,
∴ac>bc,
∴ac﹣bc>0,
∵甲所需纸板面积﹣乙所需纸板面积=2(ac+2bc﹣2ac﹣bc)=2(bc﹣ac)<0,
∴甲种摆放方式所需外包装盒的纸板面积更少.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
