2021-2022学年苏科版九年级数学下册6.3相似图形巩固训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册6.3相似图形巩固训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 198.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 18:23:27 | ||
图片预览



文档简介
6.3相似图形
一、选择题
1、下列四组图形中,一定相似的是( )
A.正方形与矩形 B.正方形与菱形 C.菱形与菱形 D.正五边形与正五边形
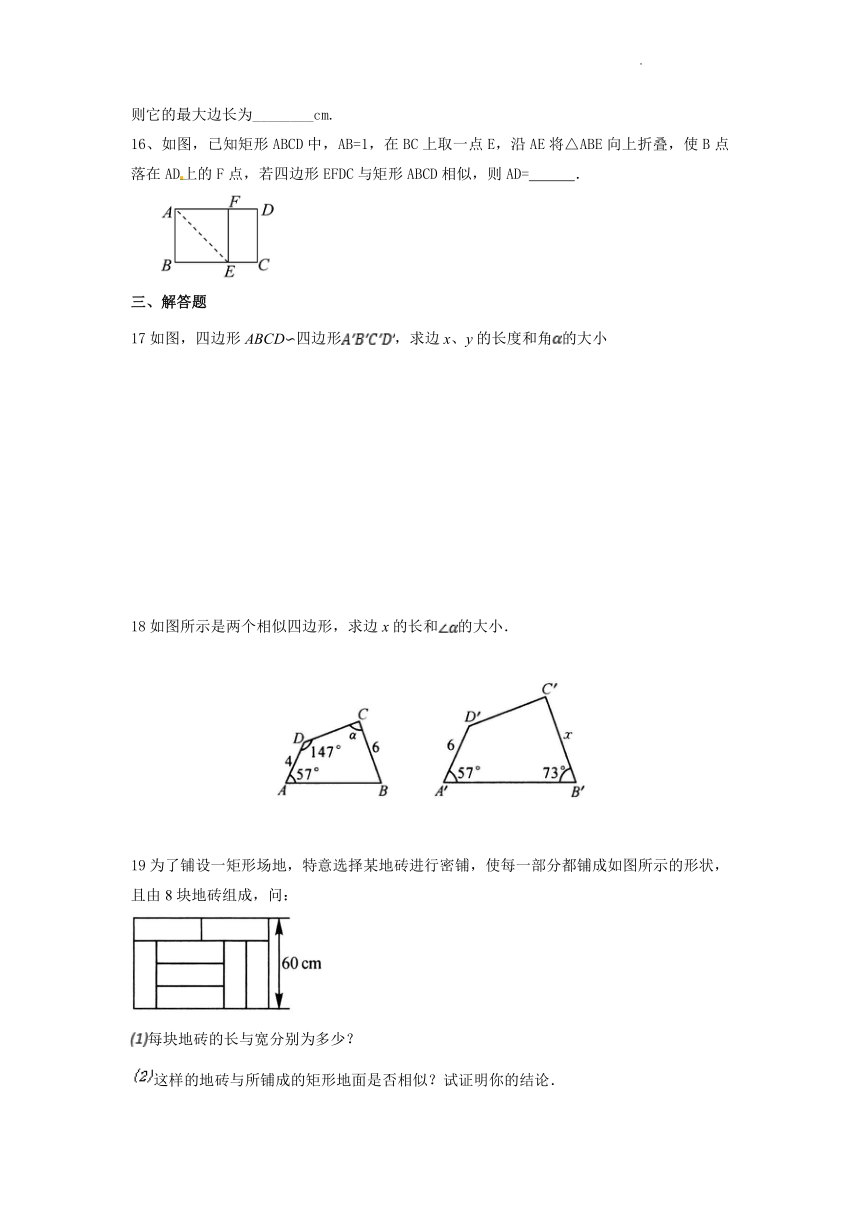
2、下列各组图形相似的是( )
3、下列说法:①放大(或缩小)的图片与原图片是相似图形;②比例尺不同的中国地图是相似图形;
③放电影时胶片上的图象和它映射到屏幕上的图象是相似图形;
④平面镜中,你的形象与你本人是相似的. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4、如图,已知△ABC∽△ADE,且∠ADE=∠B,则下列比例式成立的是( )
A. = B. = C. = D. =
5、已知A4纸的宽度为21 cm,如图对折后所得的两个矩形都和原来的矩形相似,则A4纸的高度约为( )
A.24.8 cm B.26.7 cm C.29.7 cm D.无法确定
6、两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为( )
A. B. C. D.
7、下列3个矩形中,相似的是( )
①长为8cm,宽为6cm;②长为8cm,宽为4cm;③长为6cm,宽为4.5cm
A.①②和③ B.①和② C.①和③ D.②和③
8如图,在长为、宽为的矩形中,截去一个矩形,使得留下的矩形图中阴影部分与原矩形相似,则留下的矩形面积是
A. B. C. D.
9下列说法:有一个锐角相等的两个直角三角形相似;顶角相等的两个等腰三角形相似;任意两个菱形一定相似;位似图形一定是相似图形;其中正确的个数是
A. 1个 B. 2个 C. 3个 D. 4个
10两个五角星相似,相似比为,则它们的面积比等于
A. B. C. D.
二、填空题
11.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是________ cm2 .
12. 用同一张底片洗出的两张照片,一张为寸,另一张为寸,则这两张照片上的图象的相似比是________.
13. 下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图象是相似的图形;②用彩笔在黑板上写上三个大字,,,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是________,错误的是________.(填序号)
14. 一匹骏马在草原上奔跑,摄影师在某处随机拍下几张照片,这些照片中的骏马形状应该是________的.(填“相同”或“不同”)
15、如图,在长8 cm、宽4 cm的矩形中截去一个矩形(阴影部分),使留下的矩形与原矩形相似,那么留下的矩形的宽为_______cm.
15、一个四边形的各边长之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为5 cm,
则它的最大边长为________cm.
16、如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= .
三、解答题
17如图,四边形ABCD∽四边形,求边x、y的长度和角的大小
18如图所示是两个相似四边形,求边x的长和的大小.
19为了铺设一矩形场地,特意选择某地砖进行密铺,使每一部分都铺成如图所示的形状,且由8块地砖组成,问:
每块地砖的长与宽分别为多少?
这样的地砖与所铺成的矩形地面是否相似?试证明你的结论.
20、为方便居民活动,某小区计划在AD=10 m,AB=30 m的矩形花坛四周修筑小路.
(1)如果四周的小路的宽均相等,都是x,如图1,那么小路四周所围成的矩形A'B'C'D'和矩形ABCD相似吗 请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为x,y,如图2,试问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形A'B'C'D'和矩形ABCD相似 请说明理由.
21.图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列),∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°.
(1)求∠F的度数;
(2)如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,求C1D1的长度.
22.如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
(答案)
一、选择题
1、D 2、B 3、D 4、B 5、C 6、A 7、C 8、A 9、D 10、C
二、填空题
11. 18
12.【答案 1:3
13.【答案】①,②③
14.【答案】不同
15、2
16、
三、解答题
17.【答案】解:
四边形ABCD∽四边形,
,,
,,
.
19.【答案】解:设矩形地砖的长为a cm,宽为b cm,
由图可知,即.
因为,
所以.
所以矩形地砖的长为,宽为;
不相似.
证明:因为所铺成矩形地面的长为,宽为,
所以.
因为,,
即所铺成的矩形地面的长与宽和地砖的长与宽不成比例,
所以它们不相似.
17、如图的相似四边形中,求未知边x,y的长度和∠α的大小.
答案:x=31.5,y=27,∠α=83°
18、如图,六边形ABCDEF与六边形A′B′C′D′E′F′相似.
求:(1)相似比;
(2)∠A和∠B′的度数;
(3)边CD,EF,A′F′,E′D′的长.
解:(1)∵六边形ABCDEF与六边形A′B′C′D′E′F′相似,BC与B′C′是对应边,
∴=,即相似比为.
(2)∵六边形ABCDEF与六边形A′B′C′D′E′F′相似,∴∠A=∠A′,∠B=∠B′.
又∵∠A′=90°,∠B=150°,∴∠A=90°,∠B′=150°.
(3)∵六边形ABCDEF与六边形A′B′C′D′E′F′相似,
∴====.由=,AF=4 cm,
得=, ∴A′F′=(cm).
由=,E′F′=4 cm,得=, ∴EF=(cm).
由=,ED=5 cm,得=, ∴E′D′=(cm).
由=,C′D′=3 cm,得=, ∴CD=(cm).
即CD= cm,EF= cm, A′F′= cm, E′D′= cm.
19、一个矩形ABCD的较短边长为2.
(1) 如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2) 如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
解:(1)由已知得MN=AB=2,MD=AD=BC,
∵沿长边对折后得到的矩形与原矩形相似,∴矩形DMNC与矩形ABCD相似,,
∴DM BC=AB MN,即BC2=4,∴BC=,即它的另一边长为;
∵矩形EFDC与原矩形ABCD相似,∴=,
∵AB=CD=2,BC=4,∴DF==1,∴矩形EFDC的面积=CD DF=2×1=2.
20、为方便居民活动,某小区计划在AD=10 m,AB=30 m的矩形花坛四周修筑小路.
(1)如果四周的小路的宽均相等,都是x,如图1,那么小路四周所围成的矩形A'B'C'D'和矩形ABCD相似吗 请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为x,y,如图2,试问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形A'B'C'D'和矩形ABCD相似 请说明理由.
解:(1)不相似,理由:
因为≠,所以矩形A'B'C'D'和矩形ABCD不相似.
(2)当矩形A'B'C'D'和矩形ABCD相似时,
则有=,解得=, 即当=时,矩形A'B'C'D'和矩形ABCD相似.
21【答案】 (1)解:∵多边形ABCDEF和A1B1C1D1E1F1相似,∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°,∴∠C=∠C1=95°,∠D=∠D1=135°,∠E=∠E1=120°.
由多边形内角和定理,得多边形ABCDEF的内角和为180°×(6-2)=720°,
∴∠F=720°-(135°+120°+95°+135°+120°)=115°
(2)解:∵多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,
∴C1D1=15×1.5=22.5(cm).
22【答案】 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠FAE=∠AEB,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴ ,即 ,
解得:BC=3±3 (负值舍去),
∴BC=3+3
一、选择题
1、下列四组图形中,一定相似的是( )
A.正方形与矩形 B.正方形与菱形 C.菱形与菱形 D.正五边形与正五边形
2、下列各组图形相似的是( )
3、下列说法:①放大(或缩小)的图片与原图片是相似图形;②比例尺不同的中国地图是相似图形;
③放电影时胶片上的图象和它映射到屏幕上的图象是相似图形;
④平面镜中,你的形象与你本人是相似的. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4、如图,已知△ABC∽△ADE,且∠ADE=∠B,则下列比例式成立的是( )
A. = B. = C. = D. =
5、已知A4纸的宽度为21 cm,如图对折后所得的两个矩形都和原来的矩形相似,则A4纸的高度约为( )
A.24.8 cm B.26.7 cm C.29.7 cm D.无法确定
6、两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为( )
A. B. C. D.
7、下列3个矩形中,相似的是( )
①长为8cm,宽为6cm;②长为8cm,宽为4cm;③长为6cm,宽为4.5cm
A.①②和③ B.①和② C.①和③ D.②和③
8如图,在长为、宽为的矩形中,截去一个矩形,使得留下的矩形图中阴影部分与原矩形相似,则留下的矩形面积是
A. B. C. D.
9下列说法:有一个锐角相等的两个直角三角形相似;顶角相等的两个等腰三角形相似;任意两个菱形一定相似;位似图形一定是相似图形;其中正确的个数是
A. 1个 B. 2个 C. 3个 D. 4个
10两个五角星相似,相似比为,则它们的面积比等于
A. B. C. D.
二、填空题
11.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是________ cm2 .
12. 用同一张底片洗出的两张照片,一张为寸,另一张为寸,则这两张照片上的图象的相似比是________.
13. 下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图象是相似的图形;②用彩笔在黑板上写上三个大字,,,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是________,错误的是________.(填序号)
14. 一匹骏马在草原上奔跑,摄影师在某处随机拍下几张照片,这些照片中的骏马形状应该是________的.(填“相同”或“不同”)
15、如图,在长8 cm、宽4 cm的矩形中截去一个矩形(阴影部分),使留下的矩形与原矩形相似,那么留下的矩形的宽为_______cm.
15、一个四边形的各边长之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为5 cm,
则它的最大边长为________cm.
16、如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= .
三、解答题
17如图,四边形ABCD∽四边形,求边x、y的长度和角的大小
18如图所示是两个相似四边形,求边x的长和的大小.
19为了铺设一矩形场地,特意选择某地砖进行密铺,使每一部分都铺成如图所示的形状,且由8块地砖组成,问:
每块地砖的长与宽分别为多少?
这样的地砖与所铺成的矩形地面是否相似?试证明你的结论.
20、为方便居民活动,某小区计划在AD=10 m,AB=30 m的矩形花坛四周修筑小路.
(1)如果四周的小路的宽均相等,都是x,如图1,那么小路四周所围成的矩形A'B'C'D'和矩形ABCD相似吗 请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为x,y,如图2,试问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形A'B'C'D'和矩形ABCD相似 请说明理由.
21.图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列),∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°.
(1)求∠F的度数;
(2)如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,求C1D1的长度.
22.如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
(答案)
一、选择题
1、D 2、B 3、D 4、B 5、C 6、A 7、C 8、A 9、D 10、C
二、填空题
11. 18
12.【答案 1:3
13.【答案】①,②③
14.【答案】不同
15、2
16、
三、解答题
17.【答案】解:
四边形ABCD∽四边形,
,,
,,
.
19.【答案】解:设矩形地砖的长为a cm,宽为b cm,
由图可知,即.
因为,
所以.
所以矩形地砖的长为,宽为;
不相似.
证明:因为所铺成矩形地面的长为,宽为,
所以.
因为,,
即所铺成的矩形地面的长与宽和地砖的长与宽不成比例,
所以它们不相似.
17、如图的相似四边形中,求未知边x,y的长度和∠α的大小.
答案:x=31.5,y=27,∠α=83°
18、如图,六边形ABCDEF与六边形A′B′C′D′E′F′相似.
求:(1)相似比;
(2)∠A和∠B′的度数;
(3)边CD,EF,A′F′,E′D′的长.
解:(1)∵六边形ABCDEF与六边形A′B′C′D′E′F′相似,BC与B′C′是对应边,
∴=,即相似比为.
(2)∵六边形ABCDEF与六边形A′B′C′D′E′F′相似,∴∠A=∠A′,∠B=∠B′.
又∵∠A′=90°,∠B=150°,∴∠A=90°,∠B′=150°.
(3)∵六边形ABCDEF与六边形A′B′C′D′E′F′相似,
∴====.由=,AF=4 cm,
得=, ∴A′F′=(cm).
由=,E′F′=4 cm,得=, ∴EF=(cm).
由=,ED=5 cm,得=, ∴E′D′=(cm).
由=,C′D′=3 cm,得=, ∴CD=(cm).
即CD= cm,EF= cm, A′F′= cm, E′D′= cm.
19、一个矩形ABCD的较短边长为2.
(1) 如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2) 如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
解:(1)由已知得MN=AB=2,MD=AD=BC,
∵沿长边对折后得到的矩形与原矩形相似,∴矩形DMNC与矩形ABCD相似,,
∴DM BC=AB MN,即BC2=4,∴BC=,即它的另一边长为;
∵矩形EFDC与原矩形ABCD相似,∴=,
∵AB=CD=2,BC=4,∴DF==1,∴矩形EFDC的面积=CD DF=2×1=2.
20、为方便居民活动,某小区计划在AD=10 m,AB=30 m的矩形花坛四周修筑小路.
(1)如果四周的小路的宽均相等,都是x,如图1,那么小路四周所围成的矩形A'B'C'D'和矩形ABCD相似吗 请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为x,y,如图2,试问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形A'B'C'D'和矩形ABCD相似 请说明理由.
解:(1)不相似,理由:
因为≠,所以矩形A'B'C'D'和矩形ABCD不相似.
(2)当矩形A'B'C'D'和矩形ABCD相似时,
则有=,解得=, 即当=时,矩形A'B'C'D'和矩形ABCD相似.
21【答案】 (1)解:∵多边形ABCDEF和A1B1C1D1E1F1相似,∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°,∴∠C=∠C1=95°,∠D=∠D1=135°,∠E=∠E1=120°.
由多边形内角和定理,得多边形ABCDEF的内角和为180°×(6-2)=720°,
∴∠F=720°-(135°+120°+95°+135°+120°)=115°
(2)解:∵多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,
∴C1D1=15×1.5=22.5(cm).
22【答案】 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠FAE=∠AEB,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴ ,即 ,
解得:BC=3±3 (负值舍去),
∴BC=3+3
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
