2021-2022学年人教版数学七年级下册5.1.1相交线同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册5.1.1相交线同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 393.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 18:23:31 | ||
图片预览

文档简介
2021-2022学年七年级下册数学巩固练习(人教版)
5.1.1相交线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在同一平面内,不重合的两条直线的位置关系可能是( )
A.相交或平行 B.相交 C.平行 D.不能确定
2.下列图形中,与是对顶角的是( )
A. B. C. D.
3.下列各图中,与互为邻补角的是( )
A. B.
C. D.
4.下列说法正确的是( )
A.大小相等的两个角互为对顶角
B.有公共顶点且相等的两个角是对顶角
C.两角之和为180°,则这两个角互为邻补角
D.—个角的邻补角可能是锐角、钝角或直角
5.如图,直线a、b相交于点O,若等于50°,则等于( )
A.50° B.40° C.140° D.130°
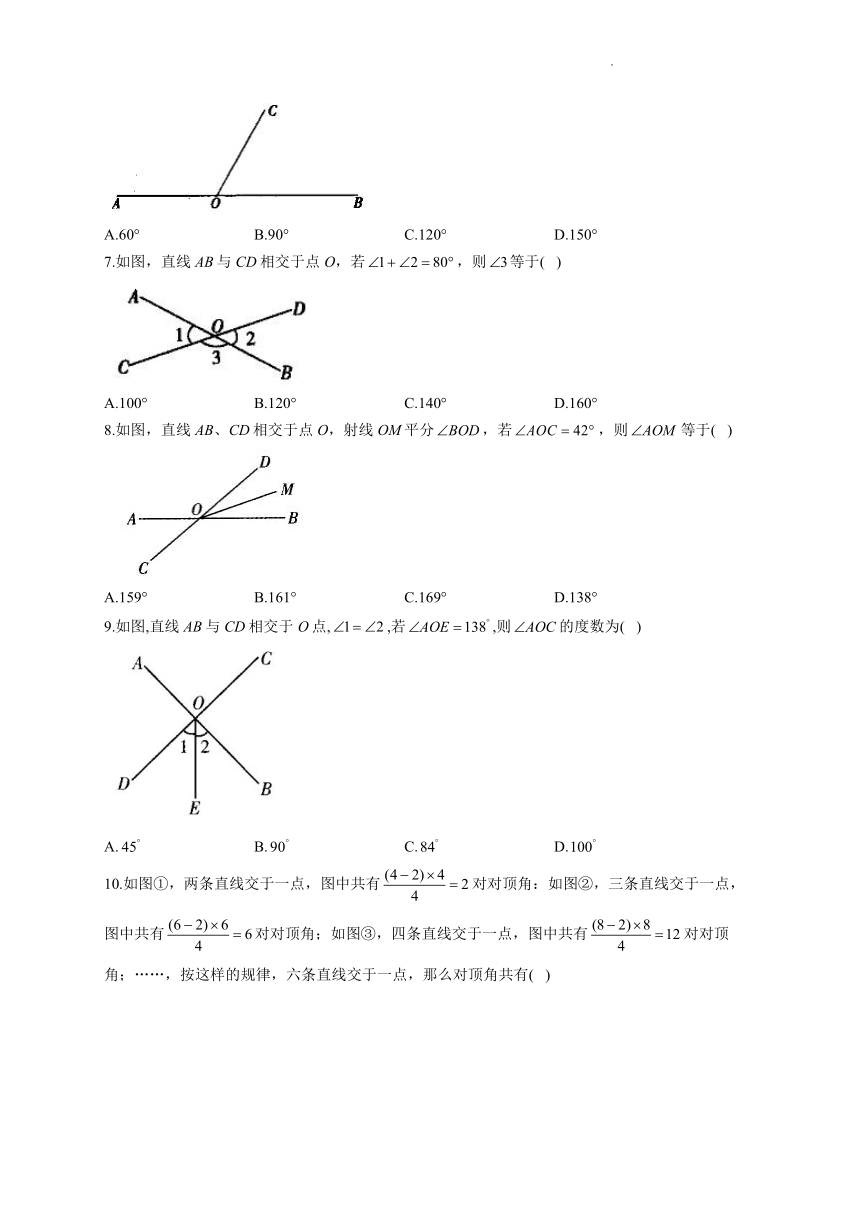
6.如图,点O在直线AB上,若,则的大小是( )
A.60° B.90° C.120° D.150°
7.如图,直线AB与CD相交于点O,若,则等于( )
A.100° B.120° C.140° D.160°
8.如图,直线AB、CD相交于点O,射线OM平分,若,则等于( )
A.159° B.161° C.169° D.138°
9.如图,直线AB与CD相交于O点,,若,则的度数为( )
A. B. C. D.
10.如图①,两条直线交于一点,图中共有对对顶角:如图②,三条直线交于一点,图中共有对对顶角;如图③,四条直线交于一点,图中共有对对顶角;……,按这样的规律,六条直线交于一点,那么对顶角共有( )
A.28对 B.30对 C.40对 D.60对
三、填空题
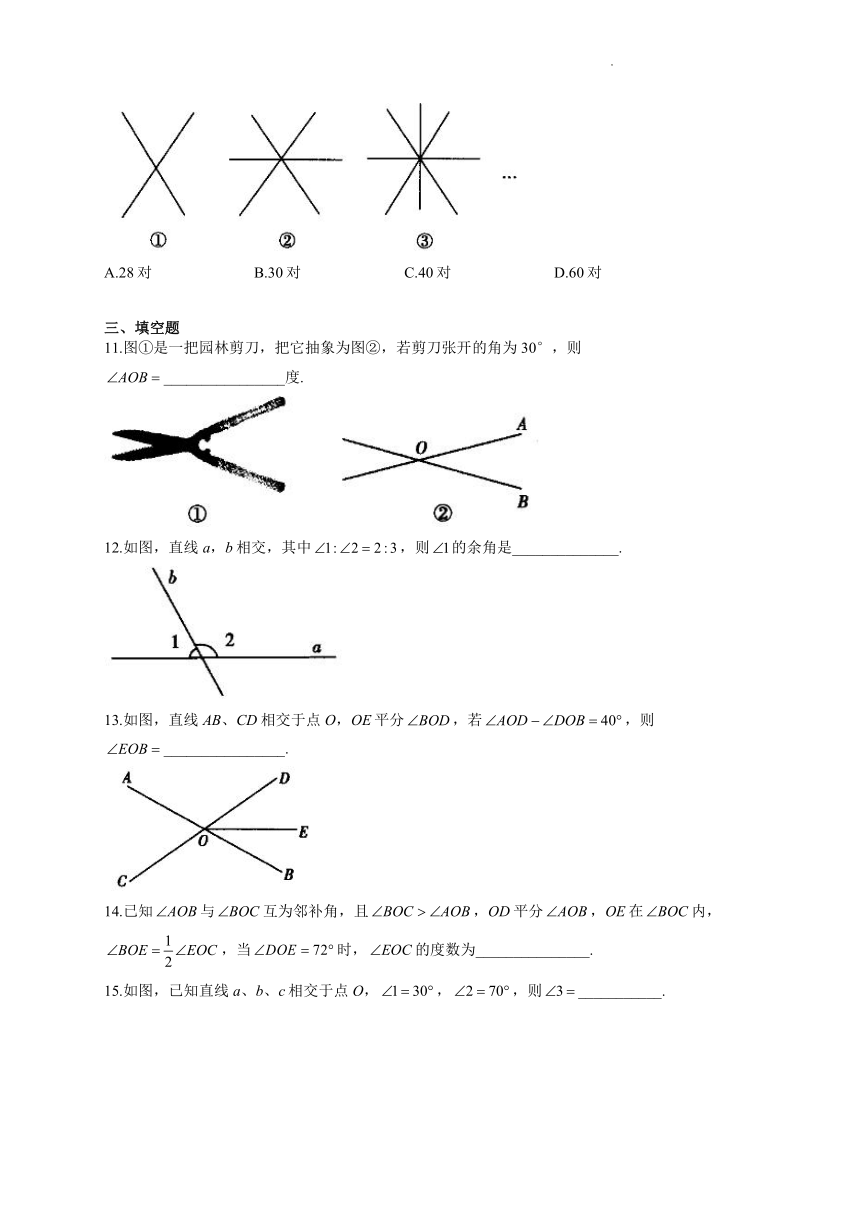
11.图①是一把园林剪刀,把它抽象为图②,若剪刀张开的角为30°,则________________度.
12.如图,直线a,b相交,其中,则的余角是______________.
13.如图,直线AB、CD相交于点O,OE平分,若,则________________.
14.已知与互为邻补角,且,OD平分,OE在内,,当时,的度数为_______________.
15.如图,已知直线a、b、c相交于点O,,,则___________.
三、解答题
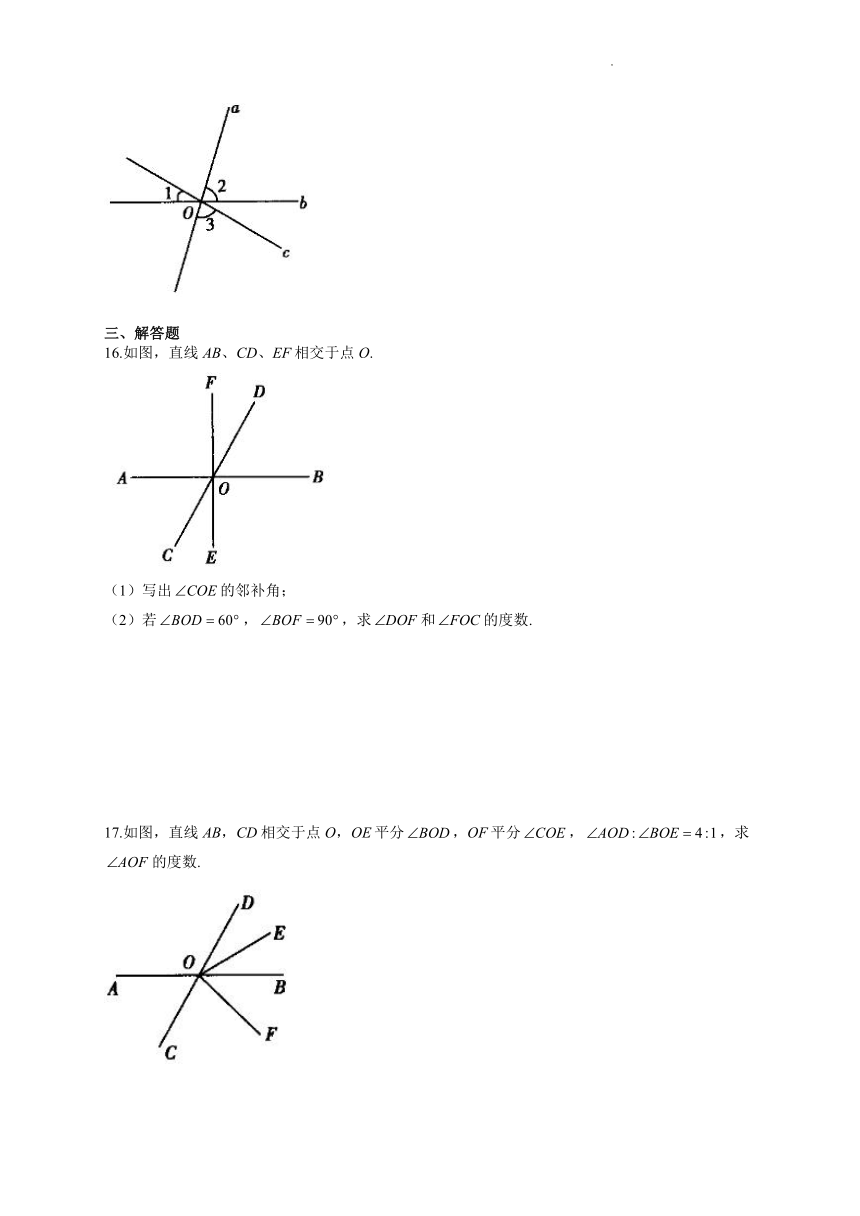
16.如图,直线AB、CD、EF相交于点O.
(1)写出的邻补角;
(2)若,,求和的度数.
17.如图,直线AB,CD相交于点O,OE平分,OF平分,,求的度数.
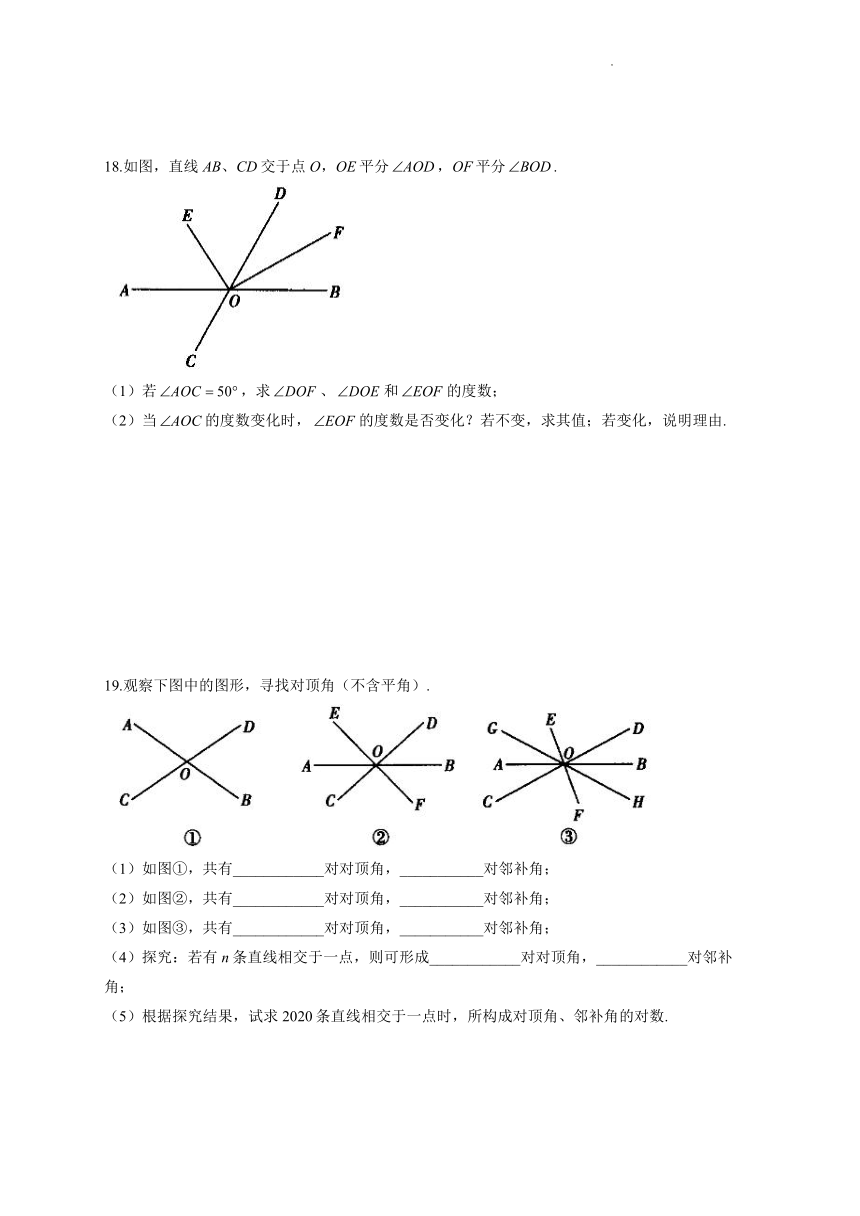
18.如图,直线AB、CD交于点O,OE平分,OF平分.
(1)若,求、和的度数;
(2)当的度数变化时,的度数是否变化?若不变,求其值;若变化,说明理由.
19.观察下图中的图形,寻找对顶角(不含平角).
(1)如图①,共有____________对对顶角,___________对邻补角;
(2)如图②,共有____________对对顶角,___________对邻补角;
(3)如图③,共有____________对对顶角,___________对邻补角;
(4)探究:若有n条直线相交于一点,则可形成____________对对顶角,____________对邻补角;
(5)根据探究结果,试求2020条直线相交于一点时,所构成对顶角、邻补角的对数.
参考答案
1.答案:A
解析:在同一平面内,不重合的两条直线有平行和相交两种位置关系.故选A.
2.答案:C
解析:与是对顶角的是C,
故选:C.
3.答案:D
解析:根据邻补角的定义可知,只有D中的与互为邻补角,其他都不符合题意.故选D.
4.答案:D
5.答案:A
解析:根据对顶角相等即可求解.
解:∵与是对顶角,
∴.
故选:A.
点评:本题考查了对顶角的识别与对顶角的性质,牢固掌握对顶角相等的性质是解题的关键.
6.答案:C
解析:与互为邻补角,
,又,
.
7.答案:C
解析:由对顶角相等,得,结合,得.由邻补角的定义,得.
8.答案:A
解析:因为与是对顶角,所以
,所以.因为射线OM平分,
所以,所以.故选A.
9.答案:C
解析:因为,所以.因为,所以.因为与是对顶角,所以.故选C.
10.答案:B
解析:6条直线交于一点时,对顶角的对数是.
11.答案:30
解析:由已知条件及对顶角的性质可知.
12.答案:18°
解析:因为与互为邻补角,所以,又因为,所以可设,则,所以,即,所以,其余角为.
13.答案:35°
解析:,,
,,
平分,
.
14.答案:72°
解析:如图,设,,则.
根据题意得,又,,,.
15.答案:80°
解析:如图,与,与,与分别互为对顶角,由对顶角相等,得,所以,又因为,,所以.
16.答案:(1)和
(2),
解析:(1)的邻补角是和.
(2),,.与互为邻补角,,.
17.答案:
解析:因为,
所以设,则.
因为OE平分,所以.
因为,所以,解得.
所以,,,所以.
因为OF平分,所以.
所以.
所以.
18.答案:(1),,
(2)的度数变化时,的度数不变,理由见解析
解析:(1)由对顶角相等得,
平分,.
平分,,
.
.
(2)的度数变化时,的度数不变.
平分,,
平分,,
.
19.答案:(1)2;4
(2)6;12
(3)12;24
(4);
(5)可形成4078380对对顶角,8156760对邻补角
解析:(1)共有对对顶角,对邻补角.
(2)共有对对顶角,对邻补角.
(3)共有对对顶角,对邻补角.
(4)若有n条直线相交于一点,则可形成对对顶角,对邻补角.
(5)2020条直线相交于一点时,可形成对对顶角,对邻补角.
5.1.1相交线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在同一平面内,不重合的两条直线的位置关系可能是( )
A.相交或平行 B.相交 C.平行 D.不能确定
2.下列图形中,与是对顶角的是( )
A. B. C. D.
3.下列各图中,与互为邻补角的是( )
A. B.
C. D.
4.下列说法正确的是( )
A.大小相等的两个角互为对顶角
B.有公共顶点且相等的两个角是对顶角
C.两角之和为180°,则这两个角互为邻补角
D.—个角的邻补角可能是锐角、钝角或直角
5.如图,直线a、b相交于点O,若等于50°,则等于( )
A.50° B.40° C.140° D.130°
6.如图,点O在直线AB上,若,则的大小是( )
A.60° B.90° C.120° D.150°
7.如图,直线AB与CD相交于点O,若,则等于( )
A.100° B.120° C.140° D.160°
8.如图,直线AB、CD相交于点O,射线OM平分,若,则等于( )
A.159° B.161° C.169° D.138°
9.如图,直线AB与CD相交于O点,,若,则的度数为( )
A. B. C. D.
10.如图①,两条直线交于一点,图中共有对对顶角:如图②,三条直线交于一点,图中共有对对顶角;如图③,四条直线交于一点,图中共有对对顶角;……,按这样的规律,六条直线交于一点,那么对顶角共有( )
A.28对 B.30对 C.40对 D.60对
三、填空题
11.图①是一把园林剪刀,把它抽象为图②,若剪刀张开的角为30°,则________________度.
12.如图,直线a,b相交,其中,则的余角是______________.
13.如图,直线AB、CD相交于点O,OE平分,若,则________________.
14.已知与互为邻补角,且,OD平分,OE在内,,当时,的度数为_______________.
15.如图,已知直线a、b、c相交于点O,,,则___________.
三、解答题
16.如图,直线AB、CD、EF相交于点O.
(1)写出的邻补角;
(2)若,,求和的度数.
17.如图,直线AB,CD相交于点O,OE平分,OF平分,,求的度数.
18.如图,直线AB、CD交于点O,OE平分,OF平分.
(1)若,求、和的度数;
(2)当的度数变化时,的度数是否变化?若不变,求其值;若变化,说明理由.
19.观察下图中的图形,寻找对顶角(不含平角).
(1)如图①,共有____________对对顶角,___________对邻补角;
(2)如图②,共有____________对对顶角,___________对邻补角;
(3)如图③,共有____________对对顶角,___________对邻补角;
(4)探究:若有n条直线相交于一点,则可形成____________对对顶角,____________对邻补角;
(5)根据探究结果,试求2020条直线相交于一点时,所构成对顶角、邻补角的对数.
参考答案
1.答案:A
解析:在同一平面内,不重合的两条直线有平行和相交两种位置关系.故选A.
2.答案:C
解析:与是对顶角的是C,
故选:C.
3.答案:D
解析:根据邻补角的定义可知,只有D中的与互为邻补角,其他都不符合题意.故选D.
4.答案:D
5.答案:A
解析:根据对顶角相等即可求解.
解:∵与是对顶角,
∴.
故选:A.
点评:本题考查了对顶角的识别与对顶角的性质,牢固掌握对顶角相等的性质是解题的关键.
6.答案:C
解析:与互为邻补角,
,又,
.
7.答案:C
解析:由对顶角相等,得,结合,得.由邻补角的定义,得.
8.答案:A
解析:因为与是对顶角,所以
,所以.因为射线OM平分,
所以,所以.故选A.
9.答案:C
解析:因为,所以.因为,所以.因为与是对顶角,所以.故选C.
10.答案:B
解析:6条直线交于一点时,对顶角的对数是.
11.答案:30
解析:由已知条件及对顶角的性质可知.
12.答案:18°
解析:因为与互为邻补角,所以,又因为,所以可设,则,所以,即,所以,其余角为.
13.答案:35°
解析:,,
,,
平分,
.
14.答案:72°
解析:如图,设,,则.
根据题意得,又,,,.
15.答案:80°
解析:如图,与,与,与分别互为对顶角,由对顶角相等,得,所以,又因为,,所以.
16.答案:(1)和
(2),
解析:(1)的邻补角是和.
(2),,.与互为邻补角,,.
17.答案:
解析:因为,
所以设,则.
因为OE平分,所以.
因为,所以,解得.
所以,,,所以.
因为OF平分,所以.
所以.
所以.
18.答案:(1),,
(2)的度数变化时,的度数不变,理由见解析
解析:(1)由对顶角相等得,
平分,.
平分,,
.
.
(2)的度数变化时,的度数不变.
平分,,
平分,,
.
19.答案:(1)2;4
(2)6;12
(3)12;24
(4);
(5)可形成4078380对对顶角,8156760对邻补角
解析:(1)共有对对顶角,对邻补角.
(2)共有对对顶角,对邻补角.
(3)共有对对顶角,对邻补角.
(4)若有n条直线相交于一点,则可形成对对顶角,对邻补角.
(5)2020条直线相交于一点时,可形成对对顶角,对邻补角.
