2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 186.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 18:27:16 | ||
图片预览

文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
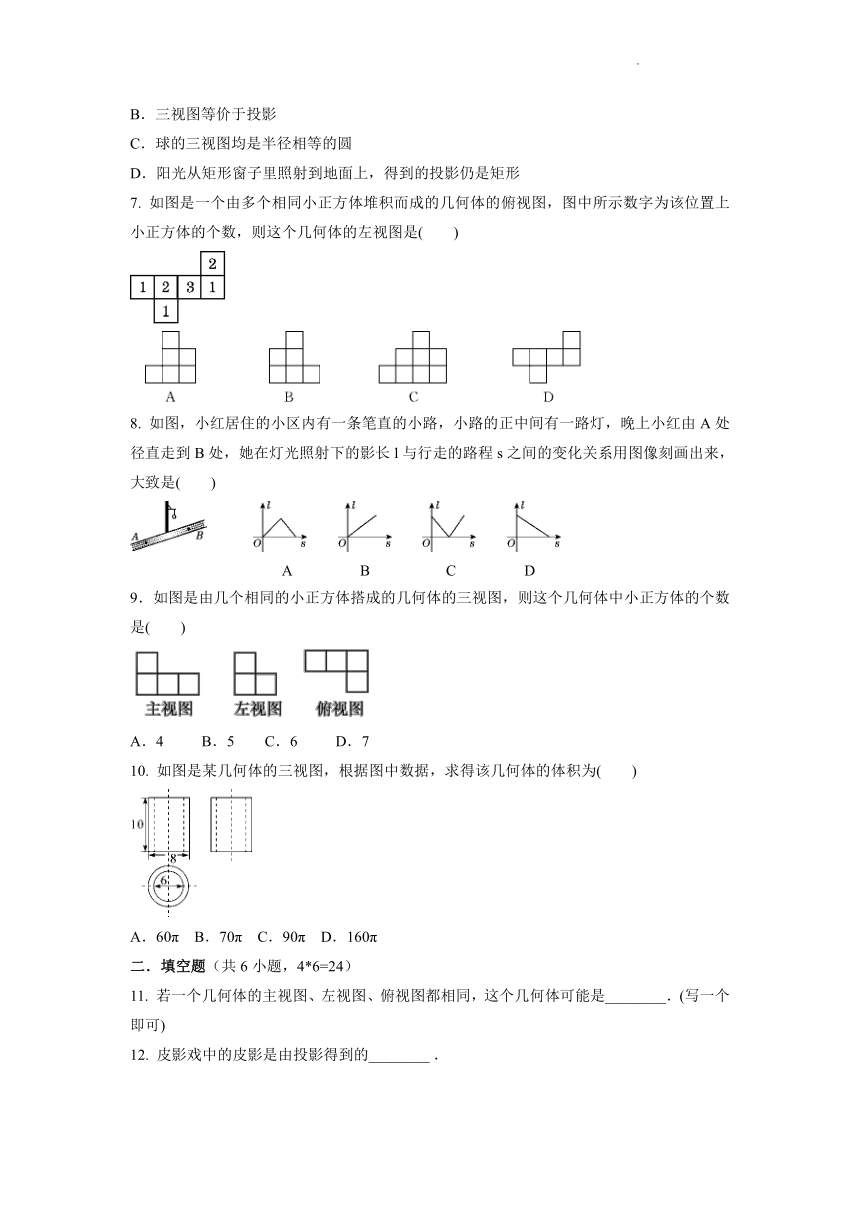
1. 如图,这是一个长方体包装盒,则它的表面展开图可能是( )
2. 如图所示的几何体的主视图为( )
3. 有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )
4. 王丽同学在某天下午的不同时刻拍了三张同一景物的风景照A,B,C,冲洗后不知道拍照的顺序,已知投影lA>lC>lB,则A,B,C的先后顺序是( )
A.A,B,C B.A,C,B
C.B,C,A D.B,A,C
5. 如图是某几何体的三视图,则该几何体是( )
A. 正方体 B. 圆锥体
C. 圆柱体 D. 球体
6. 下列命题正确的是( )
A.三视图是中心投影
B.三视图等价于投影
C.球的三视图均是半径相等的圆
D.阳光从矩形窗子里照射到地面上,得到的投影仍是矩形
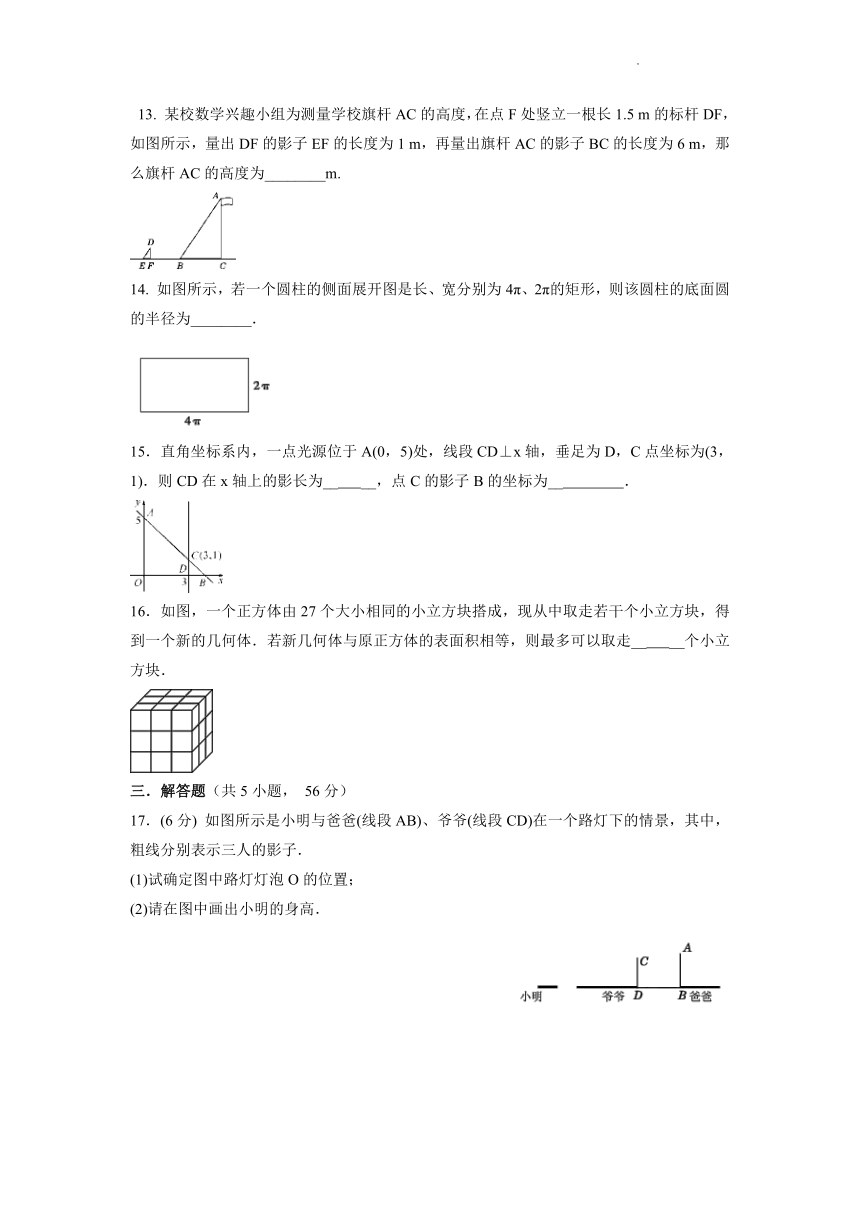
7. 如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置上小正方体的个数,则这个几何体的左视图是( )
8. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图像刻画出来,大致是( )
A B C D
9.如图是由几个相同的小正方体搭成的几何体的三视图,则这个几何体中小正方体的个数是( )
A.4 B.5 C.6 D.7
10. 如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D.160π
二.填空题(共6小题,4*6=24)
11. 若一个几何体的主视图、左视图、俯视图都相同,这个几何体可能是________.(写一个即可)
12. 皮影戏中的皮影是由投影得到的________ .
13. 某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长1.5 m的标杆DF,如图所示,量出DF的影子EF的长度为1 m,再量出旗杆AC的影子BC的长度为6 m,那么旗杆AC的高度为________m.
14. 如图所示,若一个圆柱的侧面展开图是长、宽分别为4π、2π的矩形,则该圆柱的底面圆的半径为________.
15.直角坐标系内,一点光源位于A(0,5)处,线段CD⊥x轴,垂足为D,C点坐标为(3,1).则CD在x轴上的影长为__ __,点C的影子B的坐标为__ .
16.如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走__ __个小立方块.
三.解答题(共5小题, 56分)
17.(6分) 如图所示是小明与爸爸(线段AB)、爷爷(线段CD)在一个路灯下的情景,其中,粗线分别表示三人的影子.
(1)试确定图中路灯灯泡O的位置;
(2)请在图中画出小明的身高.
18.(8分) 由几个边长为1的小立方块搭成的几何体的俯视图如图所示,正方形中的数字表示该位置的小立方块的个数.
(1)这个几何体的体积为________个立方单位;
(2)请在下图方格纸中分别画出该几何体的主视图和左视图.
19.(8分) 《孙子算经》中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何?”
友情提醒:①歌谣的意思:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺,同时立一根一尺五寸的标杆,它的影长为五寸.请你算一算竹竿的长度是多少.
②丈和尺是古代的长度单位,1丈=10尺,1尺=10寸.
20.(10分) 如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.
21.(12分) 如图是一个圆柱体零件,削去了上底面圆的四分之一部分的柱体,现已画出了主视图与俯视图.
(1)画出此零件的左视图;
(2)若此零件高h=3cm,且其俯视图恰好可以卷成底面半径为1.5cm的圆锥,求此零件的表面积.
22.(12分) 如图,花丛中有一根路灯杆AB,在灯光下小明在点D处的影长DE=3 m,沿BD方向行走到达点G,测得DG=5 m,这时小明的影长GH=5 m.如果小明的身高为1.7 m,求路灯杆AB的高度.
参考答案
1-5ABDCC 6-10CBCBD
11.球体(或正方体)
12.中心投影
13.9
14. 1或2
15. ,(,0)
16.6
17.解:(1)如图所示,O为灯泡的位置
(2)EF即为小明的身高
18. 解:(1)6
(2)如图所示.
19.解:竹竿的影长为一丈五尺=15尺,标杆长为一尺五寸=1.5尺,影长为五寸=0.5尺,设竹竿的长度为x尺,根据题意,得x∶15 =1.5∶0.5 ,解得x=45.答:竹竿的长度是45尺.
20.解:根据三视图,可知下面的长方体的长、宽、高分别为8mm,6mm,2mm,上面的长方体的长、宽、高分别为4mm,2mm,4mm.则这个立体图形的表面积为2(8×6+6×2+8×2)+2(4×2+2×4+4×4)-2×4×2=200(mm2).答:这个立体图形的表面积为200mm2.
21. (1)左视图与主视图形状相同,图略;
(2)由2π×1.5=,解得:r=2,两个底面积=2πr2×=6π(cm2),侧面积=(2πr×+2r)×h=(9π+12)cm2,表面积=(15π+12)cm2,答:此零件的表面积为(15π+12)cm2.
22. 解:由题意,得AB⊥BH,CD⊥BH,FG⊥BH.在△ABE和△CDE中,∵AB⊥BH,CD⊥BH,∴CD∥AB.∴△ABE∽△CDE.∴=.同理可得△ABH∽△FGH,∴=.又∵CD=FG=1.7 m,∴=.∵DE=3 m,DG=5 m,GH=5 m,∴=,解得BD=7.5 m.∴AB===5.95(m).答:路灯杆AB的高度为5.95 m.
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 如图,这是一个长方体包装盒,则它的表面展开图可能是( )
2. 如图所示的几何体的主视图为( )
3. 有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )
4. 王丽同学在某天下午的不同时刻拍了三张同一景物的风景照A,B,C,冲洗后不知道拍照的顺序,已知投影lA>lC>lB,则A,B,C的先后顺序是( )
A.A,B,C B.A,C,B
C.B,C,A D.B,A,C
5. 如图是某几何体的三视图,则该几何体是( )
A. 正方体 B. 圆锥体
C. 圆柱体 D. 球体
6. 下列命题正确的是( )
A.三视图是中心投影
B.三视图等价于投影
C.球的三视图均是半径相等的圆
D.阳光从矩形窗子里照射到地面上,得到的投影仍是矩形
7. 如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置上小正方体的个数,则这个几何体的左视图是( )
8. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图像刻画出来,大致是( )
A B C D
9.如图是由几个相同的小正方体搭成的几何体的三视图,则这个几何体中小正方体的个数是( )
A.4 B.5 C.6 D.7
10. 如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D.160π
二.填空题(共6小题,4*6=24)
11. 若一个几何体的主视图、左视图、俯视图都相同,这个几何体可能是________.(写一个即可)
12. 皮影戏中的皮影是由投影得到的________ .
13. 某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长1.5 m的标杆DF,如图所示,量出DF的影子EF的长度为1 m,再量出旗杆AC的影子BC的长度为6 m,那么旗杆AC的高度为________m.
14. 如图所示,若一个圆柱的侧面展开图是长、宽分别为4π、2π的矩形,则该圆柱的底面圆的半径为________.
15.直角坐标系内,一点光源位于A(0,5)处,线段CD⊥x轴,垂足为D,C点坐标为(3,1).则CD在x轴上的影长为__ __,点C的影子B的坐标为__ .
16.如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走__ __个小立方块.
三.解答题(共5小题, 56分)
17.(6分) 如图所示是小明与爸爸(线段AB)、爷爷(线段CD)在一个路灯下的情景,其中,粗线分别表示三人的影子.
(1)试确定图中路灯灯泡O的位置;
(2)请在图中画出小明的身高.
18.(8分) 由几个边长为1的小立方块搭成的几何体的俯视图如图所示,正方形中的数字表示该位置的小立方块的个数.
(1)这个几何体的体积为________个立方单位;
(2)请在下图方格纸中分别画出该几何体的主视图和左视图.
19.(8分) 《孙子算经》中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何?”
友情提醒:①歌谣的意思:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺,同时立一根一尺五寸的标杆,它的影长为五寸.请你算一算竹竿的长度是多少.
②丈和尺是古代的长度单位,1丈=10尺,1尺=10寸.
20.(10分) 如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.
21.(12分) 如图是一个圆柱体零件,削去了上底面圆的四分之一部分的柱体,现已画出了主视图与俯视图.
(1)画出此零件的左视图;
(2)若此零件高h=3cm,且其俯视图恰好可以卷成底面半径为1.5cm的圆锥,求此零件的表面积.
22.(12分) 如图,花丛中有一根路灯杆AB,在灯光下小明在点D处的影长DE=3 m,沿BD方向行走到达点G,测得DG=5 m,这时小明的影长GH=5 m.如果小明的身高为1.7 m,求路灯杆AB的高度.
参考答案
1-5ABDCC 6-10CBCBD
11.球体(或正方体)
12.中心投影
13.9
14. 1或2
15. ,(,0)
16.6
17.解:(1)如图所示,O为灯泡的位置
(2)EF即为小明的身高
18. 解:(1)6
(2)如图所示.
19.解:竹竿的影长为一丈五尺=15尺,标杆长为一尺五寸=1.5尺,影长为五寸=0.5尺,设竹竿的长度为x尺,根据题意,得x∶15 =1.5∶0.5 ,解得x=45.答:竹竿的长度是45尺.
20.解:根据三视图,可知下面的长方体的长、宽、高分别为8mm,6mm,2mm,上面的长方体的长、宽、高分别为4mm,2mm,4mm.则这个立体图形的表面积为2(8×6+6×2+8×2)+2(4×2+2×4+4×4)-2×4×2=200(mm2).答:这个立体图形的表面积为200mm2.
21. (1)左视图与主视图形状相同,图略;
(2)由2π×1.5=,解得:r=2,两个底面积=2πr2×=6π(cm2),侧面积=(2πr×+2r)×h=(9π+12)cm2,表面积=(15π+12)cm2,答:此零件的表面积为(15π+12)cm2.
22. 解:由题意,得AB⊥BH,CD⊥BH,FG⊥BH.在△ABE和△CDE中,∵AB⊥BH,CD⊥BH,∴CD∥AB.∴△ABE∽△CDE.∴=.同理可得△ABH∽△FGH,∴=.又∵CD=FG=1.7 m,∴=.∵DE=3 m,DG=5 m,GH=5 m,∴=,解得BD=7.5 m.∴AB===5.95(m).答:路灯杆AB的高度为5.95 m.
