4.8.2平行线的判定

课件24张PPT。 平行线的判定学习目标1.经历“平行线的判定方法”的发现过程。
2.掌握平行线的判定方法。
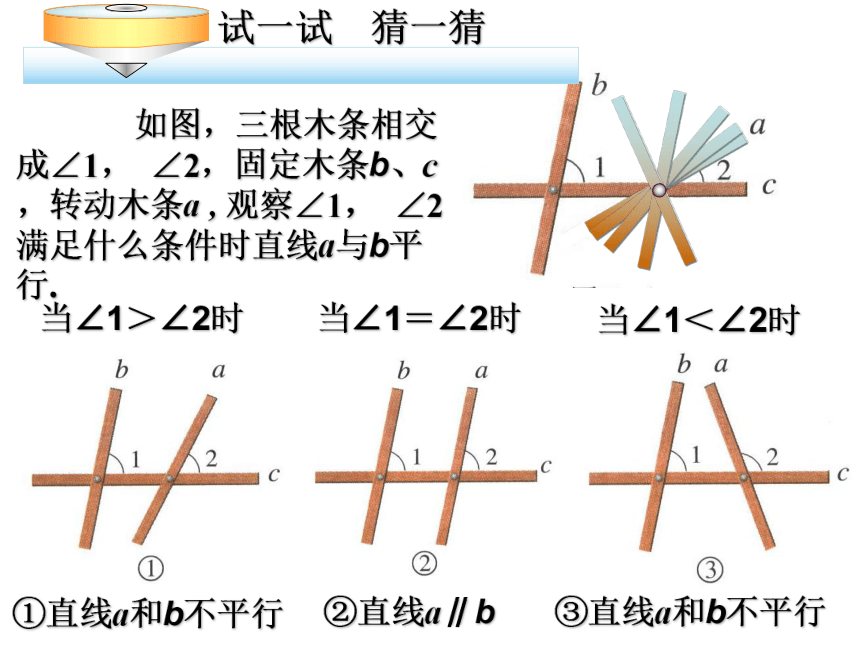
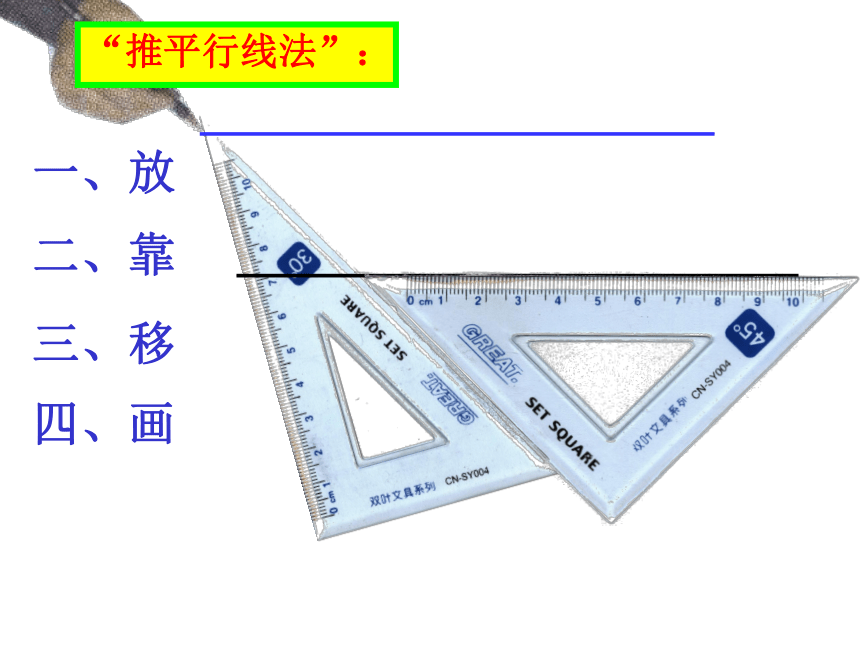
3. 会用它进行简单的推理和表述。 如图，三根木条相交成∠1， ∠2，固定木条b、c，转动木条a , 观察∠1， ∠2满足什么条件时直线a与b平行.当∠1＞∠2时当∠1＝∠2时当∠1＜∠2时①直线a和b不平行②直线a∥b③直线a和b不平行一、放二、靠三、移四、画“推平行线法”： 请按图 1-5 所示方法画两条平行线,然后讨论下面的问题: (1)上面的画法可以看做是怎样的图形变换? (2) 把图中的直线 , 看成被尺边 所截,那么在画图过程中,什么角始终保持相等?由此你能发现画两直线平行方法的依据吗?想一想！ 两条直线被第三条直线所截，
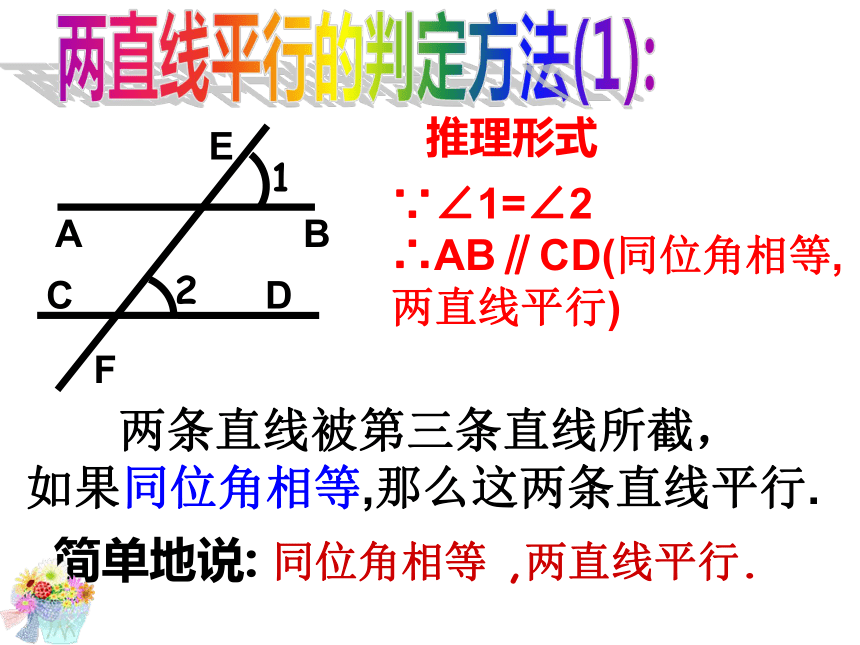
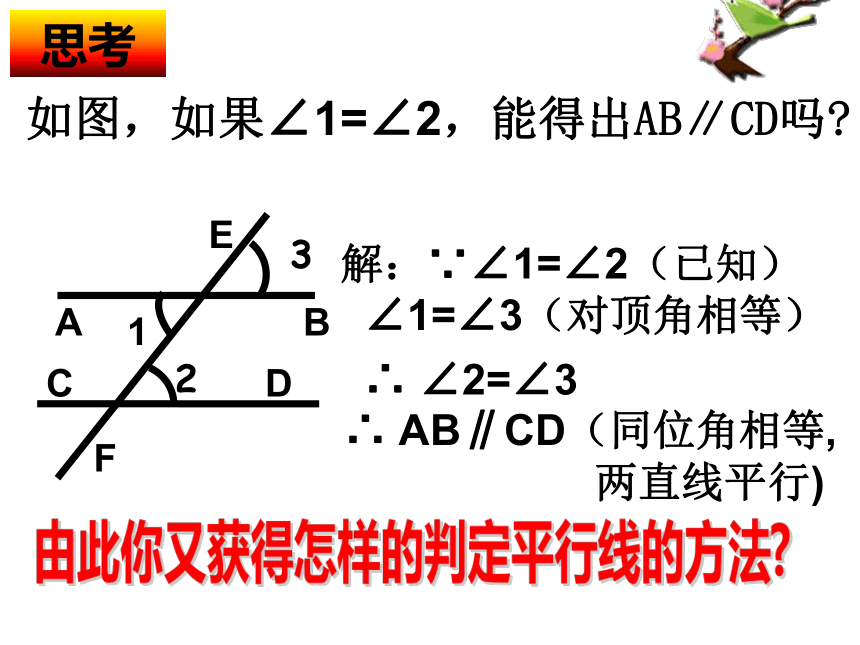
如果同位角相等,那么这两条直线平行.简单地说: 同位角相等 ,两直线平行.两直线平行的判定方法(1):BACDF12E如图，如果∠1=∠2，能得出AB∥CD吗?思考解：∵∠1=∠2（已知）
∠1=∠3（对顶角相等）
∴ ∠2=∠3∴ AB∥CD（同位角相等,
两直线平行)B1ACDF32E由此你又获得怎样的判定平行线的方法? 两条直线被第三条直线所截，
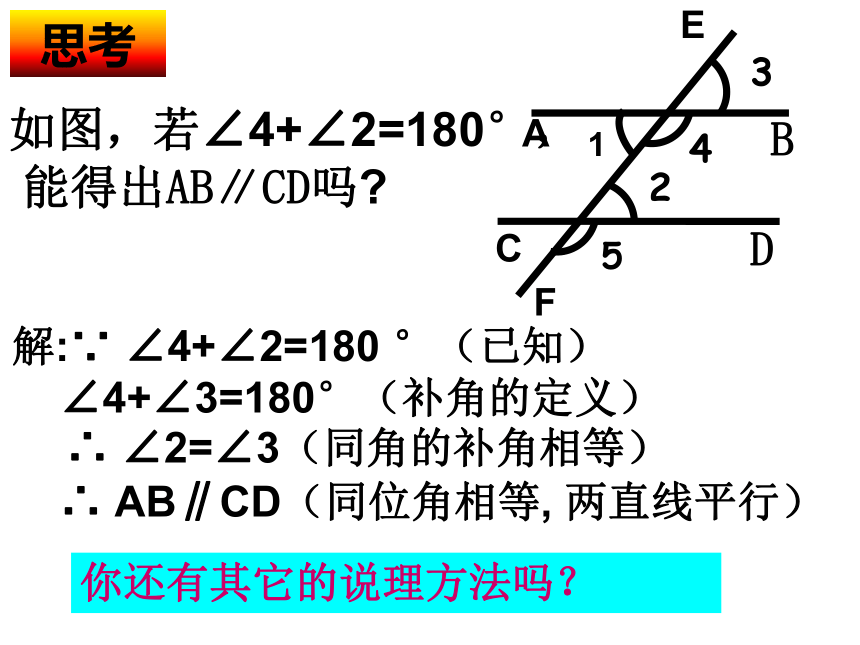
如果内错角相等,那么这两条直线平行.C简单地说: 内错角相等 ,两直线平行.两直线平行的判定方法(2):如图，若∠4+∠2=180°，
能得出AB∥CD吗?思考解:∵ ∠4+∠2=180 °（已知）
∠4+∠3=180°（补角的定义）
∴ ∠2=∠3（同角的补角相等）∴ AB∥CD（同位角相等, 两直线平行）1AC3425DBEF你还有其它的说理方法吗？如图，如果
∠4+∠2=180°，
能得出AB∥CD?思考解∵ ∠4+∠2=180 °（已知） ∠4+∠1=180°（补角的定义）
∴ ∠2=∠1（同角的补角相等）∴ AB∥CD（内错角相等, 两直线平行）1AC3425DBEF 两条直线被第三条直线所截，
如果同旁内角互补,那么这两条直线平行.简单地说:同旁内角互补,两直线平行.两直线平行的判定方法（3）例 1已知直线l1 ，l2被l3所截,如图，
∠1＝45°,∠2＝135°,试
判断l1与l2是否平行.并说明理由.试一试1.如图，哪些直线平行，哪些直线不平行?请说明理由.2.街道两侧路灯的柱子是否平行?213.“在同一平面内,垂直于同一条直线的两条直线互相平行”是否可以看作平行线判定的特殊情形?　　
， ， （已知）　　 （垂直的定义）　　 （同位角相等，两直线平行） ∴解:∵b⊥a ， c⊥a∠1 =∠2=90° ∴b∥c 在同一平面内,垂直于同一条直线的两条直线互相平行推理格式：
∵b⊥a ， c⊥a ∴b∥c平行线判定1的推论：如图：在下列条件下可判定哪两直线平行，并说明根据。
（1）∠1＝∠2；（2） ∠3＝∠A；
（3） ∠A+∠2 +∠4＝180°.初试牛刀火眼金睛
1.找出图中的平行线如果∠ADE=∠ABC,则＿＿∥ ＿＿如果∠ACD=∠F, 则＿＿∥ ＿＿如果∠DEC=∠BCF,则＿＿∥ ＿＿注：要确定是哪两条直线被第三条直线所截得到的同位角2.如图,已知∠ABD=∠ACE，BF、CG分别是∠ABD、∠ACE的平分线，请判断BF与CG是否平行，并说明理由。1想一想1.如图，AB⊥BC于B，
∠1=125°，∠2=35°，
请说明l1∥l2的理由。2.如图，∠B=40°，∠DFC=140 ° ，
试判断AB与DE是否平行，
并说明理由。理一理 你学到了什么？
你认为还有什么不懂的？
你有什么经验与收获让同学们共享呢？1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行，
那么这两条直线也互相平行.
5.如果两条直线都与第三条直线垂直，
那么这两条直线也互相平行.
6.平行线的定义.
判定两条直线是否平行的方法有：课本176页3、4作业：