2021-2022学年鲁教版(五四制)八年级数学下册6.3正方形的性质与判定同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.3正方形的性质与判定同步达标测试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 279.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 22:32:12 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》
同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.下列关于 ABCD的叙述,正确的是( )
A.若AC=BD,则 ABCD是矩形 B.若AB=AD,则 ABCD是正方形
C.若AB⊥BC,则 ABCD是菱形 D.若AC⊥BD,则 ABCD是正方形
2.如图,正方形ABCD的面积为4,菱形AECF的面积为2,则EF的长是( )
A.1 B. C.2 D.2
3.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
4.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=6,F为DE的中点.若OF的长为1,则△CEF的周长为( )
A.14 B.16 C.18 D.12
5.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2 B.3 C. D.
6.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣2,0),B(2,b),则正方形ABCD的面积是( )
A.34 B.25 C.20 D.16
7.如图,正方形ABCD的边长为2,E为AB边的中点,点F在BC边上,点B关于直线EF的对称点记为B',连接B'D,B'E,B'F.当点F在BC边上移动使得四边形BEB'F成为正方形时,B'D的长为( )
A. B. C.2 D.3
8.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:①AP=EF;②∠PFE=∠BAP;③PD=EC;④△APD一定是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题,满分35分)
9.用4张全等的直角三角形纸片拼接成如图所示的图案,得到两个大小不同的正方形.若正方形ABCD的面积为10,AH=3,则正方形EFGH的面积为 .
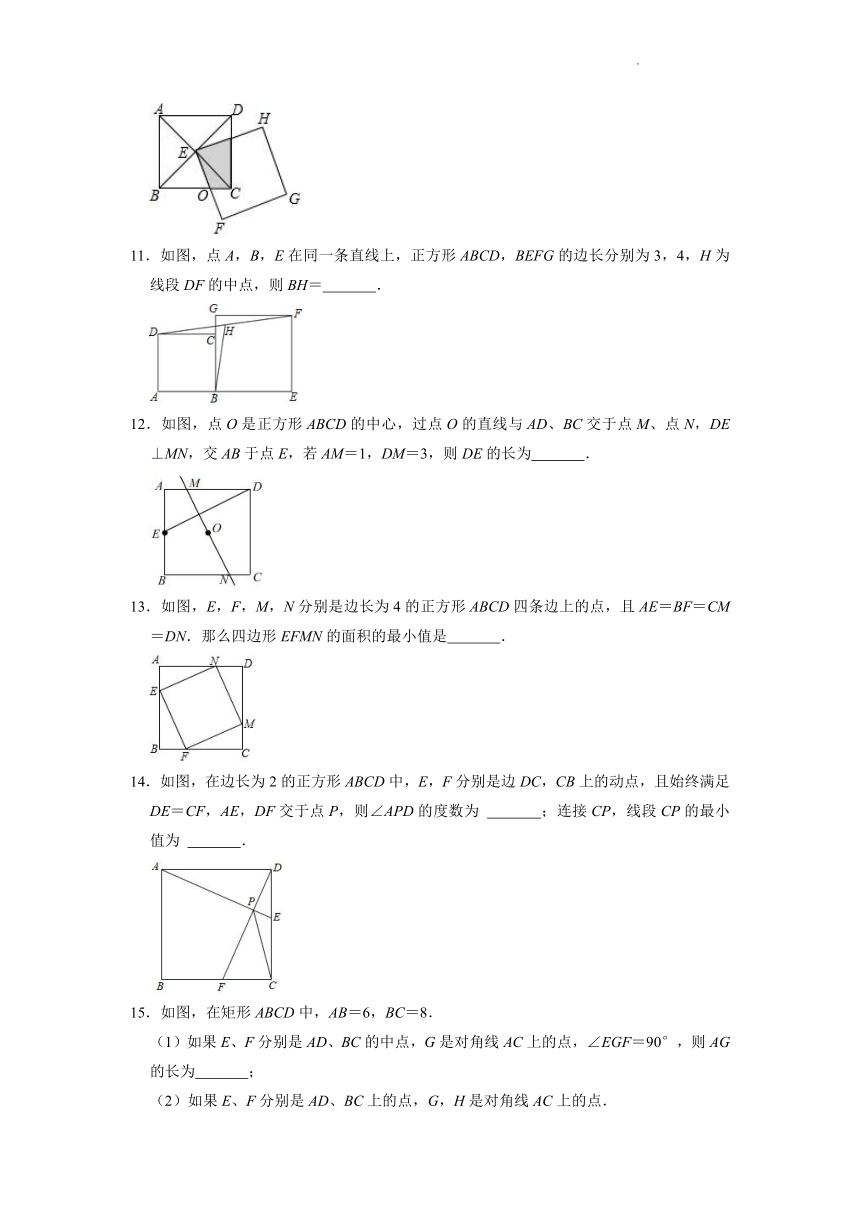
10.已知:如图,正方形ABCD和EFGH的边长都等于1,点E恰好是AC、BD的交点,则两个正方形的重叠部分(阴影部分)的面积是 .
11.如图,点A,B,E在同一条直线上,正方形ABCD,BEFG的边长分别为3,4,H为线段DF的中点,则BH= .
12.如图,点O是正方形ABCD的中心,过点O的直线与AD、BC交于点M、点N,DE⊥MN,交AB于点E,若AM=1,DM=3,则DE的长为 .
13.如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是 .
14.如图,在边长为2的正方形ABCD中,E,F分别是边DC,CB上的动点,且始终满足DE=CF,AE,DF交于点P,则∠APD的度数为 ;连接CP,线段CP的最小值为 .
15.如图,在矩形ABCD中,AB=6,BC=8.
(1)如果E、F分别是AD、BC的中点,G是对角线AC上的点,∠EGF=90°,则AG的长为 ;
(2)如果E、F分别是AD、BC上的点,G,H是对角线AC上的点.
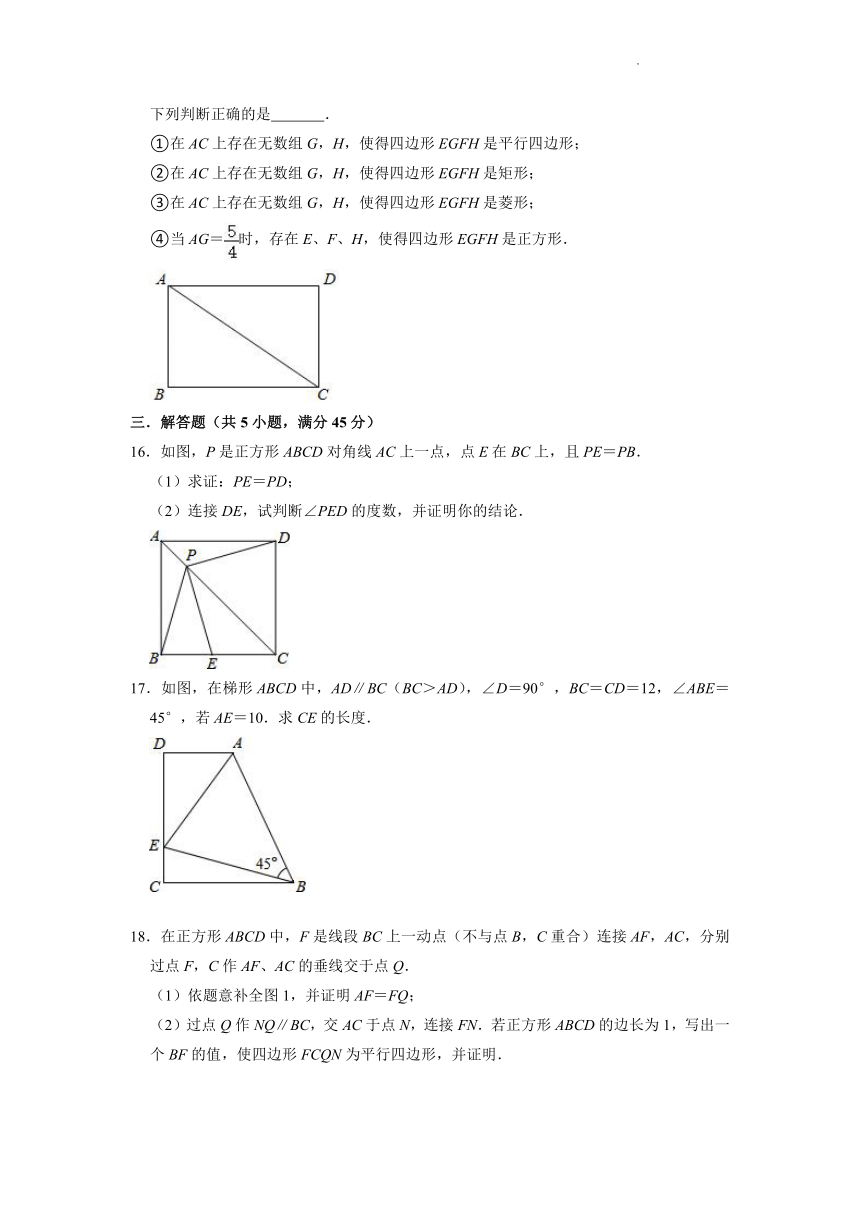
下列判断正确的是 .
①在AC上存在无数组G,H,使得四边形EGFH是平行四边形;
②在AC上存在无数组G,H,使得四边形EGFH是矩形;
③在AC上存在无数组G,H,使得四边形EGFH是菱形;
④当AG=时,存在E、F、H,使得四边形EGFH是正方形.
三.解答题(共5小题,满分45分)
16.如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
17.如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
18.在正方形ABCD中,F是线段BC上一动点(不与点B,C重合)连接AF,AC,分别过点F,C作AF、AC的垂线交于点Q.
(1)依题意补全图1,并证明AF=FQ;
(2)过点Q作NQ∥BC,交AC于点N,连接FN.若正方形ABCD的边长为1,写出一个BF的值,使四边形FCQN为平行四边形,并证明.
19.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
20.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵ ABCD中,AC=BD,
∴四边形ABCD是矩形,选项A符合题意;
∵ ABCD中,AB=AD,
∴四边形ABCD是菱形,不一定是正方形,选项B不符合题意;
∵ ABCD中,AB⊥BC,
∴四边形ABCD是矩形,不一定是菱形,选项C不符合题意;
∵ ABCD中,AC⊥BD,
∴四边形ABCD是菱形,选项D不符合题意;
故选:A.
2.解:连接AC,
∵正方形ABCD的面积为4,
∴AC2=4,
解得AC=,
∵菱形AECF的面积为2,
∴AC EF=2,
即×EF=2,
解得EF=,
故选:B.
3.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
4.解:在正方形ABCD中,BO=DO,BC=CD,∠BCD=90°,
∵F为DE的中点,
∴OF为△DBE的中位线,ED=2CF=2EF,
∴△CEF的周长为EF+EC+FC=ED+EC,
∵OF=1,
∴BE=2OF=2,
∵CE=6,
∴BC=BE+CE=2+6=8,
∴CD=BC=8,
在Rt△CED中,∠ECD=90°,CD=8,CE=6,
∴ED=,
∴△CEF的周长为EF+EC+FC=ED+EC=10+6=16,
故选:B.
5.解:过B点作BF⊥CD,与DC的延长线交于F点,
则有△BCF≌△BAE(ASA),
则BE=BF,S四边形ABCD=S正方形BEDF=8,
∴BE==.
故选:C.
6.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣2,0),B(2,b),
∴OA=2,OM=2,
∴OD=AM=4,
∴AD===2,
∴正方形ABCD的面积=2×2=20,
故选:C.
7.解:如图,连接BB',连接BD,
∵四边形ABCD是正方形,
∴BD=AB=2,BD平分∠ABC,
∵E为AB边的中点,
∴AE=BE=1,
∵四边形BEB'F是正方形,
∴BB'=BE=,BB'平分∠ABC,
∴点B,点B',点D三点共线,
∴B'D=BD﹣BB'=,
故选:A.
8.解:作PH⊥AB于H,
∴∠PHB=90°,
∵PE⊥BC,PF⊥CD,
∴∠PEB=∠PEC=∠PFC=90°.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠1=∠2=∠BDC=45°,∠ABC=∠C=90°,
∴四边形BEPH和四边形PECF是矩形,PE=BE,DF=PF,
∴四边形BEPH为正方形,
∴BH=BE=PE=HP,
∴AH=CE,
∴△AHP≌△FPE,
∴AP=EF,∠PFE=∠BAP,
故①、②正确,
在Rt△PDF中,由勾股定理,得
PD=PF,
∴PD=CE.
故③正确.
∵点P在BD上,
∴当AP=AD、PA=PD或DA=DP时△APD是等腰三角形.
∴△APD是等腰三角形只有三种情况.
故④错误,
∴正确的个数有3个.
故选:C.
二.填空题(共7小题,满分35分)
9.解:∵正方形ABCD的面积为10,
∴AD2=10,
∴DH===1,
∵△AHD≌△DGC,
∴AH=DG=3,
∴HG=DG﹣DH=2,
∴正方形EFGH的面积=HG2=4,
故答案为:4.
10.解:∵四边形ABCD是正方形,
∴EC=ED,∠DEC=90°,
∵四边形EFGH是正方形,
∴∠FEH=90°,
∴∠OEC=∠MED,
在△OEC和△MED中,
,
∴△OEC≌△MED(ASA)
∴两个正方形的重叠部分(阴影部分)的面积=△DEC的面积=×正方形ABCD的面积=0.25,故答案为:0.25.
11.解:连接BD、BF,
∵四边形ABCD,BEFG是正方形,且边长分别为3和4,
∴∠DBC=∠GBF=45°,BD=3,BF=4,
∴∠DBF=90°,
由勾股定理得:DF==5,
∵H为线段DF的中点,
∴BH=DF=.
故答案为:.
12.解:如图,连接AC,过点A作AF∥MN,交BC于F,
∵AM=1,DM=3,
∴AD=4,
∵点O是正方形ABCD的中心,
∴AO=CO,AB=AD=BC=4,∠ABC=∠BAD=90°,AD∥BC,
∴∠MAO=∠NCO,
又∵∠AOM=∠CON,AO=CO,
∴△AMO≌△CNO(ASA),
∴AM=CN=1,
∵AD∥BC,AF∥MN,
∴四边形AMNF是平行四边形,
∴AM=FN=1,
∴BF=2,
∵DE⊥MN,AF∥MN,
∴DE⊥AF,
∴∠AED+∠EAF=90°,
又∵∠EAF+∠AFB=90°,
∴∠AED=∠AFB,
又∵∠EAD=∠ABF=90°,AD=AB,
∴△ADE≌△BAF(AAS),
∴AE=BF=2,
∴DE===2,
故答案为2.
13.解:∵AE=BF=CM=DN,
∴AN=DM=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEN≌△DMN≌△CFM≌△BEF.
∴EF=EN=NM=MF,∠ENA=∠DMN.
∴四边形EFMN是菱形.
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,
∴∠ENA+∠DNM=90°.
∴∠ENM=90°.
∴四边形EFMN是正方形,
∴EN最小时,正方形EFMN的面积最小,设AE=DN=x,
则EN==,
∴x=2时,EN的值最小,最小值=,
∴正方形EFMN的面积=()2=8.
14.解:∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠DCF=90°,
在△ADE和△DCF中,
,
∴△ADE≌△DCF(SAS),
∴∠DAE=∠CDF,
∵∠CDF+∠ADF=∠ADC=90°,
∴∠ADF+∠DAE=90°,
∴∠APD=90°,
取AD的中点O,连接OP,则OP=AD=×2=1(不变),
根据两点之间线段最短得C、P、O三点共线时线段CP的值最小,
在Rt△COD中,根据勾股定理得,CO===,
所以,CP=CO﹣OP=﹣1.
故答案为:90°,﹣1.
15.解:(1)如图,
∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,AD=BC,
∴AC===10,
∵AD∥BC,
∴∠EAO=∠FCO,
∵E、F分别是AD、BC的中点,
∴AE=CF=BF=DE,
∴四边形ABFE是平行四边形,
∴EF=AB=6,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(AAS),
∴EO=FO=3,AO=CO=5,
当点G在点O上方时,∵∠EGF=90°,EO=FO,
∴GO=EO=3,
∴AG=AO﹣GO=5﹣3=2,
当点G'在点O下方时,∵∠EG'F=90°,EO=FO,
∴G'O=EO=3,
∴AG'=AO+G'O=5+3=8,
综上所述:AG=2或8;
(2)①在AC上存在无数组G,H,使得四边形EGFH是平行四边形,故该说法正确;
②在AC上存在无数组G,H,使得四边形EGFH是矩形,故该说法正确;
③在AC上存在无数组G,H,使得四边形EGFH是菱形,故该说法正确;
④当AG=时,存在E、F、H,使得四边形EGFH是正方形,
故答案为①②③④.
三.解答题(共5小题,满分45分)
16.(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)判断∠PED=45°.
证明:∵四边形ABCD是正方形,
∴∠BCD=90°,
∵△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
在四边形PECD中,∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴∠PED=45°.
17.解:过B作DA的垂线交DA的延长线于M,M为垂足,
延长DM到G,使MG=CE,连接BG,
易知四边形BCDM是正方形,
则△BEC与△BGM中,
,
∴△BEC≌△BMG(SAS),
∴∠MBG=∠CBE,BE=BG,
∵∠ABE=45°,
∴∠CBE+∠ABM=∠MBG+∠ABM=45°,
即∠ABE=∠ABG=45°,
在△ABE与△ABG中,
,
∴△ABE≌△ABG(SAS),
∴AG=AE=10,
设CE=x,则AM=10﹣x,
AD=12﹣(10﹣x)=2+x,DE=12﹣x,
在Rt△ADE中,AE2=AD2+DE2,
∴100=(x+2)2+(12﹣x)2,
即x2﹣10x+24=0;
解得:x1=4,x2=6.
故CE的长为4或6.
18.解:(1)根据题意,作图如下:
证明:在AB上截取BM=BF,如下图,
∵∠CFQ+∠AFB=90°,∠BAF+∠AFB=90°,
∴∠BAF=∠CFQ,
∵BF=BM,
∴CF=AM,
又∵∠AMF=180°﹣45°=135°,∠FCQ=90°+45°=135°,
∴∠AMF=∠FCQ,
在△AMF和△FCQ中,
,
∴△AMF≌△FCQ(ASA),
∴AF=FQ;
(2)当BF=时,四边形FCQN为平行四边形,
证明:如图,在AB上截取BM=BF,连接MF,
∵BF=,BC=1,
∴FC=,
由(1)可得△BMF为等腰三角形,且△AMF≌△FCQ,
∴CQ=MF=,
∵NQ∥BC,
∴∠FCQ+∠NQC=180°,
∵∠FCQ=135°,
∴∠NQC=45°,
∵∠NCQ=90°,
∴∠NQC=45°=∠NQC,
∴,,
∴NQ=FC且NQ∥FC,
∴四边形FCQN为平行四边形.
19.证明:(1)∵四边形ABCD是正方形,
∴∠DAB=90°,AC平分∠DAB,
∵PM⊥AD,PN⊥AB,
∴∠PMA=∠PNA=90°,
∴四边形MANP是矩形,
∵AC平分∠DAB,PM⊥AD,PN⊥AB,
∴PM=PN,
∴四边形MANP是正方形;
(2)∵四边形ABCD是正方形,
∴PM=PN,∠MPN=90°,
∵∠EPB=90°,
∴∠MPE+∠EPN=∠NPB+∠EPN=90°,
∴∠MPE=∠NPB,
在△EPM和△BPN中,
∵,
∴△EPM≌△BPN(ASA),
∴EM=BN.
20.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.下列关于 ABCD的叙述,正确的是( )
A.若AC=BD,则 ABCD是矩形 B.若AB=AD,则 ABCD是正方形
C.若AB⊥BC,则 ABCD是菱形 D.若AC⊥BD,则 ABCD是正方形
2.如图,正方形ABCD的面积为4,菱形AECF的面积为2,则EF的长是( )
A.1 B. C.2 D.2
3.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
4.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=6,F为DE的中点.若OF的长为1,则△CEF的周长为( )
A.14 B.16 C.18 D.12
5.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2 B.3 C. D.
6.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣2,0),B(2,b),则正方形ABCD的面积是( )
A.34 B.25 C.20 D.16
7.如图,正方形ABCD的边长为2,E为AB边的中点,点F在BC边上,点B关于直线EF的对称点记为B',连接B'D,B'E,B'F.当点F在BC边上移动使得四边形BEB'F成为正方形时,B'D的长为( )
A. B. C.2 D.3
8.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:①AP=EF;②∠PFE=∠BAP;③PD=EC;④△APD一定是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题,满分35分)
9.用4张全等的直角三角形纸片拼接成如图所示的图案,得到两个大小不同的正方形.若正方形ABCD的面积为10,AH=3,则正方形EFGH的面积为 .
10.已知:如图,正方形ABCD和EFGH的边长都等于1,点E恰好是AC、BD的交点,则两个正方形的重叠部分(阴影部分)的面积是 .
11.如图,点A,B,E在同一条直线上,正方形ABCD,BEFG的边长分别为3,4,H为线段DF的中点,则BH= .
12.如图,点O是正方形ABCD的中心,过点O的直线与AD、BC交于点M、点N,DE⊥MN,交AB于点E,若AM=1,DM=3,则DE的长为 .
13.如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是 .
14.如图,在边长为2的正方形ABCD中,E,F分别是边DC,CB上的动点,且始终满足DE=CF,AE,DF交于点P,则∠APD的度数为 ;连接CP,线段CP的最小值为 .
15.如图,在矩形ABCD中,AB=6,BC=8.
(1)如果E、F分别是AD、BC的中点,G是对角线AC上的点,∠EGF=90°,则AG的长为 ;
(2)如果E、F分别是AD、BC上的点,G,H是对角线AC上的点.
下列判断正确的是 .
①在AC上存在无数组G,H,使得四边形EGFH是平行四边形;
②在AC上存在无数组G,H,使得四边形EGFH是矩形;
③在AC上存在无数组G,H,使得四边形EGFH是菱形;
④当AG=时,存在E、F、H,使得四边形EGFH是正方形.
三.解答题(共5小题,满分45分)
16.如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
17.如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
18.在正方形ABCD中,F是线段BC上一动点(不与点B,C重合)连接AF,AC,分别过点F,C作AF、AC的垂线交于点Q.
(1)依题意补全图1,并证明AF=FQ;
(2)过点Q作NQ∥BC,交AC于点N,连接FN.若正方形ABCD的边长为1,写出一个BF的值,使四边形FCQN为平行四边形,并证明.
19.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
20.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵ ABCD中,AC=BD,
∴四边形ABCD是矩形,选项A符合题意;
∵ ABCD中,AB=AD,
∴四边形ABCD是菱形,不一定是正方形,选项B不符合题意;
∵ ABCD中,AB⊥BC,
∴四边形ABCD是矩形,不一定是菱形,选项C不符合题意;
∵ ABCD中,AC⊥BD,
∴四边形ABCD是菱形,选项D不符合题意;
故选:A.
2.解:连接AC,
∵正方形ABCD的面积为4,
∴AC2=4,
解得AC=,
∵菱形AECF的面积为2,
∴AC EF=2,
即×EF=2,
解得EF=,
故选:B.
3.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
4.解:在正方形ABCD中,BO=DO,BC=CD,∠BCD=90°,
∵F为DE的中点,
∴OF为△DBE的中位线,ED=2CF=2EF,
∴△CEF的周长为EF+EC+FC=ED+EC,
∵OF=1,
∴BE=2OF=2,
∵CE=6,
∴BC=BE+CE=2+6=8,
∴CD=BC=8,
在Rt△CED中,∠ECD=90°,CD=8,CE=6,
∴ED=,
∴△CEF的周长为EF+EC+FC=ED+EC=10+6=16,
故选:B.
5.解:过B点作BF⊥CD,与DC的延长线交于F点,
则有△BCF≌△BAE(ASA),
则BE=BF,S四边形ABCD=S正方形BEDF=8,
∴BE==.
故选:C.
6.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣2,0),B(2,b),
∴OA=2,OM=2,
∴OD=AM=4,
∴AD===2,
∴正方形ABCD的面积=2×2=20,
故选:C.
7.解:如图,连接BB',连接BD,
∵四边形ABCD是正方形,
∴BD=AB=2,BD平分∠ABC,
∵E为AB边的中点,
∴AE=BE=1,
∵四边形BEB'F是正方形,
∴BB'=BE=,BB'平分∠ABC,
∴点B,点B',点D三点共线,
∴B'D=BD﹣BB'=,
故选:A.
8.解:作PH⊥AB于H,
∴∠PHB=90°,
∵PE⊥BC,PF⊥CD,
∴∠PEB=∠PEC=∠PFC=90°.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠1=∠2=∠BDC=45°,∠ABC=∠C=90°,
∴四边形BEPH和四边形PECF是矩形,PE=BE,DF=PF,
∴四边形BEPH为正方形,
∴BH=BE=PE=HP,
∴AH=CE,
∴△AHP≌△FPE,
∴AP=EF,∠PFE=∠BAP,
故①、②正确,
在Rt△PDF中,由勾股定理,得
PD=PF,
∴PD=CE.
故③正确.
∵点P在BD上,
∴当AP=AD、PA=PD或DA=DP时△APD是等腰三角形.
∴△APD是等腰三角形只有三种情况.
故④错误,
∴正确的个数有3个.
故选:C.
二.填空题(共7小题,满分35分)
9.解:∵正方形ABCD的面积为10,
∴AD2=10,
∴DH===1,
∵△AHD≌△DGC,
∴AH=DG=3,
∴HG=DG﹣DH=2,
∴正方形EFGH的面积=HG2=4,
故答案为:4.
10.解:∵四边形ABCD是正方形,
∴EC=ED,∠DEC=90°,
∵四边形EFGH是正方形,
∴∠FEH=90°,
∴∠OEC=∠MED,
在△OEC和△MED中,
,
∴△OEC≌△MED(ASA)
∴两个正方形的重叠部分(阴影部分)的面积=△DEC的面积=×正方形ABCD的面积=0.25,故答案为:0.25.
11.解:连接BD、BF,
∵四边形ABCD,BEFG是正方形,且边长分别为3和4,
∴∠DBC=∠GBF=45°,BD=3,BF=4,
∴∠DBF=90°,
由勾股定理得:DF==5,
∵H为线段DF的中点,
∴BH=DF=.
故答案为:.
12.解:如图,连接AC,过点A作AF∥MN,交BC于F,
∵AM=1,DM=3,
∴AD=4,
∵点O是正方形ABCD的中心,
∴AO=CO,AB=AD=BC=4,∠ABC=∠BAD=90°,AD∥BC,
∴∠MAO=∠NCO,
又∵∠AOM=∠CON,AO=CO,
∴△AMO≌△CNO(ASA),
∴AM=CN=1,
∵AD∥BC,AF∥MN,
∴四边形AMNF是平行四边形,
∴AM=FN=1,
∴BF=2,
∵DE⊥MN,AF∥MN,
∴DE⊥AF,
∴∠AED+∠EAF=90°,
又∵∠EAF+∠AFB=90°,
∴∠AED=∠AFB,
又∵∠EAD=∠ABF=90°,AD=AB,
∴△ADE≌△BAF(AAS),
∴AE=BF=2,
∴DE===2,
故答案为2.
13.解:∵AE=BF=CM=DN,
∴AN=DM=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEN≌△DMN≌△CFM≌△BEF.
∴EF=EN=NM=MF,∠ENA=∠DMN.
∴四边形EFMN是菱形.
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,
∴∠ENA+∠DNM=90°.
∴∠ENM=90°.
∴四边形EFMN是正方形,
∴EN最小时,正方形EFMN的面积最小,设AE=DN=x,
则EN==,
∴x=2时,EN的值最小,最小值=,
∴正方形EFMN的面积=()2=8.
14.解:∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠DCF=90°,
在△ADE和△DCF中,
,
∴△ADE≌△DCF(SAS),
∴∠DAE=∠CDF,
∵∠CDF+∠ADF=∠ADC=90°,
∴∠ADF+∠DAE=90°,
∴∠APD=90°,
取AD的中点O,连接OP,则OP=AD=×2=1(不变),
根据两点之间线段最短得C、P、O三点共线时线段CP的值最小,
在Rt△COD中,根据勾股定理得,CO===,
所以,CP=CO﹣OP=﹣1.
故答案为:90°,﹣1.
15.解:(1)如图,
∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,AD=BC,
∴AC===10,
∵AD∥BC,
∴∠EAO=∠FCO,
∵E、F分别是AD、BC的中点,
∴AE=CF=BF=DE,
∴四边形ABFE是平行四边形,
∴EF=AB=6,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(AAS),
∴EO=FO=3,AO=CO=5,
当点G在点O上方时,∵∠EGF=90°,EO=FO,
∴GO=EO=3,
∴AG=AO﹣GO=5﹣3=2,
当点G'在点O下方时,∵∠EG'F=90°,EO=FO,
∴G'O=EO=3,
∴AG'=AO+G'O=5+3=8,
综上所述:AG=2或8;
(2)①在AC上存在无数组G,H,使得四边形EGFH是平行四边形,故该说法正确;
②在AC上存在无数组G,H,使得四边形EGFH是矩形,故该说法正确;
③在AC上存在无数组G,H,使得四边形EGFH是菱形,故该说法正确;
④当AG=时,存在E、F、H,使得四边形EGFH是正方形,
故答案为①②③④.
三.解答题(共5小题,满分45分)
16.(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)判断∠PED=45°.
证明:∵四边形ABCD是正方形,
∴∠BCD=90°,
∵△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
在四边形PECD中,∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴∠PED=45°.
17.解:过B作DA的垂线交DA的延长线于M,M为垂足,
延长DM到G,使MG=CE,连接BG,
易知四边形BCDM是正方形,
则△BEC与△BGM中,
,
∴△BEC≌△BMG(SAS),
∴∠MBG=∠CBE,BE=BG,
∵∠ABE=45°,
∴∠CBE+∠ABM=∠MBG+∠ABM=45°,
即∠ABE=∠ABG=45°,
在△ABE与△ABG中,
,
∴△ABE≌△ABG(SAS),
∴AG=AE=10,
设CE=x,则AM=10﹣x,
AD=12﹣(10﹣x)=2+x,DE=12﹣x,
在Rt△ADE中,AE2=AD2+DE2,
∴100=(x+2)2+(12﹣x)2,
即x2﹣10x+24=0;
解得:x1=4,x2=6.
故CE的长为4或6.
18.解:(1)根据题意,作图如下:
证明:在AB上截取BM=BF,如下图,
∵∠CFQ+∠AFB=90°,∠BAF+∠AFB=90°,
∴∠BAF=∠CFQ,
∵BF=BM,
∴CF=AM,
又∵∠AMF=180°﹣45°=135°,∠FCQ=90°+45°=135°,
∴∠AMF=∠FCQ,
在△AMF和△FCQ中,
,
∴△AMF≌△FCQ(ASA),
∴AF=FQ;
(2)当BF=时,四边形FCQN为平行四边形,
证明:如图,在AB上截取BM=BF,连接MF,
∵BF=,BC=1,
∴FC=,
由(1)可得△BMF为等腰三角形,且△AMF≌△FCQ,
∴CQ=MF=,
∵NQ∥BC,
∴∠FCQ+∠NQC=180°,
∵∠FCQ=135°,
∴∠NQC=45°,
∵∠NCQ=90°,
∴∠NQC=45°=∠NQC,
∴,,
∴NQ=FC且NQ∥FC,
∴四边形FCQN为平行四边形.
19.证明:(1)∵四边形ABCD是正方形,
∴∠DAB=90°,AC平分∠DAB,
∵PM⊥AD,PN⊥AB,
∴∠PMA=∠PNA=90°,
∴四边形MANP是矩形,
∵AC平分∠DAB,PM⊥AD,PN⊥AB,
∴PM=PN,
∴四边形MANP是正方形;
(2)∵四边形ABCD是正方形,
∴PM=PN,∠MPN=90°,
∵∠EPB=90°,
∴∠MPE+∠EPN=∠NPB+∠EPN=90°,
∴∠MPE=∠NPB,
在△EPM和△BPN中,
∵,
∴△EPM≌△BPN(ASA),
∴EM=BN.
20.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
