2021-2022学年人教版九年级数学下册第二十七章相似同步测试卷(一)(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十七章相似同步测试卷(一)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 735.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 22:50:32 | ||
图片预览


文档简介
2022年度初中数学九年级下册第二十七章相似同步测试(一)
一、单选题
1.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB//CD,AB=2米,CD=5米,点P到CD的距离是4米,则P到AB的距离为( )
A.2.5米 B.1.6米 C.1.5米 D.1.2 米
2.已知,那么下列等式中成立的是( )
A. B. C. D..
3.如图,菱形ABCD的边BC在x轴上,点D的坐标为(5,4),分别以A、B为圆心,大于画弧,作直线GF经过弧的交点且分别与边AB,AD交于点E,F,则点F的坐标为( )
A.(4,4) B. C. D.(3,4)
4.如图,在平面直角坐标系中,函数的图象经过菱形的顶点和边的中点,若菱形的边长为6,则的值为( )
A. B. C. D.
5.如图,P为线段AB上的一点,分别以AP、PB为边在AB的同侧作菱形APCD和菱形PBFE,点P、E、C在一条直线上,,,,若EF平分,则为( )
A. B.
C. D.
6.如图,点 D,E 分别在△ABC 的边 AB,AC 上,且满足△ADE∽△ACB, AED B , 若 AB=10,AC=8,AD=4,则 CE 的长是( )
A.2 B.3 C.4 D.5
7.如图,在△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于点E.若AB=4,则CE的长度为( )
A.2 B.2﹣2 C.2+2 D.6﹣2
8.如图,E是矩形ABCD的边AD的中点,连接BE,BD,分别交对角线AC于点F,O.则AF:FO:OC=( )
A.2:1:3 B.3:2:5 C.4:2:7 D.5:3:8
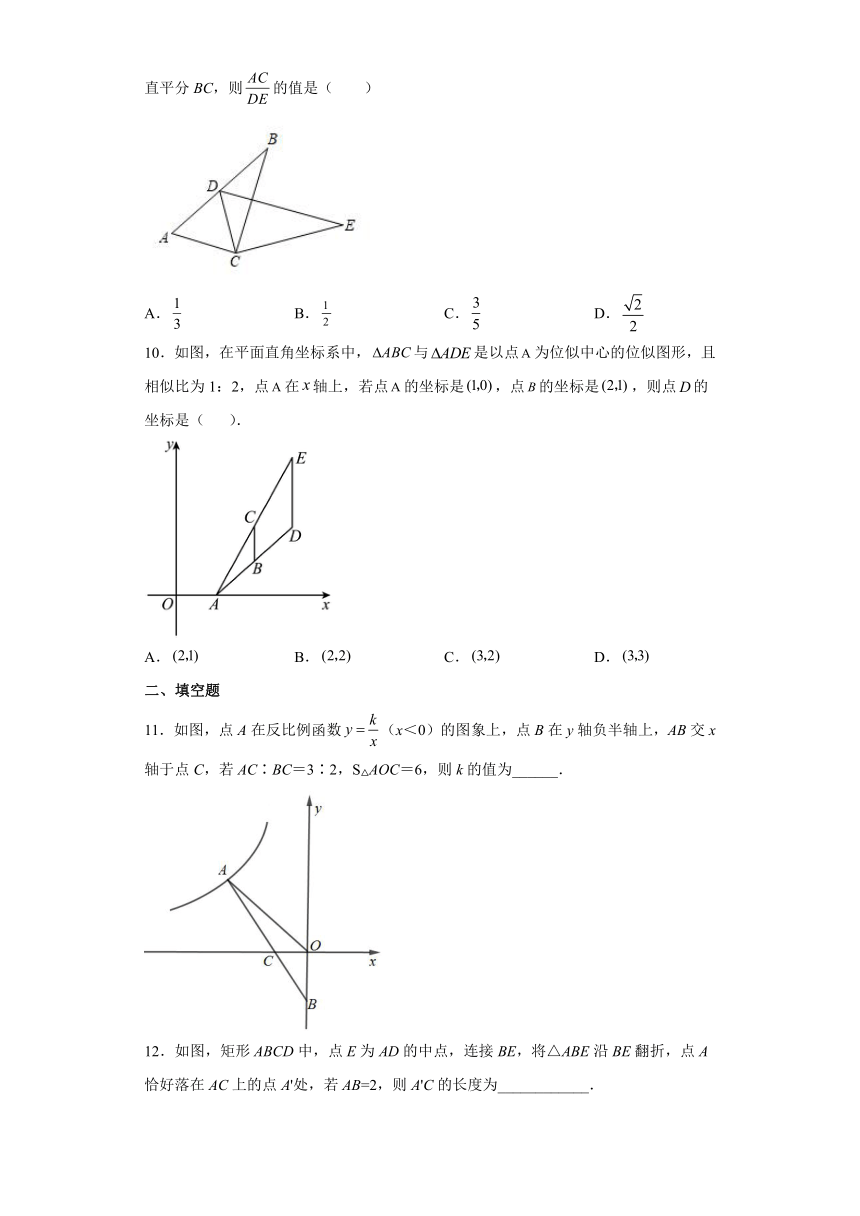
9.如图,将△ABC绕点C顺时针旋转α得到△DEC,此时点D落在边AB上,且DE垂直平分BC,则的值是( )
A. B. C. D.
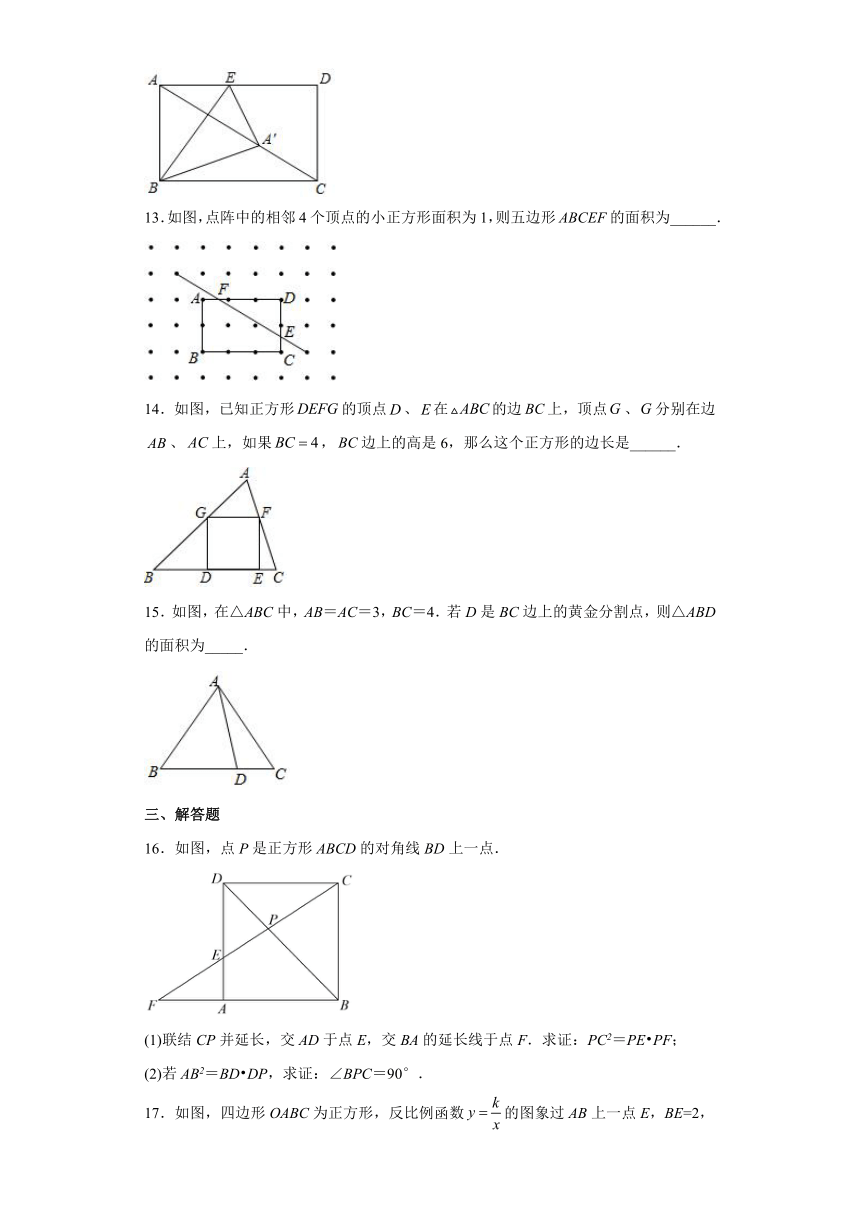
10.如图,在平面直角坐标系中,与是以点为位似中心的位似图形,且相似比为1:2,点在轴上,若点的坐标是,点的坐标是,则点的坐标是( ).
A. B. C. D.
二、填空题
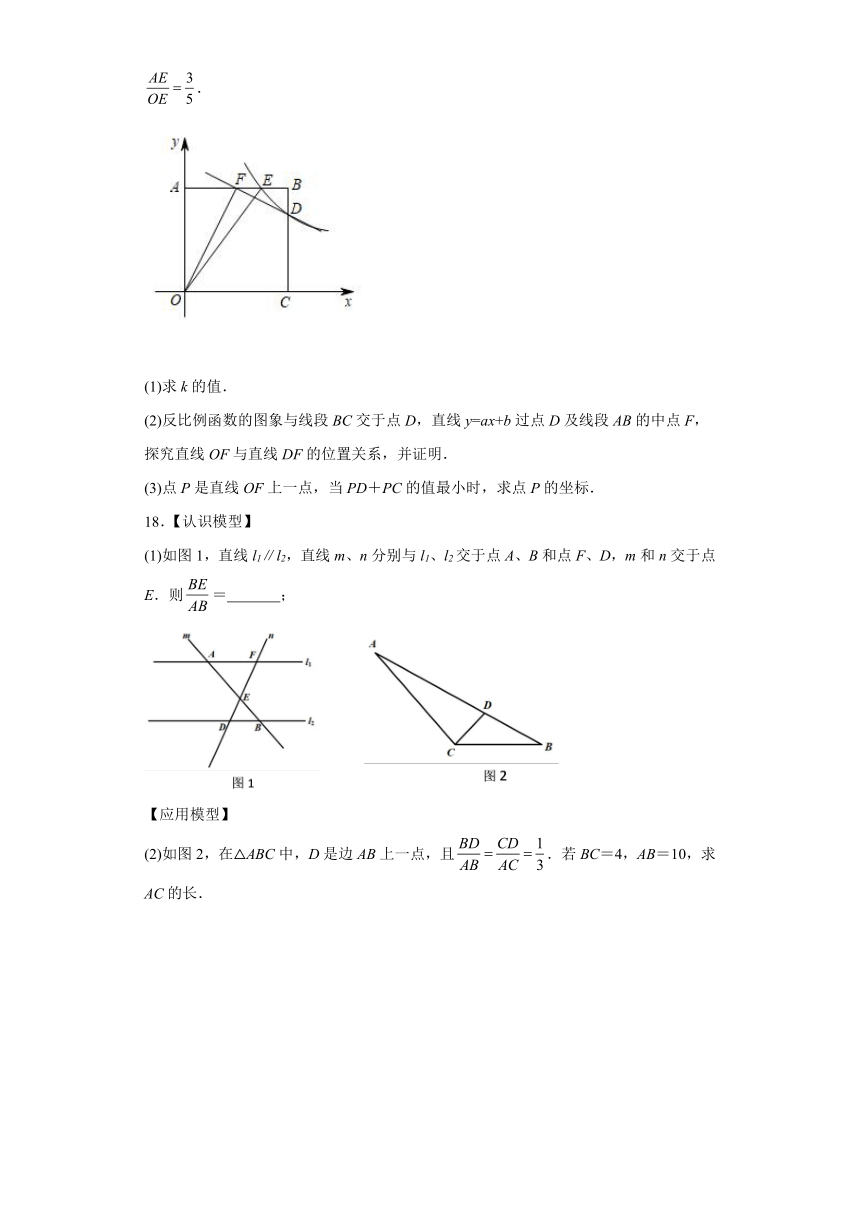
11.如图,点A在反比例函数(x<0)的图象上,点B在y轴负半轴上,AB交x轴于点C,若AC∶BC=3∶2,S△AOC=6,则k的值为______.
12.如图,矩形ABCD中,点E为AD的中点,连接BE,将△ABE沿BE翻折,点A恰好落在AC上的点A'处,若AB=2,则A'C的长度为____________.
13.如图,点阵中的相邻4个顶点的小正方形面积为1,则五边形ABCEF的面积为______.
14.如图,已知正方形的顶点、在的边上,顶点、分别在边、上,如果,边上的高是6,那么这个正方形的边长是______.
15.如图,在△ABC中,AB=AC=3,BC=4.若D是BC边上的黄金分割点,则△ABD的面积为_____.
三、解答题
16.如图,点P是正方形ABCD的对角线BD上一点.
(1)联结CP并延长,交AD于点E,交BA的延长线于点F.求证:PC2=PE PF;
(2)若AB2=BD DP,求证:∠BPC=90°.
17.如图,四边形OABC为正方形,反比例函数的图象过AB上一点E,BE=2,.
(1)求k的值.
(2)反比例函数的图象与线段BC交于点D,直线y=ax+b过点D及线段AB的中点F,探究直线OF与直线DF的位置关系,并证明.
(3)点P是直线OF上一点,当PD+PC的值最小时,求点P的坐标.
18.【认识模型】
(1)如图1,直线l1∥l2,直线m、n分别与l1、l2交于点A、B和点F、D,m和n交于点E.则= ;
【应用模型】
(2)如图2,在△ABC中,D是边AB上一点,且.若BC=4,AB=10,求AC的长.
试卷第1页,共3页
参考答案:
1.B
【详解】
如图,过点P作,分别交AB于点F,交CD于点E
∵AB//CD
∴
∴
又∵AB//CD
∴,
∴
∴
∵,
∴
∴
∴米
故选:B.
2.C
【详解】
解:∵a:b=2:3的两内项是b、2,两外项是a、3,
∴3a=2b,
A:由以上解释易知A选项错误,不符题意;
B:,即,故错误,不符题意;
C: ,即,故正确,符合题意;
D:,即3a=4b,故错误,不符题意;
故选C.
3.B
【详解】
解:由题意知,,EF是AB的垂直平分线,
∴,,,
在中,由勾股定理得,
∵,,
∴,
∴,
∴,
,
解得,
∴,
故选:B.
4.D
【详解】
解:如图,过点、分别作轴的垂线,垂足为、
则∠DMO=∠ENA=90°
∵是菱形
∴,
∴
∴
∴
又
∴设点坐标为,则,
∴
∴点坐标为
又点、都在函数的图象上
∴
解得:
在中,由勾股定理得
∴
故选:D.
5.D
【详解】
解:过点F作,交AB延长线于N,
∵四边形APCD、PBFE是菱形,
∴BF,
∴∠FBN=∠CPB=,
∵四边形PBFE是菱形,
∴PB=PE,
∴∠PBE=∠PEB =,
∴∠N=∠PBE ==∠FBN,△PBE是等边三角形,
∴△BFN是等边三角形,
∴BN=FN=BF=b,
∵EF平分,
∴∠EFC=∠EFM,
∵EF=EF,∠BEF=∠FEC=,
∴△CEF≌△MEF,
∴EM=CE=a-b,
∵BE=PB=b,
∴BM=BE-EM=2b-a,
∵,
∴△ABM∽△ANF,
∴,
∴,
得
∴,
∵a>0,
∴,
∴=,
故选:D.
6.B
【详解】
解:∵△ADE∽△ACB, AED B ,
∴AB:AE=AC:AD,
而AB=10,AC=8,AD=4
∴10:AE=8:4,
∴AE=5
∴ .
故选:B.
7.D
【详解】
∵AB=AC=4,∠C=72°,
∴∠ABC=∠C=72°,
∴∠A=180°﹣∠C﹣∠ABC=36°,
∵AB的垂直平分线DE交AC于点E,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠CBE=∠ABC﹣∠ABE=36°,
∴∠CBE=∠A,
∵∠C=∠C,
∴△CBE∽△CAB,
∴CE:CB=CB:CA,
∵∠CEB=∠A+∠ABE=72°,
∴∠CEB=∠C,
∴BC=BE=AE,
∴CE:AE=AE:CA,
∴点E是线段AC的黄金分割点,且AE>CE,
∴,
∴,
故选:D.
8.A
【详解】
∵四边形ABCD是矩形,
∴AD//BC,AD=BC,OA=OC=AC,
∴△AEF∽△CBF,
∵E是AD的中点,
∴AE=AD,
∴,
∴AF=AC,
∴OF=OA-AF=AC-AC=AC,
∴AF:FO:OC=AC:AC:AC=2:1:3,
故选:A.
9.B
【详解】
解:如图,设与交于点,
由旋转可知:,,,,
垂直平分,
,,,
,
,
,
,
,
,
.
故选:B.
10.C
【详解】
解:过点作垂直于轴的线交于点,如下图:
,
,
,
与是以点为位似中心的位似图形,且相似比为1:2,
,
,
,
,
,
,
,
点的坐标为,
故选:C.
11.
【详解】
解:过点作轴于,
,
在和中,
,
,
,
,S△AOC=6,
,
,
,
,
根据反比例函数的几何意义得,
,
,
.
故答案为:.
12.##
【详解】
解:如图,连接A'D,设BE与AC交于点M,
由翻折知,BE垂直平分AA',
∴AB=A'B=2,AM=A'M,AE=A'E,
∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,∠ABC=90°,
∴∠DCA=∠BAC,
∵点E为AD的中点,
∴AE=DE=A'E,
∴点A,A',D三点在以AD为直径的圆上,
∴∠DA'A=∠DA'C=90°=∠AMB,
∴△ABM≌△CDA'(AAS),
∴A'C=AM,
∴AM=A'M=A'C,
∵∠ABC=∠ANB=90°,∠BAM=∠BAM,
∴△BAM∽△CAB,
∴,
设AM=A'M=A'C=x,则AC=3x,
∴,
解得,x=(取正值),
即A'C=,
故答案为:.
13.
【详解】
解:如图所示:
∵GD∥QH,
∴△PGF∽△PQH,
∴,
,
,
∵CD∥PQ,
∴△HCE∽△HQP,
,
,
∴五边形ABCEF的面积=S△PQH-S△PGF-S△HCE-S矩形ABQG
,
故答案为:.
14.
【详解】
解:作AH⊥BC于H,交GF于M,如图,
设正方形DEFG的边长为x,则GF=x,MH=x,AM=6-x,
∵GF∥BC,
∴△AGF∽△ABC,
∴,即,
解得x=,
即正方形DEFG的边长为.
故答案为:.
15.5﹣或3﹣5
【详解】
解:过作于,如图所示:
,
,
,
的面积,
是边上的黄金分割点,
当时,,
,
的面积;
当时,,
,
,
的面积;
故答案为:或.
16.(1)见解析
(2)见解析
(1)
证明:∵四边形ABCD是正方形,
∴DC∥AB,BC∥AD,
∴△DCP∽△BFP,△DEP∽△BCP,
∴,,
∴,,
∴PC2=PE PF;
(2)
证明:∵四边形ABCD是正方形,
∴AB=CD,∠DCB=90°,
∵
∴DC2=BD DP,
∴,
又∵∠CDP=∠BDC,
∴△CDP∽△BDC,
∴∠DCP=∠BDC,
∴∠DCP+∠CDP=∠CDP+∠DBC=90°,
∴∠DPC=90°,
∴∠BPC=90°.
17.(1)48
(2)OF⊥DF,见解析
(3)
(1)
证明:∵四边形OABC是正方形,
∴AO=AB,∠OAB=90°,
∵,
设AE=3x,则OE=5x,由勾股定理得AO=4x,
∴3x+2=4x,
∴x=2,
∴AE=3x=6,AO=4x=8,
∴点E坐标为(6,8),
∴k=6×8=48;
(2)
解:OF⊥DF,理由如下:
将x=8代入y=得y=6,
∴D(8,6),
∴BD=BC-CD=8-6=2,
∵点F是线段AB的中点,
∴AF=BF=4,
∵,∠OAF=∠FBD=90°,
∴△AOF∽△BFD,
∴∠AOF=∠BFD,
∴∠AFO+∠BFD=∠AFO+∠AOF=90°,
∴∠OFD=180°-(∠AFO+∠BFD)=90°,
∴OF⊥DF;
(3)
(3)延长DF交y轴于点G,连接CG交OF于点P,则点P为所求作点,
∵四边形OABC为正方形,∠AFG=∠BFD,AF=BF,
∴△AFG≌△BFD(AAS),
∴AG=BD=2,GF=DF,
由(2)得OF⊥DF,
∴OF为线段DG的垂直平分线,
∴PD+PC的最小值=PG+PC=CG,
∵OC=OA=8,
∴C(8,0),G(0,10),
设直线CG解析式为y=mx+n,代入C(8,0),G(0,10),
得,解得,
∴
设直线OF为y=ax,代入F(4,8),
∴a=2,
∴y=2x,
联立直线OF、CG得,解得,
∴点P的坐标为(,).
18.(1)
(2)AC=2
(1)
解:∵l1∥l2
(2)
解:如图,过点A作BC的平行线交CD的延长线于点E,作CH⊥AE,垂足为H,交AB于点F.
∵BC∥AE,
∴△CDB∽△EDA ,
=.
∵,
∴AC=CE.
∵=
∴=.
∵△CDB∽△EDA,BC=4,
∴AE=8.
∵AC=CE,CH⊥AE,
∴AH=HE=4.
∴AH=CB,
在△AHF和△BCF中
∴△AHF≌△BCF.
∵AB=10,
∴AF=BF=5.
∴在Rt△AHF中,
∴HC=6.
∴在Rt△ACH中,.
答案第1页,共2页
答案第15页,共16页
一、单选题
1.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB//CD,AB=2米,CD=5米,点P到CD的距离是4米,则P到AB的距离为( )
A.2.5米 B.1.6米 C.1.5米 D.1.2 米
2.已知,那么下列等式中成立的是( )
A. B. C. D..
3.如图,菱形ABCD的边BC在x轴上,点D的坐标为(5,4),分别以A、B为圆心,大于画弧,作直线GF经过弧的交点且分别与边AB,AD交于点E,F,则点F的坐标为( )
A.(4,4) B. C. D.(3,4)
4.如图,在平面直角坐标系中,函数的图象经过菱形的顶点和边的中点,若菱形的边长为6,则的值为( )
A. B. C. D.
5.如图,P为线段AB上的一点,分别以AP、PB为边在AB的同侧作菱形APCD和菱形PBFE,点P、E、C在一条直线上,,,,若EF平分,则为( )
A. B.
C. D.
6.如图,点 D,E 分别在△ABC 的边 AB,AC 上,且满足△ADE∽△ACB, AED B , 若 AB=10,AC=8,AD=4,则 CE 的长是( )
A.2 B.3 C.4 D.5
7.如图,在△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于点E.若AB=4,则CE的长度为( )
A.2 B.2﹣2 C.2+2 D.6﹣2
8.如图,E是矩形ABCD的边AD的中点,连接BE,BD,分别交对角线AC于点F,O.则AF:FO:OC=( )
A.2:1:3 B.3:2:5 C.4:2:7 D.5:3:8
9.如图,将△ABC绕点C顺时针旋转α得到△DEC,此时点D落在边AB上,且DE垂直平分BC,则的值是( )
A. B. C. D.
10.如图,在平面直角坐标系中,与是以点为位似中心的位似图形,且相似比为1:2,点在轴上,若点的坐标是,点的坐标是,则点的坐标是( ).
A. B. C. D.
二、填空题
11.如图,点A在反比例函数(x<0)的图象上,点B在y轴负半轴上,AB交x轴于点C,若AC∶BC=3∶2,S△AOC=6,则k的值为______.
12.如图,矩形ABCD中,点E为AD的中点,连接BE,将△ABE沿BE翻折,点A恰好落在AC上的点A'处,若AB=2,则A'C的长度为____________.
13.如图,点阵中的相邻4个顶点的小正方形面积为1,则五边形ABCEF的面积为______.
14.如图,已知正方形的顶点、在的边上,顶点、分别在边、上,如果,边上的高是6,那么这个正方形的边长是______.
15.如图,在△ABC中,AB=AC=3,BC=4.若D是BC边上的黄金分割点,则△ABD的面积为_____.
三、解答题
16.如图,点P是正方形ABCD的对角线BD上一点.
(1)联结CP并延长,交AD于点E,交BA的延长线于点F.求证:PC2=PE PF;
(2)若AB2=BD DP,求证:∠BPC=90°.
17.如图,四边形OABC为正方形,反比例函数的图象过AB上一点E,BE=2,.
(1)求k的值.
(2)反比例函数的图象与线段BC交于点D,直线y=ax+b过点D及线段AB的中点F,探究直线OF与直线DF的位置关系,并证明.
(3)点P是直线OF上一点,当PD+PC的值最小时,求点P的坐标.
18.【认识模型】
(1)如图1,直线l1∥l2,直线m、n分别与l1、l2交于点A、B和点F、D,m和n交于点E.则= ;
【应用模型】
(2)如图2,在△ABC中,D是边AB上一点,且.若BC=4,AB=10,求AC的长.
试卷第1页,共3页
参考答案:
1.B
【详解】
如图,过点P作,分别交AB于点F,交CD于点E
∵AB//CD
∴
∴
又∵AB//CD
∴,
∴
∴
∵,
∴
∴
∴米
故选:B.
2.C
【详解】
解:∵a:b=2:3的两内项是b、2,两外项是a、3,
∴3a=2b,
A:由以上解释易知A选项错误,不符题意;
B:,即,故错误,不符题意;
C: ,即,故正确,符合题意;
D:,即3a=4b,故错误,不符题意;
故选C.
3.B
【详解】
解:由题意知,,EF是AB的垂直平分线,
∴,,,
在中,由勾股定理得,
∵,,
∴,
∴,
∴,
,
解得,
∴,
故选:B.
4.D
【详解】
解:如图,过点、分别作轴的垂线,垂足为、
则∠DMO=∠ENA=90°
∵是菱形
∴,
∴
∴
∴
又
∴设点坐标为,则,
∴
∴点坐标为
又点、都在函数的图象上
∴
解得:
在中,由勾股定理得
∴
故选:D.
5.D
【详解】
解:过点F作,交AB延长线于N,
∵四边形APCD、PBFE是菱形,
∴BF,
∴∠FBN=∠CPB=,
∵四边形PBFE是菱形,
∴PB=PE,
∴∠PBE=∠PEB =,
∴∠N=∠PBE ==∠FBN,△PBE是等边三角形,
∴△BFN是等边三角形,
∴BN=FN=BF=b,
∵EF平分,
∴∠EFC=∠EFM,
∵EF=EF,∠BEF=∠FEC=,
∴△CEF≌△MEF,
∴EM=CE=a-b,
∵BE=PB=b,
∴BM=BE-EM=2b-a,
∵,
∴△ABM∽△ANF,
∴,
∴,
得
∴,
∵a>0,
∴,
∴=,
故选:D.
6.B
【详解】
解:∵△ADE∽△ACB, AED B ,
∴AB:AE=AC:AD,
而AB=10,AC=8,AD=4
∴10:AE=8:4,
∴AE=5
∴ .
故选:B.
7.D
【详解】
∵AB=AC=4,∠C=72°,
∴∠ABC=∠C=72°,
∴∠A=180°﹣∠C﹣∠ABC=36°,
∵AB的垂直平分线DE交AC于点E,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠CBE=∠ABC﹣∠ABE=36°,
∴∠CBE=∠A,
∵∠C=∠C,
∴△CBE∽△CAB,
∴CE:CB=CB:CA,
∵∠CEB=∠A+∠ABE=72°,
∴∠CEB=∠C,
∴BC=BE=AE,
∴CE:AE=AE:CA,
∴点E是线段AC的黄金分割点,且AE>CE,
∴,
∴,
故选:D.
8.A
【详解】
∵四边形ABCD是矩形,
∴AD//BC,AD=BC,OA=OC=AC,
∴△AEF∽△CBF,
∵E是AD的中点,
∴AE=AD,
∴,
∴AF=AC,
∴OF=OA-AF=AC-AC=AC,
∴AF:FO:OC=AC:AC:AC=2:1:3,
故选:A.
9.B
【详解】
解:如图,设与交于点,
由旋转可知:,,,,
垂直平分,
,,,
,
,
,
,
,
,
.
故选:B.
10.C
【详解】
解:过点作垂直于轴的线交于点,如下图:
,
,
,
与是以点为位似中心的位似图形,且相似比为1:2,
,
,
,
,
,
,
,
点的坐标为,
故选:C.
11.
【详解】
解:过点作轴于,
,
在和中,
,
,
,
,S△AOC=6,
,
,
,
,
根据反比例函数的几何意义得,
,
,
.
故答案为:.
12.##
【详解】
解:如图,连接A'D,设BE与AC交于点M,
由翻折知,BE垂直平分AA',
∴AB=A'B=2,AM=A'M,AE=A'E,
∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,∠ABC=90°,
∴∠DCA=∠BAC,
∵点E为AD的中点,
∴AE=DE=A'E,
∴点A,A',D三点在以AD为直径的圆上,
∴∠DA'A=∠DA'C=90°=∠AMB,
∴△ABM≌△CDA'(AAS),
∴A'C=AM,
∴AM=A'M=A'C,
∵∠ABC=∠ANB=90°,∠BAM=∠BAM,
∴△BAM∽△CAB,
∴,
设AM=A'M=A'C=x,则AC=3x,
∴,
解得,x=(取正值),
即A'C=,
故答案为:.
13.
【详解】
解:如图所示:
∵GD∥QH,
∴△PGF∽△PQH,
∴,
,
,
∵CD∥PQ,
∴△HCE∽△HQP,
,
,
∴五边形ABCEF的面积=S△PQH-S△PGF-S△HCE-S矩形ABQG
,
故答案为:.
14.
【详解】
解:作AH⊥BC于H,交GF于M,如图,
设正方形DEFG的边长为x,则GF=x,MH=x,AM=6-x,
∵GF∥BC,
∴△AGF∽△ABC,
∴,即,
解得x=,
即正方形DEFG的边长为.
故答案为:.
15.5﹣或3﹣5
【详解】
解:过作于,如图所示:
,
,
,
的面积,
是边上的黄金分割点,
当时,,
,
的面积;
当时,,
,
,
的面积;
故答案为:或.
16.(1)见解析
(2)见解析
(1)
证明:∵四边形ABCD是正方形,
∴DC∥AB,BC∥AD,
∴△DCP∽△BFP,△DEP∽△BCP,
∴,,
∴,,
∴PC2=PE PF;
(2)
证明:∵四边形ABCD是正方形,
∴AB=CD,∠DCB=90°,
∵
∴DC2=BD DP,
∴,
又∵∠CDP=∠BDC,
∴△CDP∽△BDC,
∴∠DCP=∠BDC,
∴∠DCP+∠CDP=∠CDP+∠DBC=90°,
∴∠DPC=90°,
∴∠BPC=90°.
17.(1)48
(2)OF⊥DF,见解析
(3)
(1)
证明:∵四边形OABC是正方形,
∴AO=AB,∠OAB=90°,
∵,
设AE=3x,则OE=5x,由勾股定理得AO=4x,
∴3x+2=4x,
∴x=2,
∴AE=3x=6,AO=4x=8,
∴点E坐标为(6,8),
∴k=6×8=48;
(2)
解:OF⊥DF,理由如下:
将x=8代入y=得y=6,
∴D(8,6),
∴BD=BC-CD=8-6=2,
∵点F是线段AB的中点,
∴AF=BF=4,
∵,∠OAF=∠FBD=90°,
∴△AOF∽△BFD,
∴∠AOF=∠BFD,
∴∠AFO+∠BFD=∠AFO+∠AOF=90°,
∴∠OFD=180°-(∠AFO+∠BFD)=90°,
∴OF⊥DF;
(3)
(3)延长DF交y轴于点G,连接CG交OF于点P,则点P为所求作点,
∵四边形OABC为正方形,∠AFG=∠BFD,AF=BF,
∴△AFG≌△BFD(AAS),
∴AG=BD=2,GF=DF,
由(2)得OF⊥DF,
∴OF为线段DG的垂直平分线,
∴PD+PC的最小值=PG+PC=CG,
∵OC=OA=8,
∴C(8,0),G(0,10),
设直线CG解析式为y=mx+n,代入C(8,0),G(0,10),
得,解得,
∴
设直线OF为y=ax,代入F(4,8),
∴a=2,
∴y=2x,
联立直线OF、CG得,解得,
∴点P的坐标为(,).
18.(1)
(2)AC=2
(1)
解:∵l1∥l2
(2)
解:如图,过点A作BC的平行线交CD的延长线于点E,作CH⊥AE,垂足为H,交AB于点F.
∵BC∥AE,
∴△CDB∽△EDA ,
=.
∵,
∴AC=CE.
∵=
∴=.
∵△CDB∽△EDA,BC=4,
∴AE=8.
∵AC=CE,CH⊥AE,
∴AH=HE=4.
∴AH=CB,
在△AHF和△BCF中
∴△AHF≌△BCF.
∵AB=10,
∴AF=BF=5.
∴在Rt△AHF中,
∴HC=6.
∴在Rt△ACH中,.
答案第1页,共2页
答案第15页,共16页
