2021-2022学年华东师大版八年级数学下册16.2.2分式的加减同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学下册16.2.2分式的加减同步练习题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 198.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 22:50:30 | ||
图片预览
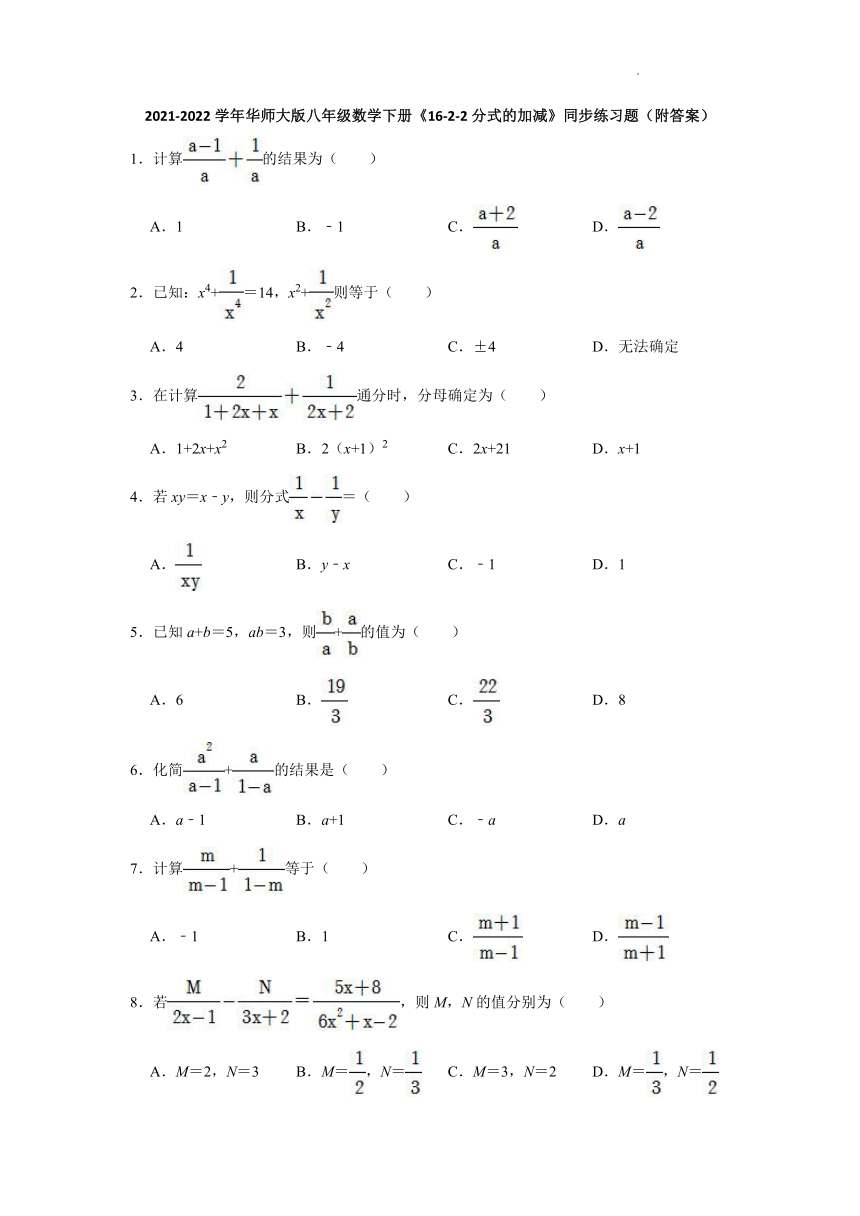
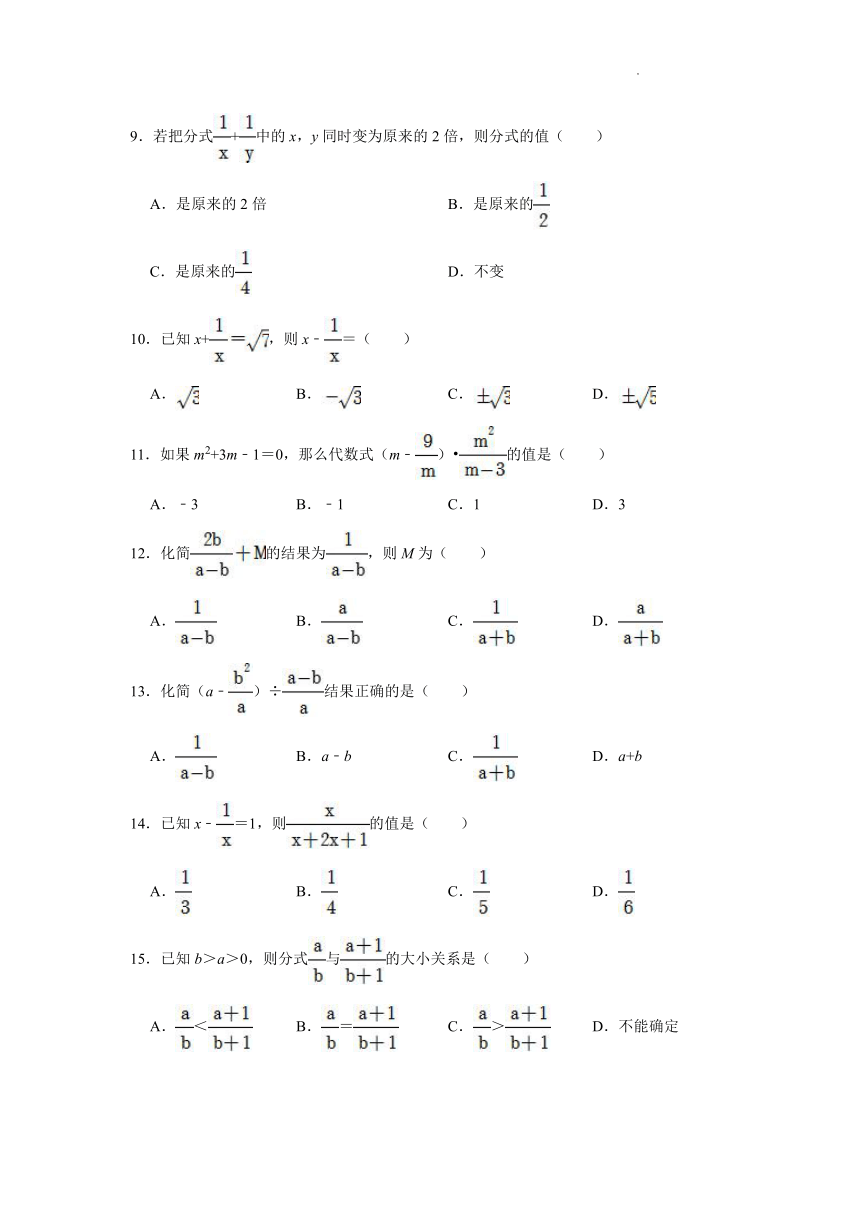

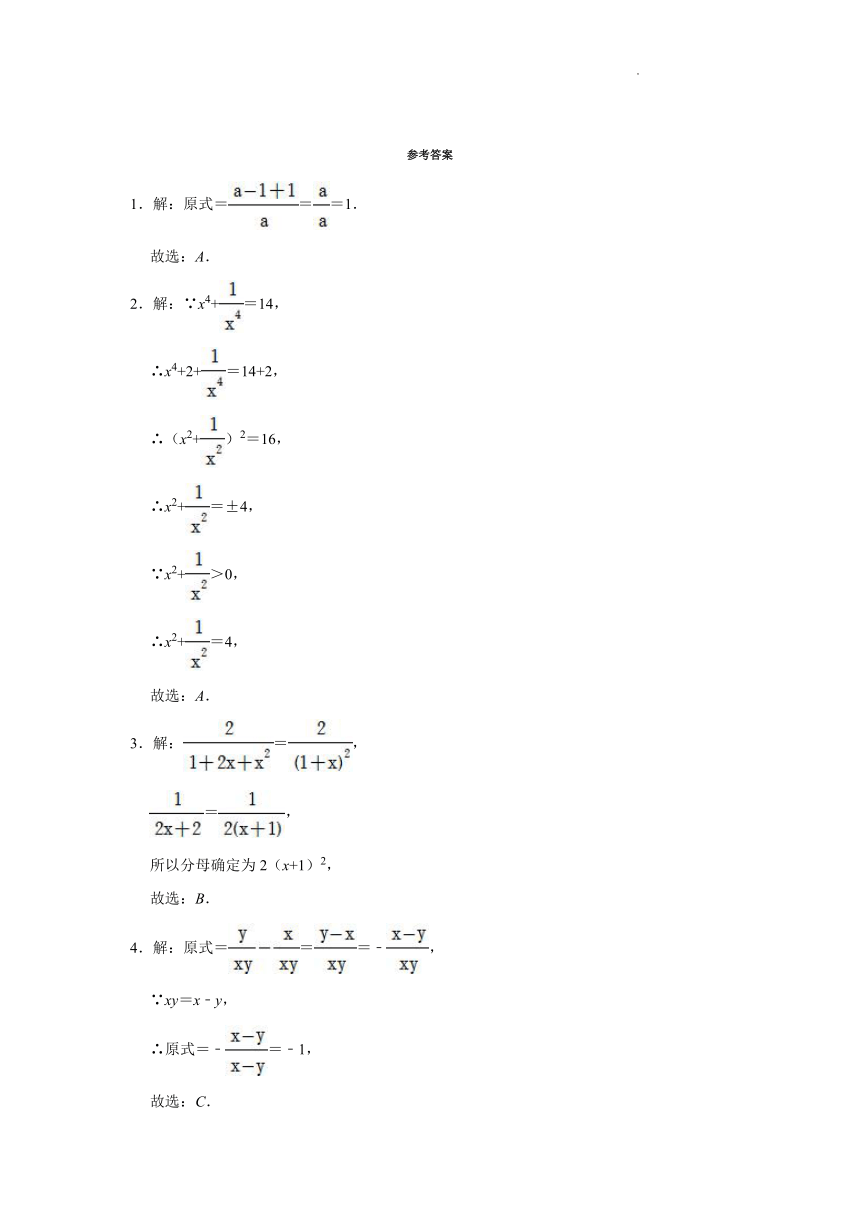

文档简介
2021-2022学年华师大版八年级数学下册《16-2-2分式的加减》同步练习题(附答案)
1.计算的结果为( )
A.1 B.﹣1 C. D.
2.已知:x4+=14,x2+则等于( )
A.4 B.﹣4 C.±4 D.无法确定
3.在计算通分时,分母确定为( )
A.1+2x+x2 B.2(x+1)2 C.2x+21 D.x+1
4.若xy=x﹣y,则分式=( )
A. B.y﹣x C.﹣1 D.1
5.已知a+b=5,ab=3,则+的值为( )
A.6 B. C. D.8
6.化简+的结果是( )
A.a﹣1 B.a+1 C.﹣a D.a
7.计算+等于( )
A.﹣1 B.1 C. D.
8.若,则M,N的值分别为( )
A.M=2,N=3 B.M=,N= C.M=3,N=2 D.M=,N=
9.若把分式+中的x,y同时变为原来的2倍,则分式的值( )
A.是原来的2倍 B.是原来的
C.是原来的 D.不变
10.已知x+,则x﹣=( )
A. B. C. D.
11.如果m2+3m﹣1=0,那么代数式(m﹣) 的值是( )
A.﹣3 B.﹣1 C.1 D.3
12.化简的结果为,则M为( )
A. B. C. D.
13.化简(a﹣)÷结果正确的是( )
A. B.a﹣b C. D.a+b
14.已知x﹣=1,则的值是( )
A. B. C. D.
15.已知b>a>0,则分式与的大小关系是( )
A.< B.= C.> D.不能确定
16.已知x2﹣4x+1=0,则x2+的值是 .
17.计算:= .
18.计算:﹣m= .
19.比较大小:若a,b为实数,且ab=1,设,,则P Q.
20.定义新运算:a b=+,若a (﹣b)=2,则的值是 .
21.计算:
(1)(m+2);
(2)().
22.先化简,再从﹣2,﹣1,0,1,2中选一个合适的整数作为x的值代入求值.
23.已知a2+2a﹣1=0,求代数式()÷的值.
24.若A=(1﹣)÷,先化简A,然后从﹣2≤x≤2中,选择一个合适的整数作为x的值代入A,求出A的值.
参考答案
1.解:原式===1.
故选:A.
2.解:∵x4+=14,
∴x4+2+=14+2,
∴(x2+)2=16,
∴x2+=±4,
∵x2+>0,
∴x2+=4,
故选:A.
3.解:=,
=,
所以分母确定为2(x+1)2,
故选:B.
4.解:原式===﹣,
∵xy=x﹣y,
∴原式=﹣=﹣1,
故选:C.
5.解:∵a+b=5,ab=3,
∴+
=
=
=
=
=,
故选:B.
6.解:+
=﹣
=
=
=a,
故选:D.
7.解:+
=
=
=1,
故选:B.
8.解:∵﹣==,且﹣=,
∴=,即(3M﹣2N)x+(2M+N)=5x+8,
∴3M﹣2N=5,2M+N=8,
解得:M=3,N=2.
故选:C.
9.解:+=,
+
=,
分式的值是原来的,
故选:B.
10.解:∵x+,
∴(x+)2=7,即x2+2+=7,
∴x2+=5,
∴x2﹣2+=3,即(x﹣)2=3,
则x﹣=,
故选:C.
11.解:原式=,
=,
=,
=(m+3)m,
=m2+3m,
∵m2+3m﹣1=0,
∴m2+3m=1,
故选:C.
12.解:由题意得,M=﹣=﹣==.
故选:C.
13.解:原式=(﹣)
=
=
=a+b.
故选:D.
14.解:∵x﹣=1,
∴(x﹣)2=1,
∴x2+=3,
原式的倒数为,
∴原式=,
故选:C.
15.解:∵﹣
=
=,
∵b>a>0,
∴a﹣b<0,b>0,b+1>0,
∴<0,
∴﹣<0,
∴<,
故选:A.
16.解:原式=(x+)2﹣2,
∵x2﹣4x+1=0,且由题意可得x≠0,
∴﹣=0,
∴x+=4,
∴原式=42﹣2=14,
故答案为:14.
17.解:原式=
=
=
=,
故答案为:.
18.解:原式=﹣m=m+1﹣m=1.
19.解:∵ab=1,
∴P=+
=+
=+
=+=Q,
则P=Q.
故答案为:=.
20.解:根据题意可得,
∵a (﹣b)=2,
∴=2,
即=2,
∴b﹣a=2ab,
∴2a﹣2b=2(a﹣b)=﹣4ab,
∴==﹣.
故答案为:﹣.
21.解:(1)原式=[﹣]
=
=
=
=﹣2(m+3)
=﹣2m﹣6.
(2)原式=[﹣]
=
=
=
=.
22.原式=÷+
= +
=+
=
由分式有意义的条件可知:x≠﹣1,1,2,
∴x=0或﹣2,
当x=0时,
原式==﹣1.
23.解:原式=[] a(a﹣1)
=(+) a(a﹣1)
= a(a﹣1)
=a2+2a,
∵a2+2a﹣1=0,
∴a2+2a=1,
∴原式=1.
24.解:A=(﹣)÷
=
=,
∵﹣2≤x≤2,
∴整数x=﹣2,﹣1,0,1,2,
当x=﹣2,﹣1,0时,原式没有意义;
当x=1时,A=;当x=2时,A=.
1.计算的结果为( )
A.1 B.﹣1 C. D.
2.已知:x4+=14,x2+则等于( )
A.4 B.﹣4 C.±4 D.无法确定
3.在计算通分时,分母确定为( )
A.1+2x+x2 B.2(x+1)2 C.2x+21 D.x+1
4.若xy=x﹣y,则分式=( )
A. B.y﹣x C.﹣1 D.1
5.已知a+b=5,ab=3,则+的值为( )
A.6 B. C. D.8
6.化简+的结果是( )
A.a﹣1 B.a+1 C.﹣a D.a
7.计算+等于( )
A.﹣1 B.1 C. D.
8.若,则M,N的值分别为( )
A.M=2,N=3 B.M=,N= C.M=3,N=2 D.M=,N=
9.若把分式+中的x,y同时变为原来的2倍,则分式的值( )
A.是原来的2倍 B.是原来的
C.是原来的 D.不变
10.已知x+,则x﹣=( )
A. B. C. D.
11.如果m2+3m﹣1=0,那么代数式(m﹣) 的值是( )
A.﹣3 B.﹣1 C.1 D.3
12.化简的结果为,则M为( )
A. B. C. D.
13.化简(a﹣)÷结果正确的是( )
A. B.a﹣b C. D.a+b
14.已知x﹣=1,则的值是( )
A. B. C. D.
15.已知b>a>0,则分式与的大小关系是( )
A.< B.= C.> D.不能确定
16.已知x2﹣4x+1=0,则x2+的值是 .
17.计算:= .
18.计算:﹣m= .
19.比较大小:若a,b为实数,且ab=1,设,,则P Q.
20.定义新运算:a b=+,若a (﹣b)=2,则的值是 .
21.计算:
(1)(m+2);
(2)().
22.先化简,再从﹣2,﹣1,0,1,2中选一个合适的整数作为x的值代入求值.
23.已知a2+2a﹣1=0,求代数式()÷的值.
24.若A=(1﹣)÷,先化简A,然后从﹣2≤x≤2中,选择一个合适的整数作为x的值代入A,求出A的值.
参考答案
1.解:原式===1.
故选:A.
2.解:∵x4+=14,
∴x4+2+=14+2,
∴(x2+)2=16,
∴x2+=±4,
∵x2+>0,
∴x2+=4,
故选:A.
3.解:=,
=,
所以分母确定为2(x+1)2,
故选:B.
4.解:原式===﹣,
∵xy=x﹣y,
∴原式=﹣=﹣1,
故选:C.
5.解:∵a+b=5,ab=3,
∴+
=
=
=
=
=,
故选:B.
6.解:+
=﹣
=
=
=a,
故选:D.
7.解:+
=
=
=1,
故选:B.
8.解:∵﹣==,且﹣=,
∴=,即(3M﹣2N)x+(2M+N)=5x+8,
∴3M﹣2N=5,2M+N=8,
解得:M=3,N=2.
故选:C.
9.解:+=,
+
=,
分式的值是原来的,
故选:B.
10.解:∵x+,
∴(x+)2=7,即x2+2+=7,
∴x2+=5,
∴x2﹣2+=3,即(x﹣)2=3,
则x﹣=,
故选:C.
11.解:原式=,
=,
=,
=(m+3)m,
=m2+3m,
∵m2+3m﹣1=0,
∴m2+3m=1,
故选:C.
12.解:由题意得,M=﹣=﹣==.
故选:C.
13.解:原式=(﹣)
=
=
=a+b.
故选:D.
14.解:∵x﹣=1,
∴(x﹣)2=1,
∴x2+=3,
原式的倒数为,
∴原式=,
故选:C.
15.解:∵﹣
=
=,
∵b>a>0,
∴a﹣b<0,b>0,b+1>0,
∴<0,
∴﹣<0,
∴<,
故选:A.
16.解:原式=(x+)2﹣2,
∵x2﹣4x+1=0,且由题意可得x≠0,
∴﹣=0,
∴x+=4,
∴原式=42﹣2=14,
故答案为:14.
17.解:原式=
=
=
=,
故答案为:.
18.解:原式=﹣m=m+1﹣m=1.
19.解:∵ab=1,
∴P=+
=+
=+
=+=Q,
则P=Q.
故答案为:=.
20.解:根据题意可得,
∵a (﹣b)=2,
∴=2,
即=2,
∴b﹣a=2ab,
∴2a﹣2b=2(a﹣b)=﹣4ab,
∴==﹣.
故答案为:﹣.
21.解:(1)原式=[﹣]
=
=
=
=﹣2(m+3)
=﹣2m﹣6.
(2)原式=[﹣]
=
=
=
=.
22.原式=÷+
= +
=+
=
由分式有意义的条件可知:x≠﹣1,1,2,
∴x=0或﹣2,
当x=0时,
原式==﹣1.
23.解:原式=[] a(a﹣1)
=(+) a(a﹣1)
= a(a﹣1)
=a2+2a,
∵a2+2a﹣1=0,
∴a2+2a=1,
∴原式=1.
24.解:A=(﹣)÷
=
=,
∵﹣2≤x≤2,
∴整数x=﹣2,﹣1,0,1,2,
当x=﹣2,﹣1,0时,原式没有意义;
当x=1时,A=;当x=2时,A=.
