2021-2022学年苏科版九年级数学下册6.3相似图形培优训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册6.3相似图形培优训练(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 126.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 22:53:10 | ||
图片预览


文档简介
6.3相似图形
一、选择题
1、两个多边形相似的条件是( )
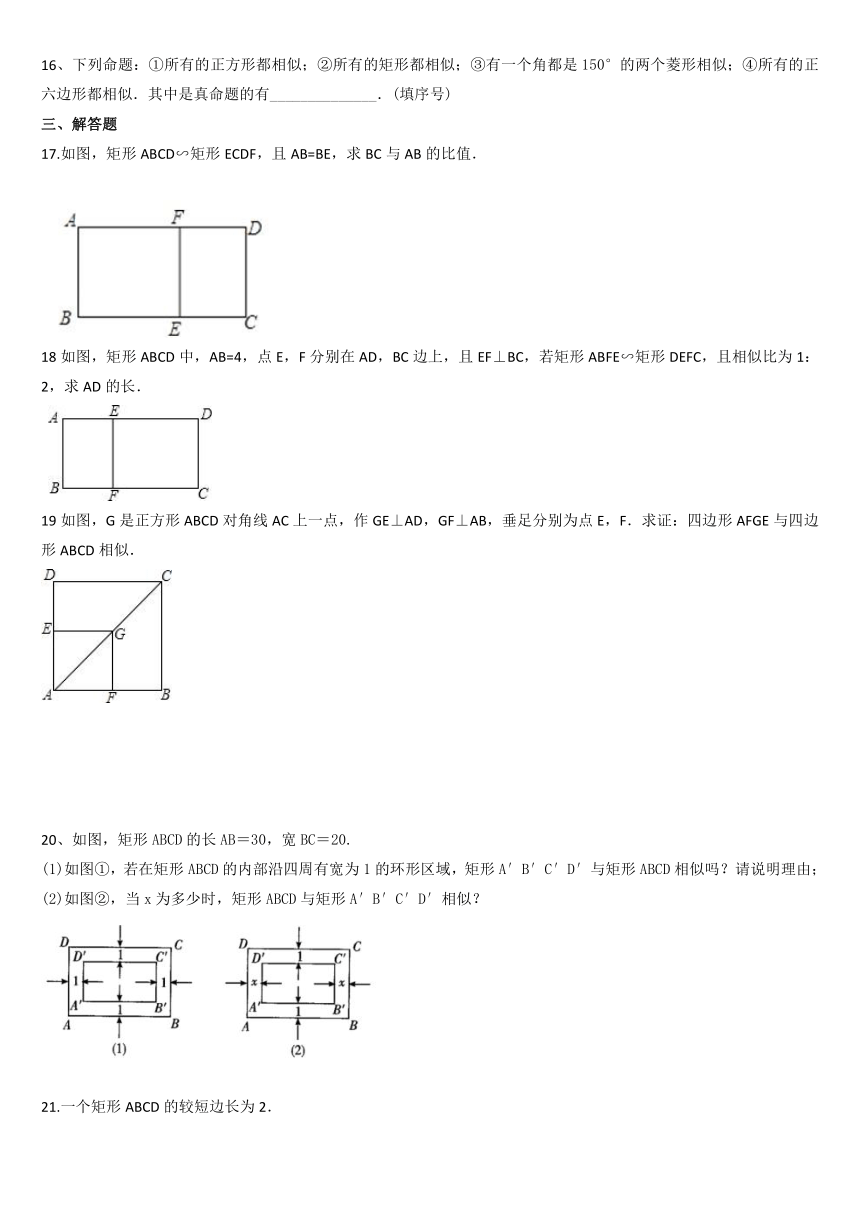
A.对应角相等 B.对应边成比例 C.对应角相等或对应边成比例 D.对应角相等且对应边成比例
2、下列每组中的两个图形形状相同的是( )
3.小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中的对应线段是( )
A. FG B. FH C. EH D. EF
4.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A. 70° B. 80° C. 90° D. 120°
5.把一张矩形的纸片对折后和原矩形相似,那么大矩形与小矩形的相似比是( )
A. :1 B. 4:1 C. 3:1 D. 2:1
6.下面的图形都可以看作某种特殊的“细胞”,它们分裂时能同时分裂为全等的4个小细胞,分裂的小细胞与原图形相似,则相似比为( )
A. 1:4 B. 1:3 C. 1:2 D. 1:
7.如图,矩形ABCD∽矩形BCFE , 且AD=AE.则AB:AD的值是( )
A. B. C. D.
8如图,在长为、宽为的矩形中,截去一个矩形,使得留下的矩形图中阴影部分与原矩形相似,则留下的矩形面积是
A. B. C. D.
9下列说法:有一个锐角相等的两个直角三角形相似;顶角相等的两个等腰三角形相似;任意两个菱形一定相似;位似图形一定是相似图形;其中正确的个数是
A. 1个 B. 2个 C. 3个 D. 4个
10两个五角星相似,相似比为,则它们的面积比等于
A. B. C. D.
二、填空题
11. 给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有________(填序号).
12.两个相似多边形一组对应边分别为3cm,5cm,那么它们的相似比为________.
13.给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有________(填序号).
14.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是________ cm2 .
15.如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为________.
16、下列命题:①所有的正方形都相似;②所有的矩形都相似;③有一个角都是150°的两个菱形相似;④所有的正六边形都相似.其中是真命题的有______________.(填序号)
三、解答题
17.如图,矩形ABCD∽矩形ECDF,且AB=BE,求BC与AB的比值.
18如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.
19如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
20、如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若在矩形ABCD的内部沿四周有宽为1的环形区域,矩形A′B′C′D′与矩形ABCD相似吗?请说明理由;
(2)如图②,当x为多少时,矩形ABCD与矩形A′B′C′D′相似?
21.一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
22一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
(答案)
一、选择题
1、D 2、A 3、D 4、B 5、A 6、C 7、C 8、C 9、C 10、A
二、填空题
11.【答案】①②④⑤
12.【答案】 3:5
13.【答案】 ①②④⑤
14.【答案】 18
15.【答案】
16、______ ① ③ ④________
三、解答题
17.【答案】 解:∵矩形ABCD∽矩形ECDF,∴, 即∴BC2﹣BC AB﹣CD2=0,解得,BC=CD,∵BC、CD是正数,∴
18【答案】 解:∵矩形ABFE∽矩形DEFC,且相似比为1:2,
∴ = = ,
∵四边形ABCD为矩形,
∴CD=AB=4
∴ = = ,
∴DE=8,AE=2,
∴AD=AE+DE=2+8=10
19.【答案】 证明;∵∠GEA=∠EAF=∠GFA=90°,∴四边形EAFG为矩形.∵四边形ABCD为正方形,∴AC平分∠DAB.又∵GE⊥AD,GF⊥AB,∴GE=GF.∴四边形EAFG为正方形.∴四边形AFGE与四边形ABCD相似
20、如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若在矩形ABCD的内部沿四周有宽为1的环形区域,矩形A′B′C′D′与矩形ABCD相似吗?请说明理由;
(2)如图②,当x为多少时,矩形ABCD与矩形A′B′C′D′相似?
解:(1)不相似.理由:由题意,得AB=30,A′B′=28,BC=20,B′C′=18,
而≠,故矩形A′B′C′D′与矩形ABCD不相似.
(2)若矩形ABCD与矩形A′B′C′D′相似,则=或=,
即=或=,解得x=1.5或x=9.
故当x为1.5或9时,矩形ABCD与矩形A′B′C′D′相似.
21.【答案】 (1)解:由已知得MN=AB=2,MD= AD= BC,
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似, = ,
∴DM BC=AB MN,即 BC2=4,
∴BC=2 ,即它的另一边长为2
(2)解:∵矩形EFDC与原矩形ABCD相似,
∴ = ,
∵AB=CD=2,BC=4,
∴DF= =1,
∴矩形EFDC的面积=CD DF=2×1=2
22.【答案】 (1)解:由已知得MN=AB=2,MD= AD= BC,∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似, = ,
∴DM BC=AB MN,即 BC2=4,
∴BC=2 ,即它的另一边长为2
(2)解:∵矩形EFDC与原矩形ABCD相似,
∴ = ,
∵AB=CD=2,BC=4,
∴DF= =1,
∴矩形EFDC的面积=CD DF=2×1=2
一、选择题
1、两个多边形相似的条件是( )
A.对应角相等 B.对应边成比例 C.对应角相等或对应边成比例 D.对应角相等且对应边成比例
2、下列每组中的两个图形形状相同的是( )
3.小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中的对应线段是( )
A. FG B. FH C. EH D. EF
4.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A. 70° B. 80° C. 90° D. 120°
5.把一张矩形的纸片对折后和原矩形相似,那么大矩形与小矩形的相似比是( )
A. :1 B. 4:1 C. 3:1 D. 2:1
6.下面的图形都可以看作某种特殊的“细胞”,它们分裂时能同时分裂为全等的4个小细胞,分裂的小细胞与原图形相似,则相似比为( )
A. 1:4 B. 1:3 C. 1:2 D. 1:
7.如图,矩形ABCD∽矩形BCFE , 且AD=AE.则AB:AD的值是( )
A. B. C. D.
8如图,在长为、宽为的矩形中,截去一个矩形,使得留下的矩形图中阴影部分与原矩形相似,则留下的矩形面积是
A. B. C. D.
9下列说法:有一个锐角相等的两个直角三角形相似;顶角相等的两个等腰三角形相似;任意两个菱形一定相似;位似图形一定是相似图形;其中正确的个数是
A. 1个 B. 2个 C. 3个 D. 4个
10两个五角星相似,相似比为,则它们的面积比等于
A. B. C. D.
二、填空题
11. 给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有________(填序号).
12.两个相似多边形一组对应边分别为3cm,5cm,那么它们的相似比为________.
13.给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有________(填序号).
14.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是________ cm2 .
15.如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为________.
16、下列命题:①所有的正方形都相似;②所有的矩形都相似;③有一个角都是150°的两个菱形相似;④所有的正六边形都相似.其中是真命题的有______________.(填序号)
三、解答题
17.如图,矩形ABCD∽矩形ECDF,且AB=BE,求BC与AB的比值.
18如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.
19如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
20、如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若在矩形ABCD的内部沿四周有宽为1的环形区域,矩形A′B′C′D′与矩形ABCD相似吗?请说明理由;
(2)如图②,当x为多少时,矩形ABCD与矩形A′B′C′D′相似?
21.一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
22一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
(答案)
一、选择题
1、D 2、A 3、D 4、B 5、A 6、C 7、C 8、C 9、C 10、A
二、填空题
11.【答案】①②④⑤
12.【答案】 3:5
13.【答案】 ①②④⑤
14.【答案】 18
15.【答案】
16、______ ① ③ ④________
三、解答题
17.【答案】 解:∵矩形ABCD∽矩形ECDF,∴, 即∴BC2﹣BC AB﹣CD2=0,解得,BC=CD,∵BC、CD是正数,∴
18【答案】 解:∵矩形ABFE∽矩形DEFC,且相似比为1:2,
∴ = = ,
∵四边形ABCD为矩形,
∴CD=AB=4
∴ = = ,
∴DE=8,AE=2,
∴AD=AE+DE=2+8=10
19.【答案】 证明;∵∠GEA=∠EAF=∠GFA=90°,∴四边形EAFG为矩形.∵四边形ABCD为正方形,∴AC平分∠DAB.又∵GE⊥AD,GF⊥AB,∴GE=GF.∴四边形EAFG为正方形.∴四边形AFGE与四边形ABCD相似
20、如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若在矩形ABCD的内部沿四周有宽为1的环形区域,矩形A′B′C′D′与矩形ABCD相似吗?请说明理由;
(2)如图②,当x为多少时,矩形ABCD与矩形A′B′C′D′相似?
解:(1)不相似.理由:由题意,得AB=30,A′B′=28,BC=20,B′C′=18,
而≠,故矩形A′B′C′D′与矩形ABCD不相似.
(2)若矩形ABCD与矩形A′B′C′D′相似,则=或=,
即=或=,解得x=1.5或x=9.
故当x为1.5或9时,矩形ABCD与矩形A′B′C′D′相似.
21.【答案】 (1)解:由已知得MN=AB=2,MD= AD= BC,
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似, = ,
∴DM BC=AB MN,即 BC2=4,
∴BC=2 ,即它的另一边长为2
(2)解:∵矩形EFDC与原矩形ABCD相似,
∴ = ,
∵AB=CD=2,BC=4,
∴DF= =1,
∴矩形EFDC的面积=CD DF=2×1=2
22.【答案】 (1)解:由已知得MN=AB=2,MD= AD= BC,∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似, = ,
∴DM BC=AB MN,即 BC2=4,
∴BC=2 ,即它的另一边长为2
(2)解:∵矩形EFDC与原矩形ABCD相似,
∴ = ,
∵AB=CD=2,BC=4,
∴DF= =1,
∴矩形EFDC的面积=CD DF=2×1=2
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
