5.3.2 函数的极值与最大(小)值同步练习-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(word含解析)
文档属性
| 名称 | 5.3.2 函数的极值与最大(小)值同步练习-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(word含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-05 09:27:37 | ||
图片预览




文档简介
5.3.2 函数的极值与最大(小)值
◎判断函数的极值点与极值
1.(2021·全国·高二课时练习) 如图是f(x)的导函数f′(x)的图象,则f(x)的极小值点的个数为( )
A.1 B.2 C.3 D.4
2.(2021·广西·昭平中学高二阶段练习(理))下列函数中,存在极值的函数为( )
A. B. C. D.
3.(2021·山东·广饶一中练习)已知在上连续,是的导函数,则是为函数极值点的( )条件.
A.充要条件 B.充分不必要 C.必要不充分 D.既不充分也不必要
4.(2022·重庆八中高二期末)(多选)函数的导函数的图象如图所示,则下列说法正确的有( )
A.为函数的一个零点
B.为函数的一个极大值点
C.函数在区间上单调递增
D.是函数的最大值
◎求函数的极值
1.(2022·河南驻马店·期末(文))函数的极小值是______.
2.(2021·广西·钦州一中高二期中(文))已知函数.
(1)求曲线在点处的切线方程;
(2)求函数的单调区间和极值.
◎求函数的最值
1.(2021·全国·专题练习(理))已知函数在处有极值2.
(1)求,的值;
(2)求函数在区间上的最值.
◎含参数问题
1.(2021·江苏·南京市宁海中学高二期中)已知函数在处有极值0,则的值为( )
A.4 B.7 C.11 D.4或11
2.(2021·江苏·高二专题练习)(1)若函数f(x)=ax3+bx-4在x=1处取得极值,且极值为0,求实数a,b的值;
(2)已知函数f(x)=ax3-6ax2+b(a≠0),是否存在实数a,b使f(x)在区间[-1,2]上取得最大值3,最小值-29 若存在,求出a,b的值;若不存在,请说明理由.
3.(2022·全国·高二课时练习)若函数既有极大值又有极小值,则实数a的取值范围是______.
4.(2021·湖北·应城市第一高级中学高三阶段练习)已知方程对总有解,则实数的范围为___________.
◎导数的综合应用
1.(2021·全国·高三阶段练习(文))已知,.
(Ⅰ)讨论的单调性;
(Ⅱ)若,证明:.
2.(2022·福建永泰·高二期末)已知函数.
(1)当时,求函数的极值;
(2)若对,恒成立,求的取值范围.
3.(2022·江西南昌·高二期末(理))已知函数.
(1)若,求函数的单调区间;
(2)设存在两个极值点,且,若,求证:.
巩固提升
一、单选题
1.已知定义在上的函数的部分图象如图所示,则下列说法正确的是( )
A.有极小值 B.有最大值
C.是奇函数 D.是偶函数
2.函数有( )
A.极大值点3 B.极小值点3
C.极大值点1 D.极小值点1
3.函数在处有极值为,则的值为( )
A. B.
C. D.
4.已知函数既有极大值,又有极小值,则实数a的取值范围是( )
A. B.
C. D.
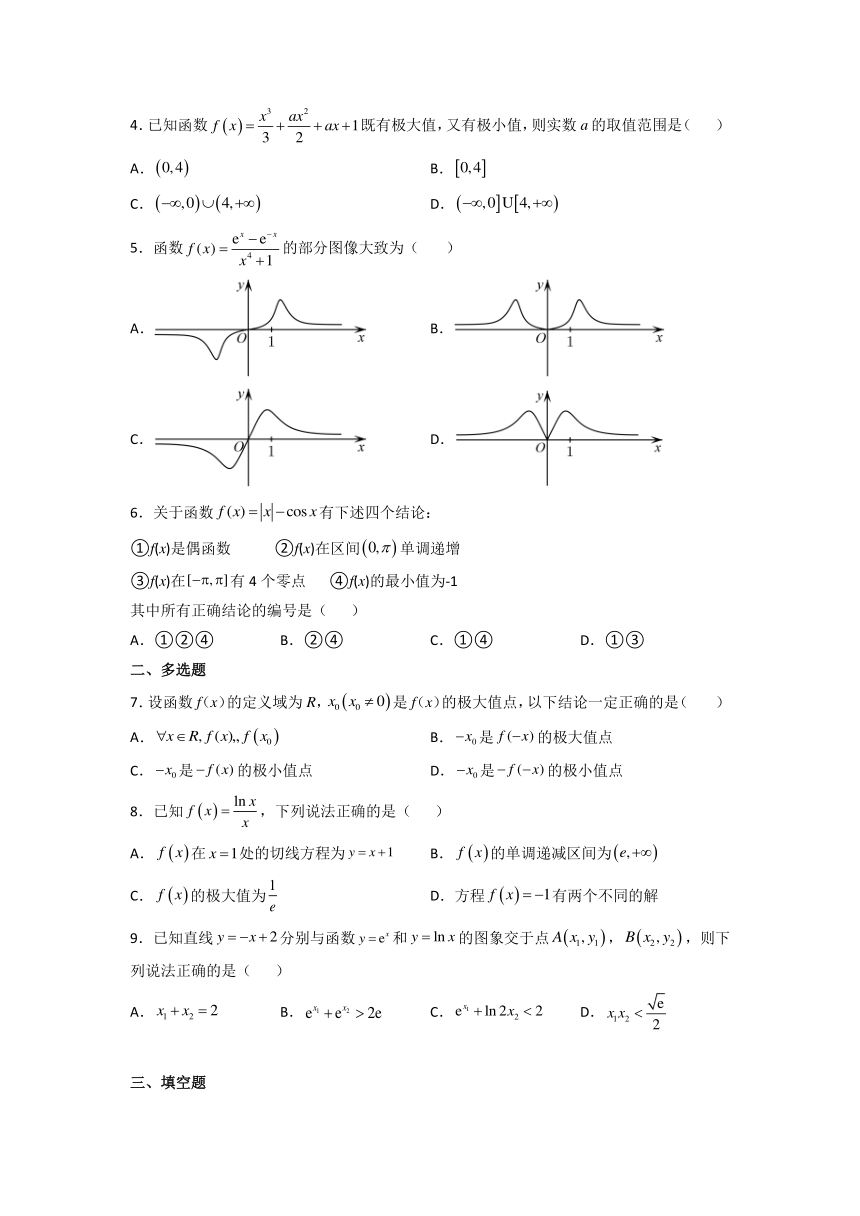
5.函数的部分图像大致为( )
A. B.
C. D.
6.关于函数有下述四个结论:
①f(x)是偶函数 ②f(x)在区间单调递增
③f(x)在有4个零点 ④f(x)的最小值为-1
其中所有正确结论的编号是( )
A.①②④ B.②④ C.①④ D.①③
二、多选题
7.设函数f(x)的定义域为R,是f(x)的极大值点,以下结论一定正确的是( )
A. B.是的极大值点
C.是的极小值点 D.是的极小值点
8.已知,下列说法正确的是( )
A.在处的切线方程为 B.的单调递减区间为
C.的极大值为 D.方程有两个不同的解
9.已知直线分别与函数和的图象交于点,,则下列说法正确的是( )
A. B. C. D.
三、填空题
10.函数y=在[0,2]上的最大值为________.
11.已知(a>0,b>0)在x=1处取得极值,则的最小值为___________.
12.函数仅有一个零点,则实数的取值范围是_________.
四、解答题
13.设函数.
(1)求的值;
(2)求的极大值.
14.已知函数.
(1)求函数在区间上的最大值和最小值;
(2)求出方程的解的个数.
15.已知函数在与处都取得极值.
(1)求a,b的值;
(2)若对任意,不等式恒成立,求实数c的取值范围.
16.已知函数
(1)讨论的单调性;
(2)当时,证明
参考答案:
1.A
由导函数f′(x)的图象知
在x=-2处f′(-2)=0,且其两侧导数符号为左正右负,x=-2是极大值;
在x=-1处f′(-1)=0,且其两侧导数符号为左负右正,x=-1是极小值;
在x=-3处f′(2)=0,且其两侧导数符号为左正右负,x=2是极大值;
所以f(x)的极小值点的个数为1,
故选:A
2.D
A:因为函数是实数集上的增函数,所以函数没有极值;
B:因为函数是正实数集上的增函数,所以函数没有极值;
C:因为函数在区间、上是减函数,所以函数没有极值;
D:因为,所以该函数在上是增函数,在上是减函数,因此是函数的极小值点,符合题意,
故选:D
3.C
时,不一定是极值点,还需要在两侧的单调性不相同.
是的极值点时,由于在上连续,所以.
所以是为函数极值点的必要不充分条件.
故选:C
4.BC
由的导函数的图象可知,函数在、上单调递减,在、上单调递增,
故当或时,取得极小值;当时,取得极大值,故BC正确,AD错误.
故选:BC.
◎求函数的极值
1.2
由题意可得.由,得或;由,得,则在和上单调递增,在上单调递减,则.
故答案为:
2.(1);(2)单调增区间,,单调减区间;极小值为,极大值为.
解:(1),所以,
故切线方程为;
(2),
解,得或;解,得;
所以,为函数的单调增区间,
为函数的单调减区间
所以的极小值为,极大值为.
◎求函数的最值
1.(1),;(2)最小值是-2,最大值是2.
解:(1),
∵函数在处取得极值2,
∴,解得,
,经验证在处取极值2,故,
(2)由,令,解得
令,解得或,
因此,在递减,在递增,的最小值是
而,故函数的最大值是2.
◎含参数问题
1.C
解:由,得,
因为在处有极值0,
所以,即,解得或,
当时,,则 在上单调递增,此时函数无极值,所以舍去,
当时,,令,得或,经检验 和都为函数的极值点,
综上,
所以,
故选:C
2.(1);(2)存在,a=2,b=3或a=-2,b=-29.
(1)由于,所以.
依题意,可得且.
即解得
(2)存在,,
令,解得x1=0,x2=4(舍去).
①当a>0,x变化时,f'(x),f(x)的变化情况如下表
x (-1,0) 0 (0,2)
+ 0 -
f(x) ↗ 极大值 ↘
所以当x=0时,f(x)取得最大值.所以b=3.
又f(2)=-16a+3,f(-1)=-7a+3,f(-1)>f(2),所以当x=2时,f(x)取得最小值,
所以-16a+3=-29,即a=2.
②当a<0,x变化时,f'(x),f(x)的变化情况如下表:
x (-1,0) 0 (0,2)
- 0 +
f(x) ↘ 极小值 ↗
所以当x=0时,f(x)取得最小值.所以b=-29.
又f(2)=-16a-29,f(-1)=-7a-29,f(2)>f(-1),所以当x=2时,f(x)取得最大值,
所以-16a-29=3,即a=-2.
综上所述,a=2,b=3或a=-2,b=-29.
3.
函数定义域为R,.
令,则.
当时,有,,即恒成立,所以在R上单增,无极值;
当时,有,有两个根(不妨设),令解得:;令解得:,所以在上单增,在上单减,所以在处取得极大值,在处取得极小值.
故实数a的取值范围是.
故答案为:
4.
由有解,记,,.
为增,,,为减,.,
由有解,则,.
故答案为:
◎导数的综合应用
1.(Ⅰ)答案见解析;(Ⅱ)证明见解析.
(Ⅰ)由题可知,.
当时,恒成立,函数在上单调递增;
当时,令,解得.
当时,,在上单调递增;
当时,,函数在上单调递减.
综上可知,当时,函数在上单调递增;当时,函数在上单调递增,在上单调递减.
(Ⅱ)证明:若,则由(Ⅰ)可知,在处取得极大值,
.
令.,,
函数在上单调递减.
又,,
.
【点睛】
关键点点睛:第(Ⅱ)问的关键点是:通过构造函数证得.
2.(1)极小值为,无极大值;(2).
(1)函数的定义域为,
当时,.由,得.
当变化时,,的变化情况如下表
- 0 +
单调递减 极小值 单调递增
所以在上单调递减,上单调递增,
所以函数的极小值为,无极大值.
(2)对,恒成立,即对,恒成立.
令,则.由得,
当时,,单调递增;
当时,,单调递减,
所以,因此.
所以的取值范围是.
3.(1)在和上单调递增,在上单调递减;
(2)证明见解析
(1)
解:当时,,所以,令,解得或,令,解得,所以函数在和上单调递增,在上单调递减;
(2)
解:,
,,
因为存在两个极值点,,所以存在两个互异的正实数根,,
所以,,则,所以,
所以
,
令,
则,
,,
在上单调递减,
,而,
即,
.
巩固提升
1.A
由图可知:有极小值,无最大值,且的定义域为,,
所以该函数不是奇函数,同时函数图象不关于轴对称,故不为偶函数,
所以答案为A
故选:A
2.A
∵,
∴,
当时,单调递增;当时,单调递减.
∴在处取得极大值,即只有一个极值点,且是极大值点,
故选:.
3.B
因为函数,
所以,
所以,,
解得a=2,b=5,
=-3,
故选:B
4.C
由题意知,,
由函数有极小值和极大值,
得方程有两个不同的实根,
所以或,
即的取值范围为.
故选:C
5.C
解:因为函数的定义域为R,且,所以函数是奇函数,排除B、D选项,
又,所以,
令,则,
令,解得,而,
所以当时,,所以单调递减,且,
,
所以存在,使得,即存在,使得,且 时,,函数单调递增, 时,,函数单调递减,
所以排除A选项,
故选:C.
6.A
选项①,由,所以是偶函数,故正确.
选项②,当时,,则
所以在上单调递增, 故正确.
选项③,由②可知,在上单调递增,且,
所以函数在上有唯一零点,
又根据①是偶函数,则函数在上有唯一零点
所以在有两个零点,故不正确.
选项④,由前面可知函数在单调递减,在上单调递增
所以,故正确.
故选:A
7.BD
对A. 是的极大值点,并不是最大值点,故A不正确;
对B. 相当于关于轴的对称图象,故应是的极大值点,故B正确;
对C. 相当于关于轴的对称图象,故应是的极小值点,跟没有关系,故C不正确;
对D. 相当于先关于轴的对称,再关于轴的对称图象.故D正确.
故选:BD.
8.BC
对于A,由(),得,,则,所以在处的切线方程为,所以A错误,
对于B,由,得,,所以的单调递减区间为,所以B正确,
对于C,由,得,当时,,当时,,所以当时,取得极大值,所以C正确,
对于D,由C选项可知的最大值为,且当时,,当时,, 所以函数与的交点个数为1,所以有1个解,所以D错误,
故选:BC
9.ABD
函数与互为反函数,则与的图象关于对称,
将与联立,则,
由直线分别与函数和的图象交于点,
作出函数图象:
则的中点坐标为,
对于A,由,解得,故A正确;
对于B,,
因为,即等号不成立,所以,故B正确;
对于D,记,则,,则,又,令,则,
当时,在上单调递增,
故,故D正确.
对于C,令,
,令,,
当时,,所以单调递减,所以,
所以, 所以在上单调递减,所以,
故C错误;
故选:ABD.
10.
∵y′==,
令y′=0,得x=1∈[0,2].
∴f(1)=,f(0)=0,f(2)=.
∴f(x)max=f(1)=.
故答案为:
11.
解:因为,所以,因为函数在处取得极值,所以,即,因为,,
所以当且仅当,即,时取等号;
故答案为:
12.
【解析】
解:由题意可得:函数,
所以,
令,则或,
令,则,
所以函数的单调增区间为和,减区间为
所以当时函数有极大值,
当时函数有极小值,,
因为函数仅有一个零点,,
所以或,
解得或.
所以实数的取值范围是
故答案为:
13.(1)-3
(2)2
(1)
解:因为函数,
所以,
所以;
(2)
令,得,
当或时,,
当时,,
所以当时,取得极大值.
14.(1)f(x)的最大值为7,最小值为-33;
(2)见解析.
(1)
0 2 3
+ - +
f(-2)=-33 ↗ f(0)=7 ↘ f(2)=-1 ↗ f(3)=7
∴f(x)的最大值为7,最小值为-33;
(2)
0 2
+ - +
↗ f(0)=7 ↘ f(2)=-1 ↗
当a<-1或a>7时,方程有一个根;
当a=-1或7时,方程有两个根;
当-1<a<7时,方程有三个根.
15.(1),;
(2).
(1)
由题设,,
又,,
解得,.
(2)
由(1)得,即,
当时,,随的变化情况如下表:
1
+ 0 - 0 +
递增 极大值 递减 极小值 递增
∴在上单调递增,在上单调递减,在上单调递增,
∴当时,为极大值,
又,显然f(-)<f(2),
所以为在上的最大值.
要使对任意恒成立,则只需,
解得或c>1.
∴实数c的取值范围为.
16.(1)答案见解析
(2)证明见解析
(1)
解:函数的定义域为,
,
∴当时,在上恒成立,故函数在区间上单调递增;
当时,由得,由得,即函数在区间上单调递增,在上单调递减;
综上,当时,在区间上单调递增;当时,在区间上单调递增,在上单调递减;
(2)
证明:因为时,证明,只需证明,
由(1)知,当时,函数在区间上单调递增,在上单调递减;
所以.
令,则,
所以当时,,函数单调递减;
当时,,函数单调递增,
所以.
所以时, ,
所以当时,
◎判断函数的极值点与极值
1.(2021·全国·高二课时练习) 如图是f(x)的导函数f′(x)的图象,则f(x)的极小值点的个数为( )
A.1 B.2 C.3 D.4
2.(2021·广西·昭平中学高二阶段练习(理))下列函数中,存在极值的函数为( )
A. B. C. D.
3.(2021·山东·广饶一中练习)已知在上连续,是的导函数,则是为函数极值点的( )条件.
A.充要条件 B.充分不必要 C.必要不充分 D.既不充分也不必要
4.(2022·重庆八中高二期末)(多选)函数的导函数的图象如图所示,则下列说法正确的有( )
A.为函数的一个零点
B.为函数的一个极大值点
C.函数在区间上单调递增
D.是函数的最大值
◎求函数的极值
1.(2022·河南驻马店·期末(文))函数的极小值是______.
2.(2021·广西·钦州一中高二期中(文))已知函数.
(1)求曲线在点处的切线方程;
(2)求函数的单调区间和极值.
◎求函数的最值
1.(2021·全国·专题练习(理))已知函数在处有极值2.
(1)求,的值;
(2)求函数在区间上的最值.
◎含参数问题
1.(2021·江苏·南京市宁海中学高二期中)已知函数在处有极值0,则的值为( )
A.4 B.7 C.11 D.4或11
2.(2021·江苏·高二专题练习)(1)若函数f(x)=ax3+bx-4在x=1处取得极值,且极值为0,求实数a,b的值;
(2)已知函数f(x)=ax3-6ax2+b(a≠0),是否存在实数a,b使f(x)在区间[-1,2]上取得最大值3,最小值-29 若存在,求出a,b的值;若不存在,请说明理由.
3.(2022·全国·高二课时练习)若函数既有极大值又有极小值,则实数a的取值范围是______.
4.(2021·湖北·应城市第一高级中学高三阶段练习)已知方程对总有解,则实数的范围为___________.
◎导数的综合应用
1.(2021·全国·高三阶段练习(文))已知,.
(Ⅰ)讨论的单调性;
(Ⅱ)若,证明:.
2.(2022·福建永泰·高二期末)已知函数.
(1)当时,求函数的极值;
(2)若对,恒成立,求的取值范围.
3.(2022·江西南昌·高二期末(理))已知函数.
(1)若,求函数的单调区间;
(2)设存在两个极值点,且,若,求证:.
巩固提升
一、单选题
1.已知定义在上的函数的部分图象如图所示,则下列说法正确的是( )
A.有极小值 B.有最大值
C.是奇函数 D.是偶函数
2.函数有( )
A.极大值点3 B.极小值点3
C.极大值点1 D.极小值点1
3.函数在处有极值为,则的值为( )
A. B.
C. D.
4.已知函数既有极大值,又有极小值,则实数a的取值范围是( )
A. B.
C. D.
5.函数的部分图像大致为( )
A. B.
C. D.
6.关于函数有下述四个结论:
①f(x)是偶函数 ②f(x)在区间单调递增
③f(x)在有4个零点 ④f(x)的最小值为-1
其中所有正确结论的编号是( )
A.①②④ B.②④ C.①④ D.①③
二、多选题
7.设函数f(x)的定义域为R,是f(x)的极大值点,以下结论一定正确的是( )
A. B.是的极大值点
C.是的极小值点 D.是的极小值点
8.已知,下列说法正确的是( )
A.在处的切线方程为 B.的单调递减区间为
C.的极大值为 D.方程有两个不同的解
9.已知直线分别与函数和的图象交于点,,则下列说法正确的是( )
A. B. C. D.
三、填空题
10.函数y=在[0,2]上的最大值为________.
11.已知(a>0,b>0)在x=1处取得极值,则的最小值为___________.
12.函数仅有一个零点,则实数的取值范围是_________.
四、解答题
13.设函数.
(1)求的值;
(2)求的极大值.
14.已知函数.
(1)求函数在区间上的最大值和最小值;
(2)求出方程的解的个数.
15.已知函数在与处都取得极值.
(1)求a,b的值;
(2)若对任意,不等式恒成立,求实数c的取值范围.
16.已知函数
(1)讨论的单调性;
(2)当时,证明
参考答案:
1.A
由导函数f′(x)的图象知
在x=-2处f′(-2)=0,且其两侧导数符号为左正右负,x=-2是极大值;
在x=-1处f′(-1)=0,且其两侧导数符号为左负右正,x=-1是极小值;
在x=-3处f′(2)=0,且其两侧导数符号为左正右负,x=2是极大值;
所以f(x)的极小值点的个数为1,
故选:A
2.D
A:因为函数是实数集上的增函数,所以函数没有极值;
B:因为函数是正实数集上的增函数,所以函数没有极值;
C:因为函数在区间、上是减函数,所以函数没有极值;
D:因为,所以该函数在上是增函数,在上是减函数,因此是函数的极小值点,符合题意,
故选:D
3.C
时,不一定是极值点,还需要在两侧的单调性不相同.
是的极值点时,由于在上连续,所以.
所以是为函数极值点的必要不充分条件.
故选:C
4.BC
由的导函数的图象可知,函数在、上单调递减,在、上单调递增,
故当或时,取得极小值;当时,取得极大值,故BC正确,AD错误.
故选:BC.
◎求函数的极值
1.2
由题意可得.由,得或;由,得,则在和上单调递增,在上单调递减,则.
故答案为:
2.(1);(2)单调增区间,,单调减区间;极小值为,极大值为.
解:(1),所以,
故切线方程为;
(2),
解,得或;解,得;
所以,为函数的单调增区间,
为函数的单调减区间
所以的极小值为,极大值为.
◎求函数的最值
1.(1),;(2)最小值是-2,最大值是2.
解:(1),
∵函数在处取得极值2,
∴,解得,
,经验证在处取极值2,故,
(2)由,令,解得
令,解得或,
因此,在递减,在递增,的最小值是
而,故函数的最大值是2.
◎含参数问题
1.C
解:由,得,
因为在处有极值0,
所以,即,解得或,
当时,,则 在上单调递增,此时函数无极值,所以舍去,
当时,,令,得或,经检验 和都为函数的极值点,
综上,
所以,
故选:C
2.(1);(2)存在,a=2,b=3或a=-2,b=-29.
(1)由于,所以.
依题意,可得且.
即解得
(2)存在,,
令,解得x1=0,x2=4(舍去).
①当a>0,x变化时,f'(x),f(x)的变化情况如下表
x (-1,0) 0 (0,2)
+ 0 -
f(x) ↗ 极大值 ↘
所以当x=0时,f(x)取得最大值.所以b=3.
又f(2)=-16a+3,f(-1)=-7a+3,f(-1)>f(2),所以当x=2时,f(x)取得最小值,
所以-16a+3=-29,即a=2.
②当a<0,x变化时,f'(x),f(x)的变化情况如下表:
x (-1,0) 0 (0,2)
- 0 +
f(x) ↘ 极小值 ↗
所以当x=0时,f(x)取得最小值.所以b=-29.
又f(2)=-16a-29,f(-1)=-7a-29,f(2)>f(-1),所以当x=2时,f(x)取得最大值,
所以-16a-29=3,即a=-2.
综上所述,a=2,b=3或a=-2,b=-29.
3.
函数定义域为R,.
令,则.
当时,有,,即恒成立,所以在R上单增,无极值;
当时,有,有两个根(不妨设),令解得:;令解得:,所以在上单增,在上单减,所以在处取得极大值,在处取得极小值.
故实数a的取值范围是.
故答案为:
4.
由有解,记,,.
为增,,,为减,.,
由有解,则,.
故答案为:
◎导数的综合应用
1.(Ⅰ)答案见解析;(Ⅱ)证明见解析.
(Ⅰ)由题可知,.
当时,恒成立,函数在上单调递增;
当时,令,解得.
当时,,在上单调递增;
当时,,函数在上单调递减.
综上可知,当时,函数在上单调递增;当时,函数在上单调递增,在上单调递减.
(Ⅱ)证明:若,则由(Ⅰ)可知,在处取得极大值,
.
令.,,
函数在上单调递减.
又,,
.
【点睛】
关键点点睛:第(Ⅱ)问的关键点是:通过构造函数证得.
2.(1)极小值为,无极大值;(2).
(1)函数的定义域为,
当时,.由,得.
当变化时,,的变化情况如下表
- 0 +
单调递减 极小值 单调递增
所以在上单调递减,上单调递增,
所以函数的极小值为,无极大值.
(2)对,恒成立,即对,恒成立.
令,则.由得,
当时,,单调递增;
当时,,单调递减,
所以,因此.
所以的取值范围是.
3.(1)在和上单调递增,在上单调递减;
(2)证明见解析
(1)
解:当时,,所以,令,解得或,令,解得,所以函数在和上单调递增,在上单调递减;
(2)
解:,
,,
因为存在两个极值点,,所以存在两个互异的正实数根,,
所以,,则,所以,
所以
,
令,
则,
,,
在上单调递减,
,而,
即,
.
巩固提升
1.A
由图可知:有极小值,无最大值,且的定义域为,,
所以该函数不是奇函数,同时函数图象不关于轴对称,故不为偶函数,
所以答案为A
故选:A
2.A
∵,
∴,
当时,单调递增;当时,单调递减.
∴在处取得极大值,即只有一个极值点,且是极大值点,
故选:.
3.B
因为函数,
所以,
所以,,
解得a=2,b=5,
=-3,
故选:B
4.C
由题意知,,
由函数有极小值和极大值,
得方程有两个不同的实根,
所以或,
即的取值范围为.
故选:C
5.C
解:因为函数的定义域为R,且,所以函数是奇函数,排除B、D选项,
又,所以,
令,则,
令,解得,而,
所以当时,,所以单调递减,且,
,
所以存在,使得,即存在,使得,且 时,,函数单调递增, 时,,函数单调递减,
所以排除A选项,
故选:C.
6.A
选项①,由,所以是偶函数,故正确.
选项②,当时,,则
所以在上单调递增, 故正确.
选项③,由②可知,在上单调递增,且,
所以函数在上有唯一零点,
又根据①是偶函数,则函数在上有唯一零点
所以在有两个零点,故不正确.
选项④,由前面可知函数在单调递减,在上单调递增
所以,故正确.
故选:A
7.BD
对A. 是的极大值点,并不是最大值点,故A不正确;
对B. 相当于关于轴的对称图象,故应是的极大值点,故B正确;
对C. 相当于关于轴的对称图象,故应是的极小值点,跟没有关系,故C不正确;
对D. 相当于先关于轴的对称,再关于轴的对称图象.故D正确.
故选:BD.
8.BC
对于A,由(),得,,则,所以在处的切线方程为,所以A错误,
对于B,由,得,,所以的单调递减区间为,所以B正确,
对于C,由,得,当时,,当时,,所以当时,取得极大值,所以C正确,
对于D,由C选项可知的最大值为,且当时,,当时,, 所以函数与的交点个数为1,所以有1个解,所以D错误,
故选:BC
9.ABD
函数与互为反函数,则与的图象关于对称,
将与联立,则,
由直线分别与函数和的图象交于点,
作出函数图象:
则的中点坐标为,
对于A,由,解得,故A正确;
对于B,,
因为,即等号不成立,所以,故B正确;
对于D,记,则,,则,又,令,则,
当时,在上单调递增,
故,故D正确.
对于C,令,
,令,,
当时,,所以单调递减,所以,
所以, 所以在上单调递减,所以,
故C错误;
故选:ABD.
10.
∵y′==,
令y′=0,得x=1∈[0,2].
∴f(1)=,f(0)=0,f(2)=.
∴f(x)max=f(1)=.
故答案为:
11.
解:因为,所以,因为函数在处取得极值,所以,即,因为,,
所以当且仅当,即,时取等号;
故答案为:
12.
【解析】
解:由题意可得:函数,
所以,
令,则或,
令,则,
所以函数的单调增区间为和,减区间为
所以当时函数有极大值,
当时函数有极小值,,
因为函数仅有一个零点,,
所以或,
解得或.
所以实数的取值范围是
故答案为:
13.(1)-3
(2)2
(1)
解:因为函数,
所以,
所以;
(2)
令,得,
当或时,,
当时,,
所以当时,取得极大值.
14.(1)f(x)的最大值为7,最小值为-33;
(2)见解析.
(1)
0 2 3
+ - +
f(-2)=-33 ↗ f(0)=7 ↘ f(2)=-1 ↗ f(3)=7
∴f(x)的最大值为7,最小值为-33;
(2)
0 2
+ - +
↗ f(0)=7 ↘ f(2)=-1 ↗
当a<-1或a>7时,方程有一个根;
当a=-1或7时,方程有两个根;
当-1<a<7时,方程有三个根.
15.(1),;
(2).
(1)
由题设,,
又,,
解得,.
(2)
由(1)得,即,
当时,,随的变化情况如下表:
1
+ 0 - 0 +
递增 极大值 递减 极小值 递增
∴在上单调递增,在上单调递减,在上单调递增,
∴当时,为极大值,
又,显然f(-)<f(2),
所以为在上的最大值.
要使对任意恒成立,则只需,
解得或c>1.
∴实数c的取值范围为.
16.(1)答案见解析
(2)证明见解析
(1)
解:函数的定义域为,
,
∴当时,在上恒成立,故函数在区间上单调递增;
当时,由得,由得,即函数在区间上单调递增,在上单调递减;
综上,当时,在区间上单调递增;当时,在区间上单调递增,在上单调递减;
(2)
证明:因为时,证明,只需证明,
由(1)知,当时,函数在区间上单调递增,在上单调递减;
所以.
令,则,
所以当时,,函数单调递减;
当时,,函数单调递增,
所以.
所以时, ,
所以当时,
