沪科版数学八上16.4角的平分线
图片预览










文档简介
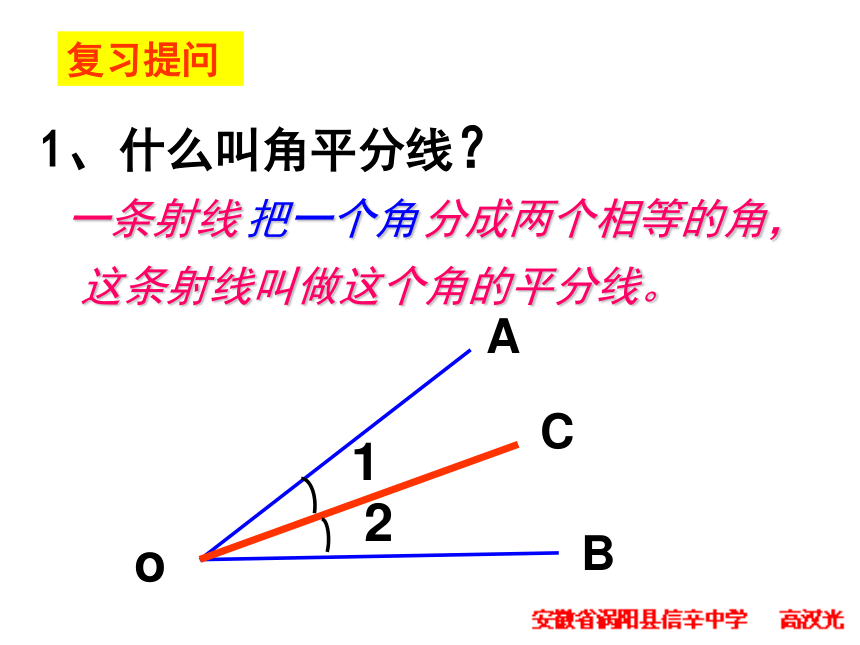
课件31张PPT。oBCA16.4角的平分线复习提问1、什么叫角平分线?一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。oBCA复习提问 2、点到直线距离:从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
在半透明的纸上画∠BAC,对折,使角的两条边完全重合,然后用直尺画出折痕OD.
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线.BCAD情景引入 不利用作图工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?探究: 如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?用尺规作图的方法作出角的平分线已知:如图,∠AOB。
求作:∠AOB的平分线。画法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N. 2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.3.作射线OC.射线OC即为所求.BA.CE D过直线上一点作这条直线的垂线画法: 1.以C为圆心,适当长为半径作弧,交AB于D,E. 2.分别以D,E为圆心.大于 1/2 DE的长为半径作弧.两弧交于F.3.作直线FC.直线FC.即为所求.
FAD过直线外一点作这条直线的垂线BE.kc画法: 1.任意取一点K,使K和 C在AB两 旁. 3.分别以D,E为圆心.大于 1/2 DE的长为半径作弧.两弧交于F.4.作直线FC。即为所求.
2.以C为圆心,CK长为半径作弧,交AB于D,E.F角平分线的性质 已知:如下图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D,E。
求证:PD=PE。定理:角的平分线上的点到角的两边的距离相等∴PD=PE(全等三角形的对应边相等)。证明:∴OC是∠AOB的平分线(已知),∴∠1=∠2(角平分线的定义)。 ∵PD⊥OA,PE⊥OB(已知),∴∠PDO=∠PEO=90°(垂直的定义)。在△PDO和△PEO中,∠PDO=∠PEO (已证),∠1=∠2(已证),OP=OP(公共边),∴△PDO≌△PEO (AAS)。已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
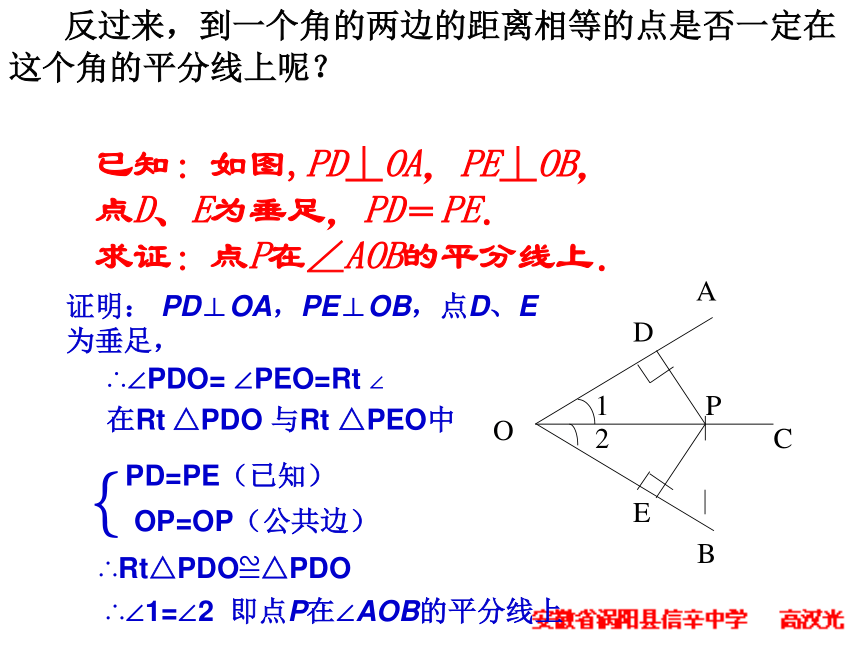
求证:点P在∠AOB的平分线上.证明: PD⊥OA,PE⊥OB,点D、E为垂足,在Rt △PDO 与Rt △PEO中∴∠PDO= ∠PEO=Rt ∠PD=PE(已知){OP=OP(公共边)∴Rt△PDO≌△PDO∴∠1=∠2 即点P在∠AOB的平分线上 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?
角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上.
角平分线的性质定理和角平分线的判定定理
是证明角相等、线段相等的新途径.
例1: 已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P在∠BAC的角平分线上ABCMNP 证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PF.
∴AP平分∠BAC
已知:如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F。
求证:点F在∠DAE的平分线上。变式 例2. 已知:如图,△ABC的外角∠CBD和∠BCE的平分线相交于点P。
求证:(1)点P到三边AB,BC,CA所在直线的距离相等;
(2)点P在∠DAE的平分线上。又∵ 点P在∠CBD的角平分线
∴ PM=PK(在角的平分线上的点
到这个角的两边的距离相等)
同理 PN=PK
∴ PM=PK=PN
即,点P到三边AB,BC,CA所在直线的距离相等证明:(1)过点P分别作AB,AE,BC所在直线的垂线,垂足分别是点M,N,K.例3. 要在S区建一个集贸市场,使它到公路和铁路距离相等,且离公路和铁路的交叉处500米,该集贸市场应建在何处?(比例尺 1:20 000)解:设要截取的长度为Xm,则: 解得:X=0.025
0.025 m =2.5cm则点A即为所求的点A 例4.如图,已知△ABC的外角∠DAB和 ∠ABE的平分线相交于点F,
求证:点F在∠DCE的平分线上. 证明:过点F作FG⊥AD于G,FH⊥BE于H,FM⊥AB于M, ∵点F在∠DAB的平分线上, FG⊥AD,FM⊥AB,∴FG=FM. 又∵点F在∠ABE的平分线上,FH⊥BE, FM⊥AB,∴FM=FH,∴FG=FH, ∴点F在∠DAE的平分线上. ∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)判断:练习∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等1.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。 求证:AD是△ABC的角平分线。巩固提高 2.在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,DE⊥AB,BC=7,DE=3.求BD的长。 3.如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB 内心:三角形的三内角平分线交于一点,这点叫做三角形的内心.
三角形的内心到三角形三边的距离相等.三角形的五心: 旁心:三角形的一内角平分线和另外两顶点处的外角平分线交于一点,这点叫做三角形的旁心.
三角形有三个旁心.
三角形的内心到三角形三边的距离相等. 重心:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍,上述交点叫做三角形的重心. 垂心:三角形的三条高交于一点,这点叫做三角形的垂心.ABCP 外心:三角形的三条垂直平分线交于一点,这点叫做三角形的外心.小结:1:画一个已知角的角平分线;2:角平分线的性质:角的平分线上的点到角的两边的距离相等.
3:角平分线的判定结论:到角的两边的距离相等的点在角平分线上。
在半透明的纸上画∠BAC,对折,使角的两条边完全重合,然后用直尺画出折痕OD.
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线.BCAD情景引入 不利用作图工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?探究: 如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?用尺规作图的方法作出角的平分线已知:如图,∠AOB。
求作:∠AOB的平分线。画法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N. 2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.3.作射线OC.射线OC即为所求.BA.CE D过直线上一点作这条直线的垂线画法: 1.以C为圆心,适当长为半径作弧,交AB于D,E. 2.分别以D,E为圆心.大于 1/2 DE的长为半径作弧.两弧交于F.3.作直线FC.直线FC.即为所求.
FAD过直线外一点作这条直线的垂线BE.kc画法: 1.任意取一点K,使K和 C在AB两 旁. 3.分别以D,E为圆心.大于 1/2 DE的长为半径作弧.两弧交于F.4.作直线FC。即为所求.
2.以C为圆心,CK长为半径作弧,交AB于D,E.F角平分线的性质 已知:如下图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D,E。
求证:PD=PE。定理:角的平分线上的点到角的两边的距离相等∴PD=PE(全等三角形的对应边相等)。证明:∴OC是∠AOB的平分线(已知),∴∠1=∠2(角平分线的定义)。 ∵PD⊥OA,PE⊥OB(已知),∴∠PDO=∠PEO=90°(垂直的定义)。在△PDO和△PEO中,∠PDO=∠PEO (已证),∠1=∠2(已证),OP=OP(公共边),∴△PDO≌△PEO (AAS)。已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上.证明: PD⊥OA,PE⊥OB,点D、E为垂足,在Rt △PDO 与Rt △PEO中∴∠PDO= ∠PEO=Rt ∠PD=PE(已知){OP=OP(公共边)∴Rt△PDO≌△PDO∴∠1=∠2 即点P在∠AOB的平分线上 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?
角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上.
角平分线的性质定理和角平分线的判定定理
是证明角相等、线段相等的新途径.
例1: 已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P在∠BAC的角平分线上ABCMNP 证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PF.
∴AP平分∠BAC
已知:如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F。
求证:点F在∠DAE的平分线上。变式 例2. 已知:如图,△ABC的外角∠CBD和∠BCE的平分线相交于点P。
求证:(1)点P到三边AB,BC,CA所在直线的距离相等;
(2)点P在∠DAE的平分线上。又∵ 点P在∠CBD的角平分线
∴ PM=PK(在角的平分线上的点
到这个角的两边的距离相等)
同理 PN=PK
∴ PM=PK=PN
即,点P到三边AB,BC,CA所在直线的距离相等证明:(1)过点P分别作AB,AE,BC所在直线的垂线,垂足分别是点M,N,K.例3. 要在S区建一个集贸市场,使它到公路和铁路距离相等,且离公路和铁路的交叉处500米,该集贸市场应建在何处?(比例尺 1:20 000)解:设要截取的长度为Xm,则: 解得:X=0.025
0.025 m =2.5cm则点A即为所求的点A 例4.如图,已知△ABC的外角∠DAB和 ∠ABE的平分线相交于点F,
求证:点F在∠DCE的平分线上. 证明:过点F作FG⊥AD于G,FH⊥BE于H,FM⊥AB于M, ∵点F在∠DAB的平分线上, FG⊥AD,FM⊥AB,∴FG=FM. 又∵点F在∠ABE的平分线上,FH⊥BE, FM⊥AB,∴FM=FH,∴FG=FH, ∴点F在∠DAE的平分线上. ∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)判断:练习∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等1.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。 求证:AD是△ABC的角平分线。巩固提高 2.在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,DE⊥AB,BC=7,DE=3.求BD的长。 3.如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB 内心:三角形的三内角平分线交于一点,这点叫做三角形的内心.
三角形的内心到三角形三边的距离相等.三角形的五心: 旁心:三角形的一内角平分线和另外两顶点处的外角平分线交于一点,这点叫做三角形的旁心.
三角形有三个旁心.
三角形的内心到三角形三边的距离相等. 重心:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍,上述交点叫做三角形的重心. 垂心:三角形的三条高交于一点,这点叫做三角形的垂心.ABCP 外心:三角形的三条垂直平分线交于一点,这点叫做三角形的外心.小结:1:画一个已知角的角平分线;2:角平分线的性质:角的平分线上的点到角的两边的距离相等.
3:角平分线的判定结论:到角的两边的距离相等的点在角平分线上。
