2021-2022九年级下学期 第三章《圆》单元检测(提升卷1)(含解析)
文档属性
| 名称 | 2021-2022九年级下学期 第三章《圆》单元检测(提升卷1)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 10:23:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章《圆》检测卷
(提升卷1)
第I卷(选择题)
一、选择题(本大题共10小题,每小题3分,共30分)
1.如图,点A、B、C是⊙O上的三个点,若∠AOB=82°,则∠C的度数为( )
A.82° B.38° C.24° D.41°
2. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是
A.相交 B.相切 C.相离 D.无法确定
3.如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且弧CE=弧CD,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,OB=4,则AB的长为( )
A.2 B.4 C.6 D.4
5.一个扇形的圆心角是120°,半径为3,则这个扇形的面积为( )
A. B. C. D.
6.如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
A.40° B.50° C.80° D.100°
7.如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
A.50° B.60° C.70° D.80°
8.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
9.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC= ,则图中阴影部分的面积是( )
A. B. C. D.
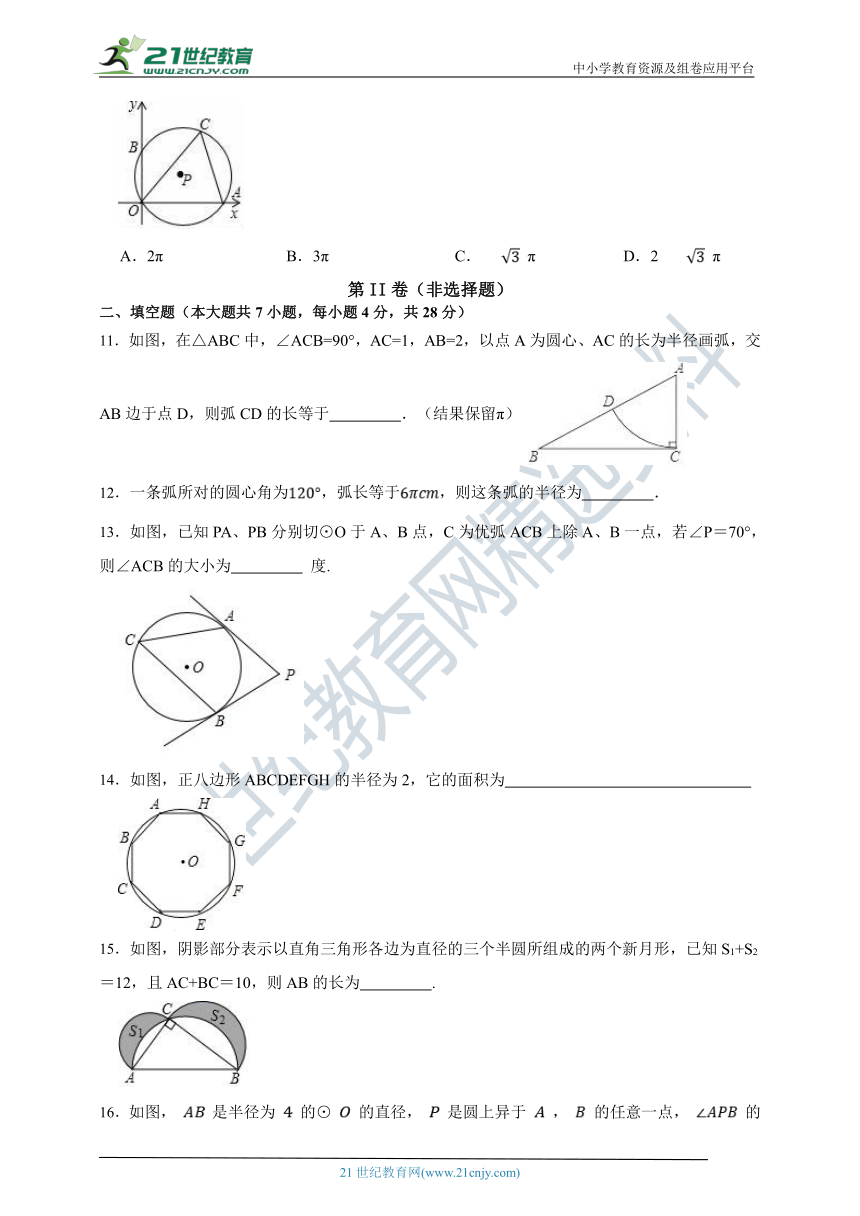
10.如图,已知⊙P与坐标轴交于点A,O,B,点C在⊙P上,且∠ACO=60°,若点B的坐标为(0,3),则弧OA的长为( )
A.2π B.3π C. π D.2 π
第II卷(非选择题)
二、填空题(本大题共7小题,每小题4分,共28分)
11.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)
12.一条弧所对的圆心角为,弧长等于,则这条弧的半径为 .
13.如图,已知PA、PB分别切⊙O于A、B点,C为优弧ACB上除A、B一点,若∠P=70°,则∠ACB的大小为 度.
14.如图,正八边形ABCDEFGH的半径为2,它的面积为
15.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=12,且AC+BC=10,则AB的长为 .
16.如图, 是半径为 的⊙ 的直径, 是圆上异于 , 的任意一点, 的平分线交⊙ 于点 ,连接 和 ,△ 的中位线所在的直线与⊙ 相交于点 、 ,则 的长是
17.如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在 上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是 .
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,过点D作DE∥BC,交⊙O于点E,连接CE.
求证:四边形DBCE是平行四边形.
19.如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
20.已知AB为 的直径,EF切 于点D,过点B作 于点H交 于点C,连接BD.
(1)如图①,若 ,求 的大小;
(2)如图②,若C为弧BD的中点,求 的大小.
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.
(1)求证:DE是⊙O的切线;
(2)当DE=1,∠C=30°时,求图中阴影部分的面积.
22.如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.
23.如图,⊙O中,AB、CD是⊙O的直径,F是⊙O上一点,连接BC、BF,若点B是弧CF的中点.
(1)求证:△ABF≌△DCB
(2)若CD⊥AF,垂足为E,AB=10,∠C=60°,求EF的长.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)连接BE交AC于点F,若cos∠CAD= ,求 的值.
25.如图,⊙O是△ 的外接圆, 为直径,点 是⊙O外一点,且 ,连接 交 于点D,延长 交⊙O于点F.
(1)证明: = ;
(2)若 ,证明: 是⊙O的切线;
(3)在⑵的条件下,连接 交⊙O于点E,连接 ;若 ,求 的长.
第三章《圆》检测卷
(提升卷1)
第I卷(选择题)
一、选择题(本大题共10小题,每小题3分,共30分)
1.如图,点A、B、C是⊙O上的三个点,若∠AOB=82°,则∠C的度数为( )
A.82° B.38° C.24° D.41°
【答案】D
【解析】【解答】解: , ,
,
故答案为:D.
【分析】根据圆周角的性质:同弧所对的圆周角等于圆心角的一半求解即可。
2. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是
A.相交 B.相切 C.相离 D.无法确定
【答案】A
【解析】【解答】∵⊙O的半径为5,圆心O到直线的距离为3,∴直线l与⊙O的位置关系是相交.
故答案为:A.
【分析】设⊙O的半径为r,圆心O到直线的距离为d,当d<r时,直线与⊙O相交;当d=r时,直线与⊙O相切,当d>r时,直线与⊙O相离,据此判断即可.
3.如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且弧CE=弧CD,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
【答案】C
【解析】【解答】∵∠ACB=90°,∠A=56°,
∴∠ABC=34°,
∵ ,
∴∠COE =2∠ABC=68°,
又∵∠OCF=∠OEF=90°,
∴∠F=360°-90°-90°-68°=112°.
故答案为:C.
【分析】直接利用互余的性质再结合圆周角定理得出∠COE的度数,再利用四边形内角和定理得出答案.
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,OB=4,则AB的长为( )
A.2 B.4 C.6 D.4
【答案】D
【解析】【解答】解:∵⊙O的直径CD垂直弦AB于点E,
∴AB=2BE.∵CE=2,OB=4,∴OE=4﹣2=2,
∴BE= = = ,
∴AB= .
故答案为:D.
【分析】利用勾股定理求出BE,再根据垂径定理可证得AB=2BE,就可求出AB的长。
5.一个扇形的圆心角是120°,半径为3,则这个扇形的面积为( )
A. B. C. D.
【答案】C
【解析】【解答】解:由题意得,n=120°,r=3,
S扇形= = =3π,
故答案为:C.
【分析】直接利用扇形的面积公式计算即可.
6.如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
A.40° B.50° C.80° D.100°
【答案】C
【解析】【解答】解:∵在⊙O中,AB为直径,BC为弦,CD为切线,
∴∠OCD=90°,
∵∠BCD=50°,
∴∠OCB=40°,
∴∠AOC=80°,
故选C.
【分析】根据切线的性质得出∠OCD=90°,进而得出∠OCB=40°,再利用圆心角等于圆周角的2倍解答即可.
7.如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
A.50° B.60° C.70° D.80°
【答案】C
【解析】【解答】解:连接BC.
∵PA、PB切⊙O于A、B两点,
∴PA=PB,AC⊥PA,即∠PAC=90°,
∴∠PAB=∠PBA= = =70°,
∵∠BAC=∠PAC﹣∠PAB=90°﹣70°=20°,
∵AC是直径,
∴∠ABC=90°,
∴∠ACB=90°﹣∠ACB=90°﹣20°=70°.
故选C.
【分析】连接BC,根据切线长定理得到PA=PB,然后根据等腰三角形的性质求得∠PAB的度数,根据切线的性质得∠PAO=90°,则∠BAC即可求得,然后利用直径所对的圆周角是直角,以及直角三角形的性质求解.
8.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
【答案】C
【解析】【解答】解:作OH⊥CD于H,连结OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH= OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH= = ,
∴CD=2CH=2 .
故答案为:C.
【分析】作OH⊥CD于H,连结OC,如图,根据垂径定理得出HC=HD,在Rt△OPH中,根据含30°的直角三角形的边之间的关系得出OH= OP=1,在Rt△OHC中,根据勾股定理算出CH的长,从而得出答案。
9.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC= ,则图中阴影部分的面积是( )
A. B. C. D.
【答案】A
【解析】【解答】解:∵AB为直径,
∴∠ACB=90°,
∵AC=BC= ,
∴△ACB为等腰直角三角形,
∴OC⊥AB,
∴△AOC和△BOC都是等腰直角三角形,
∴S△AOC=S△BOC,OA= AC=1,∴S阴影部分=S扇形AOC= .
故选A.
【分析】先利用圆周角定理得到∠ACB=90°,则可判断△ACB为等腰直角三角形,接着判断△AOC和△BOC都是等腰直角三角形,于是得到S△AOC=S△BOC,然后根据扇形的面积公式计算图中阴影部分的面积.本题考查了扇形面积的计算:圆面积公式:S=πr2,(2)扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.求阴影面积常用的方法:①直接用公式法; ②和差法; ③割补法.求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.
10.如图,已知⊙P与坐标轴交于点A,O,B,点C在⊙P上,且∠ACO=60°,若点B的坐标为(0,3),则弧OA的长为( )
A.2π B.3π C. π D.2 π
【答案】A
【解析】【解答】解:如图,连接AB、OP,
∴AB为P的直径,
∴弧OA的长
故答案为:A.
【分析】作辅助线,先根据圆周角定理可知:AB为⊙P的直径,由圆心角和圆周角的关系可得: 得出AB=6, 根据弧长公式可得结论.
第II卷(非选择题)
二、填空题(本大题共7小题,每小题4分,共28分)
11.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)
【答案】
【解析】【解答】解:∵∠ACB=90°,AC=1,AB=2,
∴∠ABC=30°,
∴∠A=60°,,
又∵AC=1,
∴弧CD的长为 = ,
故答案为: .
【分析】弧长=,根据直角三角形中,30度角所对的直角边等于斜边的一半可得∠ABC=30°,则∠A=60°,将n和r的值代入弧长公式计算即可求解。
12.一条弧所对的圆心角为,弧长等于,则这条弧的半径为 .
【答案】9cm
【解析】【解答】解:∵
∴
故答案为:9cm
【分析】根据 一条弧所对的圆心角为,弧长等于, 利用弧长公式计算求解即可。
13.如图,已知PA、PB分别切⊙O于A、B点,C为优弧ACB上除A、B一点,若∠P=70°,则∠ACB的大小为 度.
【答案】55
【解析】【解答】解:如图,连接
PA、PB分别切⊙O于A、B点,
故答案为:55.
【分析】连接 由AP、BP为圆的切线可得∠OAP=∠OBP=90°,再根据四边形内角和为360°可得∠AOB的度数,由同弧所对的圆周角是所对圆心角的一半可得结果.
14.如图,正八边形ABCDEFGH的半径为2,它的面积为
【答案】8
【解析】【解答】解:连接AO,BO,CO,AC,
∵正八边形ABCDEFGH的半径为2,
∴AO=BO=CO=2,∠AOB=∠BOC= =45°,
∴∠AOC=90°,
∴AC=2 ,此时AC与BO垂直,
∴S四边形AOCB= BO×AC= ×2×2 =2 ,
∴正八边形面积为:2 × =8 .
故答案为:8 .
【分析】首先根据正八边形的性质得出AO=BO=CO=2,∠AOB=∠BOC= =45°,进而得出AC的长,即可得出S四边形AOCB的面积,进而得出答案.
15.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=12,且AC+BC=10,则AB的长为 .
【答案】
【解析】【解答】解:由勾股定理得,AC2+BC2=AB2,
∵S1+S2=12,
∴ ,
∴AC×BC=24,
∵AC+BC=10.
∴AB=
故答案为: .
【分析】根据勾股定理得到AC2+BC2=AB2,根据扇形面积公式、完全平方公式计算即可.
16.如图, 是半径为 的⊙ 的直径, 是圆上异于 , 的任意一点, 的平分线交⊙ 于点 ,连接 和 ,△ 的中位线所在的直线与⊙ 相交于点 、 ,则 的长是
【答案】4
【解析】【解答】解:如图所示:
∵PC是∠APB的角平分线,
∴∠APC=∠CPB,
∴=;
∴AC=BC;
∵AB是直径,
∴∠ACB=90 .
即△ABC是等腰直角三角形。
连接OC,交EF于点D,则OC⊥AB;
∵MN是△ABC的中位线,
∴MN∥AB;
∴OC⊥EF,OD= OC=2.
连接OE,根据勾股定理,得:DE= =2 ,
∴EF=2ED=4 .
故答案为:4 .
【分析】先根据角平分线的性质得出∠APC=∠CPB,在同一个圆内相等的圆周角对应的弧长和弦长相等,可得出AC=BC,连接OC则OC⊥AB,根据垂径定理结合中位线可得出OD= OC=2,再在内根据勾股定理求出ED的长度,EF的长度是ED长度的2倍。
17.如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在 上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是 .
【答案】2 π
【解析】【解答】解:如图,由此BO交⊙O于F,取 的中点H,连接FH、HB、BD.
易知△FHB是等腰直角三角形,HF=HB,∠FHB=90°,
∵∠FDB=45°= ∠FHB,
∴点D在⊙H上运动,轨迹是 (图中红线),
易知∠HFG=∠HGF=15°,
∴∠FHG=150°,
∴∠GHB=120°,易知HB=3 ,
∴点D的运动轨迹的长为 =2 π.
故答案为2 π.
【分析】由此BO交⊙O于F,取 弧B F 的中点H,连接FH、HB、BD.可证得△FHB是等腰直角三角形,可以得到HF=HB,∠FHB=90°,就可以求出∠FDB的度数,进而可知道点D就是在⊙H上运动,它的运动轨迹就是弧GB的长,∠AOB=120°推出∠AOF=60°,得出△AOF是等边三角形,易求得∠∠HFG=∠HGF=15°,就可得∠FHG的度数,从而求出圆心角∠GHB的度数,在Rt△BHF中可以求出半径HB的长,利用弧长公式就可以求得点D的运动轨迹的长。
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,过点D作DE∥BC,交⊙O于点E,连接CE.
求证:四边形DBCE是平行四边形.
【答案】证明:∵AC=BC,∴∠BAC=∠B.
∵DE∥BC,∴∠ADE=∠B. ∴∠ADE=∠BAC
又∵在⊙O中,∠BAC=∠CED,
∴∠ADE=∠CED,∴BD∥CE.
又∵DF∥BC,
∴四边形DBCF是平行四边形.
【解析】【分析】由AC=BC,可得∠BAC=∠B,由DE∥BC,可得∠ADE=∠B. 由等量代换可得∠ADE=∠BAC
根据同弧所对的圆周角相等,可得∠BAC=∠CED,由等量代换可得∠ADE=∠CED,可得BD∥CE,根据两组对边分别平行的四边形是平行四边形即证.
19.如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
【答案】解:∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm,
∴BC2=AB2﹣AC2=102﹣62=64,
∴BC= =8(cm),
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴ ,
∴AD=BD ,
又在Rt△ABD中,AD2+BD2=AB2,
∴AD2+BD2=102,
∴AD=BD= =5 (cm).
【解析】【分析】先求出 BC= =8(cm), 再求出 AD=BD , 最后利用勾股定理计算求解即可。
20.已知AB为 的直径,EF切 于点D,过点B作 于点H交 于点C,连接BD.
(1)如图①,若 ,求 的大小;
(2)如图②,若C为弧BD的中点,求 的大小.
【答案】(1)如图,连接OD.
由切线的性质结合题意可知 ,
∴ ,
∴ .
∵ ,
∴ .
∵ ,
∴ ,
∴ .
∴ .
(2)如图,连接OD、OC、CD.
∵OC=OD,
∴ .
∵ ,即 ,
∴ ,
∵ ,
∴ .
∵C为 中点,
∴ ,
由(1)可知 ,
∴ ,
∵ ,
∴ .
∴ .
【解析】【分析】(1)先求出 ,再求出 ,最后计算求解即可;
(2)先求出 , 再求出 ,最后计算求解即可。
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.
(1)求证:DE是⊙O的切线;
(2)当DE=1,∠C=30°时,求图中阴影部分的面积.
【答案】(1)解:连接OD,
∵AB是⊙O的直径,D是AC的中点,
∴OD是△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∵点D在圆上,
∴DE为⊙O的切线.
(2)解:∵∠C=30°,DE=1,∠DEC=90°,
∴DC=2,
∵OD∥BC,
∴∠ODA=30°,
∵OD=OA,
∴∠OAD=∠ODA=30°,
∴∠AOD=120°,
∴OA= ,
∴阴影部分面积S= ﹣ ×2× = ﹣ .
【解析】【分析】(1)根据中位线的性质,可得出OD⊥DE,得知DE为圆的切线。
(2)根据OA的长度以及扇形面积的公式求出扇形面积,再减去三角形的面积可得出阴影部分面积。
22.如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.
【答案】(1)证明:∵圆心O在BC上,
∴BC是圆O的直径,
∴∠BAC=90°,
连接OD,
∵AD平分∠BAC,
∴∠BAC=2∠DAC,
∵∠DOC=2∠DAC,
∴∠DOC=∠BAC=90°,即OD⊥BC,
∵PD∥BC,
∴OD⊥PD,
∵OD为圆O的半径,
∴PD是圆O的切线;
(2)证明:∵PD∥BC,
∴∠P=∠ABC,
∵∠ABC=∠ADC,
∴∠P=∠ADC,
∵∠PBD+∠ABD=180°,∠ACD+∠ABD=180°,
∴∠PBD=∠ACD,
∴△PBD∽△DCA;
(3)解:∵△ABC为直角三角形,
∴BC2=AB2+AC2=62+82=100,
∴BC=10,
∵OD垂直平分BC,
∴DB=DC,
∵BC为圆O的直径,
∴∠BDC=90°,
在Rt△DBC中,DB2+DC2=BC2,即2DC2=BC2=100,
∴DC=DB=5 ,
∵△PBD∽△DCA,
∴
则PB= = = .
【解析】【分析】(1) 连接OD, 根据直径所对的圆周角是直角得出 ∠BAC=90°, 根据角平分线的定义得出 ∠BAC=2∠DAC, 根据同弧所对的圆心角等于圆周角的2倍得出 ∠DOC=2∠DAC, 故 ∠DOC=∠BAC=90°,即OD⊥BC, 根据平行线的性质得出 OD⊥PD, 根据垂直于半径的外端点的直线是圆的切线得出 PD是圆O的切线;
(2)根据二直线平行,同位角相等得出 ∠P=∠ABC, 根据同弧所对的圆周角相等得出 ∠ABC=∠ADC, 故 ∠P=∠ADC, 根据同角的补角相等得出 ∠PBD=∠ACD, 根据有两组角对应相等的两个三角形相似得出 △PBD∽△DCA;
(3)首先根据勾股定理算出BC的长,根据线段垂直平分线上的点到线段两个端点的距离相等得出 DB=DC, 根据直径所对的圆周角是直角得出 ∠BDC=90°, 在Rt△DBC中 ,根据等腰直角三角形的性质得出 DC=DB=5 , 然后根据相似三角形对应边成比例得出 ,根据比例式即可求出PB的长。
23.如图,⊙O中,AB、CD是⊙O的直径,F是⊙O上一点,连接BC、BF,若点B是弧CF的中点.
(1)求证:△ABF≌△DCB
(2)若CD⊥AF,垂足为E,AB=10,∠C=60°,求EF的长.
【答案】(1)证明:
∵AB、CD是⊙O的直径,
∴AB=CD,∠F=∠CBD=90°,
点B是弧CF的中点,
∴BF=BC,
在Rt△ABF≌Rt△DCB中,
∴Rt△ABF≌Rt△DCB(HL)
(2)∵∠C=60°,
∴∠ABF=60°,
∴∠A=30°,
∴BF=AB,
∵AB=10,
∴BF=5,
在Rt△ABF中,AF==5
∵CD⊥AF,
∴EF=AF=.
【解析】【分析】(1)根据点B是弧CF的中点,得BF=BC,根据HL即可得出△ABF≌△DCB;
(2)易得BC=5,则BF=5,在Rt△ABF中,根据勾股定理得出AF,根据CD⊥AF,得出EF的值即可.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)连接BE交AC于点F,若cos∠CAD= ,求 的值.
【答案】(1)证明:连接OC,
∵CD是⊙O的切线,
∴CD⊥OC,
又∵CD⊥AD,
∴AD∥OC,
∴∠CAD=∠ACO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠CAD=∠CAO,
即AC平分∠DAB
(2)解:连接BE、BC、OC,BE交AC于F交OC于H.
∵AB是直径,
∴∠AEB=∠DEH=∠D=∠DCH=90°,
∴四边形DEHC是矩形,
∴∠EHC=90°即OC⊥EB,
∴DC=EH=HB,DE=HC,
∵cos∠CAD= = ,设AD=4a,AC=5a,则DC=EH=HB=3a,
∵cos∠CAB= = ,
∴AB= a,BC= a,
在RT△CHB中,CH= = a,
∴DE=CH= a,AE= = a,
∵EF∥CD,
∴ = =
【解析】【分析】(1)连接OC,根据切线的性质和已知求出OC∥AD,求出∠OCA=∠CAO=∠DAC,即可得出答案;(2)连接BE、BC、OC,BE交AC于F交OC于H,根据cos∠CAD= = ,设AD=4a,AC=5a,则DC=EH=HB=3a,根据cos∠CAB= = ,求出AB、BC,再根据勾股定理求出CH,由此即可解决问题;
25.如图,⊙O是△ 的外接圆, 为直径,点 是⊙O外一点,且 ,连接 交 于点D,延长 交⊙O于点F.
(1)证明: = ;
(2)若 ,证明: 是⊙O的切线;
(3)在⑵的条件下,连接 交⊙O于点E,连接 ;若 ,求 的长.
【答案】(1)证明:如图,连接CO,
在△PCO和△PAO中,
∴△PCO≌△PAO(SSS),
∴∠CPO=∠APO,即PO为∠APC的角平分线,
∵PA=PC,
∴CD=AD,PF⊥AC,
∵AC为⊙O的弦,PF过圆心O,
∴F为优弧 中点,
∴ = ,
(2)证明:∵AB是⊙O的直径,且弦AB所对圆周角为∠ACB,
∴∠ACB=90°,
∵tan∠ABC= ,
∴sin∠ABC= ,cos∠ABC= ,
设⊙O的半径为r,则AB=2r,
∴BC=ABcos∠ABC= ,AC=ABsin∠ABC= ,
∴ ,
∵PA=PC= AB,
∴PA=PC= ,
∴ ,
∴PO=PD+OD=3r,
∴ ,即PA⊥OA,
又∵OA是⊙O半径,
∴PA是⊙O的切线;
(3)解:由(2)可得 ,
∴ ,
在Rt△PBA中, ,连接AE,可得∠AEB=90°,
∴∠PEA=∠PAB=90°,又∠APE=∠APB,
∴△PEA∽△PAB,
∴ ,
∴ ,
过E作EN⊥PD于N,过B作BH⊥PF于H,如图所示,
∴∠BCD=∠CDF=∠BHD=90°,
∴四边形BCDH是矩形,
∴BH=CD= ,
在Rt△BPH中,sin∠BPH= ,
在Rt△PEN中,sin∠BPH= ,∴ ,
∴ ,
∴ND=PD-PN= ,
在Rt△NED中,DE= ,
∵ ,
∴DE= .
【解析】【分析】(1)连接CO,易证△PCO≌△PAO,得PO为∠APC的角平分线,根据条件证出F为优弧 中点,即可证明 = ;(2)因为AB是直径,所以∠ACB=90°,由tan∠ABC= 可求得∠ABC的正弦和余弦,设⊙O的半径为r,则AB=2r,根据三角函数表示出BC,AC的长度,由勾股定理表示出OD的长度,易得PA=PC= , ,PO=PD+OD=3r,由 可得PA⊥OA,即可证明 是⊙ 的切线;(3)连接AE,过E作EN⊥PD于N,过B作BH⊥PF于H,由(2)可得, ,PB= ,证出△PEA∽△PAB,可得 ,证出四边形BCDH是矩形,得BH=CD= ,在Rt△BPH和Rt△PEN中表示出sin∠BPH,可得 , ,ND=PD-PN= ,在Rt△NED中,DE= ,代入r=3即可
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第三章《圆》检测卷
(提升卷1)
第I卷(选择题)
一、选择题(本大题共10小题,每小题3分,共30分)
1.如图,点A、B、C是⊙O上的三个点,若∠AOB=82°,则∠C的度数为( )
A.82° B.38° C.24° D.41°
2. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是
A.相交 B.相切 C.相离 D.无法确定
3.如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且弧CE=弧CD,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,OB=4,则AB的长为( )
A.2 B.4 C.6 D.4
5.一个扇形的圆心角是120°,半径为3,则这个扇形的面积为( )
A. B. C. D.
6.如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
A.40° B.50° C.80° D.100°
7.如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
A.50° B.60° C.70° D.80°
8.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
9.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC= ,则图中阴影部分的面积是( )
A. B. C. D.
10.如图,已知⊙P与坐标轴交于点A,O,B,点C在⊙P上,且∠ACO=60°,若点B的坐标为(0,3),则弧OA的长为( )
A.2π B.3π C. π D.2 π
第II卷(非选择题)
二、填空题(本大题共7小题,每小题4分,共28分)
11.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)
12.一条弧所对的圆心角为,弧长等于,则这条弧的半径为 .
13.如图,已知PA、PB分别切⊙O于A、B点,C为优弧ACB上除A、B一点,若∠P=70°,则∠ACB的大小为 度.
14.如图,正八边形ABCDEFGH的半径为2,它的面积为
15.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=12,且AC+BC=10,则AB的长为 .
16.如图, 是半径为 的⊙ 的直径, 是圆上异于 , 的任意一点, 的平分线交⊙ 于点 ,连接 和 ,△ 的中位线所在的直线与⊙ 相交于点 、 ,则 的长是
17.如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在 上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是 .
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,过点D作DE∥BC,交⊙O于点E,连接CE.
求证:四边形DBCE是平行四边形.
19.如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
20.已知AB为 的直径,EF切 于点D,过点B作 于点H交 于点C,连接BD.
(1)如图①,若 ,求 的大小;
(2)如图②,若C为弧BD的中点,求 的大小.
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.
(1)求证:DE是⊙O的切线;
(2)当DE=1,∠C=30°时,求图中阴影部分的面积.
22.如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.
23.如图,⊙O中,AB、CD是⊙O的直径,F是⊙O上一点,连接BC、BF,若点B是弧CF的中点.
(1)求证:△ABF≌△DCB
(2)若CD⊥AF,垂足为E,AB=10,∠C=60°,求EF的长.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)连接BE交AC于点F,若cos∠CAD= ,求 的值.
25.如图,⊙O是△ 的外接圆, 为直径,点 是⊙O外一点,且 ,连接 交 于点D,延长 交⊙O于点F.
(1)证明: = ;
(2)若 ,证明: 是⊙O的切线;
(3)在⑵的条件下,连接 交⊙O于点E,连接 ;若 ,求 的长.
第三章《圆》检测卷
(提升卷1)
第I卷(选择题)
一、选择题(本大题共10小题,每小题3分,共30分)
1.如图,点A、B、C是⊙O上的三个点,若∠AOB=82°,则∠C的度数为( )
A.82° B.38° C.24° D.41°
【答案】D
【解析】【解答】解: , ,
,
故答案为:D.
【分析】根据圆周角的性质:同弧所对的圆周角等于圆心角的一半求解即可。
2. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是
A.相交 B.相切 C.相离 D.无法确定
【答案】A
【解析】【解答】∵⊙O的半径为5,圆心O到直线的距离为3,∴直线l与⊙O的位置关系是相交.
故答案为:A.
【分析】设⊙O的半径为r,圆心O到直线的距离为d,当d<r时,直线与⊙O相交;当d=r时,直线与⊙O相切,当d>r时,直线与⊙O相离,据此判断即可.
3.如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且弧CE=弧CD,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
【答案】C
【解析】【解答】∵∠ACB=90°,∠A=56°,
∴∠ABC=34°,
∵ ,
∴∠COE =2∠ABC=68°,
又∵∠OCF=∠OEF=90°,
∴∠F=360°-90°-90°-68°=112°.
故答案为:C.
【分析】直接利用互余的性质再结合圆周角定理得出∠COE的度数,再利用四边形内角和定理得出答案.
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,OB=4,则AB的长为( )
A.2 B.4 C.6 D.4
【答案】D
【解析】【解答】解:∵⊙O的直径CD垂直弦AB于点E,
∴AB=2BE.∵CE=2,OB=4,∴OE=4﹣2=2,
∴BE= = = ,
∴AB= .
故答案为:D.
【分析】利用勾股定理求出BE,再根据垂径定理可证得AB=2BE,就可求出AB的长。
5.一个扇形的圆心角是120°,半径为3,则这个扇形的面积为( )
A. B. C. D.
【答案】C
【解析】【解答】解:由题意得,n=120°,r=3,
S扇形= = =3π,
故答案为:C.
【分析】直接利用扇形的面积公式计算即可.
6.如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
A.40° B.50° C.80° D.100°
【答案】C
【解析】【解答】解:∵在⊙O中,AB为直径,BC为弦,CD为切线,
∴∠OCD=90°,
∵∠BCD=50°,
∴∠OCB=40°,
∴∠AOC=80°,
故选C.
【分析】根据切线的性质得出∠OCD=90°,进而得出∠OCB=40°,再利用圆心角等于圆周角的2倍解答即可.
7.如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
A.50° B.60° C.70° D.80°
【答案】C
【解析】【解答】解:连接BC.
∵PA、PB切⊙O于A、B两点,
∴PA=PB,AC⊥PA,即∠PAC=90°,
∴∠PAB=∠PBA= = =70°,
∵∠BAC=∠PAC﹣∠PAB=90°﹣70°=20°,
∵AC是直径,
∴∠ABC=90°,
∴∠ACB=90°﹣∠ACB=90°﹣20°=70°.
故选C.
【分析】连接BC,根据切线长定理得到PA=PB,然后根据等腰三角形的性质求得∠PAB的度数,根据切线的性质得∠PAO=90°,则∠BAC即可求得,然后利用直径所对的圆周角是直角,以及直角三角形的性质求解.
8.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
【答案】C
【解析】【解答】解:作OH⊥CD于H,连结OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH= OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH= = ,
∴CD=2CH=2 .
故答案为:C.
【分析】作OH⊥CD于H,连结OC,如图,根据垂径定理得出HC=HD,在Rt△OPH中,根据含30°的直角三角形的边之间的关系得出OH= OP=1,在Rt△OHC中,根据勾股定理算出CH的长,从而得出答案。
9.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC= ,则图中阴影部分的面积是( )
A. B. C. D.
【答案】A
【解析】【解答】解:∵AB为直径,
∴∠ACB=90°,
∵AC=BC= ,
∴△ACB为等腰直角三角形,
∴OC⊥AB,
∴△AOC和△BOC都是等腰直角三角形,
∴S△AOC=S△BOC,OA= AC=1,∴S阴影部分=S扇形AOC= .
故选A.
【分析】先利用圆周角定理得到∠ACB=90°,则可判断△ACB为等腰直角三角形,接着判断△AOC和△BOC都是等腰直角三角形,于是得到S△AOC=S△BOC,然后根据扇形的面积公式计算图中阴影部分的面积.本题考查了扇形面积的计算:圆面积公式:S=πr2,(2)扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.求阴影面积常用的方法:①直接用公式法; ②和差法; ③割补法.求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.
10.如图,已知⊙P与坐标轴交于点A,O,B,点C在⊙P上,且∠ACO=60°,若点B的坐标为(0,3),则弧OA的长为( )
A.2π B.3π C. π D.2 π
【答案】A
【解析】【解答】解:如图,连接AB、OP,
∴AB为P的直径,
∴弧OA的长
故答案为:A.
【分析】作辅助线,先根据圆周角定理可知:AB为⊙P的直径,由圆心角和圆周角的关系可得: 得出AB=6, 根据弧长公式可得结论.
第II卷(非选择题)
二、填空题(本大题共7小题,每小题4分,共28分)
11.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)
【答案】
【解析】【解答】解:∵∠ACB=90°,AC=1,AB=2,
∴∠ABC=30°,
∴∠A=60°,,
又∵AC=1,
∴弧CD的长为 = ,
故答案为: .
【分析】弧长=,根据直角三角形中,30度角所对的直角边等于斜边的一半可得∠ABC=30°,则∠A=60°,将n和r的值代入弧长公式计算即可求解。
12.一条弧所对的圆心角为,弧长等于,则这条弧的半径为 .
【答案】9cm
【解析】【解答】解:∵
∴
故答案为:9cm
【分析】根据 一条弧所对的圆心角为,弧长等于, 利用弧长公式计算求解即可。
13.如图,已知PA、PB分别切⊙O于A、B点,C为优弧ACB上除A、B一点,若∠P=70°,则∠ACB的大小为 度.
【答案】55
【解析】【解答】解:如图,连接
PA、PB分别切⊙O于A、B点,
故答案为:55.
【分析】连接 由AP、BP为圆的切线可得∠OAP=∠OBP=90°,再根据四边形内角和为360°可得∠AOB的度数,由同弧所对的圆周角是所对圆心角的一半可得结果.
14.如图,正八边形ABCDEFGH的半径为2,它的面积为
【答案】8
【解析】【解答】解:连接AO,BO,CO,AC,
∵正八边形ABCDEFGH的半径为2,
∴AO=BO=CO=2,∠AOB=∠BOC= =45°,
∴∠AOC=90°,
∴AC=2 ,此时AC与BO垂直,
∴S四边形AOCB= BO×AC= ×2×2 =2 ,
∴正八边形面积为:2 × =8 .
故答案为:8 .
【分析】首先根据正八边形的性质得出AO=BO=CO=2,∠AOB=∠BOC= =45°,进而得出AC的长,即可得出S四边形AOCB的面积,进而得出答案.
15.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=12,且AC+BC=10,则AB的长为 .
【答案】
【解析】【解答】解:由勾股定理得,AC2+BC2=AB2,
∵S1+S2=12,
∴ ,
∴AC×BC=24,
∵AC+BC=10.
∴AB=
故答案为: .
【分析】根据勾股定理得到AC2+BC2=AB2,根据扇形面积公式、完全平方公式计算即可.
16.如图, 是半径为 的⊙ 的直径, 是圆上异于 , 的任意一点, 的平分线交⊙ 于点 ,连接 和 ,△ 的中位线所在的直线与⊙ 相交于点 、 ,则 的长是
【答案】4
【解析】【解答】解:如图所示:
∵PC是∠APB的角平分线,
∴∠APC=∠CPB,
∴=;
∴AC=BC;
∵AB是直径,
∴∠ACB=90 .
即△ABC是等腰直角三角形。
连接OC,交EF于点D,则OC⊥AB;
∵MN是△ABC的中位线,
∴MN∥AB;
∴OC⊥EF,OD= OC=2.
连接OE,根据勾股定理,得:DE= =2 ,
∴EF=2ED=4 .
故答案为:4 .
【分析】先根据角平分线的性质得出∠APC=∠CPB,在同一个圆内相等的圆周角对应的弧长和弦长相等,可得出AC=BC,连接OC则OC⊥AB,根据垂径定理结合中位线可得出OD= OC=2,再在内根据勾股定理求出ED的长度,EF的长度是ED长度的2倍。
17.如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在 上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是 .
【答案】2 π
【解析】【解答】解:如图,由此BO交⊙O于F,取 的中点H,连接FH、HB、BD.
易知△FHB是等腰直角三角形,HF=HB,∠FHB=90°,
∵∠FDB=45°= ∠FHB,
∴点D在⊙H上运动,轨迹是 (图中红线),
易知∠HFG=∠HGF=15°,
∴∠FHG=150°,
∴∠GHB=120°,易知HB=3 ,
∴点D的运动轨迹的长为 =2 π.
故答案为2 π.
【分析】由此BO交⊙O于F,取 弧B F 的中点H,连接FH、HB、BD.可证得△FHB是等腰直角三角形,可以得到HF=HB,∠FHB=90°,就可以求出∠FDB的度数,进而可知道点D就是在⊙H上运动,它的运动轨迹就是弧GB的长,∠AOB=120°推出∠AOF=60°,得出△AOF是等边三角形,易求得∠∠HFG=∠HGF=15°,就可得∠FHG的度数,从而求出圆心角∠GHB的度数,在Rt△BHF中可以求出半径HB的长,利用弧长公式就可以求得点D的运动轨迹的长。
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,过点D作DE∥BC,交⊙O于点E,连接CE.
求证:四边形DBCE是平行四边形.
【答案】证明:∵AC=BC,∴∠BAC=∠B.
∵DE∥BC,∴∠ADE=∠B. ∴∠ADE=∠BAC
又∵在⊙O中,∠BAC=∠CED,
∴∠ADE=∠CED,∴BD∥CE.
又∵DF∥BC,
∴四边形DBCF是平行四边形.
【解析】【分析】由AC=BC,可得∠BAC=∠B,由DE∥BC,可得∠ADE=∠B. 由等量代换可得∠ADE=∠BAC
根据同弧所对的圆周角相等,可得∠BAC=∠CED,由等量代换可得∠ADE=∠CED,可得BD∥CE,根据两组对边分别平行的四边形是平行四边形即证.
19.如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
【答案】解:∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm,
∴BC2=AB2﹣AC2=102﹣62=64,
∴BC= =8(cm),
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴ ,
∴AD=BD ,
又在Rt△ABD中,AD2+BD2=AB2,
∴AD2+BD2=102,
∴AD=BD= =5 (cm).
【解析】【分析】先求出 BC= =8(cm), 再求出 AD=BD , 最后利用勾股定理计算求解即可。
20.已知AB为 的直径,EF切 于点D,过点B作 于点H交 于点C,连接BD.
(1)如图①,若 ,求 的大小;
(2)如图②,若C为弧BD的中点,求 的大小.
【答案】(1)如图,连接OD.
由切线的性质结合题意可知 ,
∴ ,
∴ .
∵ ,
∴ .
∵ ,
∴ ,
∴ .
∴ .
(2)如图,连接OD、OC、CD.
∵OC=OD,
∴ .
∵ ,即 ,
∴ ,
∵ ,
∴ .
∵C为 中点,
∴ ,
由(1)可知 ,
∴ ,
∵ ,
∴ .
∴ .
【解析】【分析】(1)先求出 ,再求出 ,最后计算求解即可;
(2)先求出 , 再求出 ,最后计算求解即可。
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.
(1)求证:DE是⊙O的切线;
(2)当DE=1,∠C=30°时,求图中阴影部分的面积.
【答案】(1)解:连接OD,
∵AB是⊙O的直径,D是AC的中点,
∴OD是△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∵点D在圆上,
∴DE为⊙O的切线.
(2)解:∵∠C=30°,DE=1,∠DEC=90°,
∴DC=2,
∵OD∥BC,
∴∠ODA=30°,
∵OD=OA,
∴∠OAD=∠ODA=30°,
∴∠AOD=120°,
∴OA= ,
∴阴影部分面积S= ﹣ ×2× = ﹣ .
【解析】【分析】(1)根据中位线的性质,可得出OD⊥DE,得知DE为圆的切线。
(2)根据OA的长度以及扇形面积的公式求出扇形面积,再减去三角形的面积可得出阴影部分面积。
22.如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.
【答案】(1)证明:∵圆心O在BC上,
∴BC是圆O的直径,
∴∠BAC=90°,
连接OD,
∵AD平分∠BAC,
∴∠BAC=2∠DAC,
∵∠DOC=2∠DAC,
∴∠DOC=∠BAC=90°,即OD⊥BC,
∵PD∥BC,
∴OD⊥PD,
∵OD为圆O的半径,
∴PD是圆O的切线;
(2)证明:∵PD∥BC,
∴∠P=∠ABC,
∵∠ABC=∠ADC,
∴∠P=∠ADC,
∵∠PBD+∠ABD=180°,∠ACD+∠ABD=180°,
∴∠PBD=∠ACD,
∴△PBD∽△DCA;
(3)解:∵△ABC为直角三角形,
∴BC2=AB2+AC2=62+82=100,
∴BC=10,
∵OD垂直平分BC,
∴DB=DC,
∵BC为圆O的直径,
∴∠BDC=90°,
在Rt△DBC中,DB2+DC2=BC2,即2DC2=BC2=100,
∴DC=DB=5 ,
∵△PBD∽△DCA,
∴
则PB= = = .
【解析】【分析】(1) 连接OD, 根据直径所对的圆周角是直角得出 ∠BAC=90°, 根据角平分线的定义得出 ∠BAC=2∠DAC, 根据同弧所对的圆心角等于圆周角的2倍得出 ∠DOC=2∠DAC, 故 ∠DOC=∠BAC=90°,即OD⊥BC, 根据平行线的性质得出 OD⊥PD, 根据垂直于半径的外端点的直线是圆的切线得出 PD是圆O的切线;
(2)根据二直线平行,同位角相等得出 ∠P=∠ABC, 根据同弧所对的圆周角相等得出 ∠ABC=∠ADC, 故 ∠P=∠ADC, 根据同角的补角相等得出 ∠PBD=∠ACD, 根据有两组角对应相等的两个三角形相似得出 △PBD∽△DCA;
(3)首先根据勾股定理算出BC的长,根据线段垂直平分线上的点到线段两个端点的距离相等得出 DB=DC, 根据直径所对的圆周角是直角得出 ∠BDC=90°, 在Rt△DBC中 ,根据等腰直角三角形的性质得出 DC=DB=5 , 然后根据相似三角形对应边成比例得出 ,根据比例式即可求出PB的长。
23.如图,⊙O中,AB、CD是⊙O的直径,F是⊙O上一点,连接BC、BF,若点B是弧CF的中点.
(1)求证:△ABF≌△DCB
(2)若CD⊥AF,垂足为E,AB=10,∠C=60°,求EF的长.
【答案】(1)证明:
∵AB、CD是⊙O的直径,
∴AB=CD,∠F=∠CBD=90°,
点B是弧CF的中点,
∴BF=BC,
在Rt△ABF≌Rt△DCB中,
∴Rt△ABF≌Rt△DCB(HL)
(2)∵∠C=60°,
∴∠ABF=60°,
∴∠A=30°,
∴BF=AB,
∵AB=10,
∴BF=5,
在Rt△ABF中,AF==5
∵CD⊥AF,
∴EF=AF=.
【解析】【分析】(1)根据点B是弧CF的中点,得BF=BC,根据HL即可得出△ABF≌△DCB;
(2)易得BC=5,则BF=5,在Rt△ABF中,根据勾股定理得出AF,根据CD⊥AF,得出EF的值即可.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)连接BE交AC于点F,若cos∠CAD= ,求 的值.
【答案】(1)证明:连接OC,
∵CD是⊙O的切线,
∴CD⊥OC,
又∵CD⊥AD,
∴AD∥OC,
∴∠CAD=∠ACO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠CAD=∠CAO,
即AC平分∠DAB
(2)解:连接BE、BC、OC,BE交AC于F交OC于H.
∵AB是直径,
∴∠AEB=∠DEH=∠D=∠DCH=90°,
∴四边形DEHC是矩形,
∴∠EHC=90°即OC⊥EB,
∴DC=EH=HB,DE=HC,
∵cos∠CAD= = ,设AD=4a,AC=5a,则DC=EH=HB=3a,
∵cos∠CAB= = ,
∴AB= a,BC= a,
在RT△CHB中,CH= = a,
∴DE=CH= a,AE= = a,
∵EF∥CD,
∴ = =
【解析】【分析】(1)连接OC,根据切线的性质和已知求出OC∥AD,求出∠OCA=∠CAO=∠DAC,即可得出答案;(2)连接BE、BC、OC,BE交AC于F交OC于H,根据cos∠CAD= = ,设AD=4a,AC=5a,则DC=EH=HB=3a,根据cos∠CAB= = ,求出AB、BC,再根据勾股定理求出CH,由此即可解决问题;
25.如图,⊙O是△ 的外接圆, 为直径,点 是⊙O外一点,且 ,连接 交 于点D,延长 交⊙O于点F.
(1)证明: = ;
(2)若 ,证明: 是⊙O的切线;
(3)在⑵的条件下,连接 交⊙O于点E,连接 ;若 ,求 的长.
【答案】(1)证明:如图,连接CO,
在△PCO和△PAO中,
∴△PCO≌△PAO(SSS),
∴∠CPO=∠APO,即PO为∠APC的角平分线,
∵PA=PC,
∴CD=AD,PF⊥AC,
∵AC为⊙O的弦,PF过圆心O,
∴F为优弧 中点,
∴ = ,
(2)证明:∵AB是⊙O的直径,且弦AB所对圆周角为∠ACB,
∴∠ACB=90°,
∵tan∠ABC= ,
∴sin∠ABC= ,cos∠ABC= ,
设⊙O的半径为r,则AB=2r,
∴BC=ABcos∠ABC= ,AC=ABsin∠ABC= ,
∴ ,
∵PA=PC= AB,
∴PA=PC= ,
∴ ,
∴PO=PD+OD=3r,
∴ ,即PA⊥OA,
又∵OA是⊙O半径,
∴PA是⊙O的切线;
(3)解:由(2)可得 ,
∴ ,
在Rt△PBA中, ,连接AE,可得∠AEB=90°,
∴∠PEA=∠PAB=90°,又∠APE=∠APB,
∴△PEA∽△PAB,
∴ ,
∴ ,
过E作EN⊥PD于N,过B作BH⊥PF于H,如图所示,
∴∠BCD=∠CDF=∠BHD=90°,
∴四边形BCDH是矩形,
∴BH=CD= ,
在Rt△BPH中,sin∠BPH= ,
在Rt△PEN中,sin∠BPH= ,∴ ,
∴ ,
∴ND=PD-PN= ,
在Rt△NED中,DE= ,
∵ ,
∴DE= .
【解析】【分析】(1)连接CO,易证△PCO≌△PAO,得PO为∠APC的角平分线,根据条件证出F为优弧 中点,即可证明 = ;(2)因为AB是直径,所以∠ACB=90°,由tan∠ABC= 可求得∠ABC的正弦和余弦,设⊙O的半径为r,则AB=2r,根据三角函数表示出BC,AC的长度,由勾股定理表示出OD的长度,易得PA=PC= , ,PO=PD+OD=3r,由 可得PA⊥OA,即可证明 是⊙ 的切线;(3)连接AE,过E作EN⊥PD于N,过B作BH⊥PF于H,由(2)可得, ,PB= ,证出△PEA∽△PAB,可得 ,证出四边形BCDH是矩形,得BH=CD= ,在Rt△BPH和Rt△PEN中表示出sin∠BPH,可得 , ,ND=PD-PN= ,在Rt△NED中,DE= ,代入r=3即可
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
