2022届高三各地一模试卷专题汇编——立体几何4
文档属性
| 名称 | 2022届高三各地一模试卷专题汇编——立体几何4 |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 09:35:08 | ||
图片预览

文档简介
2022届高三各地一模试卷专题汇编——立体几何
1.如图1,在边长为4的等边三角形ABC中,D,E,F分别是AB,AC,BC的中点,沿DE把折起,得到如图2所示的四棱锥.
(1)证明:平面.
(2)若二面角的大小为60°,求平面与平面的夹角的大小.
2.如图所示,三棱锥中,平面ABC,若O,Q分别是和的垂心,求证:平面PBC.
3.四面体中,
(1).求证:这个四面体的四个面都是锐角三角形;
(2)有4条长为2的线段和2条长为的线段,用这6条线段作为棱,构成一个三梭锥,问为何值时,可构成一个最大体积的三棱锥,最大值为多少?
(参考公式:三元均值不等式,当且仅当时取得等号)
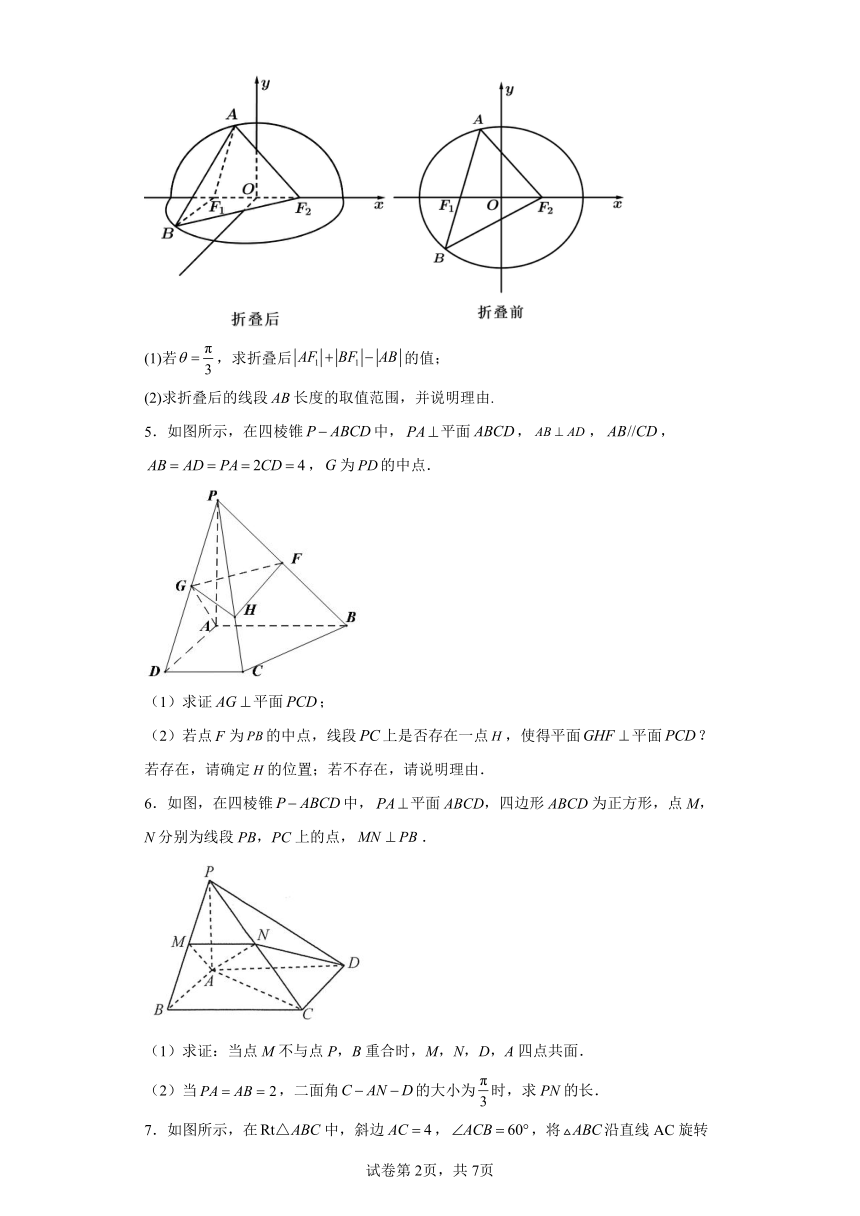
4.已知椭圆:的左 右焦点分别为 ,经过点且倾斜角为 的直线与椭圆交于 两点(其中点在轴上方).将平面沿轴折叠,使轴正半轴和轴所确定的半平面(平面)与轴负半轴和轴所确定的半平面(平面)互相垂直.
(1)若,求折叠后的值;
(2)求折叠后的线段长度的取值范围,并说明理由.
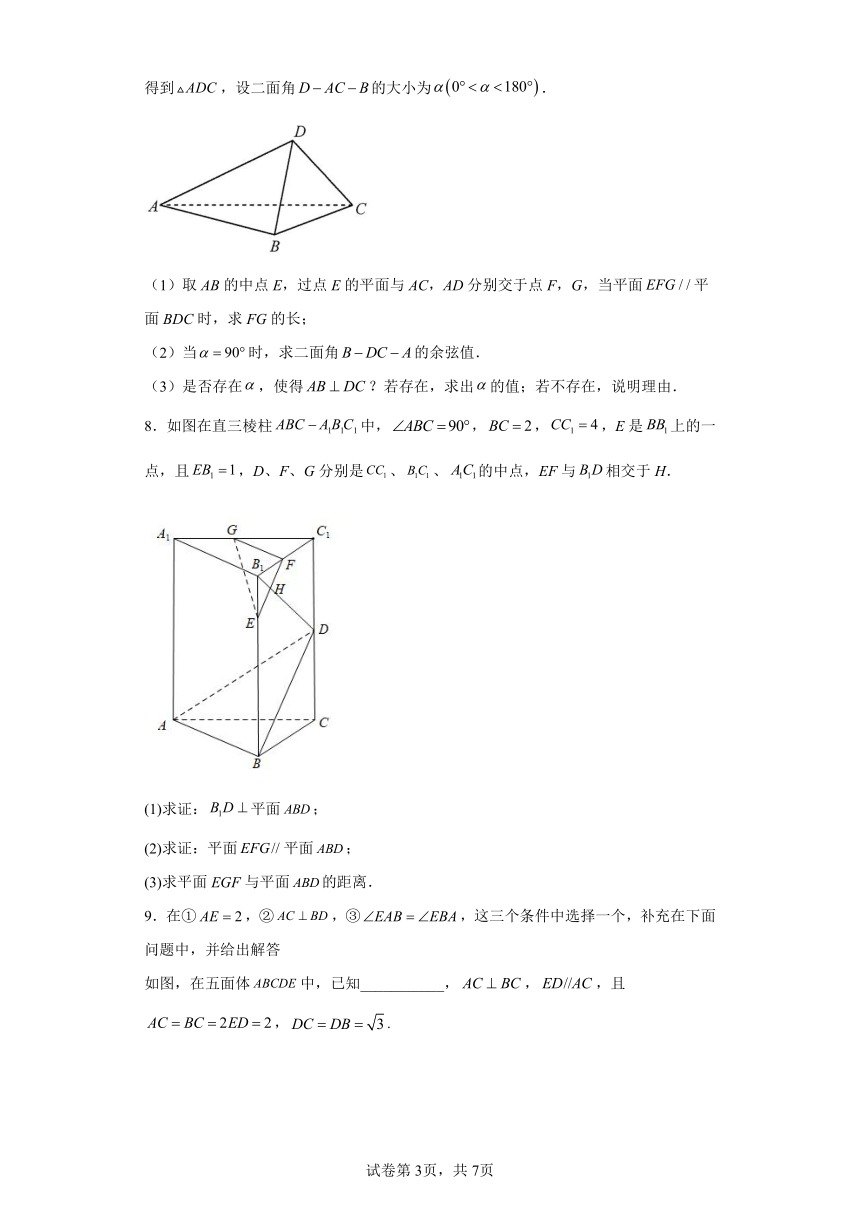
5.如图所示,在四棱锥中,平面,,,,为的中点.
(1)求证平面;
(2)若点为的中点,线段上是否存在一点,使得平面平面?若存在,请确定的位置;若不存在,请说明理由.
6.如图,在四棱锥中,平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC上的点,.
(1)求证:当点M不与点P,B重合时,M,N,D,A四点共面.
(2)当,二面角的大小为时,求PN的长.
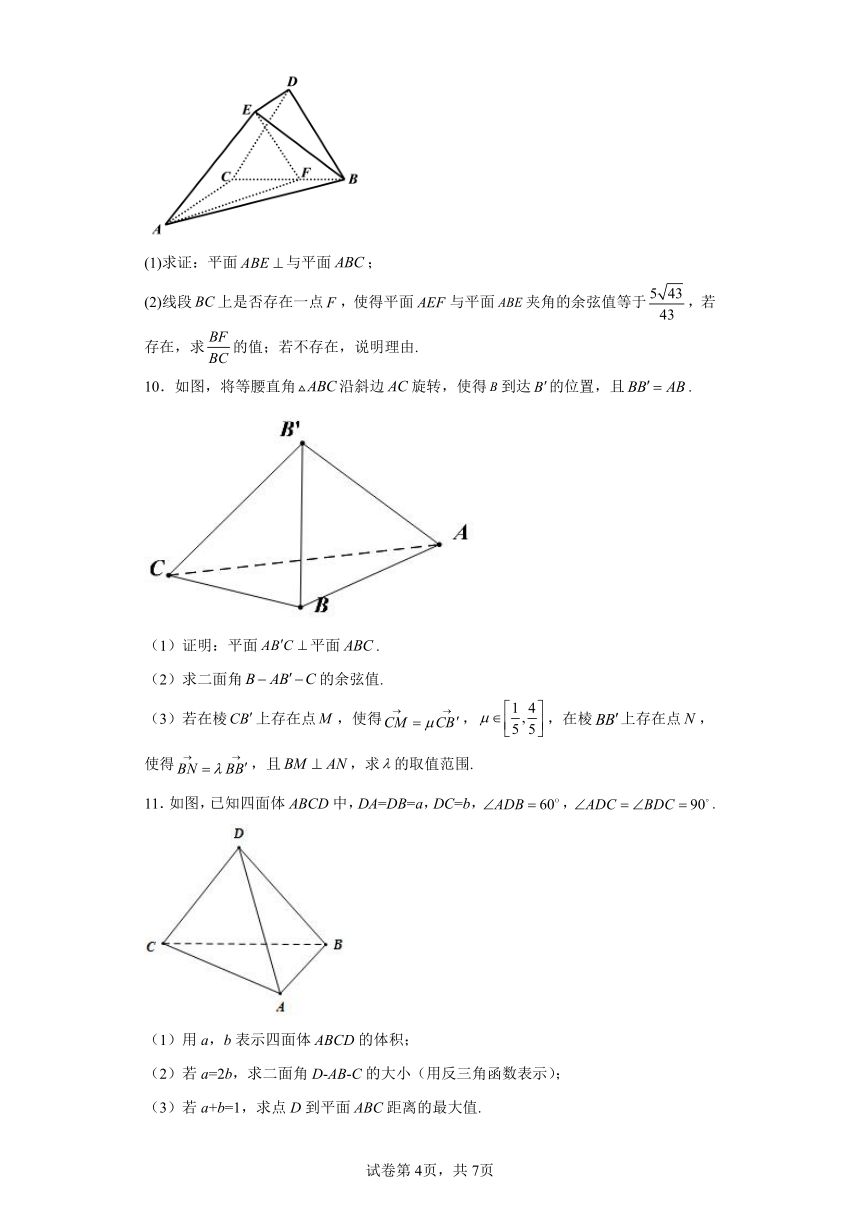
7.如图所示,在中,斜边,,将沿直线AC旋转得到,设二面角的大小为.
(1)取AB的中点E,过点E的平面与AC,AD分别交于点F,G,当平面平面BDC时,求FG的长;
(2)当时,求二面角的余弦值.
(3)是否存在,使得?若存在,求出的值;若不存在,说明理由.
8.如图在直三棱柱中,,,,E是上的一点,且,D、F、G分别是、、的中点,EF与相交于H.
(1)求证:平面;
(2)求证:平面平面;
(3)求平面EGF与平面的距离.
9.在①,②,③,这三个条件中选择一个,补充在下面问题中,并给出解答
如图,在五面体中,已知___________,,,且,.
(1)求证:平面与平面;
(2)线段上是否存在一点,使得平面与平面夹角的余弦值等于,若存在,求的值;若不存在,说明理由.
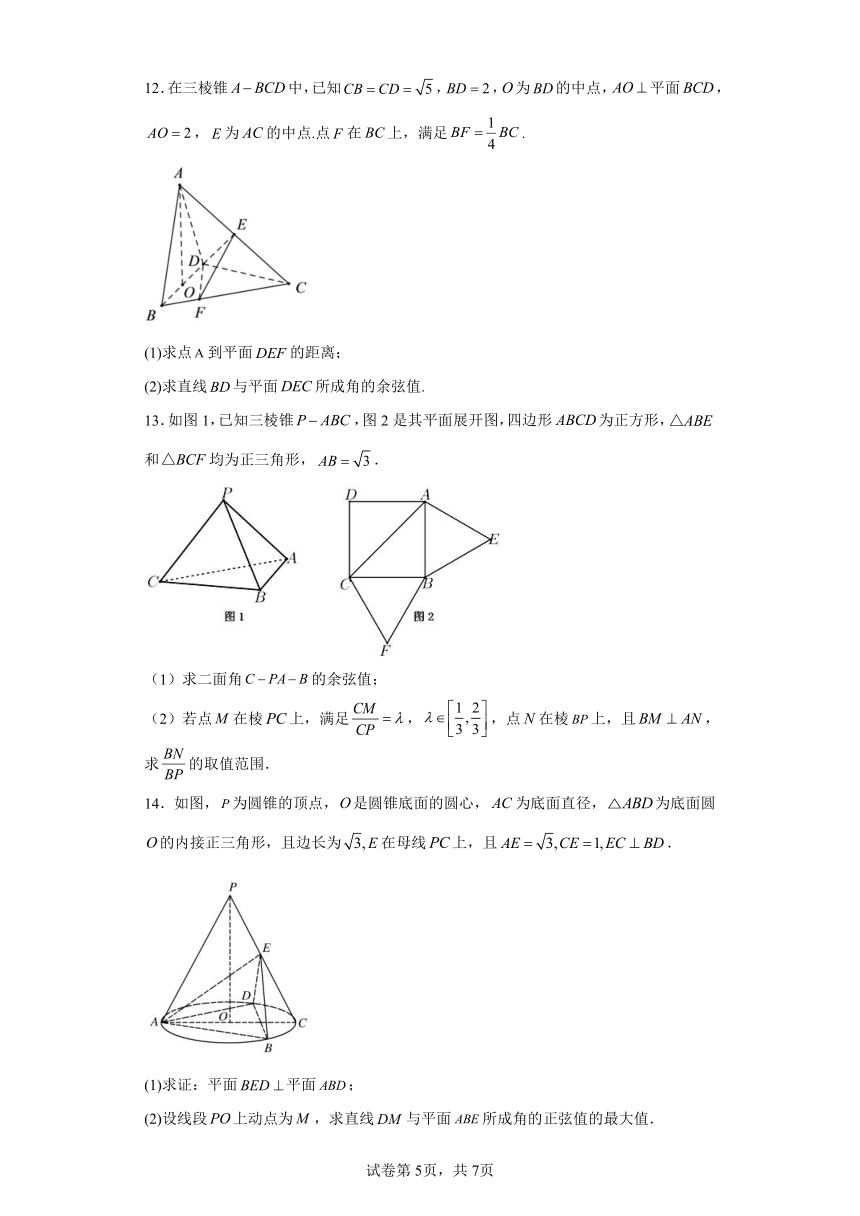
10.如图,将等腰直角沿斜边旋转,使得到达的位置,且.
(1)证明:平面平面.
(2)求二面角的余弦值.
(3)若在棱上存在点,使得,,在棱上存在点,使得,且,求的取值范围.
11.如图,已知四面体ABCD中,DA=DB=a,DC=b,,.
(1)用a,b表示四面体ABCD的体积;
(2)若a=2b,求二面角D-AB-C的大小(用反三角函数表示);
(3)若a+b=1,求点D到平面ABC距离的最大值.
12.在三棱锥中,已知,,为的中点,平面,,为的中点.点在上,满足.
(1)求点到平面的距离;
(2)求直线与平面所成角的余弦值.
13.如图1,已知三棱锥,图2是其平面展开图,四边形为正方形,和均为正三角形,.
(1)求二面角的余弦值;
(2)若点在棱上,满足,,点在棱上,且,求的取值范围.
14.如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,为底面圆的内接正三角形,且边长为在母线上,且.
(1)求证:平面平面;
(2)设线段上动点为,求直线与平面所成角的正弦值的最大值.
15.在四棱锥中,,,,,为正三角形,且平面平面ABCD.
(1)求二面角的余弦值;
(2)线段PB上是否存在一点M(不含端点),使得异面直线DM和PE所成的角的余弦值为?若存在,指出点M的位置;若不存在,请说明理由.
16.如图,在四棱锥中,底面是梯形,,,,.
(1)证明:平面;
(2)若,当四棱锥的体积最大时,求直线与平面所成角的正弦值.
17.如图,四棱锥的底面是平行四边形,,,,,,点是线段(包括端点)上的动点.
(1)若()时,平面平面,求的值;
(2)平面和平面的夹角为,直线与平面所成角为,求的值.
18.在长方体中,求证:.
19.在直三棱柱中,D,E,F分别为A1C1,AB1,BB1的中点.
(1)证明∶DE//平面B1BCC1;
(2)若AB=AC=AA1=2,AF⊥DE,求直三棱柱外接球的表面积.
20.如图所示,三棱柱ABC﹣A1B1C1中,侧面BB1C1C是边长为2的正方形,ACC1A1是菱形,,且平面BB1C1C垂直平面ACC1A1,M为A1C1中点.
(1)求证:平面MBC⊥平面A1B1C1;
(2)求点C1到平面MB1C的距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)证明见解析;
(2).
【解析】
【分析】
(1)由结合线面平行的判定即可推理作答.
(2)取DE的中点M,连接,FM,证明平面平面,再建立空间直角坐标系,借助空间向量推理、计算作答.
(1)
在中,因为E,F分别是AC,BC的中点,所以,
则在图2中,,而平面,平面,
所以平面.
(2)
依题意,是正三角形,四边形是菱形,取DE的中点M,连接,FM,如图,
则,,即是二面角的平面角,,
取中点N,连接,则有,在中,由余弦定理得:
,
于是有,,即,
而,,,平面,则平面,
又平面,从而有平面平面,因平面平面,平面,
因此,平面,过点N作,则两两垂直,
以点N为原点,射线分别为x,y,z轴非负半轴建立空间直角坐标系,
则,,,,
,,,
设平面的法向量,则,令,得,
设平面的法向量,则,令,得,
显然有,即,
所以平面与平面的夹角为.
【点睛】
方法点睛:利用向量法求二面角:(1)找法向量,分别求出两个半平面所在平面的法向量,然后求得法向量的夹角,结合图形得到二面角的大小;
(2)找与交线垂直的直线的方向向量,分别在二面角的两个半平面内找到与交线垂直且以垂足为起点的直线的方向向量,则这两个向量的夹角就是二面角的平面角.
2.证明见解析
【解析】
【分析】
先证明平面,进而证明出,同理证明出,从而证明出平面PBC.
【详解】
证明:如图,连接AO并延长交BC于点E,连接PE.
∵平面ABC,BC平面ABC,∴,
∵(由于O是的垂心),,∴平面
∵平面,∴
因为为的垂心,∴点Q在PE上.
∵平面,平面,∴①
连接BO并延长交AC于点F,则.
连接BQ并延长交PC于点M,则.连接MF.
∵平面ABC,平面ABC,∴
∵,,∴平面
∵平面,∴.
∴而,∴平面,而平面,∴②
∵,由①②知:平面PBC.
3.(1)证明见解析;(2)当时,三棱锥体积最大为.
【解析】
【分析】
(1)在四面体中,由已知可得四面体的四个面为全等三角形,设长方体的长、宽、高分别为、、,证明为锐角三角形,即可证明这个四面体的四个面都是锐角三角形;
(2)当2条长为的线段不在同一个三角形中,写出三棱锥体积,利用基本不等式求最值;当边长为的两条棱在同一个三角形中时,可知当平面时,体积取最大值,比较大小的结论.
【详解】
(1)∵四面体,如图,
故四面体中四个面为全等三角形,
即只需证明一个为锐角三角形即可,设长方体长宽高分别为,则,
∴,∴为锐角三角形,故四面体四个面都为锐角三角形;
(2)解:2条长为的线段不在同一个三角形中,此时长为的两条线段必还在三棱锥的对棱,不妨设,
取中点,连接,(如图),
则,,则平面,,
在中,,,
,
∴,
由均值不等式,等号当且仅当时成立,即,
∴此时,
当边长为的两条棱在同一个三角形中时,设,
当且仅当平面时,体积取最大,此时,
∵,
综上,当时,三棱锥体积最大为
4.(1);
(2),理由见解析.
【解析】
【分析】
(1)设折叠之前,,直线的方程为:与椭圆方程联立可得,,如图建立空间直角坐标系,求出三点坐标,结合椭圆的焦半径公式以及两点间距离,可将表示成关于,的代数式,由可得,的值即可求解;
(2)结合(1)可将表示成关于的函数,,再利用换元法结合二次函数的单调性即可求解.
(1)
由可得,,所以,点,
在没有折叠之前,设直线的方程为:,,,
记折叠后点为坐标原点,原轴正半轴为折叠后空间直角坐标系中轴正方向,原轴正半轴为折叠后空间直角坐标系中轴正方向,原轴负半轴为折叠后空间直角坐标系中轴正方向,可得,,,
椭圆的左准线方程为:,
所以,,
则
①,
由可得,
所以,,
当时,,可得,,
代入①得:
.
(2)
因为,所以,
由(1)知:
,
令,
可得,
因为,在上单调递减,
所以的范围为,
所以
所以折叠后的线段长度的取值范围为.
【点睛】
解决圆锥曲线中的范围或最值问题时,若题目的条件和结论能体现出明确的函数关系,则可先建立目标函数,再求这个函数的最值.在利用代数法解决最值与范围问题时常从以下几个方面考虑:
①利用判别式构造不等关系,从而确定参数的取值范围;
②利用已知参数的范围,求出新参数的范围,解题的关键是建立两个参数之间的等量关系;
③利用基本不等式求出参数的取值范围;
④利用函数值域的求法,确定参数的取值范围.
5.(1)证明见解析;(2)存在;.
【解析】
【分析】
(1)先证明平面,进而得到面,得出,再根据条件证明,最后根据线面垂直的判定定理得到结论;
(2)建立空间直角坐标系,设,求出两个平面的法向量,进而根据面面垂直求出k.
【详解】
(1)因为平面,所以,又,,所以平面,又,所以面,面,.
又,为的中点,所以,而,所以平面.
(2)以A为坐标原点,所在方向分别为x,y,z轴正方向建立空间直角坐标系,如图,则,,,,,,.
所以,设(),所以,则,所以,,
设平面的法向量为,则,,
即,令,则,
由(1)可知为平面的一个法向量,若平面平面,则,即,解得.
即时平面平面.
6.(1)详见解析;(2).
【解析】
【分析】
(1)易证平面PAB,得到,,平面PBC,平面PBC,得到,再结合四边形ABCD为正方形,利用平面的基本性质证明;
(2)以A为原点,分别以AB,AD,AP为x,y,z轴建立空间直角坐标系,设平面AND的一个法向量为,平面ANC的一个法向量为,,根据二面角的大小为,由求解.
【详解】
(1)因为平面ABCD,
所以,又因为,
所以平面PAB,
所以,
又因为,平面PBC,平面PBC,
所以,
又因为四边形ABCD为正方形,
所以,
所以,
所以当点M不与点P,B重合时,M,N,D,A四点共面.
(2)以A为原点,分别以AB,AD,AP为x,y,z轴建立空间直角坐标系,如图所示:
则,
设平面AND的一个法向量为,
设平面ANC的一个法向量为,
设,
因为,则,
又,
则,即,
令,得,
又,
则,即,
令,得,
因为二面角的大小为,
所以,
解得,
因为,
所以.
7.(1)1;(2);(3)不存在.
【解析】
【分析】
(1)根据平面平面BDC,得到,再由E为AB的中点,得到G,F都为相应边的中点,从而由求解;
(2)过点B作,连接DO,则,由,易证平面ABC,以O为原点,建立空间直角坐标系,求得平面BCD的一个法向量,易知是平面ACD的一个法向量,再由求解;
(3)假设存在,由求解.
【详解】
(1)如图所示:
因为平面平面BDC,平面平面BDC=BD,平面平面EFG=EG,
所以,
因为E为AB的中点,所以G为AD的中点,
同理可证F为AC的中点,
所以,
在中,斜边,,
所以,即,
所以;
(2)过点B作,连接DO,则,面,
因为,则平面平面ABC,因为平面平面ABC=AC,
所以平面ABC,
以O为原点,建立如图所示空间直角坐标系;
在中,斜边,,
所以,
则,
所以 ,
设平面BCD的一个法向量为,
则,即,
令 ,得 ,则,
因为平面ACD,
所以是平面ACD的一个法向量,
所以.
即二面角的余弦值是.
(3)假设存在,则,
,
,
解得,则,
因为,
所以不存在,使得.
8.(1)证明见解析;
(2)证明见解析;
(3).
【解析】
【分析】
(1)根据面面垂直的性质定理可得,进而推出,再结合的边长,利用勾股定理即可推出,最后结合线面垂直的判定定理即可完成证明;
(2)根据是的中位线,即可证明,再利用,即可证明,再根据题意条件,证明,最后利用面面平行的判定定理即可完成证明;
(3)由(2)可知,平面平面,而,因此平面EGF与平面的距离就是两条平行线之间的距离,再结合四边形的边角关系,可得是的公垂线,即为两个平面之间的距离,求出即可完成距离的求解.
(1)
在直三棱柱中, ,交线为,而,,,,
根据已知条件可得,为的中点,,,结合勾股定理可得,,所以平面.
(2)
如图所示,取的中点,连接,,,为的中点,而为的中点,为的中位线,,又,且,,,,,
F、G分别是、的中点,是的中位线,,
在直三棱柱中,,,,,又,平面平面.
(3)
由平面平面,EF与相交于H,又 平面,平面,两平面之间的距离即为H到平面的距离,即, ,
∽,,,
故平面EGF与平面的距离为.
9.(1)证明见解析;
(2)存在;.
【解析】
【分析】
(1)若选①,取中点,中点,中点,可证得四边形为平行四边形,从而利用勾股定理和平行关系证得,由线面垂直和面面垂直判定得到平面平面,利用面面垂直性质可证得平面;
若选②,取中点,中点,由线面垂直和面面垂直的判定可证得平面平面,利用面面垂直性质可证得平面;
若选③,取中点,中点,根据长度和平行关系可证得四边形为平行四边形,由此确定,得到,结合可得,从而利用勾股定理和平行关系证得,由线面垂直和面面垂直判定得到平面平面,利用面面垂直性质可证得平面;
三个条件均可说明两两互相垂直,则以为坐标原点可建立空间直角坐标系,利用面面垂直的向量证明方法可证得结论;
(2)假设存在满足题意的点,利用二面角的向量求法可构造方程求得,由此可确定点位置,得到的值.
(1)
若选①,取中点,中点,中点,连接,
,,四边形为平行四边形,,
,又,,,,
又,,又,,平面,
平面,平面,平面平面,
,,又平面,平面平面,
平面,又,,;
若选②,,,,平面,
平面,平面,平面平面,
取中点,中点,连接,
,,又平面,平面平面,
平面,又,,;
若选③,取中点,中点,连接,
,,又,;
分别为中点,,又,,
四边形为平行四边形,;
,,,,,
,,,
,又,,
又,,平面,
平面,平面,平面平面,
又,平面,平面平面,
平面,又,,;
综上所述:两两互相垂直,
则以为坐标原点,为轴,可建立如图所示空间直角坐标系,
则,,,,,
平面,平面的一个法向量;
设平面的法向量,
则,令,解得:,,,
,即,平面与平面.
(2)
设在线段上存在点,使得平面与平面夹角的余弦值等于,
由(1)得:,,
设平面的法向量,
则,令,则,,
;
,
化简可得:,解得:或(舍),
,,;
综上所述:在线段上存在点,满足,使得平面与平面夹角的余弦值等于.
10.(1)证明见解析;(2);(3).
【解析】
【分析】
(1)取的中点为,进而证明平面,然后根据面面垂直的判定定理得到答案;
(2)建立空间直角坐标系,进而根据空间向量的夹角公式求得答案;
(3)根据空间向量的坐标运算得出与间的关系式,进而求出的取值范围.
【详解】
(1)取的中点为,连接,.
由题意得,,
在中,因为为的中点,所以,即.
易得与全等,则,即.
因为,所以平面.
因为平面,所以平面平面.
(2)不妨设,由(1)平面,易知OB⊥AC,
如图,以为坐标原点,分别以,,所在直线为轴,轴,轴,建立空间直角坐标系,则,,,,,,,
设平面的法向量为,则得
不妨取,则.
因为,所以平面,所以平面的一个法向量为.
因为.
又二面角是锐二面角,所以二面角的余弦值为.
(3)结合(2)可得,,.
,
.
因为,所以,得.
即,是关于的单调递增函数,
当时,,故的取值范围是.
11.(1);(2);(3)
【解析】
【分析】
(1)由棱锥的体积计算即可;(2)取的中点,连接,可证明为二面角D-AB-C 的平面角,求出相关量可计算结果;(3)等体积法计算点到平面的距离,三元基本不等式求最值,求出距离的最大值.
【详解】
解:(1)该四面体可看作以为底面,以为高的三棱锥,DA=DB=a,
,所以为等边三角形,,
所以.
(2)取的中点,连接 则,因为,且DA=DB,所以,则,所以,则为二面角D-AB-C 的平面角.
因为,即,,,所以平面,即,又,,所以,所以,即二面角D-AB-C的大小为.
.
(3)三棱锥可看作以为底面,以为高的三棱锥,也可看作以为底面,为顶点的三棱锥,设到底面的距离为,则有.
由(2)可知,为等腰三角形,,则;即 ,解得:,令
当且仅当时等号成立,
所以
12.(1)
(2)
【解析】
【分析】
(1)求平面一个法向量,利用空间向量求点到线的距离公式求解;
(2)求平面得一个法向量,利用空间向量求线面角即可得解.
(1)
连接,∵,,∴,又平面,
以为原点,,,为,,轴建立空间直角坐标系,
则,,,,
由为的中点,知,
设,又,知,
则设平面一个法向量为,,
, 令,∴
所以点到平面的距离为
(2)
设平面一个法向量为,,
,令,∴
又,设直线与平面所成角为
,.
所以直线与平面所成角的余弦值为
13.(1);(2).
【解析】
【分析】
(1)取的中点,的中点,连接,,,可证明为二面角的平面角,根据长度关系,即得解;
(2)过点作交于点,在中,由余弦定理可得,设,由三角形相似可得,,在中,由余弦定理可得,
在、分别使用勾股定理,联立可得,结合,即得解.
【详解】
(1)取的中点,的中点,连接,,,
在中,,,则,
在等边中,,
故为二面角的平面角,
因为,所以,,,
则,所以,
则,故二面角的余弦值为;
(2)过点作交于点,
因为,则,又,所以,
在中,,
所以,设,则,
所以,,
在中,,
所以,因为,
则,
在中,①,
在中,②,
由①=②,可得,因为,所以,
故的取值范围为.
14.(1)证明见解析
(2)1
【解析】
【分析】
(1)设交于点连接,由,
并结合可证得平面由此证得,
再利用三角形相似证得从而证得平面进而证得平面平面;
(2)建立空间直角坐标系,设,
通过向量和平面的法向量建立直线与平面所成角的正弦值的关系式,并利用基本不等式,即可求最值.
(1)
证明:如图,设交于点连接,
易知,
又平面平面,
又平面.又是底面圆的内接正三角形,
由,可得,.又,,
即.又,,
,即.又平面,,
平面.又平面,平面平面.
(2)
易知.以点为坐标原点,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,
则,
设平面的法向量为,
则,即,令,则.设,
可得.
设直线与平面所成的角为,则.
令,,则
,当且仅当时,等号成立,
当时,有最大值,
于是当时,有最大值为,
的最大值为,
故直线与平面所成角的正弦值的最大值为.
15.(1)
(2)存在,点M位置为
【解析】
【分析】
(1)建立空间直角坐标系,利用向量法求二面角的余弦值;
(2)设,利用向量法求异面直线的夹角,得到,解方程即得解.
(1)
设是中点,为正三角形,则.
因为平面平面ABCD,平面平面,
又平面PAD,所以面ABCD.
又因为,,
所以为正三角形,所以,
以为原点,分别以为轴的正方向,建立空间直角坐标系,
则,,,,
于是,,.
设平面PEC的法向量为,
由即可取.
平面EBC的一个法向量为,
设二面角的平面角为,则
由图知为为钝角,所以二面角的余弦值为.
(2)
设,则,
,,
所以,
解得或0(舍),所以存在点M使得.
16.(1)证明见解析;(2).
【解析】
【分析】
(1)取,中点,,连接,,,得到面面,故可先将要证平面转化为求证面即可求证;
(2)可以通过建立空间直角坐标系,利用空间向量进行求解.
【详解】
(1)取,中点,,连接,,.
由,得,,
又,
所以平面.
由,知四边形是平行四边形,则,
平面,平面,所以平面,
同理平面,且,
所以平面平面,
所以平面.
(2)由,
知四边形是以的等腰梯形.
连接,则,
又平面,所以,
所以平面,又平面,
所以平面平面,
于是点在底面内的射影在上.
(在平面中,,点在以AC为直径的圆上运动)
取中点,则,
于是当底面时,四棱锥的体积最大.
如图,以为原点,分别以射线,,为,,轴的正半轴,
建立空间直角坐标系.
由题意得,,,
,.
所以,,.
设平面的法向量,
由,得,
取,则.
因此,直线与平面所成角的正弦值为.
17.(1)或
(2)
【解析】
【分析】
(1)建立空间直角坐标系,利用向量法列方程,化简求得的值.
(2)求得,,结合三角恒等变换求得,进而求得.
(1)
由于,所以,
在三角形中,由余弦定理得,
所以,所以,
依题意可知,
由于,所以平面,所以,.
以为空间坐标原点建立如图所示空间直角坐标系,
,
①当时:
,,
,
设平面的法向量为,
则,
故可设,
设平面的法向量为,
则
故可设,
由于平面平面,
所以,解得.
②当时,点与点重合,
平面(即平面)的法向量为,
设平面(即平面)的法向量为,
则,
故可设,
,即平面平面不成立,也即平面平面不成立.
③当时,点与点重合,
平面即平面,设平面即平面,
由于,所以平面.
由于平面,所以平面平面,也即平面平面成立.
综上所述,的为或.
(2)
①当时:
由(1)可知,平面的法向量为,
平面的法向量为,
所以.
,
所以.
,由于,所以.
②当时,点与点重合,,,
设平面的法向量为,
则,
故可设.
,.
,由于,所以.
综上所述,.
18.证明见解析.
【解析】
【分析】
利用长方体的特性可得,再利用三角恒等变换并结合三角函数性质即可得解.
【详解】
画出长方体,如图,
设,,,则、、均为锐角,
显然,则,
于是得,
而,则,即,同理,,因此,,
从而有,因,,
于是得,因此,,
综上得:,
所以.
19.(1)证明见解析;(2).
【解析】
【分析】
(1)作辅助线,利用线线平行或者面面平行,皆可证明线面平行.
(2) 先由AF⊥DE求出再根据直棱柱外接球半径的求法,即可求解.
【详解】
(1)证明∶取B1C1的中点G,连接DG,EF,FG,如图1,
则DG//A1B1,且;EF//AB,且,
又AB//A1B1,AB=A1B1,所以EF//DG,且EF= DG,
所以DEFG为平行四边形,所以DE//GF.
又平面 平面,
所以DE//平面
(注∶本题也可以取A1B1的中点H,连接DH,HE,利用平面DEH//平面B1BCC1来证DE//平面B1BCC1,如图2)
(2)解∶设,由已知,得,且,
则,
因为AF⊥DE,
所以,
解得,即
又AB=AC,则△ABC为等边三角形,
直三棱柱外接球的球心为△ABC与△A1B1C1中心连线O1O2的中点O,如图3,连接为直三棱柱ABC-A1B1C1外接球的半径.
因为,,所以,
所以直三棱柱外接球的表面积为
20.(1)证明见解析;(2).
【解析】
【分析】
(1)利用平面BB1C1C平面ACC1A1,,得到平面,又平面,得,由题意得,即可证明;
(2)利用等体积法,即可求解.
【详解】
(1)证明:∵正方形BB1C1C,,
∵面⊥面,面面,面,
∴B1C1⊥面ACC1A1,
又CM 面ACC1A1,∴B1C1⊥CM,
∵ACC1A1是菱形,,
∴为等边三角形,
∵M为A1C1中点,∴CM⊥A1C1,
又A1C1∩B1C1=C1,且A1C1,B1C1 面A1B1C1,
∴CM⊥面A1B1C1,
又CM 面MBC,
∴平面MBC⊥平面A1B1C1.
(2)解:由(1)可知,B1C1⊥面ACC1A1,
∴B1到平面MCC1的距离为B1C1=2,
由(1)知,CM⊥面A1B1C1,
∵MB1 面A1B1C1,∴CM⊥MB1,
在中,,
在中,,
,,
设点C1到平面MB1C的距离为h,
,
,
,
故点C1到平面MB1C的距离为.
答案第1页,共2页
答案第1页,共2页
1.如图1,在边长为4的等边三角形ABC中,D,E,F分别是AB,AC,BC的中点,沿DE把折起,得到如图2所示的四棱锥.
(1)证明:平面.
(2)若二面角的大小为60°,求平面与平面的夹角的大小.
2.如图所示,三棱锥中,平面ABC,若O,Q分别是和的垂心,求证:平面PBC.
3.四面体中,
(1).求证:这个四面体的四个面都是锐角三角形;
(2)有4条长为2的线段和2条长为的线段,用这6条线段作为棱,构成一个三梭锥,问为何值时,可构成一个最大体积的三棱锥,最大值为多少?
(参考公式:三元均值不等式,当且仅当时取得等号)
4.已知椭圆:的左 右焦点分别为 ,经过点且倾斜角为 的直线与椭圆交于 两点(其中点在轴上方).将平面沿轴折叠,使轴正半轴和轴所确定的半平面(平面)与轴负半轴和轴所确定的半平面(平面)互相垂直.
(1)若,求折叠后的值;
(2)求折叠后的线段长度的取值范围,并说明理由.
5.如图所示,在四棱锥中,平面,,,,为的中点.
(1)求证平面;
(2)若点为的中点,线段上是否存在一点,使得平面平面?若存在,请确定的位置;若不存在,请说明理由.
6.如图,在四棱锥中,平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC上的点,.
(1)求证:当点M不与点P,B重合时,M,N,D,A四点共面.
(2)当,二面角的大小为时,求PN的长.
7.如图所示,在中,斜边,,将沿直线AC旋转得到,设二面角的大小为.
(1)取AB的中点E,过点E的平面与AC,AD分别交于点F,G,当平面平面BDC时,求FG的长;
(2)当时,求二面角的余弦值.
(3)是否存在,使得?若存在,求出的值;若不存在,说明理由.
8.如图在直三棱柱中,,,,E是上的一点,且,D、F、G分别是、、的中点,EF与相交于H.
(1)求证:平面;
(2)求证:平面平面;
(3)求平面EGF与平面的距离.
9.在①,②,③,这三个条件中选择一个,补充在下面问题中,并给出解答
如图,在五面体中,已知___________,,,且,.
(1)求证:平面与平面;
(2)线段上是否存在一点,使得平面与平面夹角的余弦值等于,若存在,求的值;若不存在,说明理由.
10.如图,将等腰直角沿斜边旋转,使得到达的位置,且.
(1)证明:平面平面.
(2)求二面角的余弦值.
(3)若在棱上存在点,使得,,在棱上存在点,使得,且,求的取值范围.
11.如图,已知四面体ABCD中,DA=DB=a,DC=b,,.
(1)用a,b表示四面体ABCD的体积;
(2)若a=2b,求二面角D-AB-C的大小(用反三角函数表示);
(3)若a+b=1,求点D到平面ABC距离的最大值.
12.在三棱锥中,已知,,为的中点,平面,,为的中点.点在上,满足.
(1)求点到平面的距离;
(2)求直线与平面所成角的余弦值.
13.如图1,已知三棱锥,图2是其平面展开图,四边形为正方形,和均为正三角形,.
(1)求二面角的余弦值;
(2)若点在棱上,满足,,点在棱上,且,求的取值范围.
14.如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,为底面圆的内接正三角形,且边长为在母线上,且.
(1)求证:平面平面;
(2)设线段上动点为,求直线与平面所成角的正弦值的最大值.
15.在四棱锥中,,,,,为正三角形,且平面平面ABCD.
(1)求二面角的余弦值;
(2)线段PB上是否存在一点M(不含端点),使得异面直线DM和PE所成的角的余弦值为?若存在,指出点M的位置;若不存在,请说明理由.
16.如图,在四棱锥中,底面是梯形,,,,.
(1)证明:平面;
(2)若,当四棱锥的体积最大时,求直线与平面所成角的正弦值.
17.如图,四棱锥的底面是平行四边形,,,,,,点是线段(包括端点)上的动点.
(1)若()时,平面平面,求的值;
(2)平面和平面的夹角为,直线与平面所成角为,求的值.
18.在长方体中,求证:.
19.在直三棱柱中,D,E,F分别为A1C1,AB1,BB1的中点.
(1)证明∶DE//平面B1BCC1;
(2)若AB=AC=AA1=2,AF⊥DE,求直三棱柱外接球的表面积.
20.如图所示,三棱柱ABC﹣A1B1C1中,侧面BB1C1C是边长为2的正方形,ACC1A1是菱形,,且平面BB1C1C垂直平面ACC1A1,M为A1C1中点.
(1)求证:平面MBC⊥平面A1B1C1;
(2)求点C1到平面MB1C的距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)证明见解析;
(2).
【解析】
【分析】
(1)由结合线面平行的判定即可推理作答.
(2)取DE的中点M,连接,FM,证明平面平面,再建立空间直角坐标系,借助空间向量推理、计算作答.
(1)
在中,因为E,F分别是AC,BC的中点,所以,
则在图2中,,而平面,平面,
所以平面.
(2)
依题意,是正三角形,四边形是菱形,取DE的中点M,连接,FM,如图,
则,,即是二面角的平面角,,
取中点N,连接,则有,在中,由余弦定理得:
,
于是有,,即,
而,,,平面,则平面,
又平面,从而有平面平面,因平面平面,平面,
因此,平面,过点N作,则两两垂直,
以点N为原点,射线分别为x,y,z轴非负半轴建立空间直角坐标系,
则,,,,
,,,
设平面的法向量,则,令,得,
设平面的法向量,则,令,得,
显然有,即,
所以平面与平面的夹角为.
【点睛】
方法点睛:利用向量法求二面角:(1)找法向量,分别求出两个半平面所在平面的法向量,然后求得法向量的夹角,结合图形得到二面角的大小;
(2)找与交线垂直的直线的方向向量,分别在二面角的两个半平面内找到与交线垂直且以垂足为起点的直线的方向向量,则这两个向量的夹角就是二面角的平面角.
2.证明见解析
【解析】
【分析】
先证明平面,进而证明出,同理证明出,从而证明出平面PBC.
【详解】
证明:如图,连接AO并延长交BC于点E,连接PE.
∵平面ABC,BC平面ABC,∴,
∵(由于O是的垂心),,∴平面
∵平面,∴
因为为的垂心,∴点Q在PE上.
∵平面,平面,∴①
连接BO并延长交AC于点F,则.
连接BQ并延长交PC于点M,则.连接MF.
∵平面ABC,平面ABC,∴
∵,,∴平面
∵平面,∴.
∴而,∴平面,而平面,∴②
∵,由①②知:平面PBC.
3.(1)证明见解析;(2)当时,三棱锥体积最大为.
【解析】
【分析】
(1)在四面体中,由已知可得四面体的四个面为全等三角形,设长方体的长、宽、高分别为、、,证明为锐角三角形,即可证明这个四面体的四个面都是锐角三角形;
(2)当2条长为的线段不在同一个三角形中,写出三棱锥体积,利用基本不等式求最值;当边长为的两条棱在同一个三角形中时,可知当平面时,体积取最大值,比较大小的结论.
【详解】
(1)∵四面体,如图,
故四面体中四个面为全等三角形,
即只需证明一个为锐角三角形即可,设长方体长宽高分别为,则,
∴,∴为锐角三角形,故四面体四个面都为锐角三角形;
(2)解:2条长为的线段不在同一个三角形中,此时长为的两条线段必还在三棱锥的对棱,不妨设,
取中点,连接,(如图),
则,,则平面,,
在中,,,
,
∴,
由均值不等式,等号当且仅当时成立,即,
∴此时,
当边长为的两条棱在同一个三角形中时,设,
当且仅当平面时,体积取最大,此时,
∵,
综上,当时,三棱锥体积最大为
4.(1);
(2),理由见解析.
【解析】
【分析】
(1)设折叠之前,,直线的方程为:与椭圆方程联立可得,,如图建立空间直角坐标系,求出三点坐标,结合椭圆的焦半径公式以及两点间距离,可将表示成关于,的代数式,由可得,的值即可求解;
(2)结合(1)可将表示成关于的函数,,再利用换元法结合二次函数的单调性即可求解.
(1)
由可得,,所以,点,
在没有折叠之前,设直线的方程为:,,,
记折叠后点为坐标原点,原轴正半轴为折叠后空间直角坐标系中轴正方向,原轴正半轴为折叠后空间直角坐标系中轴正方向,原轴负半轴为折叠后空间直角坐标系中轴正方向,可得,,,
椭圆的左准线方程为:,
所以,,
则
①,
由可得,
所以,,
当时,,可得,,
代入①得:
.
(2)
因为,所以,
由(1)知:
,
令,
可得,
因为,在上单调递减,
所以的范围为,
所以
所以折叠后的线段长度的取值范围为.
【点睛】
解决圆锥曲线中的范围或最值问题时,若题目的条件和结论能体现出明确的函数关系,则可先建立目标函数,再求这个函数的最值.在利用代数法解决最值与范围问题时常从以下几个方面考虑:
①利用判别式构造不等关系,从而确定参数的取值范围;
②利用已知参数的范围,求出新参数的范围,解题的关键是建立两个参数之间的等量关系;
③利用基本不等式求出参数的取值范围;
④利用函数值域的求法,确定参数的取值范围.
5.(1)证明见解析;(2)存在;.
【解析】
【分析】
(1)先证明平面,进而得到面,得出,再根据条件证明,最后根据线面垂直的判定定理得到结论;
(2)建立空间直角坐标系,设,求出两个平面的法向量,进而根据面面垂直求出k.
【详解】
(1)因为平面,所以,又,,所以平面,又,所以面,面,.
又,为的中点,所以,而,所以平面.
(2)以A为坐标原点,所在方向分别为x,y,z轴正方向建立空间直角坐标系,如图,则,,,,,,.
所以,设(),所以,则,所以,,
设平面的法向量为,则,,
即,令,则,
由(1)可知为平面的一个法向量,若平面平面,则,即,解得.
即时平面平面.
6.(1)详见解析;(2).
【解析】
【分析】
(1)易证平面PAB,得到,,平面PBC,平面PBC,得到,再结合四边形ABCD为正方形,利用平面的基本性质证明;
(2)以A为原点,分别以AB,AD,AP为x,y,z轴建立空间直角坐标系,设平面AND的一个法向量为,平面ANC的一个法向量为,,根据二面角的大小为,由求解.
【详解】
(1)因为平面ABCD,
所以,又因为,
所以平面PAB,
所以,
又因为,平面PBC,平面PBC,
所以,
又因为四边形ABCD为正方形,
所以,
所以,
所以当点M不与点P,B重合时,M,N,D,A四点共面.
(2)以A为原点,分别以AB,AD,AP为x,y,z轴建立空间直角坐标系,如图所示:
则,
设平面AND的一个法向量为,
设平面ANC的一个法向量为,
设,
因为,则,
又,
则,即,
令,得,
又,
则,即,
令,得,
因为二面角的大小为,
所以,
解得,
因为,
所以.
7.(1)1;(2);(3)不存在.
【解析】
【分析】
(1)根据平面平面BDC,得到,再由E为AB的中点,得到G,F都为相应边的中点,从而由求解;
(2)过点B作,连接DO,则,由,易证平面ABC,以O为原点,建立空间直角坐标系,求得平面BCD的一个法向量,易知是平面ACD的一个法向量,再由求解;
(3)假设存在,由求解.
【详解】
(1)如图所示:
因为平面平面BDC,平面平面BDC=BD,平面平面EFG=EG,
所以,
因为E为AB的中点,所以G为AD的中点,
同理可证F为AC的中点,
所以,
在中,斜边,,
所以,即,
所以;
(2)过点B作,连接DO,则,面,
因为,则平面平面ABC,因为平面平面ABC=AC,
所以平面ABC,
以O为原点,建立如图所示空间直角坐标系;
在中,斜边,,
所以,
则,
所以 ,
设平面BCD的一个法向量为,
则,即,
令 ,得 ,则,
因为平面ACD,
所以是平面ACD的一个法向量,
所以.
即二面角的余弦值是.
(3)假设存在,则,
,
,
解得,则,
因为,
所以不存在,使得.
8.(1)证明见解析;
(2)证明见解析;
(3).
【解析】
【分析】
(1)根据面面垂直的性质定理可得,进而推出,再结合的边长,利用勾股定理即可推出,最后结合线面垂直的判定定理即可完成证明;
(2)根据是的中位线,即可证明,再利用,即可证明,再根据题意条件,证明,最后利用面面平行的判定定理即可完成证明;
(3)由(2)可知,平面平面,而,因此平面EGF与平面的距离就是两条平行线之间的距离,再结合四边形的边角关系,可得是的公垂线,即为两个平面之间的距离,求出即可完成距离的求解.
(1)
在直三棱柱中, ,交线为,而,,,,
根据已知条件可得,为的中点,,,结合勾股定理可得,,所以平面.
(2)
如图所示,取的中点,连接,,,为的中点,而为的中点,为的中位线,,又,且,,,,,
F、G分别是、的中点,是的中位线,,
在直三棱柱中,,,,,又,平面平面.
(3)
由平面平面,EF与相交于H,又 平面,平面,两平面之间的距离即为H到平面的距离,即, ,
∽,,,
故平面EGF与平面的距离为.
9.(1)证明见解析;
(2)存在;.
【解析】
【分析】
(1)若选①,取中点,中点,中点,可证得四边形为平行四边形,从而利用勾股定理和平行关系证得,由线面垂直和面面垂直判定得到平面平面,利用面面垂直性质可证得平面;
若选②,取中点,中点,由线面垂直和面面垂直的判定可证得平面平面,利用面面垂直性质可证得平面;
若选③,取中点,中点,根据长度和平行关系可证得四边形为平行四边形,由此确定,得到,结合可得,从而利用勾股定理和平行关系证得,由线面垂直和面面垂直判定得到平面平面,利用面面垂直性质可证得平面;
三个条件均可说明两两互相垂直,则以为坐标原点可建立空间直角坐标系,利用面面垂直的向量证明方法可证得结论;
(2)假设存在满足题意的点,利用二面角的向量求法可构造方程求得,由此可确定点位置,得到的值.
(1)
若选①,取中点,中点,中点,连接,
,,四边形为平行四边形,,
,又,,,,
又,,又,,平面,
平面,平面,平面平面,
,,又平面,平面平面,
平面,又,,;
若选②,,,,平面,
平面,平面,平面平面,
取中点,中点,连接,
,,又平面,平面平面,
平面,又,,;
若选③,取中点,中点,连接,
,,又,;
分别为中点,,又,,
四边形为平行四边形,;
,,,,,
,,,
,又,,
又,,平面,
平面,平面,平面平面,
又,平面,平面平面,
平面,又,,;
综上所述:两两互相垂直,
则以为坐标原点,为轴,可建立如图所示空间直角坐标系,
则,,,,,
平面,平面的一个法向量;
设平面的法向量,
则,令,解得:,,,
,即,平面与平面.
(2)
设在线段上存在点,使得平面与平面夹角的余弦值等于,
由(1)得:,,
设平面的法向量,
则,令,则,,
;
,
化简可得:,解得:或(舍),
,,;
综上所述:在线段上存在点,满足,使得平面与平面夹角的余弦值等于.
10.(1)证明见解析;(2);(3).
【解析】
【分析】
(1)取的中点为,进而证明平面,然后根据面面垂直的判定定理得到答案;
(2)建立空间直角坐标系,进而根据空间向量的夹角公式求得答案;
(3)根据空间向量的坐标运算得出与间的关系式,进而求出的取值范围.
【详解】
(1)取的中点为,连接,.
由题意得,,
在中,因为为的中点,所以,即.
易得与全等,则,即.
因为,所以平面.
因为平面,所以平面平面.
(2)不妨设,由(1)平面,易知OB⊥AC,
如图,以为坐标原点,分别以,,所在直线为轴,轴,轴,建立空间直角坐标系,则,,,,,,,
设平面的法向量为,则得
不妨取,则.
因为,所以平面,所以平面的一个法向量为.
因为.
又二面角是锐二面角,所以二面角的余弦值为.
(3)结合(2)可得,,.
,
.
因为,所以,得.
即,是关于的单调递增函数,
当时,,故的取值范围是.
11.(1);(2);(3)
【解析】
【分析】
(1)由棱锥的体积计算即可;(2)取的中点,连接,可证明为二面角D-AB-C 的平面角,求出相关量可计算结果;(3)等体积法计算点到平面的距离,三元基本不等式求最值,求出距离的最大值.
【详解】
解:(1)该四面体可看作以为底面,以为高的三棱锥,DA=DB=a,
,所以为等边三角形,,
所以.
(2)取的中点,连接 则,因为,且DA=DB,所以,则,所以,则为二面角D-AB-C 的平面角.
因为,即,,,所以平面,即,又,,所以,所以,即二面角D-AB-C的大小为.
.
(3)三棱锥可看作以为底面,以为高的三棱锥,也可看作以为底面,为顶点的三棱锥,设到底面的距离为,则有.
由(2)可知,为等腰三角形,,则;即 ,解得:,令
当且仅当时等号成立,
所以
12.(1)
(2)
【解析】
【分析】
(1)求平面一个法向量,利用空间向量求点到线的距离公式求解;
(2)求平面得一个法向量,利用空间向量求线面角即可得解.
(1)
连接,∵,,∴,又平面,
以为原点,,,为,,轴建立空间直角坐标系,
则,,,,
由为的中点,知,
设,又,知,
则设平面一个法向量为,,
, 令,∴
所以点到平面的距离为
(2)
设平面一个法向量为,,
,令,∴
又,设直线与平面所成角为
,.
所以直线与平面所成角的余弦值为
13.(1);(2).
【解析】
【分析】
(1)取的中点,的中点,连接,,,可证明为二面角的平面角,根据长度关系,即得解;
(2)过点作交于点,在中,由余弦定理可得,设,由三角形相似可得,,在中,由余弦定理可得,
在、分别使用勾股定理,联立可得,结合,即得解.
【详解】
(1)取的中点,的中点,连接,,,
在中,,,则,
在等边中,,
故为二面角的平面角,
因为,所以,,,
则,所以,
则,故二面角的余弦值为;
(2)过点作交于点,
因为,则,又,所以,
在中,,
所以,设,则,
所以,,
在中,,
所以,因为,
则,
在中,①,
在中,②,
由①=②,可得,因为,所以,
故的取值范围为.
14.(1)证明见解析
(2)1
【解析】
【分析】
(1)设交于点连接,由,
并结合可证得平面由此证得,
再利用三角形相似证得从而证得平面进而证得平面平面;
(2)建立空间直角坐标系,设,
通过向量和平面的法向量建立直线与平面所成角的正弦值的关系式,并利用基本不等式,即可求最值.
(1)
证明:如图,设交于点连接,
易知,
又平面平面,
又平面.又是底面圆的内接正三角形,
由,可得,.又,,
即.又,,
,即.又平面,,
平面.又平面,平面平面.
(2)
易知.以点为坐标原点,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,
则,
设平面的法向量为,
则,即,令,则.设,
可得.
设直线与平面所成的角为,则.
令,,则
,当且仅当时,等号成立,
当时,有最大值,
于是当时,有最大值为,
的最大值为,
故直线与平面所成角的正弦值的最大值为.
15.(1)
(2)存在,点M位置为
【解析】
【分析】
(1)建立空间直角坐标系,利用向量法求二面角的余弦值;
(2)设,利用向量法求异面直线的夹角,得到,解方程即得解.
(1)
设是中点,为正三角形,则.
因为平面平面ABCD,平面平面,
又平面PAD,所以面ABCD.
又因为,,
所以为正三角形,所以,
以为原点,分别以为轴的正方向,建立空间直角坐标系,
则,,,,
于是,,.
设平面PEC的法向量为,
由即可取.
平面EBC的一个法向量为,
设二面角的平面角为,则
由图知为为钝角,所以二面角的余弦值为.
(2)
设,则,
,,
所以,
解得或0(舍),所以存在点M使得.
16.(1)证明见解析;(2).
【解析】
【分析】
(1)取,中点,,连接,,,得到面面,故可先将要证平面转化为求证面即可求证;
(2)可以通过建立空间直角坐标系,利用空间向量进行求解.
【详解】
(1)取,中点,,连接,,.
由,得,,
又,
所以平面.
由,知四边形是平行四边形,则,
平面,平面,所以平面,
同理平面,且,
所以平面平面,
所以平面.
(2)由,
知四边形是以的等腰梯形.
连接,则,
又平面,所以,
所以平面,又平面,
所以平面平面,
于是点在底面内的射影在上.
(在平面中,,点在以AC为直径的圆上运动)
取中点,则,
于是当底面时,四棱锥的体积最大.
如图,以为原点,分别以射线,,为,,轴的正半轴,
建立空间直角坐标系.
由题意得,,,
,.
所以,,.
设平面的法向量,
由,得,
取,则.
因此,直线与平面所成角的正弦值为.
17.(1)或
(2)
【解析】
【分析】
(1)建立空间直角坐标系,利用向量法列方程,化简求得的值.
(2)求得,,结合三角恒等变换求得,进而求得.
(1)
由于,所以,
在三角形中,由余弦定理得,
所以,所以,
依题意可知,
由于,所以平面,所以,.
以为空间坐标原点建立如图所示空间直角坐标系,
,
①当时:
,,
,
设平面的法向量为,
则,
故可设,
设平面的法向量为,
则
故可设,
由于平面平面,
所以,解得.
②当时,点与点重合,
平面(即平面)的法向量为,
设平面(即平面)的法向量为,
则,
故可设,
,即平面平面不成立,也即平面平面不成立.
③当时,点与点重合,
平面即平面,设平面即平面,
由于,所以平面.
由于平面,所以平面平面,也即平面平面成立.
综上所述,的为或.
(2)
①当时:
由(1)可知,平面的法向量为,
平面的法向量为,
所以.
,
所以.
,由于,所以.
②当时,点与点重合,,,
设平面的法向量为,
则,
故可设.
,.
,由于,所以.
综上所述,.
18.证明见解析.
【解析】
【分析】
利用长方体的特性可得,再利用三角恒等变换并结合三角函数性质即可得解.
【详解】
画出长方体,如图,
设,,,则、、均为锐角,
显然,则,
于是得,
而,则,即,同理,,因此,,
从而有,因,,
于是得,因此,,
综上得:,
所以.
19.(1)证明见解析;(2).
【解析】
【分析】
(1)作辅助线,利用线线平行或者面面平行,皆可证明线面平行.
(2) 先由AF⊥DE求出再根据直棱柱外接球半径的求法,即可求解.
【详解】
(1)证明∶取B1C1的中点G,连接DG,EF,FG,如图1,
则DG//A1B1,且;EF//AB,且,
又AB//A1B1,AB=A1B1,所以EF//DG,且EF= DG,
所以DEFG为平行四边形,所以DE//GF.
又平面 平面,
所以DE//平面
(注∶本题也可以取A1B1的中点H,连接DH,HE,利用平面DEH//平面B1BCC1来证DE//平面B1BCC1,如图2)
(2)解∶设,由已知,得,且,
则,
因为AF⊥DE,
所以,
解得,即
又AB=AC,则△ABC为等边三角形,
直三棱柱外接球的球心为△ABC与△A1B1C1中心连线O1O2的中点O,如图3,连接为直三棱柱ABC-A1B1C1外接球的半径.
因为,,所以,
所以直三棱柱外接球的表面积为
20.(1)证明见解析;(2).
【解析】
【分析】
(1)利用平面BB1C1C平面ACC1A1,,得到平面,又平面,得,由题意得,即可证明;
(2)利用等体积法,即可求解.
【详解】
(1)证明:∵正方形BB1C1C,,
∵面⊥面,面面,面,
∴B1C1⊥面ACC1A1,
又CM 面ACC1A1,∴B1C1⊥CM,
∵ACC1A1是菱形,,
∴为等边三角形,
∵M为A1C1中点,∴CM⊥A1C1,
又A1C1∩B1C1=C1,且A1C1,B1C1 面A1B1C1,
∴CM⊥面A1B1C1,
又CM 面MBC,
∴平面MBC⊥平面A1B1C1.
(2)解:由(1)可知,B1C1⊥面ACC1A1,
∴B1到平面MCC1的距离为B1C1=2,
由(1)知,CM⊥面A1B1C1,
∵MB1 面A1B1C1,∴CM⊥MB1,
在中,,
在中,,
,,
设点C1到平面MB1C的距离为h,
,
,
,
故点C1到平面MB1C的距离为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
