小学数学青岛版五四制四年级下册 2.2三角形的面积 课件(共20张PPT)
文档属性
| 名称 | 小学数学青岛版五四制四年级下册 2.2三角形的面积 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 615.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 09:48:25 | ||
图片预览





文档简介
(共20张PPT)
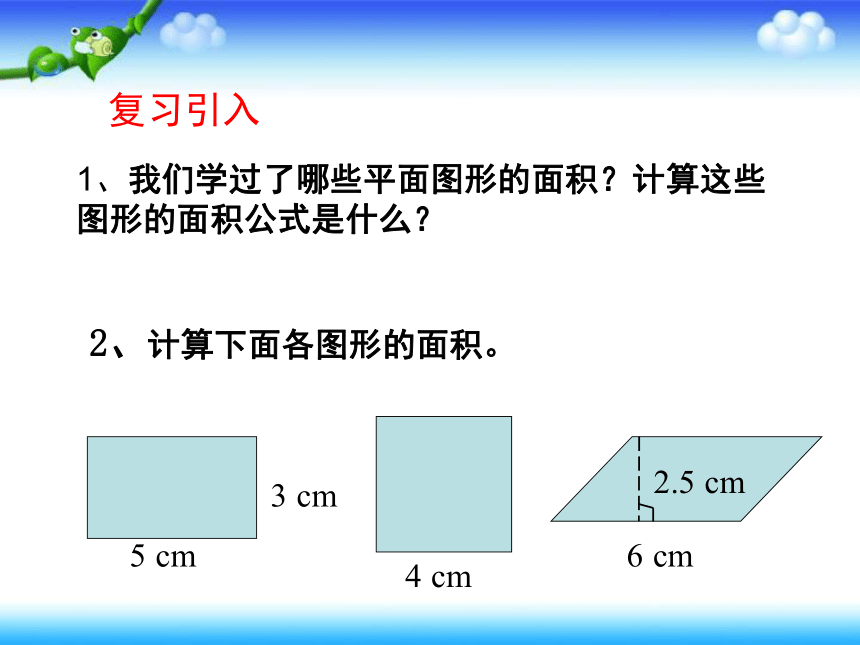
2、计算下面各图形的面积。
5 cm
3 cm
4 cm
6 cm
2.5 cm
1、我们学过了哪些平面图形的面积?计算这些图形的面积公式是什么?
复习引入
复习引入
3、平行四边形的面积是怎样推导出来的?用了什么思想?
把平行四边形割补成长方形。
用了转化的思想。
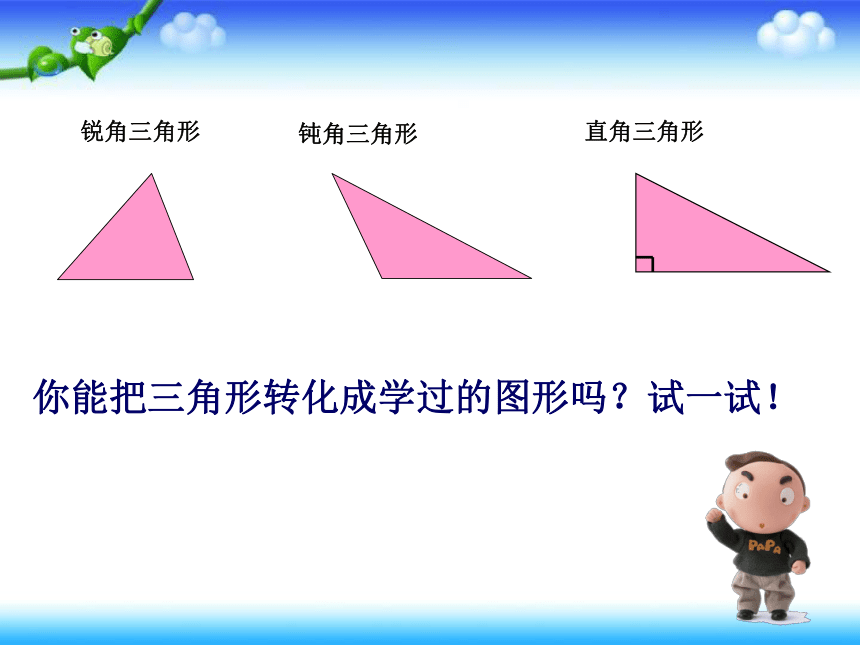
你能把三角形转化成学过的图形吗?试一试!
锐角三角形
钝角三角形
直角三角形
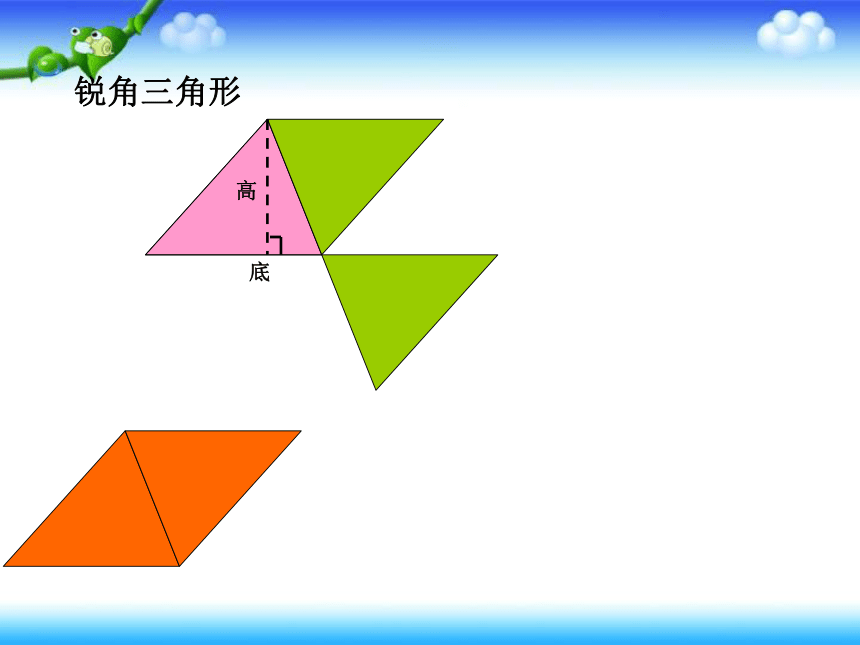
1、以小组为单位,拿出信封里的学具,用两个完全一样的三角形拼一拼,并思考:能拼出什么图形?看拼成的图形与原三角形有什么关系?
2、小组交流完成学习卡的填空。
小组活动:
通过试验,我发现:
1、两个完全一样的三角形可以拼成一个( )形。
2、拼成的平行四边形的底等于( )的底。
3、拼成的平行四边形的高等于( )的高。
4、每个三角形的面积就是这个平行四边形的( )。
所以,可以得出这样的结论:
三角形的面积=平行四边形面积÷( )
=( )×( )÷( )
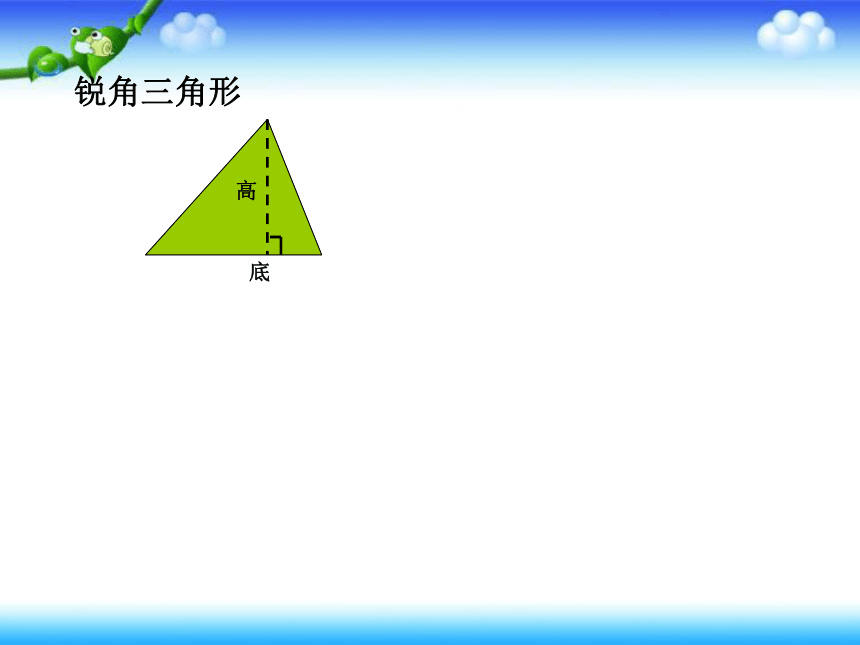
锐角三角形
底
高
锐角三角形
底
高
锐角三角形
底
高
锐角三角形
底
高
两个( )的三角形可以拼成一个( )
完全一样
高
底
平行四边形
锐角三角形
钝角三角形
直角三角形
长方形
正方形
通过试验,我发现:
1、两个完全一样的三角形可以拼成一个( )形。
2、拼成的平行四边形的底等于( )的底。
3、拼成的平行四边形的高等于( )的高。
4、每个三角形的面积等于这个平行四边形的( )。
所以,可以得出这样的结论:
三角形的面积=平行四边形面积÷( )
=( )×( )÷( )
平行四边
三角形
三角形
一半
底
高
2
2
底
高
底
三角形的面积 =
(平行四边形面积)
底 × 高
S = a h÷2
÷ 2
高
例2:红领巾的底是100cm, 高33cm,它的面积是多少平方厘米?
S = a h÷2
= 3300÷2
= 1650(c㎡)
答:它的面积是1650平方厘米。
= 100×33÷2
1、下面平行四边形的面积是12 cm2,求涂色的三角形的面积。
S=12÷2
=6(cm2)
三、巩固运用,解决问题
答:涂色的三角形的面积是6平方厘米。
2、一种三角尺的形状如下图,它的面积是多少?
S=ah÷2
=12.5×7.2÷2
=45(cm2)
三、巩固运用,解决问题
答:它的面积是45平方厘米。
3、一个三角形的底是8厘米,高是底的2倍,它的面积是多少平方厘米?
高:8×2=16(cm)
S=ah÷2
=8×16÷2
=64(cm2)
答:它的面积是64平方厘米。
2、三角形面积是8d㎡,
1、两个 的三角形可以拼成一个平行四边形。( )
面积相等
完全一样
与它等底等高的平行四边形面积是16d㎡ 。
( )
3、
( )
那么平行四边形面积是16d㎡。
6
5
5.4
单位:cm
这个三角形的面积列式为:
6×5.4÷2
5×5.4÷2
底
高
4、一面三角形小旗的底是3dm,高是1.5dm,两面这样的小旗面积
一共是
3×1.5=4.5( d㎡ )
( )
√
4、判断对错
课堂小结
你学会了那些知识
2、计算下面各图形的面积。
5 cm
3 cm
4 cm
6 cm
2.5 cm
1、我们学过了哪些平面图形的面积?计算这些图形的面积公式是什么?
复习引入
复习引入
3、平行四边形的面积是怎样推导出来的?用了什么思想?
把平行四边形割补成长方形。
用了转化的思想。
你能把三角形转化成学过的图形吗?试一试!
锐角三角形
钝角三角形
直角三角形
1、以小组为单位,拿出信封里的学具,用两个完全一样的三角形拼一拼,并思考:能拼出什么图形?看拼成的图形与原三角形有什么关系?
2、小组交流完成学习卡的填空。
小组活动:
通过试验,我发现:
1、两个完全一样的三角形可以拼成一个( )形。
2、拼成的平行四边形的底等于( )的底。
3、拼成的平行四边形的高等于( )的高。
4、每个三角形的面积就是这个平行四边形的( )。
所以,可以得出这样的结论:
三角形的面积=平行四边形面积÷( )
=( )×( )÷( )
锐角三角形
底
高
锐角三角形
底
高
锐角三角形
底
高
锐角三角形
底
高
两个( )的三角形可以拼成一个( )
完全一样
高
底
平行四边形
锐角三角形
钝角三角形
直角三角形
长方形
正方形
通过试验,我发现:
1、两个完全一样的三角形可以拼成一个( )形。
2、拼成的平行四边形的底等于( )的底。
3、拼成的平行四边形的高等于( )的高。
4、每个三角形的面积等于这个平行四边形的( )。
所以,可以得出这样的结论:
三角形的面积=平行四边形面积÷( )
=( )×( )÷( )
平行四边
三角形
三角形
一半
底
高
2
2
底
高
底
三角形的面积 =
(平行四边形面积)
底 × 高
S = a h÷2
÷ 2
高
例2:红领巾的底是100cm, 高33cm,它的面积是多少平方厘米?
S = a h÷2
= 3300÷2
= 1650(c㎡)
答:它的面积是1650平方厘米。
= 100×33÷2
1、下面平行四边形的面积是12 cm2,求涂色的三角形的面积。
S=12÷2
=6(cm2)
三、巩固运用,解决问题
答:涂色的三角形的面积是6平方厘米。
2、一种三角尺的形状如下图,它的面积是多少?
S=ah÷2
=12.5×7.2÷2
=45(cm2)
三、巩固运用,解决问题
答:它的面积是45平方厘米。
3、一个三角形的底是8厘米,高是底的2倍,它的面积是多少平方厘米?
高:8×2=16(cm)
S=ah÷2
=8×16÷2
=64(cm2)
答:它的面积是64平方厘米。
2、三角形面积是8d㎡,
1、两个 的三角形可以拼成一个平行四边形。( )
面积相等
完全一样
与它等底等高的平行四边形面积是16d㎡ 。
( )
3、
( )
那么平行四边形面积是16d㎡。
6
5
5.4
单位:cm
这个三角形的面积列式为:
6×5.4÷2
5×5.4÷2
底
高
4、一面三角形小旗的底是3dm,高是1.5dm,两面这样的小旗面积
一共是
3×1.5=4.5( d㎡ )
( )
√
4、判断对错
课堂小结
你学会了那些知识
