2021-2022学年人教版九年级数学下册 第二十九章投影与视图单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册 第二十九章投影与视图单元测试训练卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 196.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 10:07:38 | ||
图片预览


文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
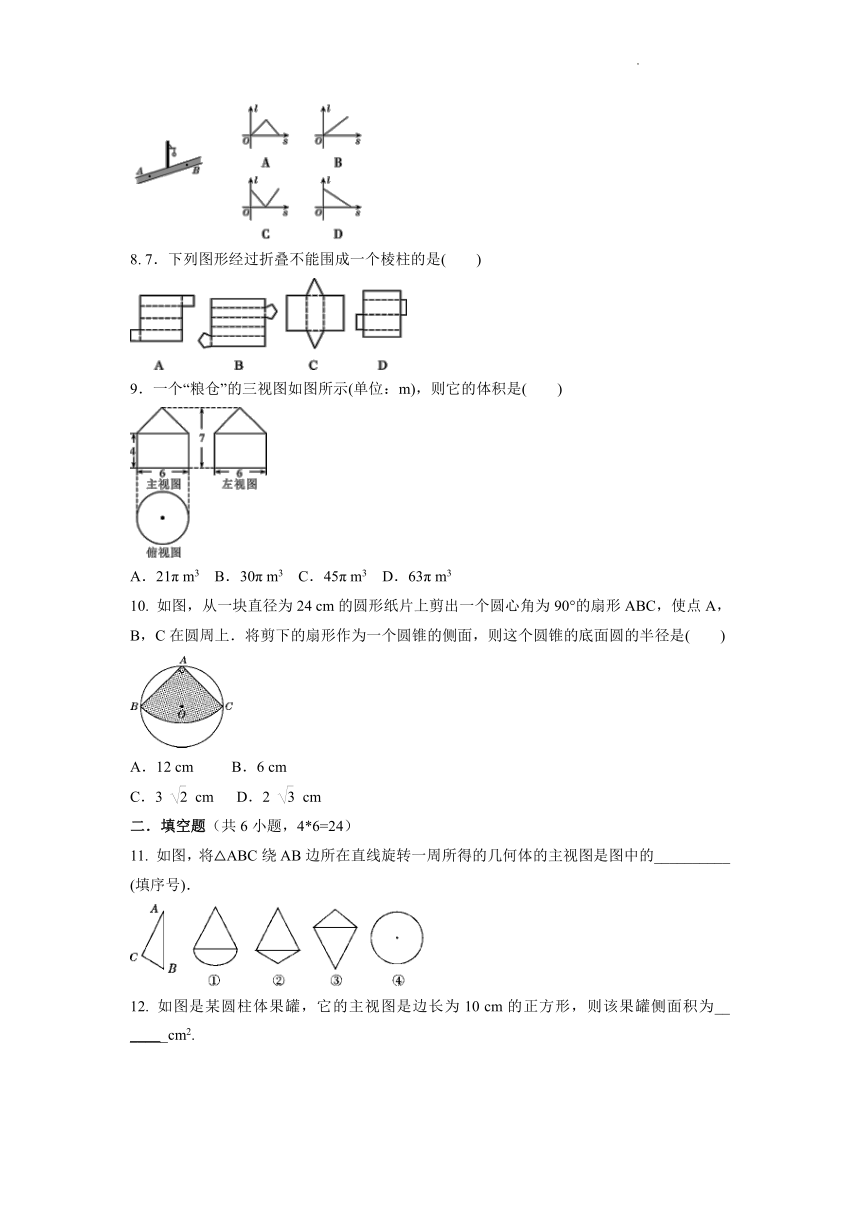
1. 下面四个立体图形中,主视图是三角形的是( )
2. 下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A B C D
3. 如图,将一个小球摆放在圆柱上底面的正中间,则该几何体的俯视图是( )
4. 某几何体的左视图如图所示,则该几何体不可能是( )
5. 图中三视图对应的正三棱柱是( )
6. 如图,下列选项中不是正六棱柱三视图的是( )
7. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图像刻画出来,大致是( )
8. 7.下列图形经过折叠不能围成一个棱柱的是( )
9.一个“粮仓”的三视图如图所示(单位:m),则它的体积是( )
A.21π m3 B.30π m3 C.45π m3 D.63π m3
10. 如图,从一块直径为24 cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.12 cm B.6 cm
C.3 cm D.2 cm
二.填空题(共6小题,4*6=24)
11. 如图,将△ABC绕AB边所在直线旋转一周所得的几何体的主视图是图中的__________ (填序号).
12. 如图是某圆柱体果罐,它的主视图是边长为10 cm的正方形,则该果罐侧面积为__ _____cm2.
13. 如图,若圆锥的高为,高与母线的夹角为30°,则圆锥的侧面积为________.
14. 如图,太阳光线与地面成的角,照在地面的一只排球上,排球在地面的投影长是,则排球的直径是______ cm.
15. 某长方体包装盒的展开图如图所示,如果长方体盒子的长比宽多4cm,则这个包装盒的体积是________ cm3 .
16.如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要________个小正方体,王亮所搭几何体的表面积为________.
三.解答题(共5小题, 56分)
17.(6分) 如图所示画出的两个图形都是一个圆柱体的正投影,试判断正误,并说明原因.
18.(8分) 如图,某一广告墙PQ旁有两根直立的木杆AB和CD,某一时刻在太阳光下,木杆CD的影子刚好不落在广告墙PQ上.
(1)请在图中画出此时的太阳光线CE及木杆AB的影子BF;
(2)若AB=5米,CD=3米,CD到PQ的距离DQ的长为4米,求此时木杆AB的影长.
19.(8分) 如图所示为一几何体的三视图.
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若三视图中的长方形的长为10 cm,正三角形的边长为4 cm,求这个几何体的侧面积.
20.(10分) 如图是一个由若干个同样大小的正方体搭成的几何体的俯视图,正方形中的数字表示在该位置的正方体的个数.
(1)请你画出该几何体的主视图和左视图;
(2)如果每个正方体的棱长为2 cm,则该几何体的表面积是多少?
21.(12分) 如图是用矩形厚纸片(厚度不计)做长方体包装盒的示意图,阴影部分是裁剪掉的部分.沿图中实线折叠做成的长方体纸盒的上下底面是正方形,有三处矩形形状的“舌头”用来折叠后粘贴或封盖.
(1)若用长31cm,宽26cm的矩形厚纸片,恰好能做成一个符合要求的包装盒,盒高是盒底边长的2.5倍,三处“舌头”的宽度相等.求“舌头”的宽度和纸盒的高度;
(2)现有一张40cm×35cm的矩形厚纸片,按如图所示的方法设计包装盒,用来包装一个圆柱形工艺笔筒,已知该种笔筒的高是底面直径的2.5倍,要求包装盒“舌头”的宽度为2cm(如有多余可裁剪),问这样的笔筒底面直径最大可以为多少?
22.(12分) 图①是一个三棱柱包装盒,它的底面是边长为10 cm的正三角形,三个侧面都是矩形.现将宽为15 cm的彩色矩形纸带AMCN沿虚线裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算∠BAD的度数;
(2)计算按图③的方式包这个三棱柱包装盒所需的矩形纸带的长度.
② ③
参考答案
1-5CBCDA 6-10BCDCC
11.②
12.100π
13.2π
14. 21
15.90
16.19,48
17. 解:图①是错误的;图②是正确的.因为圆柱体的正投影是平行光线的投影,投影线与投影面是垂直的,所以投影后不可能是圆柱,而是一个平面图形——矩形或正方形.
18.解:(1)如图所示.
(2)设木杆AB的影长BF为x米,由题意得=,解得x=.答:木杆AB的影长是米.
19. 解:(1)这个几何体是正三棱柱.
(2)如图所示.(答案不唯一)
(3)S侧=3×4×10=120(cm2).
20. 解:(1)如图所示.
(2)该几何体的表面积是(2×2)×(6×2+6×2+5×2+4)=4×38=152(cm2).
21. (1)设纸盒底面边长为acm,“舌头”的宽为bcm.由题意可得:解得:2.5×6=15cm,答:“舌头”的宽度为2cm,纸盒的高度为15cm; (2)直径最大可以是8cm.
22. 解:(1)AB的长等于三棱柱的底面周长,为30 cm.∵纸带的宽为15 cm,∴sin ∠DAB=sin ∠ABM===,∴∠DAB=30°.
(2)在题图中,将三棱柱沿过点A的侧棱剪开,得到如图所示的侧面展开图.将△ABE向左平移30 cm,△CDF向右平移30 cm,拼成如图所示的平行四边形A′B′C′D′.此平行四边形即为题图②中的平行四边形ABCD.易得AC′=2AE=2×=40(cm),∴在题图②中,BC=40cm,∴所需矩形纸带的长度为MB+BC=30·cos30°+40=55(cm).
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下面四个立体图形中,主视图是三角形的是( )
2. 下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A B C D
3. 如图,将一个小球摆放在圆柱上底面的正中间,则该几何体的俯视图是( )
4. 某几何体的左视图如图所示,则该几何体不可能是( )
5. 图中三视图对应的正三棱柱是( )
6. 如图,下列选项中不是正六棱柱三视图的是( )
7. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图像刻画出来,大致是( )
8. 7.下列图形经过折叠不能围成一个棱柱的是( )
9.一个“粮仓”的三视图如图所示(单位:m),则它的体积是( )
A.21π m3 B.30π m3 C.45π m3 D.63π m3
10. 如图,从一块直径为24 cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.12 cm B.6 cm
C.3 cm D.2 cm
二.填空题(共6小题,4*6=24)
11. 如图,将△ABC绕AB边所在直线旋转一周所得的几何体的主视图是图中的__________ (填序号).
12. 如图是某圆柱体果罐,它的主视图是边长为10 cm的正方形,则该果罐侧面积为__ _____cm2.
13. 如图,若圆锥的高为,高与母线的夹角为30°,则圆锥的侧面积为________.
14. 如图,太阳光线与地面成的角,照在地面的一只排球上,排球在地面的投影长是,则排球的直径是______ cm.
15. 某长方体包装盒的展开图如图所示,如果长方体盒子的长比宽多4cm,则这个包装盒的体积是________ cm3 .
16.如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要________个小正方体,王亮所搭几何体的表面积为________.
三.解答题(共5小题, 56分)
17.(6分) 如图所示画出的两个图形都是一个圆柱体的正投影,试判断正误,并说明原因.
18.(8分) 如图,某一广告墙PQ旁有两根直立的木杆AB和CD,某一时刻在太阳光下,木杆CD的影子刚好不落在广告墙PQ上.
(1)请在图中画出此时的太阳光线CE及木杆AB的影子BF;
(2)若AB=5米,CD=3米,CD到PQ的距离DQ的长为4米,求此时木杆AB的影长.
19.(8分) 如图所示为一几何体的三视图.
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若三视图中的长方形的长为10 cm,正三角形的边长为4 cm,求这个几何体的侧面积.
20.(10分) 如图是一个由若干个同样大小的正方体搭成的几何体的俯视图,正方形中的数字表示在该位置的正方体的个数.
(1)请你画出该几何体的主视图和左视图;
(2)如果每个正方体的棱长为2 cm,则该几何体的表面积是多少?
21.(12分) 如图是用矩形厚纸片(厚度不计)做长方体包装盒的示意图,阴影部分是裁剪掉的部分.沿图中实线折叠做成的长方体纸盒的上下底面是正方形,有三处矩形形状的“舌头”用来折叠后粘贴或封盖.
(1)若用长31cm,宽26cm的矩形厚纸片,恰好能做成一个符合要求的包装盒,盒高是盒底边长的2.5倍,三处“舌头”的宽度相等.求“舌头”的宽度和纸盒的高度;
(2)现有一张40cm×35cm的矩形厚纸片,按如图所示的方法设计包装盒,用来包装一个圆柱形工艺笔筒,已知该种笔筒的高是底面直径的2.5倍,要求包装盒“舌头”的宽度为2cm(如有多余可裁剪),问这样的笔筒底面直径最大可以为多少?
22.(12分) 图①是一个三棱柱包装盒,它的底面是边长为10 cm的正三角形,三个侧面都是矩形.现将宽为15 cm的彩色矩形纸带AMCN沿虚线裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算∠BAD的度数;
(2)计算按图③的方式包这个三棱柱包装盒所需的矩形纸带的长度.
② ③
参考答案
1-5CBCDA 6-10BCDCC
11.②
12.100π
13.2π
14. 21
15.90
16.19,48
17. 解:图①是错误的;图②是正确的.因为圆柱体的正投影是平行光线的投影,投影线与投影面是垂直的,所以投影后不可能是圆柱,而是一个平面图形——矩形或正方形.
18.解:(1)如图所示.
(2)设木杆AB的影长BF为x米,由题意得=,解得x=.答:木杆AB的影长是米.
19. 解:(1)这个几何体是正三棱柱.
(2)如图所示.(答案不唯一)
(3)S侧=3×4×10=120(cm2).
20. 解:(1)如图所示.
(2)该几何体的表面积是(2×2)×(6×2+6×2+5×2+4)=4×38=152(cm2).
21. (1)设纸盒底面边长为acm,“舌头”的宽为bcm.由题意可得:解得:2.5×6=15cm,答:“舌头”的宽度为2cm,纸盒的高度为15cm; (2)直径最大可以是8cm.
22. 解:(1)AB的长等于三棱柱的底面周长,为30 cm.∵纸带的宽为15 cm,∴sin ∠DAB=sin ∠ABM===,∴∠DAB=30°.
(2)在题图中,将三棱柱沿过点A的侧棱剪开,得到如图所示的侧面展开图.将△ABE向左平移30 cm,△CDF向右平移30 cm,拼成如图所示的平行四边形A′B′C′D′.此平行四边形即为题图②中的平行四边形ABCD.易得AC′=2AE=2×=40(cm),∴在题图②中,BC=40cm,∴所需矩形纸带的长度为MB+BC=30·cos30°+40=55(cm).
