新疆维吾尔自治区喀什第二高级中学2021-2022学年高一下学期2月开学考试数学试题(Word版含答案)
文档属性
| 名称 | 新疆维吾尔自治区喀什第二高级中学2021-2022学年高一下学期2月开学考试数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 351.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-03 12:49:15 | ||
图片预览

文档简介
喀什第二高级中学2021-2022学年高一下学期2月开学考试
数学
本卷满分150分,考试时间120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1.设全集,,,则()
A. B. C. D.
2.已知,为实数,则“,”是“”的()
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知,,,则()
A. B. C. D.
4.下列命题:
①对立事件一定是互斥事件;②若A,B为两个随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
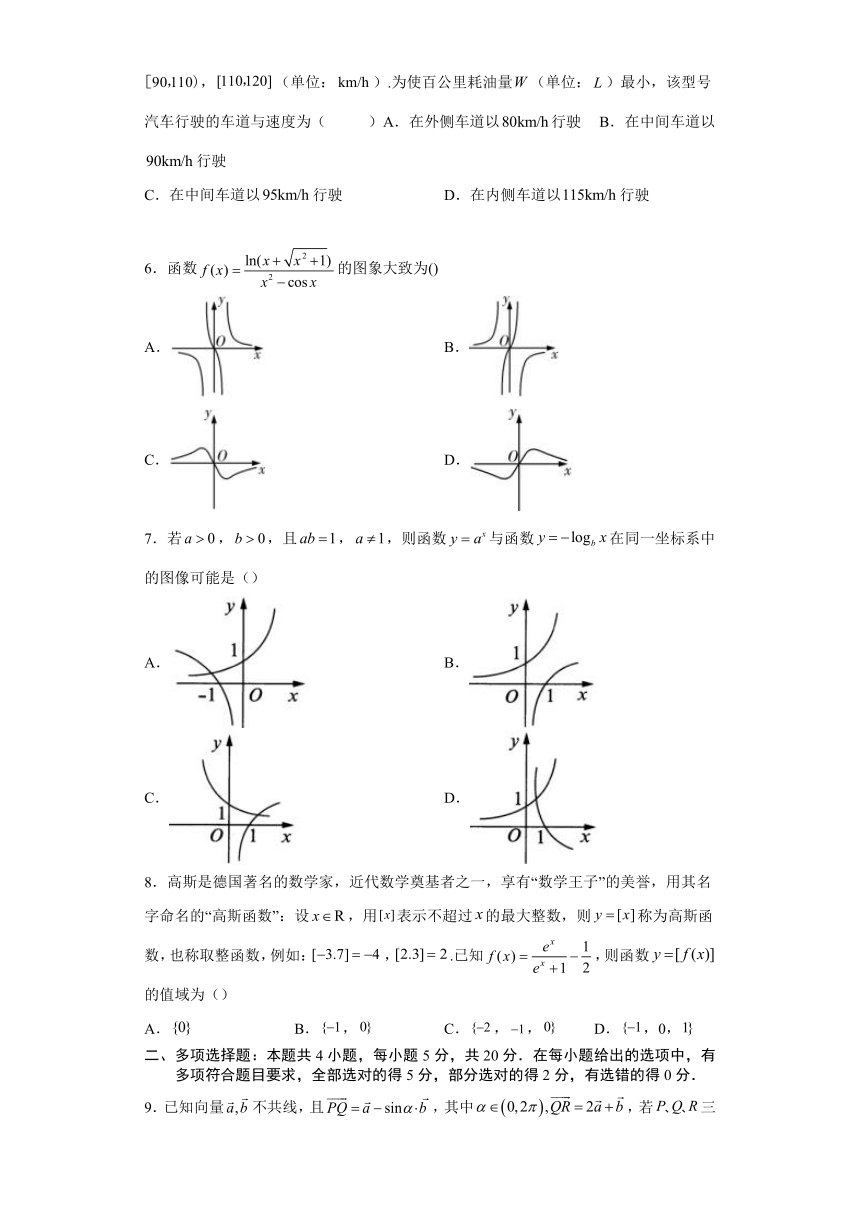
5..经多次实验得到某种型号的汽车每小时耗油量(单位:)与速度(单位:)()的数据如下表:
40 60 90 100 120
5.2 6 8.325 10 15.6
为描述与的关系,现有以下三种模型供选择:,,.选出最符合实际的函数模型,解决下列问题:某高速公路共有三个车道,分别是外侧车道、中间车道、内侧车道,车速范围分别是,,(单位:).为使百公里耗油量(单位:)最小,该型号汽车行驶的车道与速度为( )A.在外侧车道以行驶 B.在中间车道以行驶
C.在中间车道以行驶 D.在内侧车道以行驶
6.函数的图象大致为()
A. B.
C. D.
7.若,,且,,则函数与函数在同一坐标系中的图像可能是()
A. B.
C. D.
8.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的美誉,用其名字命名的“高斯函数”:设,用表示不超过的最大整数,则称为高斯函数,也称取整函数,例如:,.已知,则函数的值域为()
A. B., C.,, D.,0,
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
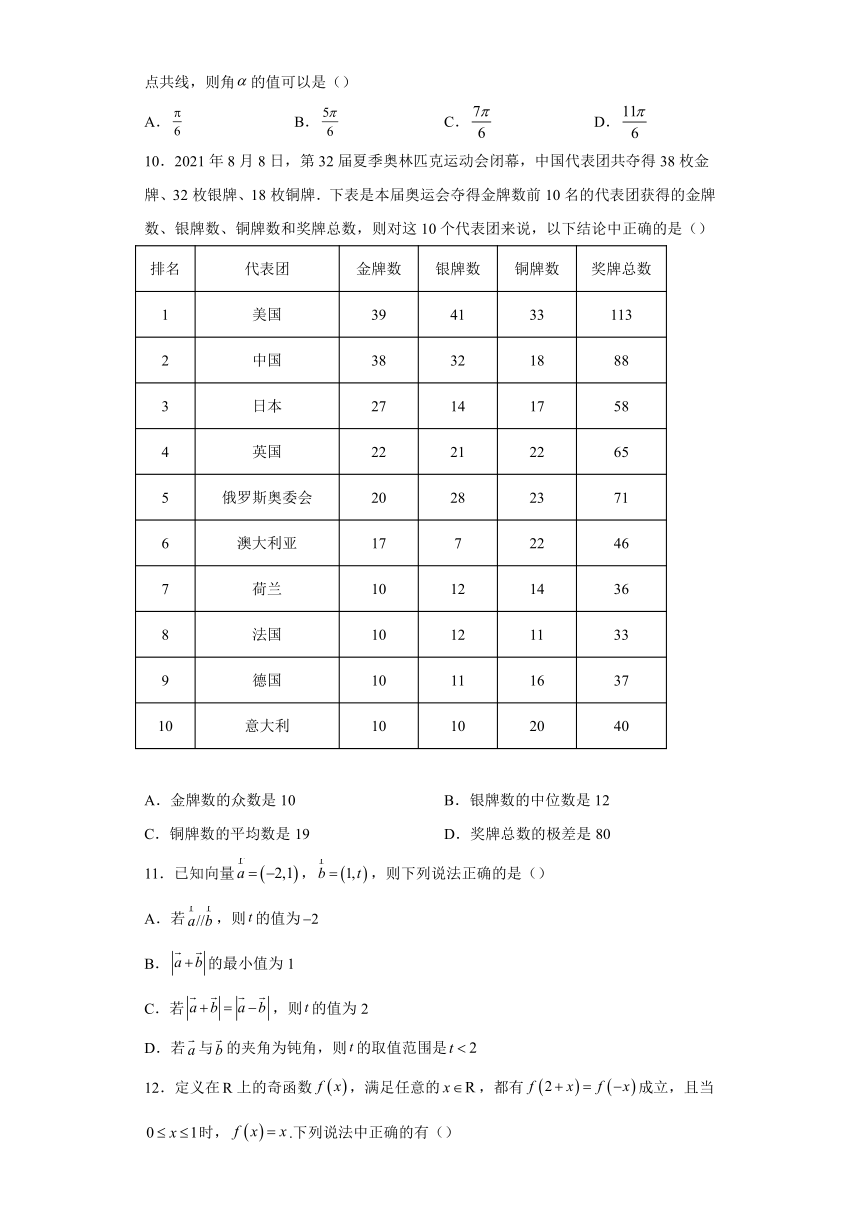
9.已知向量不共线,且,其中,若三点共线,则角的值可以是()
A. B. C. D.
10.2021年8月8日,第32届夏季奥林匹克运动会闭幕,中国代表团共夺得38枚金牌、32枚银牌、18枚铜牌.下表是本届奥运会夺得金牌数前10名的代表团获得的金牌数、银牌数、铜牌数和奖牌总数,则对这10个代表团来说,以下结论中正确的是()
排名 代表团 金牌数 银牌数 铜牌数 奖牌总数
1 美国 39 41 33 113
2 中国 38 32 18 88
3 日本 27 14 17 58
4 英国 22 21 22 65
5 俄罗斯奥委会 20 28 23 71
6 澳大利亚 17 7 22 46
7 荷兰 10 12 14 36
8 法国 10 12 11 33
9 德国 10 11 16 37
10 意大利 10 10 20 40
A.金牌数的众数是10 B.银牌数的中位数是12
C.铜牌数的平均数是19 D.奖牌总数的极差是80
11.已知向量,,则下列说法正确的是()
A.若,则的值为
B.的最小值为1
C.若,则的值为2
D.若与的夹角为钝角,则的取值范围是
12.定义在上的奇函数,满足任意的,都有成立,且当时,.下列说法中正确的有()
A.函数为周期函数
B.函数的对称中心为
C.当时,函数的图象与轴围成图形的面积为平方单位
D.
三、填空题:本题共4小题,每小题5分,共20分.
13.某单位开展“党员在线学习”活动,统计某党员7月份学习得分情况,下表是随机抽取该党员七天学习得分情况:
日期 7月2日 7月6日 7月13日 7月15日 7月16日 7月19日 7月21日
得分 35 26 15 20 30 25 17
则所抽取的样本(七天学习得分)的均值为______;据此,可以估计该党员7月份学习得分的均值为______.
14.给出下列命题:
①;②;③;④如果两个角的和等于180°,那么这两个角互为邻补角.正确的是_______
15.袋中装有一些大小相同的球,其中标号为1号的球1个,标号为2号的球2个,标号为3号的球3个,,标号为号的球个.现从袋中任取一球,所得号数为随机变量,若,则______.
16.若对任意的,,且当时,都有,则的最小值是________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.计算下列各式的值.
(1);
(2).
18.年月日,中国向世界庄严宣告,中国脱贫攻坚战取得了全面胜利,现行标准下万农村贫困人口全部脱贫,个贫困县全部摘帽,万个贫困村全部出列,区域性整体贫困得到解决,完成了消除绝对贫困的艰巨任务,困扰中华民族几千年的绝对贫困问题得到了历史性的解决!为了巩固脱贫成果,某农科所实地考察,研究发现某脱贫村适合种植、两种经济作物,可以通过种植这两种经济作物巩固脱贫成果,通过大量考察研究得到如下统计数据:经济作物的亩产量约为公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
年份编号
年份
单价(元/公斤)
经济作物的收购价格始终为元/公斤,其亩产量的频率分布直方图如下:
(1)若经济作物的单价(单位:元/公斤)与年份编号具有线性相关关系,请求出关于的回归直线方程,并估计年经济作物的单价;
(2)用上述频率分布直方图估计经济作物的平均亩产量(每组数据以区间的中点值为代表),若不考虑其他因素,试判断年该村应种植经济作物还是经济作物?并说明理由.
附:,.
19.已知幂函数的图象经过点
(1)试确定m的值;
(2)判断该函数的奇偶性并证明;
(3)求满足条件的实数a的取值范围.
20.如图,过函数的图象上的两点A,B分别作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数(m>c>1)的图象交于点C,且AC垂直于y轴.
(1)当a=2,b=4,c=3时,求实数m的值;
(2)当b=a2时,求的最大值.
21.如图,四边形ABCD中,已知.
(1)用,表示;
(2)若,,用,表示.
22.若函数、都在区间I上有定义,对任意都有成立,则称、为区间I上的“均分函数”.
(1)判断、是否为区间上的“均分函数”,并说明理由;
(2)若、为区间上的“均分函数”,求m的取值范围;
(3)若、为区间上的“均分函数”,求k的取值范围.
试卷第1页,共3页
喀什第二高级中学2021-2022学年高一下学期2月开学考试
数学答案
C2.A 3.A 4.A 5.A 6.A 7.B 8.B 9.CD 10.AD 11.BC 12.ACD
13.24.24. 14.③ 15.9 16.2
17.(1)2
(2)
18.(1),元/公斤;(2)应该种植经济作物;理由见解析.
19.(1)
(2)奇函数,证明见解析
(3)
20.(1)9;(2)的最大值为1.
21.(1);(2).
22.(1)是均分函数,理由见解析;
(2);
(3).
数学
本卷满分150分,考试时间120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1.设全集,,,则()
A. B. C. D.
2.已知,为实数,则“,”是“”的()
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知,,,则()
A. B. C. D.
4.下列命题:
①对立事件一定是互斥事件;②若A,B为两个随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
5..经多次实验得到某种型号的汽车每小时耗油量(单位:)与速度(单位:)()的数据如下表:
40 60 90 100 120
5.2 6 8.325 10 15.6
为描述与的关系,现有以下三种模型供选择:,,.选出最符合实际的函数模型,解决下列问题:某高速公路共有三个车道,分别是外侧车道、中间车道、内侧车道,车速范围分别是,,(单位:).为使百公里耗油量(单位:)最小,该型号汽车行驶的车道与速度为( )A.在外侧车道以行驶 B.在中间车道以行驶
C.在中间车道以行驶 D.在内侧车道以行驶
6.函数的图象大致为()
A. B.
C. D.
7.若,,且,,则函数与函数在同一坐标系中的图像可能是()
A. B.
C. D.
8.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的美誉,用其名字命名的“高斯函数”:设,用表示不超过的最大整数,则称为高斯函数,也称取整函数,例如:,.已知,则函数的值域为()
A. B., C.,, D.,0,
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知向量不共线,且,其中,若三点共线,则角的值可以是()
A. B. C. D.
10.2021年8月8日,第32届夏季奥林匹克运动会闭幕,中国代表团共夺得38枚金牌、32枚银牌、18枚铜牌.下表是本届奥运会夺得金牌数前10名的代表团获得的金牌数、银牌数、铜牌数和奖牌总数,则对这10个代表团来说,以下结论中正确的是()
排名 代表团 金牌数 银牌数 铜牌数 奖牌总数
1 美国 39 41 33 113
2 中国 38 32 18 88
3 日本 27 14 17 58
4 英国 22 21 22 65
5 俄罗斯奥委会 20 28 23 71
6 澳大利亚 17 7 22 46
7 荷兰 10 12 14 36
8 法国 10 12 11 33
9 德国 10 11 16 37
10 意大利 10 10 20 40
A.金牌数的众数是10 B.银牌数的中位数是12
C.铜牌数的平均数是19 D.奖牌总数的极差是80
11.已知向量,,则下列说法正确的是()
A.若,则的值为
B.的最小值为1
C.若,则的值为2
D.若与的夹角为钝角,则的取值范围是
12.定义在上的奇函数,满足任意的,都有成立,且当时,.下列说法中正确的有()
A.函数为周期函数
B.函数的对称中心为
C.当时,函数的图象与轴围成图形的面积为平方单位
D.
三、填空题:本题共4小题,每小题5分,共20分.
13.某单位开展“党员在线学习”活动,统计某党员7月份学习得分情况,下表是随机抽取该党员七天学习得分情况:
日期 7月2日 7月6日 7月13日 7月15日 7月16日 7月19日 7月21日
得分 35 26 15 20 30 25 17
则所抽取的样本(七天学习得分)的均值为______;据此,可以估计该党员7月份学习得分的均值为______.
14.给出下列命题:
①;②;③;④如果两个角的和等于180°,那么这两个角互为邻补角.正确的是_______
15.袋中装有一些大小相同的球,其中标号为1号的球1个,标号为2号的球2个,标号为3号的球3个,,标号为号的球个.现从袋中任取一球,所得号数为随机变量,若,则______.
16.若对任意的,,且当时,都有,则的最小值是________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.计算下列各式的值.
(1);
(2).
18.年月日,中国向世界庄严宣告,中国脱贫攻坚战取得了全面胜利,现行标准下万农村贫困人口全部脱贫,个贫困县全部摘帽,万个贫困村全部出列,区域性整体贫困得到解决,完成了消除绝对贫困的艰巨任务,困扰中华民族几千年的绝对贫困问题得到了历史性的解决!为了巩固脱贫成果,某农科所实地考察,研究发现某脱贫村适合种植、两种经济作物,可以通过种植这两种经济作物巩固脱贫成果,通过大量考察研究得到如下统计数据:经济作物的亩产量约为公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
年份编号
年份
单价(元/公斤)
经济作物的收购价格始终为元/公斤,其亩产量的频率分布直方图如下:
(1)若经济作物的单价(单位:元/公斤)与年份编号具有线性相关关系,请求出关于的回归直线方程,并估计年经济作物的单价;
(2)用上述频率分布直方图估计经济作物的平均亩产量(每组数据以区间的中点值为代表),若不考虑其他因素,试判断年该村应种植经济作物还是经济作物?并说明理由.
附:,.
19.已知幂函数的图象经过点
(1)试确定m的值;
(2)判断该函数的奇偶性并证明;
(3)求满足条件的实数a的取值范围.
20.如图,过函数的图象上的两点A,B分别作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数(m>c>1)的图象交于点C,且AC垂直于y轴.
(1)当a=2,b=4,c=3时,求实数m的值;
(2)当b=a2时,求的最大值.
21.如图,四边形ABCD中,已知.
(1)用,表示;
(2)若,,用,表示.
22.若函数、都在区间I上有定义,对任意都有成立,则称、为区间I上的“均分函数”.
(1)判断、是否为区间上的“均分函数”,并说明理由;
(2)若、为区间上的“均分函数”,求m的取值范围;
(3)若、为区间上的“均分函数”,求k的取值范围.
试卷第1页,共3页
喀什第二高级中学2021-2022学年高一下学期2月开学考试
数学答案
C2.A 3.A 4.A 5.A 6.A 7.B 8.B 9.CD 10.AD 11.BC 12.ACD
13.24.24. 14.③ 15.9 16.2
17.(1)2
(2)
18.(1),元/公斤;(2)应该种植经济作物;理由见解析.
19.(1)
(2)奇函数,证明见解析
(3)
20.(1)9;(2)的最大值为1.
21.(1);(2).
22.(1)是均分函数,理由见解析;
(2);
(3).
同课章节目录
