苏科版七年级数学下册 11.4 解一元一次不等式 课件(共18张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 11.4 解一元一次不等式 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 06:03:00 | ||
图片预览


文档简介
(共18张PPT)
解一元一次不等式组
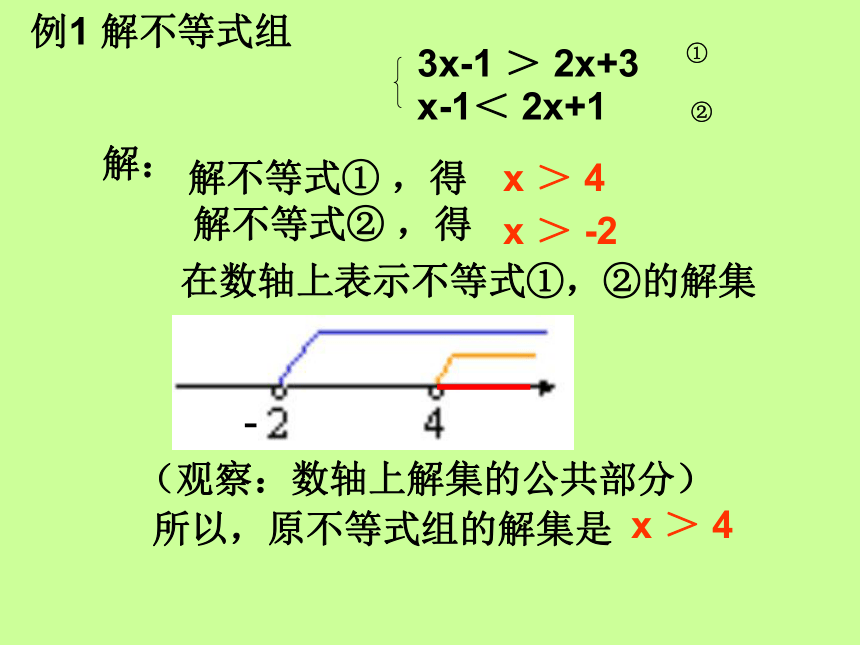
例1 解不等式组
3x-1 > 2x+3
x-1< 2x+1 ②
①
解:
解不等式① ,得
解不等式② ,得
x > 4
x > -2
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
x > 4
(观察:数轴上解集的公共部分)
-
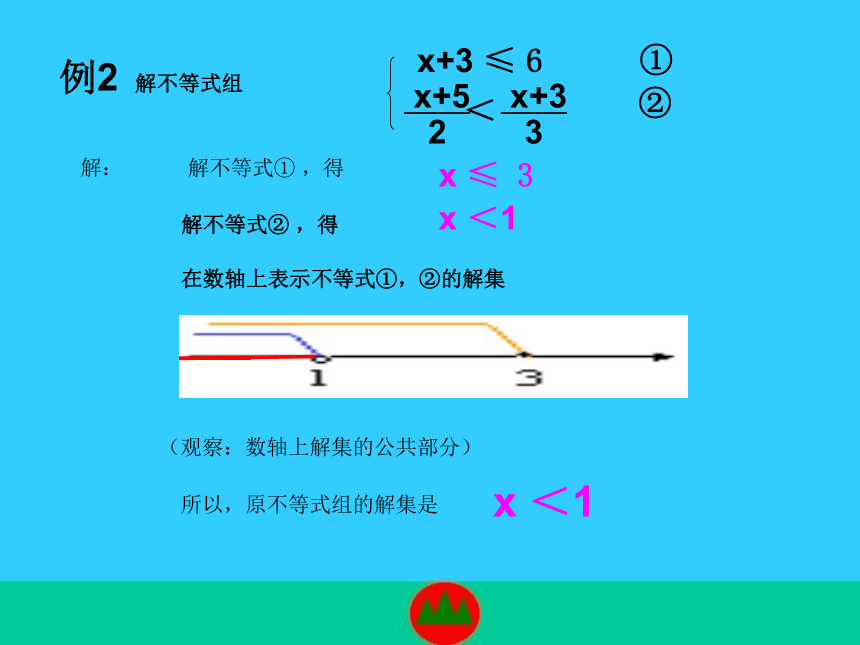
例2 解不等式组
x+3 ≤ 6
①
解:
解不等式① ,得
解不等式② ,得
x ≤ 3
x <1
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
(观察:数轴上解集的公共部分)
②
x <1
x+5
2
<
x+3
3
例3 解不等式组
2x+3 <5
3x-2 >4 ②
①
解:
解不等式① ,得
解不等式② ,得
x < 1
x > 2
在数轴上表示不等式①,②的解集
所以,原不等组无解
(观察:数轴上有无公共部分)
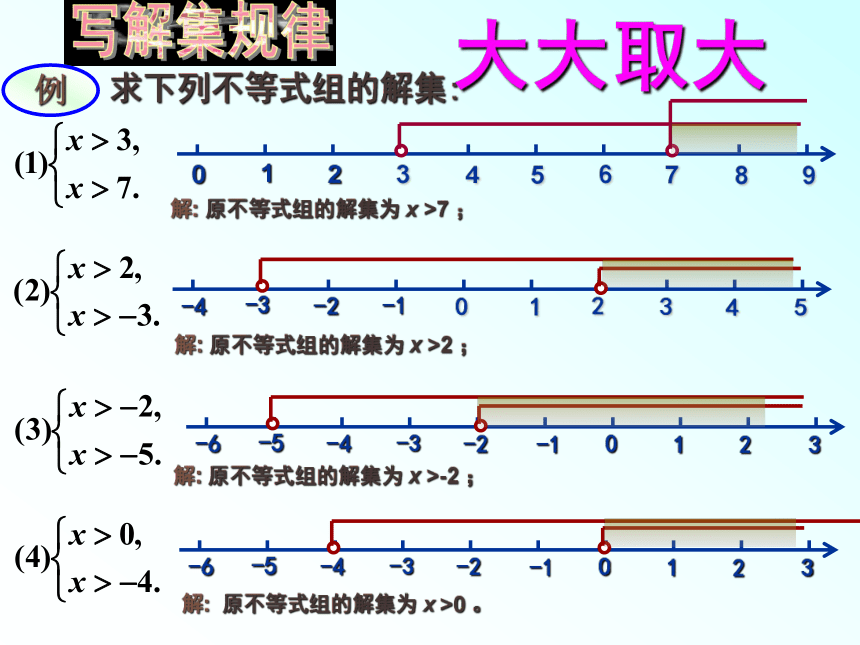
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x >7 ;
解: 原不等式组的解集为 x >2 ;
例
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 x >0 。
-6
1
0
-1
-2
-4
-5
-3
2
3
大大取大
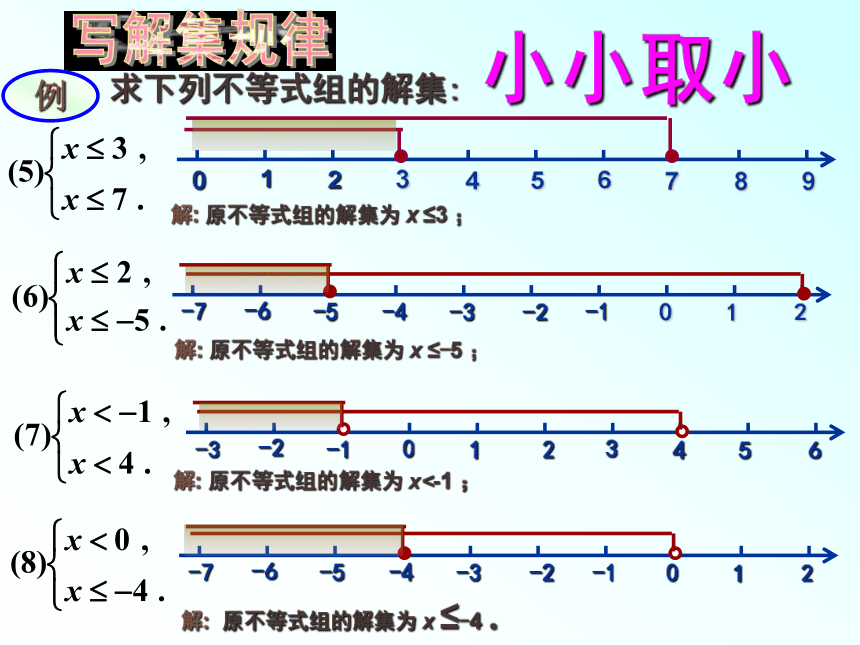
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x ≤3 ;
解: 原不等式组的解集为 x ≤-5 ;
例
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组的解集为 x ≤-4 。
-7
0
-1
-2
-3
-5
-6
-4
1
2
小小取小
例1. 求下列不等式组的解集:
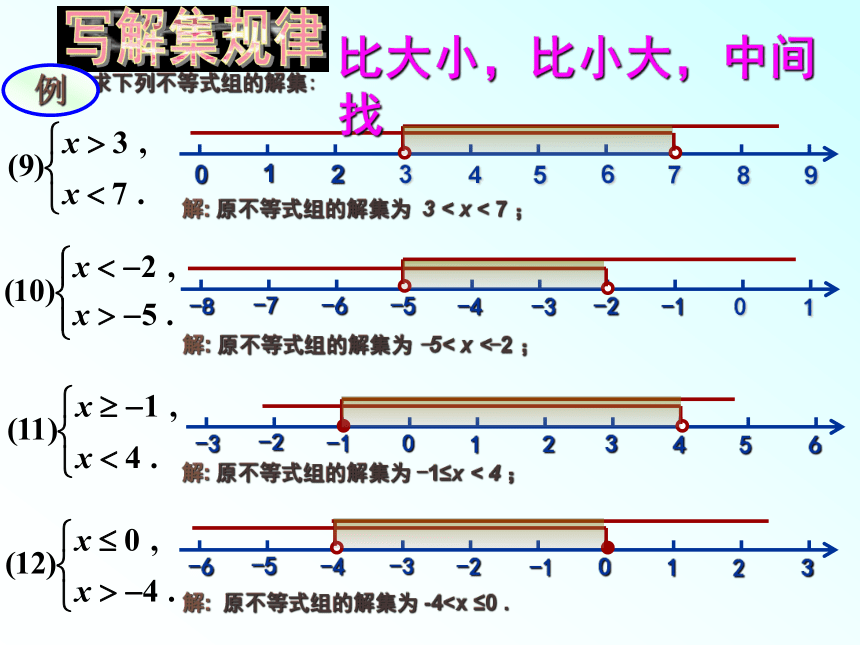
解: 原不等式组的解集为 3 < x < 7 ;
解: 原不等式组的解集为 -5< x <-2 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 -4比大小,比小大,中间找
例1. 求下列不等式组的解集:
解: 原不等式组无解 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组无解 ;
解: 原不等式组无解 ;
解: 原不等式组无解 ;
比大大,比小小, 无解
一元一次不等式组的解集
1.大大取大
2.小小取小
3.比大小,比小大,中间找
4.比大大,比小小,无法找(无解)
第一次尝试:说出下列各不等式组中,每两个不
等式解集的公共部分。
x>2
x>3
{
x<2
x<3
{
x>2
x<3
{
x<2
x>3
{
④
①
②
③
(x>3)
(x<2)
(2(无解)
第二次尝试:解不列不等式组
5x < 0
x+3 < 6
{
①
2x+3 < 5
3x-2 > 4
{
②
2x+3 ≥ -1
4x-2 < 8(x+10)
{
③
x<0
无解
x ≥-2
例 解不等式组
5x -2> 3x+3
①
解:
解不等式① ,得
解不等式② ,得
x > 2.5
x ≤ 4
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
2.5 < x ≤ 4
(观察:数轴上解集的公共部分)
②
x-1
≤ 7 - x
例1、解不等式组
解:解不等式①,得x>-1
②
①
解不等式② 得
在数轴上表示它们的解集:
-3
-2
-1
0
4
2
1
3
5
解一元一次不等式组的步骤:
求出这个不等式组中各个不等式的解集
借助数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集
0
8
0 2 3
你会了吗 试试看
例1:解下列不等式组
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
⑴
②
①
⑵
②
①
所以不等式组的解集:
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解。
0 1 2 3 4
比一比,看谁又快又好
解下列不等式组
⑴
②
①
⑵
②
①
解:解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
所以不等式的解集:
0 1 2
解:解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
所以不等式的解集:
一.练习
1.已知关于x不等式组
无解,则a的取值范围是___
a>3
2.若不等式组
无解,则m的取值范围是__________。
m ≥1.5
能 力 提 升
3、关于x的不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3 B、a≤-3
C、a>-3 D、a<-3
A
例2(1).若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解: 解不等式①,得,x>m-2
解不等式②,得,x < n + 1
因为不等式组有解,所以
m-2 <x< n + 1
又因为 -1<x<2
所以, m=1 , n=1
-1 2
< x <
m-2
n + 1
m-2= -1 , n + 1 = 2
这里是一个含x的一元一次不等式组,将m,n看作两个已知数,求不等式的解集
解一元一次不等式组
例1 解不等式组
3x-1 > 2x+3
x-1< 2x+1 ②
①
解:
解不等式① ,得
解不等式② ,得
x > 4
x > -2
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
x > 4
(观察:数轴上解集的公共部分)
-
例2 解不等式组
x+3 ≤ 6
①
解:
解不等式① ,得
解不等式② ,得
x ≤ 3
x <1
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
(观察:数轴上解集的公共部分)
②
x <1
x+5
2
<
x+3
3
例3 解不等式组
2x+3 <5
3x-2 >4 ②
①
解:
解不等式① ,得
解不等式② ,得
x < 1
x > 2
在数轴上表示不等式①,②的解集
所以,原不等组无解
(观察:数轴上有无公共部分)
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x >7 ;
解: 原不等式组的解集为 x >2 ;
例
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 x >0 。
-6
1
0
-1
-2
-4
-5
-3
2
3
大大取大
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x ≤3 ;
解: 原不等式组的解集为 x ≤-5 ;
例
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组的解集为 x ≤-4 。
-7
0
-1
-2
-3
-5
-6
-4
1
2
小小取小
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 3 < x < 7 ;
解: 原不等式组的解集为 -5< x <-2 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 -4
例1. 求下列不等式组的解集:
解: 原不等式组无解 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组无解 ;
解: 原不等式组无解 ;
解: 原不等式组无解 ;
比大大,比小小, 无解
一元一次不等式组的解集
1.大大取大
2.小小取小
3.比大小,比小大,中间找
4.比大大,比小小,无法找(无解)
第一次尝试:说出下列各不等式组中,每两个不
等式解集的公共部分。
x>2
x>3
{
x<2
x<3
{
x>2
x<3
{
x<2
x>3
{
④
①
②
③
(x>3)
(x<2)
(2
第二次尝试:解不列不等式组
5x < 0
x+3 < 6
{
①
2x+3 < 5
3x-2 > 4
{
②
2x+3 ≥ -1
4x-2 < 8(x+10)
{
③
x<0
无解
x ≥-2
例 解不等式组
5x -2> 3x+3
①
解:
解不等式① ,得
解不等式② ,得
x > 2.5
x ≤ 4
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
2.5 < x ≤ 4
(观察:数轴上解集的公共部分)
②
x-1
≤ 7 - x
例1、解不等式组
解:解不等式①,得x>-1
②
①
解不等式② 得
在数轴上表示它们的解集:
-3
-2
-1
0
4
2
1
3
5
解一元一次不等式组的步骤:
求出这个不等式组中各个不等式的解集
借助数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集
0
8
0 2 3
你会了吗 试试看
例1:解下列不等式组
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
⑴
②
①
⑵
②
①
所以不等式组的解集:
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解。
0 1 2 3 4
比一比,看谁又快又好
解下列不等式组
⑴
②
①
⑵
②
①
解:解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
所以不等式的解集:
0 1 2
解:解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
所以不等式的解集:
一.练习
1.已知关于x不等式组
无解,则a的取值范围是___
a>3
2.若不等式组
无解,则m的取值范围是__________。
m ≥1.5
能 力 提 升
3、关于x的不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3 B、a≤-3
C、a>-3 D、a<-3
A
例2(1).若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解: 解不等式①,得,x>m-2
解不等式②,得,x < n + 1
因为不等式组有解,所以
m-2 <x< n + 1
又因为 -1<x<2
所以, m=1 , n=1
-1 2
< x <
m-2
n + 1
m-2= -1 , n + 1 = 2
这里是一个含x的一元一次不等式组,将m,n看作两个已知数,求不等式的解集
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
