2.5 实验:用单摆测量重力加速度 同步练习题(word版含答案)
文档属性
| 名称 | 2.5 实验:用单摆测量重力加速度 同步练习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 604.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-03 11:49:10 | ||
图片预览



文档简介
2.5 实验:用单摆测量重力加速度
一、单选题
1.在“用单摆测定重力加速度”的实验中,若测得的g值偏小,可能是因为( )
A.摆球的质量太大
B.测摆长时,将线长加小球直径作为摆长
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次
D.摆球上端未固定牢固,摆动中出现松动,摆线变长
2.有两位同学利用假期分别参观了位于哈尔滨市的“哈尔滨工业大学”和上海市的“复旦大学”,他们各自利用那里实验室中的DIS系统探究了单摆周期T和摆长L的关系。然后通过微信交流实验数据,并用计算机绘制了如图甲所示的图像。另外,去“复旦大学”做研究的同学还利用计算机绘制了他实验用的a、b两个摆球的振动图像,如图乙所示。下列说法正确的是:( )
A.甲图中“复旦大学”的同学所测得的实验结果对应的图线是B
B.甲图中图线的斜率表示对应所在位置的重力加速度的倒数
C.由乙图可知,a、b两摆球振动频率之比为3∶2
D.由乙图可知,时b球振动方向沿y轴正方向
3.在“用单摆测量重力加速度的大小”的实验中,摆球摆动稳定后,当它到达最低点时启动秒表开始计时,并记录此后摆球每次经过最低点的次数n(n=1、2、3...),当数到n=40时刚好停表,此时秒表读数为t。则该单摆的周期为( )
A. B. C. D.
4.在“用单摆测定重力加速度”的实验中,下列所给器材中,哪个组合较好( )
①长1m左右的细线②长30cm左右的细线③直径2cm的塑料球④直径2cm的铁球⑤秒表⑥时钟⑦最小刻度线是厘米的直尺 ⑧最小刻度是毫米的直尺
A.①③⑤⑦ B.①④⑤⑧ C.②④⑥⑦ D.②③⑤⑦
5.在一单摆装置中,摆动物体是个装满水的空心小球,球的正下方有一小孔,当摆开始以小角度摆动时,让水从球中连续流出,直到流完为止,由此摆球的周期将( )
A.逐渐增大 B.逐渐减小
C.先增大后减小 D.先减小后增大
6.某同学利用单摆测量重力加速度,为了使测量误差尽量小,下列说法正确的是( )
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆细线要轻
C.实验时须使摆球可旋转
D.摆长一定的情况下,摆的振幅尽量大
二、多选题
7.如图所示为某同学用单摆利量重力加速度的实验,他测得的重力加速度数值小于当地的重力加速度的实际值,造成这一情况的原因可能是( )
A.开始摆动时振幅较小
B.开始计时时,过早按下秒表
C.在测量完摆长之后悬挂点细线松动
D.测量周期时,误将摆球29次全振动的时间记为30次
8.某同学用单摆测当地的重力加速度。他测出了摆线的长度l和摆动周期T,获得多组T与l的数据,再以T2为纵轴、l为横轴画出函数关系图像,如图所示。已知图线与纵轴的截距为a,图线斜率为k,下列说法正确的是( )
A.若摆球质量分布均匀,摆球半径为
B.若摆球质量分布均匀,摆球直径为
C.测得当地的重力加速度大小为
D.由于摆线长度小于摆长,因此测得的重力加速度值偏小
9.在探究单摆振动周期的实验中,操作上错误或不合理的有( )
A.取单摆的最大偏角大于5°
B.摆球摆动到最高点开始计时
C.防止摆球在水平面内做圆周运动或椭圆运动
D.测出的摆线长就是摆长
E.在平衡位置启动秒表,并开始计数,当摆球第30次经过平衡位置时制动秒表,若读数为t,则
10.小明在做用单摆测定重力加速度的实验中,根据实验数据计算出重力加速度明显小于当地重力加速度,他在实验过程可能出现的错误操作是( )
A.记录秒表读数时,没有注意到记录分钟的指针过了半格
B.记录摆动次数n时,单摆实际摆动了n+1次
C.忘记测量小球直径,用摆线长作为单摆长度进行数据处理
D.测量了小球直径,用摆线长加小球直径作为单摆长度进行数据处理
11.下列关于单摆周期的说法正确的是( )
A.用一个装满砂的漏斗和长细线做成一个单摆,在摆动时砂从漏斗中缓慢漏出,周期不变
B.当升降机向上匀加速运动时(aC.将摆由赤道移到北极,单摆振动周期减小
D.将单摆的摆角由5°增加到10°(不计空气阻力),单摆的周期减小
三、非选择题
12.某同学用单摆测量学校所在地的重力加速度。实验步骤如下:
a.在细线的一端打一个比小球上的孔径稍大些的结,将细线穿过球上的小孔,并把细线上端固定在铁架台的上端;
b.先用游标卡尺测得小球的直径,算出半径,再用刻度尺测量悬挂点与小球下端之间的距离,以两者之差作为摆长L;
c.用停表测量单摆做多次全振动的时间,计算出周期T;
d.改变摆长多次重复实验,测量多组摆长L与对应的周期T的数据,并在坐标纸上做出L-T2的图像;
e.根据图像得出重力加速度的测量值;
f.查询所在地的重力加速度值,与测得的结果进行比较,并进行误差分析。
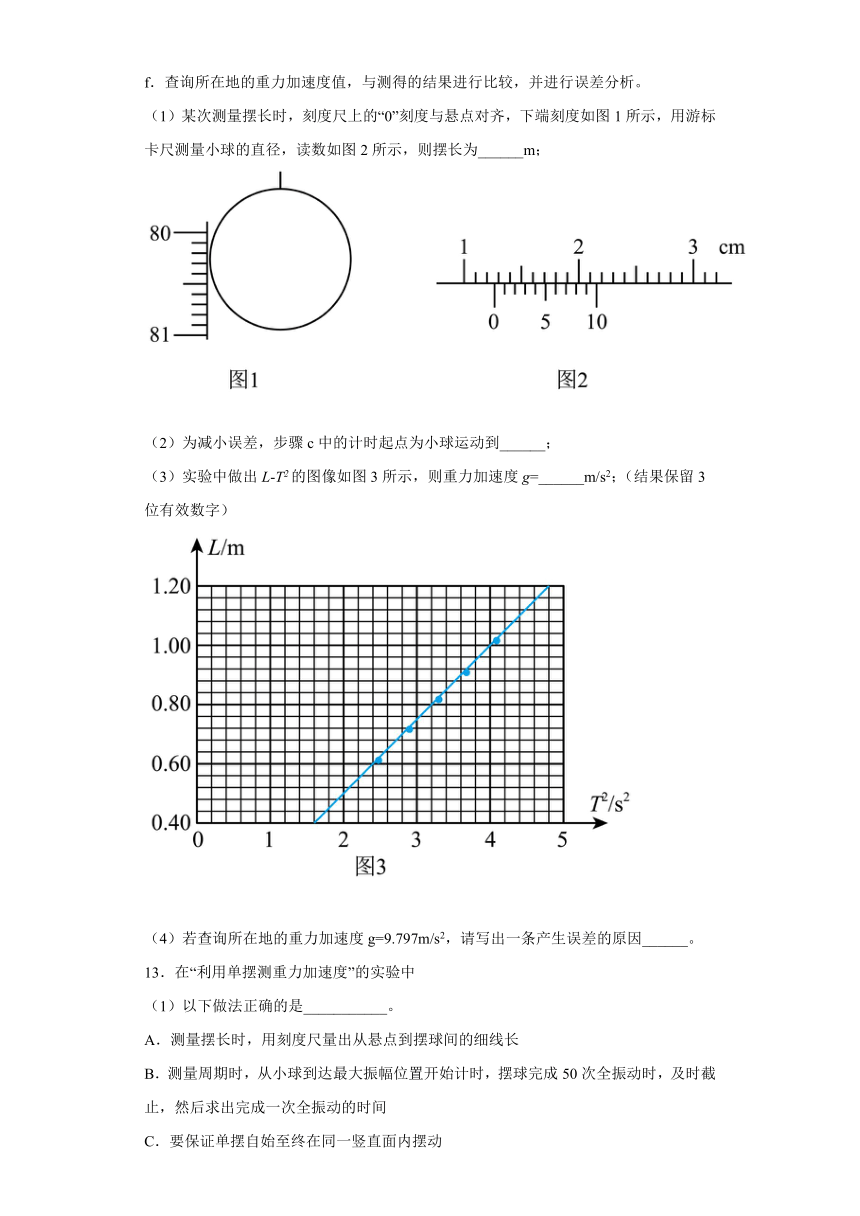
(1)某次测量摆长时,刻度尺上的“0”刻度与悬点对齐,下端刻度如图1所示,用游标卡尺测量小球的直径,读数如图2所示,则摆长为______m;
(2)为减小误差,步骤c中的计时起点为小球运动到______;
(3)实验中做出L-T2的图像如图3所示,则重力加速度g=______m/s2;(结果保留3位有效数字)
(4)若查询所在地的重力加速度g=9.797m/s2,请写出一条产生误差的原因______。
13.在“利用单摆测重力加速度”的实验中
(1)以下做法正确的是___________。
A.测量摆长时,用刻度尺量出从悬点到摆球间的细线长
B.测量周期时,从小球到达最大振幅位置开始计时,摆球完成50次全振动时,及时截止,然后求出完成一次全振动的时间
C.要保证单摆自始至终在同一竖直面内摆动
D.实验时,把单摆从平衡位置拉开30°的摆角
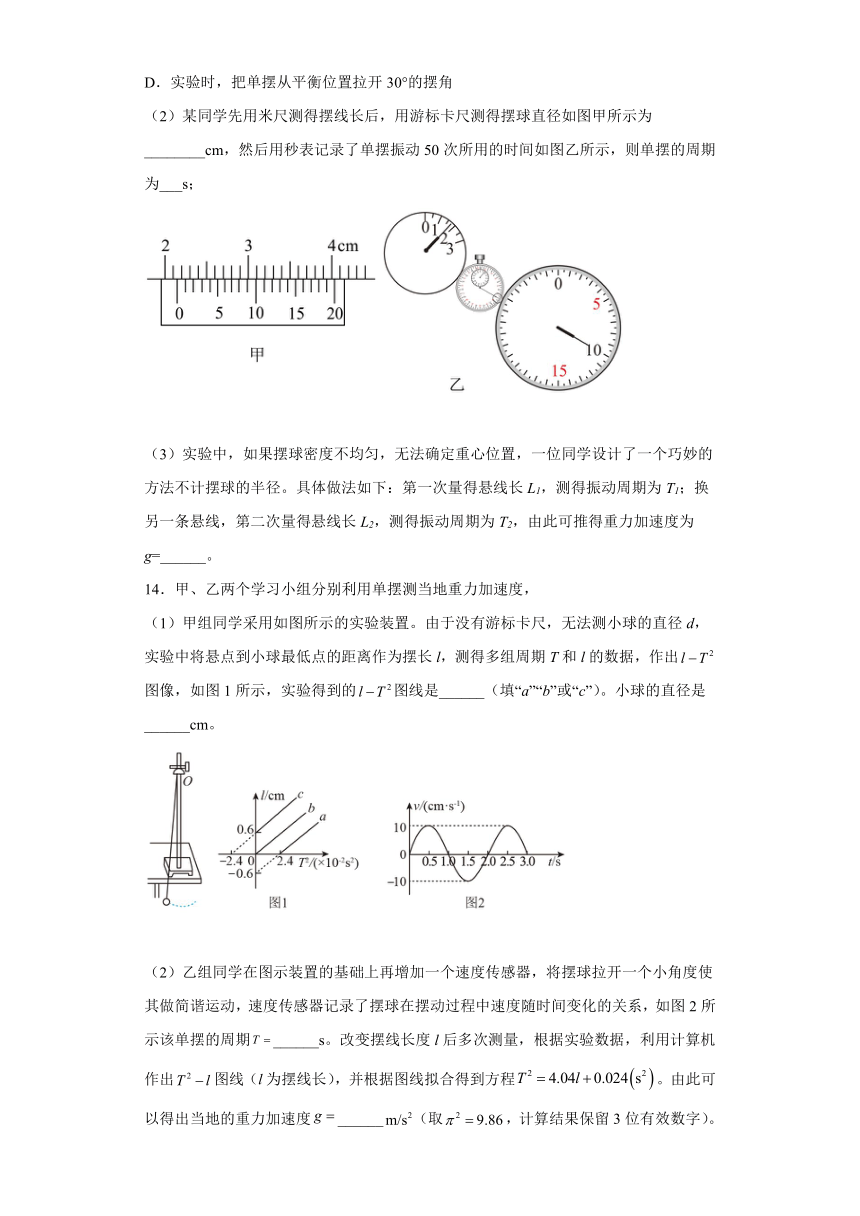
(2)某同学先用米尺测得摆线长后,用游标卡尺测得摆球直径如图甲所示为________cm,然后用秒表记录了单摆振动50次所用的时间如图乙所示,则单摆的周期为___s;
(3)实验中,如果摆球密度不均匀,无法确定重心位置,一位同学设计了一个巧妙的方法不计摆球的半径。具体做法如下:第一次量得悬线长L1,测得振动周期为T1;换另一条悬线,第二次量得悬线长L2,测得振动周期为T2,由此可推得重力加速度为g=______。
14.甲、乙两个学习小组分别利用单摆测当地重力加速度,
(1)甲组同学采用如图所示的实验装置。由于没有游标卡尺,无法测小球的直径d,实验中将悬点到小球最低点的距离作为摆长l,测得多组周期T和l的数据,作出图像,如图1所示,实验得到的图线是______(填“a”“b”或“c”)。小球的直径是______cm。
(2)乙组同学在图示装置的基础上再增加一个速度传感器,将摆球拉开一个小角度使其做简谐运动,速度传感器记录了摆球在摆动过程中速度随时间变化的关系,如图2所示该单摆的周期______s。改变摆线长度l后多次测量,根据实验数据,利用计算机作出图线(l为摆线长),并根据图线拟合得到方程。由此可以得出当地的重力加速度______(取,计算结果保留3位有效数字)。
15.在“用单摆测定重力加速度”实验中:
(1)用游标卡尺测实验所用的匀质小球的直径,如图所示,则小球的直径是__________。
(2)下列做法正确的是___________。(填正确答案的标号)
A.为减少误差应选用轻质小球
B.记录摆球完成一次全振动的时间
C.选用的细线应细、质量小,且不易伸长
D.从摆球到达最高位置时开始计时
(3)实验时改变摆长,测出几组摆线长度为和对应的周期的数据作出图像。如图,利用图中给出的坐标求出重力加速度,其表达式__________,若该同学实验操作步骤完全正确,那么纵轴截距的绝对值是____________。(用表示)
16.“用单摆测定重力加速度”的实验装置如图所示,回答下列小题。
(1)按如图实验装置开始实验,测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g =__________;(用L、n、t表示)
(2)某次实验中,测得摆长为100.00 cm,50次全振动时间为100.0 s。根据数据计算g =________m/s2;(计算结果保留三位有效数字)
(3)用多组实验数据作出T2-L图像,也可以求出重力加速度g。某三位同学作出的T2-L图线如图中的a、b、c所示,其中a和b都是过原点的直线,b和c两直线平行,图线b对应的g值最接近当地重力加速度的值。下列说法正确的是 _____________。
A.图线a对应的测量值g小于图线b对应的测量值g
B.出现图线a的原因可能是误将49次全振动记为50次
C.出现图线c的原因可能是误将悬点到小球下端的距离记为摆长L
D.出现图线c的原因可能是误将悬点到小球上端的细线长度记为摆长L
17.惠更斯在推导出单摆的周期公式后,用一个单摆测出巴黎的重力加速度,小明同学受此启发,在学习完单摆的相关知识后,他也用单摆等器材测量出学校所在地的重力加速度。在测量过程中,他用到了以下的器材:长约的伸缩性小的细绳小钢球、铁架台,刻度尺,游标卡尺、手机秒表等。
(1)按照图1所示装置组装好实验器材,用刻度尺测量摆线的长度l,用游标卡尺测量摆球的直径d。某次测量刻度尺和游标卡尺的示数如图2和图3所示,则在本次测量中,小球的直径___________,单摆摆线的长度___________m。
(2)小明同学用手机秒表测量摆球完成50次全振动的时间如图4所示,这次测量测得单摆振动的周期___________s。(保留两位小数)
(3)小明测量出多组周期T,摆长L数值后,画出图像如图5所示,则此图线的斜率表示的是___________。
A.g B. C. D.
(4)小明比较重力加速度测量值与真实值的大小时,发现测量得到的重力加速度偏大,造成这一现象的原因可能是___________
A.振幅偏小 B.在未悬挂单摆之前先测定摆长
C.将摆线长当成了摆长 D.将摆线长与球的直径之和当成了摆长
18.在“利用单摆测重力加速度”的实验中,某同学想进一步验证单摆的周期和重力加速度的关系,但又不可能去不同的地区做实验。该同学就将单摆与光电门传感器安装在一块摩擦不计、足够大的板上,使板倾斜α角度,让摆球在板的平面内做小角度摆动,如图甲所示。利用该装置可以验证单摆的周期和等效重力加速度的关系。若保持摆长不变,则实验中需要测量的物理量有______。若从实验中得到所测物理量数据的图线如图乙所示,则图象中的纵坐标表示______,横坐标表示______。
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
在“用单摆测定重力加速度”的实验中,根据
得
A.g值与摆球的质量无关,A错误;
B.测摆长时,将线长加小球直径作为摆长,使得偏大,则g值偏大,B错误;
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次,使得g值偏大,C错误;
D.摆球上端未固定牢固,摆动中出现松动,摆线变长,使得测得的比实际值偏小,则g值偏小,D正确。
故选D。
2.C
【解析】
【详解】
AB.根据
得
知图线的斜率
图线B的斜率较小,则图线B对应的重力加速度较大,可知甲图中“哈尔滨工业大学”的同学所测得的实验结果对应的图象是B,故AB错误;
C.周期等于完成一次全振动的时间,由乙图可知,a、b两单摆的周期之比为2:3,振动频率之比为3∶2,故C正确;
D.由乙图可知,t=1s时,b球处于平衡位置向-y方向运动,故D错误。
故选C。
3.C
【解析】
【详解】
由题意可知,单摆完成全振动的次数为
故该单摆的周期为
C正确。
故选C。
4.B
【解析】
【详解】
单摆模型中,小球视为质点,故摆线长点,测量误差越小,故要选择长1m左右的细线①;
摆球密度要大,体积要小,空气阻力的影响才小,故要选择直径2cm的铁球④;
秒表可以控制开始计时和结束计时的时刻,比时钟的效果要好。故选择秒表⑤;
刻度尺的最小分度越小,读数越精确,故要选择最小刻度是毫米的直尺⑧。
故选B。
5.C
【解析】
【详解】
单摆小角度摆动,做简谐运动的周期为,式中L为摆长,其值为悬点到摆动物体重心之间的距离,当小球装满水时,重心在球心,水流完后,重心也在球心,但水刚流出过程中重心要降低,因此,在水的整个流出过程中,重心位置先下降后上升,即摆长Ll先增大后减小,所以摆动周期将先增大后减小。故ABD错误,C正确。
故选C。
6.B
【解析】
【详解】
A.组装单摆须选用密度较大,而直径较小的摆球,选项A错误;
B.组装单摆细线要轻,选项B正确;
C.实验时不能使摆球可旋转,选项C错误;
D.摆长一定的情况下,摆的振幅不能太大,摆角不超过5°,选项D错误。
故选B。
7.BC
【解析】
【详解】
A.单摆的周期
则重力加速度
开始摆动时振幅较小,不影响重力加速度的测量,选项A错误;
B.开始计时时,过早按下秒表,则测量的时间变长,会导致周期变大,重力加速度测量值偏小,选项B正确;
C.在测量完摆长之后悬挂点细线松动,则测量的摆长比实际摆长偏小,导致重力加速度测量值偏小,选项C正确;
D.测量周期时,误将摆球29次全振动的时间记为30次,根据可知测量的周期比实际周期偏小,则重力加速度测量值偏大,选项D错误。
故选BC。
8.AC
【解析】
【详解】
T2与L的图象,应为过原点的直线,但图中没有过原点,且实验中该学生在测量摆长时,只量了悬线的长度l当作摆长,而没有加上摆球的半径r,由单摆周期公式可得
整理可得
由题可知
,
解得
,
则摆球直径为
此实验中误将摆线长当成摆长进行测量和绘制图线,但图线的斜率不变,所测重力加速度不变。
故选AC。
9.ABDE
【解析】
【详解】
A.单摆应保证偏角小于5°,做简谐运动,选项A错误,符合题意;
B.应在通过最低点时开始计时,误差较小,选项B错误,符合题意;
C.防止摆球在水平面内做圆周运动或椭圆运动,选项C正确,不符合题意;
D.摆长应为摆线长加摆球半径,选项D错误,符合题意;
E.如此计数,则周期应为T=,选项E错误,符合题意。
故选ABDE。
10.BC
【解析】
【详解】
根据单摆做简谐振动的周期公式
重力加速度明显偏小,可能是摆长偏小或者是周期偏大的错误操作造成。
A.记录秒表读数时,没有注意到记录分钟的指针过了半格,时间少读了30秒,这样会使周期偏小,测得的重力加速度偏大,选项A错误;
B.记录摆动次数n时,单摆实际摆动了n+1次,这样会使计算出的周期变大,测得的重力加速度偏小,所以B正确;
C.忘记测量小球直径,用摆线长作为单摆长度进行数据处理,计算出的重力加速度变小,C正确;
D.测量了小球直径,用摆线长加小球直径作为单摆长度进行数据处理,计算出的重力加速度变大,选项D错误。
故选BC。
11.BC
【解析】
【详解】
A.根据单摆的周期公式
把l、g理解为等效摆长、等效重力加速度,砂从漏斗中缓慢漏出过程中,重心下降,摆长变长,故周期变长,A错误;
B.匀加速的电梯中,等效重力加速度大于g,故周期变小,B正确;
C.从赤道到北极,重力加速度变大,故周期变小,C正确;
D.单摆摆角在10°以内,可以认为是简谐运动,周期与摆角无关,如果摆角进一步增大,小球的运动不能再看做是简谐运动,周期会变长,D错误。
故选BC。
12. 0.8034 平衡位置 摆长的测量值偏小或周期的测量值偏大
【解析】
【详解】
(1)如图所示
可知刻度尺的读数为80.97cm,游标卡尺的读数为12.6mm,故小球的半径为6.3mm,故摆长为
(2)由于实际摆动过程最高点的位置会发生变化,且在最高点附近速度较小,为减小误差,步骤c中的计时起点为小球运动到平衡位置。
(3)单摆的周期公式为
整理得
由图线的斜率可得
解得
(4)若查询所在地的重力加速度g=9.797m/s2,可知测量值偏小,由周期公式可得
故可能的原因是:摆长的测量值偏小或周期的测量值偏大。
13. C 2.135 2
【解析】
【详解】
(1)A.测量摆长时,用刻度尺量出从悬点到摆球间的细线长L,用游标卡尺测量摆球的直径D,然后用表示摆长。故A错误;
B.测量周期时,从小球到达平衡位置开始计时,摆球完成50次全振动时,及时截止,然后求出完成一次全振动的时间。故B错误;
C.实验过程中要保证单摆自始至终在同一竖直面内摆动。故C正确;
D.实验时,把单摆从平衡位置拉开10°的摆角。故D错误。
故选C。
(2)用游标卡尺测得摆球直径如图甲所示为
秒表读数为
单摆的周期为
(3)根据单摆的周期公式,可得
联立,可得
14. c 1.2 2.0 9.76
【解析】
【详解】
(1)由单摆的周期公式
得
则由数学关系得斜率为
截距
图的截距为正,则图象为c
因截距为
则
(2) 该单摆的周期
由单摆的周期公式
得
结合
图线的斜率
解得
15. 12.5 C
【解析】
【详解】
(1)小球的直径为
(2)A.为减少误差应选用密度较大、体积较小的小球,A错误;
B.应记录摆球完成次全振动的时间,再计算周期,B错误;
C.选用的细线应细、质量小,且不易伸长,C正确;
D.计时起点应从摆球经过最低点时开始计时,D错误。
故选C。
(3)据单摆周期公式可得
整理得
可知,图线的斜率为
故重力加速度的表达式为
当时,,可知纵轴截距的绝对值是小球的半径。
16. 9.86 BD##DB
【解析】
【详解】
(1)根据单摆周期公式
周期测量计算式
解得
(2)将t = 100.00 s,n = 50,L = 1.0000 m, 代入
解得
g = 9.86 m/s2
(3)根据单摆周期公式
整理得
A.由原理可知,T2-L图像的斜率
重力加速度测量值
a图线的斜率小于b图线,可知由a图线求出的g值大于由b图线求出的g值。故A错误;
B.若误将49次全振动记为50次,则每次周期T的测量值都偏小,由图像求斜率
也会偏小,故B正确;
C.若误将悬点到小球下端距离记为摆长L,则T2与L测量值间的函数关系为
其中r为小球半径,图线c应出现横轴正截距,而不是纵轴正截距。故C错误;
D.若误将悬点到小球上端的摆线长度记为摆长L,则T2与L测量值间的函数关系为
其中r为小球半径,图线c出现纵轴正截距。故D正确。
故选BD。
17. 7.50 0.960 1.97 C D
【解析】
【详解】
(1)游标卡尺读数是主尺读数(mm的整数位)加上游标尺读数(mm的小数位),由甲图可读出游标卡尺读数为
刻度尺最小分度为1mm,要估读到下一位,所以读数为96.0cm=0.960m
(2)单摆周期
由图4可知t=98.54s,n=50,带入可得
T=1.97s
(3)由单摆周期公式得
所以图像的斜率表示,故选C。
(4)由单摆周期公式得
摆长测量值偏大、单摆周期测量值偏小都会导致重力加速度偏大,与振幅(最大偏角不超过5°)无关,故ABC错误,D正确。
故选D。
18. 木板倾角α和单摆振动的周期T T2
【解析】
【详解】
此单摆的等效重力加速度为
g′=gsinα
则单摆的周期
则保持摆长不变时,要测量的物理量是:木板倾角α和单摆振动的周期T。
由
可得
则若从实验中得到所测物理量数据的图线如图乙所示,则图像中的纵坐标表示T2,横坐标表示。
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在“用单摆测定重力加速度”的实验中,若测得的g值偏小,可能是因为( )
A.摆球的质量太大
B.测摆长时,将线长加小球直径作为摆长
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次
D.摆球上端未固定牢固,摆动中出现松动,摆线变长
2.有两位同学利用假期分别参观了位于哈尔滨市的“哈尔滨工业大学”和上海市的“复旦大学”,他们各自利用那里实验室中的DIS系统探究了单摆周期T和摆长L的关系。然后通过微信交流实验数据,并用计算机绘制了如图甲所示的图像。另外,去“复旦大学”做研究的同学还利用计算机绘制了他实验用的a、b两个摆球的振动图像,如图乙所示。下列说法正确的是:( )
A.甲图中“复旦大学”的同学所测得的实验结果对应的图线是B
B.甲图中图线的斜率表示对应所在位置的重力加速度的倒数
C.由乙图可知,a、b两摆球振动频率之比为3∶2
D.由乙图可知,时b球振动方向沿y轴正方向
3.在“用单摆测量重力加速度的大小”的实验中,摆球摆动稳定后,当它到达最低点时启动秒表开始计时,并记录此后摆球每次经过最低点的次数n(n=1、2、3...),当数到n=40时刚好停表,此时秒表读数为t。则该单摆的周期为( )
A. B. C. D.
4.在“用单摆测定重力加速度”的实验中,下列所给器材中,哪个组合较好( )
①长1m左右的细线②长30cm左右的细线③直径2cm的塑料球④直径2cm的铁球⑤秒表⑥时钟⑦最小刻度线是厘米的直尺 ⑧最小刻度是毫米的直尺
A.①③⑤⑦ B.①④⑤⑧ C.②④⑥⑦ D.②③⑤⑦
5.在一单摆装置中,摆动物体是个装满水的空心小球,球的正下方有一小孔,当摆开始以小角度摆动时,让水从球中连续流出,直到流完为止,由此摆球的周期将( )
A.逐渐增大 B.逐渐减小
C.先增大后减小 D.先减小后增大
6.某同学利用单摆测量重力加速度,为了使测量误差尽量小,下列说法正确的是( )
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆细线要轻
C.实验时须使摆球可旋转
D.摆长一定的情况下,摆的振幅尽量大
二、多选题
7.如图所示为某同学用单摆利量重力加速度的实验,他测得的重力加速度数值小于当地的重力加速度的实际值,造成这一情况的原因可能是( )
A.开始摆动时振幅较小
B.开始计时时,过早按下秒表
C.在测量完摆长之后悬挂点细线松动
D.测量周期时,误将摆球29次全振动的时间记为30次
8.某同学用单摆测当地的重力加速度。他测出了摆线的长度l和摆动周期T,获得多组T与l的数据,再以T2为纵轴、l为横轴画出函数关系图像,如图所示。已知图线与纵轴的截距为a,图线斜率为k,下列说法正确的是( )
A.若摆球质量分布均匀,摆球半径为
B.若摆球质量分布均匀,摆球直径为
C.测得当地的重力加速度大小为
D.由于摆线长度小于摆长,因此测得的重力加速度值偏小
9.在探究单摆振动周期的实验中,操作上错误或不合理的有( )
A.取单摆的最大偏角大于5°
B.摆球摆动到最高点开始计时
C.防止摆球在水平面内做圆周运动或椭圆运动
D.测出的摆线长就是摆长
E.在平衡位置启动秒表,并开始计数,当摆球第30次经过平衡位置时制动秒表,若读数为t,则
10.小明在做用单摆测定重力加速度的实验中,根据实验数据计算出重力加速度明显小于当地重力加速度,他在实验过程可能出现的错误操作是( )
A.记录秒表读数时,没有注意到记录分钟的指针过了半格
B.记录摆动次数n时,单摆实际摆动了n+1次
C.忘记测量小球直径,用摆线长作为单摆长度进行数据处理
D.测量了小球直径,用摆线长加小球直径作为单摆长度进行数据处理
11.下列关于单摆周期的说法正确的是( )
A.用一个装满砂的漏斗和长细线做成一个单摆,在摆动时砂从漏斗中缓慢漏出,周期不变
B.当升降机向上匀加速运动时(a
D.将单摆的摆角由5°增加到10°(不计空气阻力),单摆的周期减小
三、非选择题
12.某同学用单摆测量学校所在地的重力加速度。实验步骤如下:
a.在细线的一端打一个比小球上的孔径稍大些的结,将细线穿过球上的小孔,并把细线上端固定在铁架台的上端;
b.先用游标卡尺测得小球的直径,算出半径,再用刻度尺测量悬挂点与小球下端之间的距离,以两者之差作为摆长L;
c.用停表测量单摆做多次全振动的时间,计算出周期T;
d.改变摆长多次重复实验,测量多组摆长L与对应的周期T的数据,并在坐标纸上做出L-T2的图像;
e.根据图像得出重力加速度的测量值;
f.查询所在地的重力加速度值,与测得的结果进行比较,并进行误差分析。
(1)某次测量摆长时,刻度尺上的“0”刻度与悬点对齐,下端刻度如图1所示,用游标卡尺测量小球的直径,读数如图2所示,则摆长为______m;
(2)为减小误差,步骤c中的计时起点为小球运动到______;
(3)实验中做出L-T2的图像如图3所示,则重力加速度g=______m/s2;(结果保留3位有效数字)
(4)若查询所在地的重力加速度g=9.797m/s2,请写出一条产生误差的原因______。
13.在“利用单摆测重力加速度”的实验中
(1)以下做法正确的是___________。
A.测量摆长时,用刻度尺量出从悬点到摆球间的细线长
B.测量周期时,从小球到达最大振幅位置开始计时,摆球完成50次全振动时,及时截止,然后求出完成一次全振动的时间
C.要保证单摆自始至终在同一竖直面内摆动
D.实验时,把单摆从平衡位置拉开30°的摆角
(2)某同学先用米尺测得摆线长后,用游标卡尺测得摆球直径如图甲所示为________cm,然后用秒表记录了单摆振动50次所用的时间如图乙所示,则单摆的周期为___s;
(3)实验中,如果摆球密度不均匀,无法确定重心位置,一位同学设计了一个巧妙的方法不计摆球的半径。具体做法如下:第一次量得悬线长L1,测得振动周期为T1;换另一条悬线,第二次量得悬线长L2,测得振动周期为T2,由此可推得重力加速度为g=______。
14.甲、乙两个学习小组分别利用单摆测当地重力加速度,
(1)甲组同学采用如图所示的实验装置。由于没有游标卡尺,无法测小球的直径d,实验中将悬点到小球最低点的距离作为摆长l,测得多组周期T和l的数据,作出图像,如图1所示,实验得到的图线是______(填“a”“b”或“c”)。小球的直径是______cm。
(2)乙组同学在图示装置的基础上再增加一个速度传感器,将摆球拉开一个小角度使其做简谐运动,速度传感器记录了摆球在摆动过程中速度随时间变化的关系,如图2所示该单摆的周期______s。改变摆线长度l后多次测量,根据实验数据,利用计算机作出图线(l为摆线长),并根据图线拟合得到方程。由此可以得出当地的重力加速度______(取,计算结果保留3位有效数字)。
15.在“用单摆测定重力加速度”实验中:
(1)用游标卡尺测实验所用的匀质小球的直径,如图所示,则小球的直径是__________。
(2)下列做法正确的是___________。(填正确答案的标号)
A.为减少误差应选用轻质小球
B.记录摆球完成一次全振动的时间
C.选用的细线应细、质量小,且不易伸长
D.从摆球到达最高位置时开始计时
(3)实验时改变摆长,测出几组摆线长度为和对应的周期的数据作出图像。如图,利用图中给出的坐标求出重力加速度,其表达式__________,若该同学实验操作步骤完全正确,那么纵轴截距的绝对值是____________。(用表示)
16.“用单摆测定重力加速度”的实验装置如图所示,回答下列小题。
(1)按如图实验装置开始实验,测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g =__________;(用L、n、t表示)
(2)某次实验中,测得摆长为100.00 cm,50次全振动时间为100.0 s。根据数据计算g =________m/s2;(计算结果保留三位有效数字)
(3)用多组实验数据作出T2-L图像,也可以求出重力加速度g。某三位同学作出的T2-L图线如图中的a、b、c所示,其中a和b都是过原点的直线,b和c两直线平行,图线b对应的g值最接近当地重力加速度的值。下列说法正确的是 _____________。
A.图线a对应的测量值g小于图线b对应的测量值g
B.出现图线a的原因可能是误将49次全振动记为50次
C.出现图线c的原因可能是误将悬点到小球下端的距离记为摆长L
D.出现图线c的原因可能是误将悬点到小球上端的细线长度记为摆长L
17.惠更斯在推导出单摆的周期公式后,用一个单摆测出巴黎的重力加速度,小明同学受此启发,在学习完单摆的相关知识后,他也用单摆等器材测量出学校所在地的重力加速度。在测量过程中,他用到了以下的器材:长约的伸缩性小的细绳小钢球、铁架台,刻度尺,游标卡尺、手机秒表等。
(1)按照图1所示装置组装好实验器材,用刻度尺测量摆线的长度l,用游标卡尺测量摆球的直径d。某次测量刻度尺和游标卡尺的示数如图2和图3所示,则在本次测量中,小球的直径___________,单摆摆线的长度___________m。
(2)小明同学用手机秒表测量摆球完成50次全振动的时间如图4所示,这次测量测得单摆振动的周期___________s。(保留两位小数)
(3)小明测量出多组周期T,摆长L数值后,画出图像如图5所示,则此图线的斜率表示的是___________。
A.g B. C. D.
(4)小明比较重力加速度测量值与真实值的大小时,发现测量得到的重力加速度偏大,造成这一现象的原因可能是___________
A.振幅偏小 B.在未悬挂单摆之前先测定摆长
C.将摆线长当成了摆长 D.将摆线长与球的直径之和当成了摆长
18.在“利用单摆测重力加速度”的实验中,某同学想进一步验证单摆的周期和重力加速度的关系,但又不可能去不同的地区做实验。该同学就将单摆与光电门传感器安装在一块摩擦不计、足够大的板上,使板倾斜α角度,让摆球在板的平面内做小角度摆动,如图甲所示。利用该装置可以验证单摆的周期和等效重力加速度的关系。若保持摆长不变,则实验中需要测量的物理量有______。若从实验中得到所测物理量数据的图线如图乙所示,则图象中的纵坐标表示______,横坐标表示______。
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
在“用单摆测定重力加速度”的实验中,根据
得
A.g值与摆球的质量无关,A错误;
B.测摆长时,将线长加小球直径作为摆长,使得偏大,则g值偏大,B错误;
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次,使得g值偏大,C错误;
D.摆球上端未固定牢固,摆动中出现松动,摆线变长,使得测得的比实际值偏小,则g值偏小,D正确。
故选D。
2.C
【解析】
【详解】
AB.根据
得
知图线的斜率
图线B的斜率较小,则图线B对应的重力加速度较大,可知甲图中“哈尔滨工业大学”的同学所测得的实验结果对应的图象是B,故AB错误;
C.周期等于完成一次全振动的时间,由乙图可知,a、b两单摆的周期之比为2:3,振动频率之比为3∶2,故C正确;
D.由乙图可知,t=1s时,b球处于平衡位置向-y方向运动,故D错误。
故选C。
3.C
【解析】
【详解】
由题意可知,单摆完成全振动的次数为
故该单摆的周期为
C正确。
故选C。
4.B
【解析】
【详解】
单摆模型中,小球视为质点,故摆线长点,测量误差越小,故要选择长1m左右的细线①;
摆球密度要大,体积要小,空气阻力的影响才小,故要选择直径2cm的铁球④;
秒表可以控制开始计时和结束计时的时刻,比时钟的效果要好。故选择秒表⑤;
刻度尺的最小分度越小,读数越精确,故要选择最小刻度是毫米的直尺⑧。
故选B。
5.C
【解析】
【详解】
单摆小角度摆动,做简谐运动的周期为,式中L为摆长,其值为悬点到摆动物体重心之间的距离,当小球装满水时,重心在球心,水流完后,重心也在球心,但水刚流出过程中重心要降低,因此,在水的整个流出过程中,重心位置先下降后上升,即摆长Ll先增大后减小,所以摆动周期将先增大后减小。故ABD错误,C正确。
故选C。
6.B
【解析】
【详解】
A.组装单摆须选用密度较大,而直径较小的摆球,选项A错误;
B.组装单摆细线要轻,选项B正确;
C.实验时不能使摆球可旋转,选项C错误;
D.摆长一定的情况下,摆的振幅不能太大,摆角不超过5°,选项D错误。
故选B。
7.BC
【解析】
【详解】
A.单摆的周期
则重力加速度
开始摆动时振幅较小,不影响重力加速度的测量,选项A错误;
B.开始计时时,过早按下秒表,则测量的时间变长,会导致周期变大,重力加速度测量值偏小,选项B正确;
C.在测量完摆长之后悬挂点细线松动,则测量的摆长比实际摆长偏小,导致重力加速度测量值偏小,选项C正确;
D.测量周期时,误将摆球29次全振动的时间记为30次,根据可知测量的周期比实际周期偏小,则重力加速度测量值偏大,选项D错误。
故选BC。
8.AC
【解析】
【详解】
T2与L的图象,应为过原点的直线,但图中没有过原点,且实验中该学生在测量摆长时,只量了悬线的长度l当作摆长,而没有加上摆球的半径r,由单摆周期公式可得
整理可得
由题可知
,
解得
,
则摆球直径为
此实验中误将摆线长当成摆长进行测量和绘制图线,但图线的斜率不变,所测重力加速度不变。
故选AC。
9.ABDE
【解析】
【详解】
A.单摆应保证偏角小于5°,做简谐运动,选项A错误,符合题意;
B.应在通过最低点时开始计时,误差较小,选项B错误,符合题意;
C.防止摆球在水平面内做圆周运动或椭圆运动,选项C正确,不符合题意;
D.摆长应为摆线长加摆球半径,选项D错误,符合题意;
E.如此计数,则周期应为T=,选项E错误,符合题意。
故选ABDE。
10.BC
【解析】
【详解】
根据单摆做简谐振动的周期公式
重力加速度明显偏小,可能是摆长偏小或者是周期偏大的错误操作造成。
A.记录秒表读数时,没有注意到记录分钟的指针过了半格,时间少读了30秒,这样会使周期偏小,测得的重力加速度偏大,选项A错误;
B.记录摆动次数n时,单摆实际摆动了n+1次,这样会使计算出的周期变大,测得的重力加速度偏小,所以B正确;
C.忘记测量小球直径,用摆线长作为单摆长度进行数据处理,计算出的重力加速度变小,C正确;
D.测量了小球直径,用摆线长加小球直径作为单摆长度进行数据处理,计算出的重力加速度变大,选项D错误。
故选BC。
11.BC
【解析】
【详解】
A.根据单摆的周期公式
把l、g理解为等效摆长、等效重力加速度,砂从漏斗中缓慢漏出过程中,重心下降,摆长变长,故周期变长,A错误;
B.匀加速的电梯中,等效重力加速度大于g,故周期变小,B正确;
C.从赤道到北极,重力加速度变大,故周期变小,C正确;
D.单摆摆角在10°以内,可以认为是简谐运动,周期与摆角无关,如果摆角进一步增大,小球的运动不能再看做是简谐运动,周期会变长,D错误。
故选BC。
12. 0.8034 平衡位置 摆长的测量值偏小或周期的测量值偏大
【解析】
【详解】
(1)如图所示
可知刻度尺的读数为80.97cm,游标卡尺的读数为12.6mm,故小球的半径为6.3mm,故摆长为
(2)由于实际摆动过程最高点的位置会发生变化,且在最高点附近速度较小,为减小误差,步骤c中的计时起点为小球运动到平衡位置。
(3)单摆的周期公式为
整理得
由图线的斜率可得
解得
(4)若查询所在地的重力加速度g=9.797m/s2,可知测量值偏小,由周期公式可得
故可能的原因是:摆长的测量值偏小或周期的测量值偏大。
13. C 2.135 2
【解析】
【详解】
(1)A.测量摆长时,用刻度尺量出从悬点到摆球间的细线长L,用游标卡尺测量摆球的直径D,然后用表示摆长。故A错误;
B.测量周期时,从小球到达平衡位置开始计时,摆球完成50次全振动时,及时截止,然后求出完成一次全振动的时间。故B错误;
C.实验过程中要保证单摆自始至终在同一竖直面内摆动。故C正确;
D.实验时,把单摆从平衡位置拉开10°的摆角。故D错误。
故选C。
(2)用游标卡尺测得摆球直径如图甲所示为
秒表读数为
单摆的周期为
(3)根据单摆的周期公式,可得
联立,可得
14. c 1.2 2.0 9.76
【解析】
【详解】
(1)由单摆的周期公式
得
则由数学关系得斜率为
截距
图的截距为正,则图象为c
因截距为
则
(2) 该单摆的周期
由单摆的周期公式
得
结合
图线的斜率
解得
15. 12.5 C
【解析】
【详解】
(1)小球的直径为
(2)A.为减少误差应选用密度较大、体积较小的小球,A错误;
B.应记录摆球完成次全振动的时间,再计算周期,B错误;
C.选用的细线应细、质量小,且不易伸长,C正确;
D.计时起点应从摆球经过最低点时开始计时,D错误。
故选C。
(3)据单摆周期公式可得
整理得
可知,图线的斜率为
故重力加速度的表达式为
当时,,可知纵轴截距的绝对值是小球的半径。
16. 9.86 BD##DB
【解析】
【详解】
(1)根据单摆周期公式
周期测量计算式
解得
(2)将t = 100.00 s,n = 50,L = 1.0000 m, 代入
解得
g = 9.86 m/s2
(3)根据单摆周期公式
整理得
A.由原理可知,T2-L图像的斜率
重力加速度测量值
a图线的斜率小于b图线,可知由a图线求出的g值大于由b图线求出的g值。故A错误;
B.若误将49次全振动记为50次,则每次周期T的测量值都偏小,由图像求斜率
也会偏小,故B正确;
C.若误将悬点到小球下端距离记为摆长L,则T2与L测量值间的函数关系为
其中r为小球半径,图线c应出现横轴正截距,而不是纵轴正截距。故C错误;
D.若误将悬点到小球上端的摆线长度记为摆长L,则T2与L测量值间的函数关系为
其中r为小球半径,图线c出现纵轴正截距。故D正确。
故选BD。
17. 7.50 0.960 1.97 C D
【解析】
【详解】
(1)游标卡尺读数是主尺读数(mm的整数位)加上游标尺读数(mm的小数位),由甲图可读出游标卡尺读数为
刻度尺最小分度为1mm,要估读到下一位,所以读数为96.0cm=0.960m
(2)单摆周期
由图4可知t=98.54s,n=50,带入可得
T=1.97s
(3)由单摆周期公式得
所以图像的斜率表示,故选C。
(4)由单摆周期公式得
摆长测量值偏大、单摆周期测量值偏小都会导致重力加速度偏大,与振幅(最大偏角不超过5°)无关,故ABC错误,D正确。
故选D。
18. 木板倾角α和单摆振动的周期T T2
【解析】
【详解】
此单摆的等效重力加速度为
g′=gsinα
则单摆的周期
则保持摆长不变时,要测量的物理量是:木板倾角α和单摆振动的周期T。
由
可得
则若从实验中得到所测物理量数据的图线如图乙所示,则图像中的纵坐标表示T2,横坐标表示。
答案第1页,共2页
答案第1页,共2页
