青岛版小学四年级数学下册《三角形三边之间的关系及内角和(信息窗2)》教学建议
文档属性
| 名称 | 青岛版小学四年级数学下册《三角形三边之间的关系及内角和(信息窗2)》教学建议 |
|
|
| 格式 | doc | ||
| 文件大小 | 787.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 08:21:13 | ||
图片预览


文档简介
《三角形三边之间的关系及内角和(信息窗2)》教学建议
信息窗2——拼制风筝骨架
本信息窗呈现的是两个小朋友尝试围三角形风筝骨架的情境。在围三角形的过程中,发现问题“怎么围不成三角形呢”,引入对三角形三边关系的研究。
通过该信息窗的学习,了解三角形三边之间的关系,学习三角形的内角和。
教学时,教师可以把这个活动情境引入课堂,组织学生用长短不同的小棒拼制三角形的风筝骨架,通过学生自己提出的问题“任意的3根小棒,能围成一个三角形吗”,引入本节课的学习。
“合作探索”中共有两个红点问题。第一个红点部分是学习三角形任意两边长度的和大于第三边。第二个红点部分是教学三角形内角和是180°。
第一个红点标示的问题是:“任意的3根小棒,能围成一个三角形吗?”教材呈现了两个小朋友用小棒围三角形的情景,引入对三角形三条边之间关系的研究。
教学时,可以引导学生利用标有长度的小棒任意摆三角形,在操作过程中发现有的能围成三角形,有的不能围成。接着,从不能围成的人手,研究它们围不成三角形的原因:两条较短边的长度和比第三条边短(或相等),从而推理得出:两条较短边的长度和比第三边长的时候才能围成三角形。然后,通过能围成三角形的例子来验证。最后得出:三角形任意两边长度的和大于第三边。
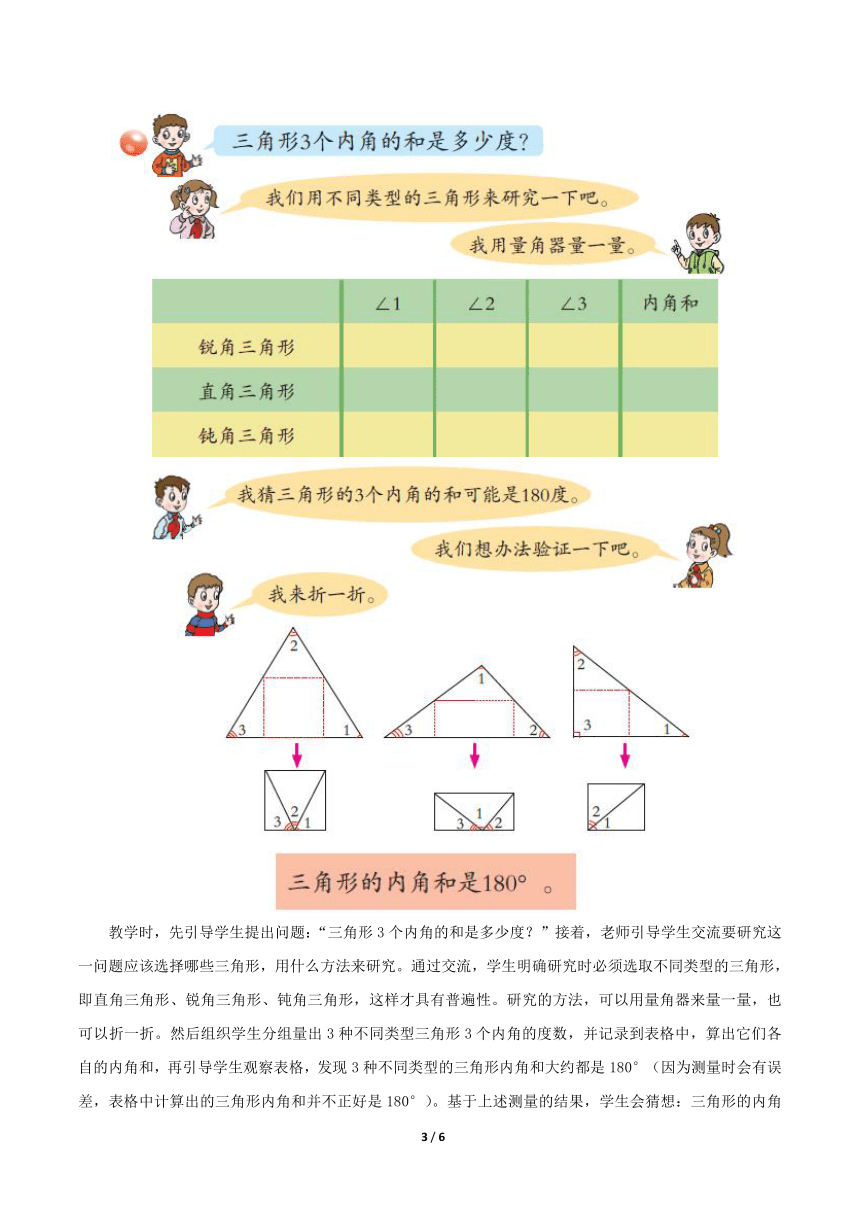
第二个红点标示的问题是:“三角形3个内角的和是多少度呢?”教材的编写意图是让学生用量角器量三角形3个内角的度数,产生三角形的内角和可能是180°的猜想,然后通过折一折去验证猜想,最后得出:三角形3个内角的和是180°。
教学时,先引导学生提出问题:“三角形3个内角的和是多少度?”接着,老师引导学生交流要研究这一问题应该选择哪些三角形,用什么方法来研究。通过交流,学生明确研究时必须选取不同类型的三角形,即直角三角形、锐角三角形、钝角三角形,这样才具有普遍性。研究的方法,可以用量角器来量一量,也可以折一折。然后组织学生分组量出3种不同类型三角形3个内角的度数,并记录到表格中,算出它们各自的内角和,再引导学生观察表格,发现3种不同类型的三角形内角和大约都是180°(因为测量时会有误差,表格中计算出的三角形内角和并不正好是180°)。基于上述测量的结果,学生会猜想:三角形的内角和可能是180°。随后,教师引导学生想出对折的办法验证上述猜想。学生通过折一折,发现不同类型的三角形3个内角都可以拼成一个平角,也就是180°。为了清晰起见,教师可以把对折的过程及结果用多媒体课件动态演示。最后,师生共同归纳得出:三角形的内角和是180°。以上教学过程,由猜想——验证——总结归纳,学生很好地经历了探索“三角形的内角和是180°”的建模过程,积累了丰富的数学活动经验。
“自主练习”第1题是应用三角形三边关系来判断能不能围成三角形的练习题。练习时,可以让学生口答交流,说一说想法再判断。
第2题是运用“三角形的内角和是180°”进行计算的练习题。练习时,可以让学生列出算式,独立完成。
第3、4题是运用“三角形内角和是180°”和“等腰三角形两底角相等”的知识解决问题的练习题。这是一道综合题,要引导学生结合学过的知识说清计算的步骤和方法。
第5题是巩固三角形三边关系的开放性练习题。练习时,可以直接通过想象完成,也可以借助操作完成。组织交流时,让学生说明理由。
第6题是灵活运用所学知识作出正确选择的题目。教师可以指导学生独立完成,再引导学生交流想法。
第7题是实践操作题。教师可以引导学生先想一想该怎样剪,说一说这样剪的理由,再动手操作。
第8题是比眼力的练习题。练习时,先让学生自己数一数,在学生交流的过程中,引导学生按一定的规律数。
第9题是一道推理题。教材提供了长方形和正方形的平面图,练习时引导学生根据“三角形的内角和是180°”观察、推算出长方形和正方形的内角和是360°。
1 / 6
信息窗2——拼制风筝骨架
本信息窗呈现的是两个小朋友尝试围三角形风筝骨架的情境。在围三角形的过程中,发现问题“怎么围不成三角形呢”,引入对三角形三边关系的研究。
通过该信息窗的学习,了解三角形三边之间的关系,学习三角形的内角和。
教学时,教师可以把这个活动情境引入课堂,组织学生用长短不同的小棒拼制三角形的风筝骨架,通过学生自己提出的问题“任意的3根小棒,能围成一个三角形吗”,引入本节课的学习。
“合作探索”中共有两个红点问题。第一个红点部分是学习三角形任意两边长度的和大于第三边。第二个红点部分是教学三角形内角和是180°。
第一个红点标示的问题是:“任意的3根小棒,能围成一个三角形吗?”教材呈现了两个小朋友用小棒围三角形的情景,引入对三角形三条边之间关系的研究。
教学时,可以引导学生利用标有长度的小棒任意摆三角形,在操作过程中发现有的能围成三角形,有的不能围成。接着,从不能围成的人手,研究它们围不成三角形的原因:两条较短边的长度和比第三条边短(或相等),从而推理得出:两条较短边的长度和比第三边长的时候才能围成三角形。然后,通过能围成三角形的例子来验证。最后得出:三角形任意两边长度的和大于第三边。
第二个红点标示的问题是:“三角形3个内角的和是多少度呢?”教材的编写意图是让学生用量角器量三角形3个内角的度数,产生三角形的内角和可能是180°的猜想,然后通过折一折去验证猜想,最后得出:三角形3个内角的和是180°。
教学时,先引导学生提出问题:“三角形3个内角的和是多少度?”接着,老师引导学生交流要研究这一问题应该选择哪些三角形,用什么方法来研究。通过交流,学生明确研究时必须选取不同类型的三角形,即直角三角形、锐角三角形、钝角三角形,这样才具有普遍性。研究的方法,可以用量角器来量一量,也可以折一折。然后组织学生分组量出3种不同类型三角形3个内角的度数,并记录到表格中,算出它们各自的内角和,再引导学生观察表格,发现3种不同类型的三角形内角和大约都是180°(因为测量时会有误差,表格中计算出的三角形内角和并不正好是180°)。基于上述测量的结果,学生会猜想:三角形的内角和可能是180°。随后,教师引导学生想出对折的办法验证上述猜想。学生通过折一折,发现不同类型的三角形3个内角都可以拼成一个平角,也就是180°。为了清晰起见,教师可以把对折的过程及结果用多媒体课件动态演示。最后,师生共同归纳得出:三角形的内角和是180°。以上教学过程,由猜想——验证——总结归纳,学生很好地经历了探索“三角形的内角和是180°”的建模过程,积累了丰富的数学活动经验。
“自主练习”第1题是应用三角形三边关系来判断能不能围成三角形的练习题。练习时,可以让学生口答交流,说一说想法再判断。
第2题是运用“三角形的内角和是180°”进行计算的练习题。练习时,可以让学生列出算式,独立完成。
第3、4题是运用“三角形内角和是180°”和“等腰三角形两底角相等”的知识解决问题的练习题。这是一道综合题,要引导学生结合学过的知识说清计算的步骤和方法。
第5题是巩固三角形三边关系的开放性练习题。练习时,可以直接通过想象完成,也可以借助操作完成。组织交流时,让学生说明理由。
第6题是灵活运用所学知识作出正确选择的题目。教师可以指导学生独立完成,再引导学生交流想法。
第7题是实践操作题。教师可以引导学生先想一想该怎样剪,说一说这样剪的理由,再动手操作。
第8题是比眼力的练习题。练习时,先让学生自己数一数,在学生交流的过程中,引导学生按一定的规律数。
第9题是一道推理题。教材提供了长方形和正方形的平面图,练习时引导学生根据“三角形的内角和是180°”观察、推算出长方形和正方形的内角和是360°。
1 / 6
