人教版七年级下册数学 5.3.1平行线的性质同步训练 (word版含答案)
文档属性
| 名称 | 人教版七年级下册数学 5.3.1平行线的性质同步训练 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 289.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 07:18:36 | ||
图片预览



文档简介
人教版七年级下册数学平行线的性质同步训练
一.选择题
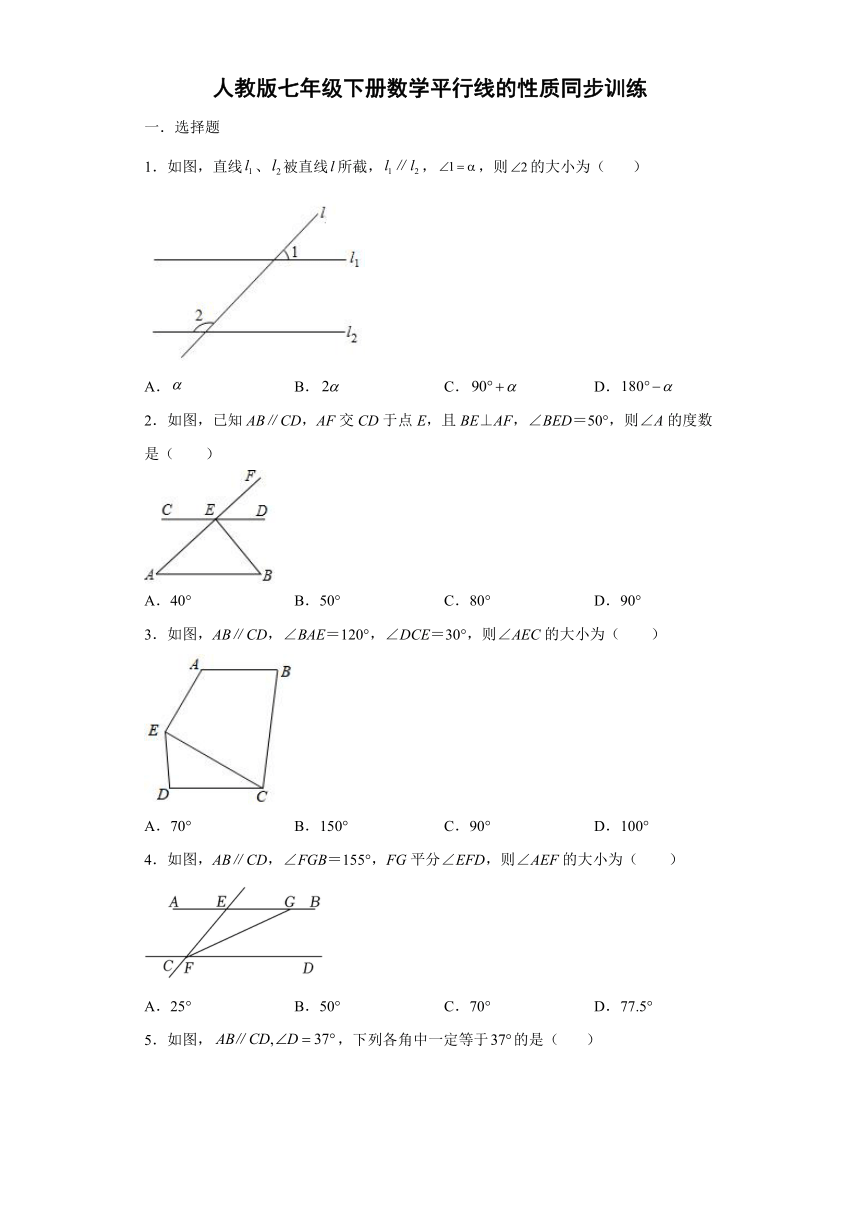
1.如图,直线、被直线所截,,,则的大小为( )
A. B. C. D.
2.如图,已知AB∥CD,AF交CD于点E,且BE⊥AF,∠BED=50°,则∠A的度数是( )
A.40° B.50° C.80° D.90°
3.如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC的大小为( )
A.70° B.150° C.90° D.100°
4.如图,AB∥CD,∠FGB=155°,FG平分∠EFD,则∠AEF的大小为( )
A.25° B.50° C.70° D.77.5°
5.如图,,下列各角中一定等于的是( )
A. B. C. D.
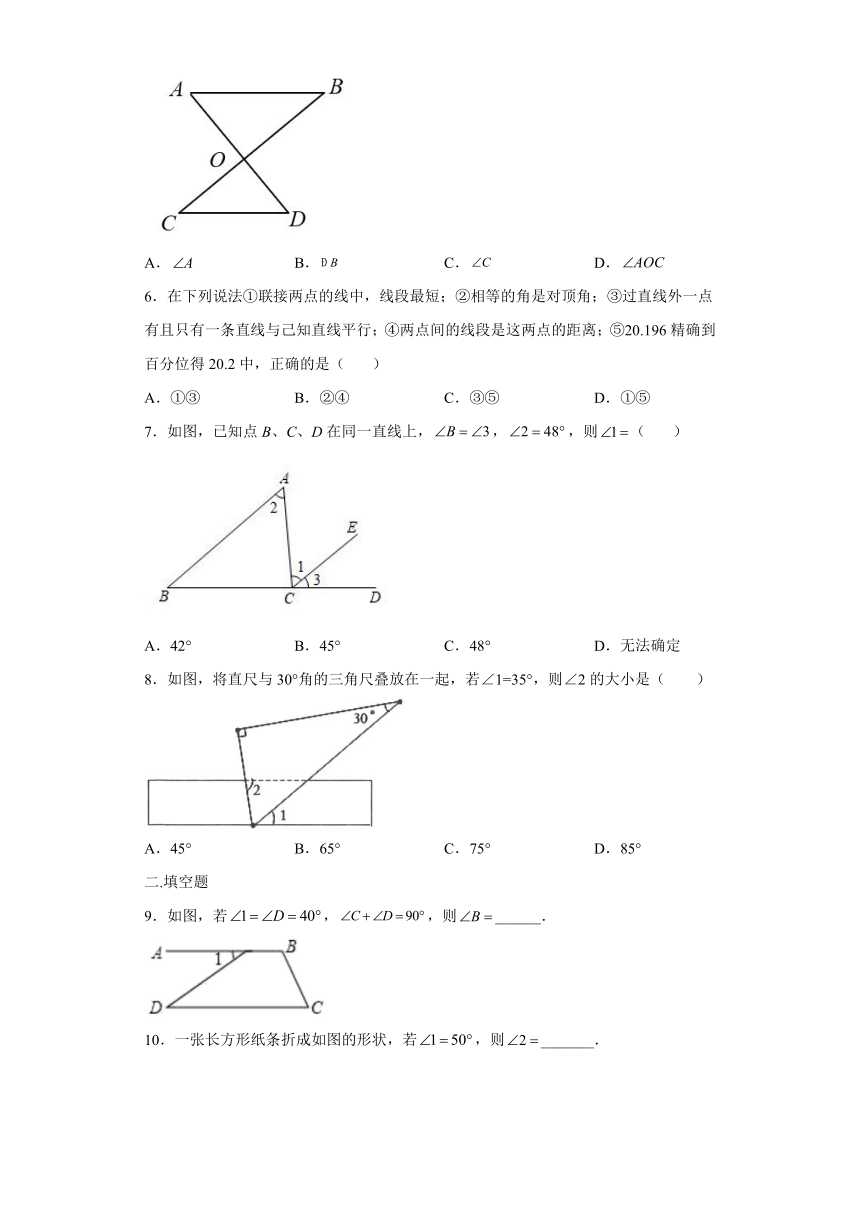
6.在下列说法①联接两点的线中,线段最短;②相等的角是对顶角;③过直线外一点有且只有一条直线与己知直线平行;④两点间的线段是这两点的距离;⑤20.196精确到百分位得20.2中,正确的是( )
A.①③ B.②④ C.③⑤ D.①⑤
7.如图,已知点B、C、D在同一直线上,,,则( )
A.42° B.45° C.48° D.无法确定
8.如图,将直尺与30°角的三角尺叠放在一起,若∠1=35°,则∠2的大小是( )
A.45° B.65° C.75° D.85°
二.填空题
9.如图,若,,则______.
10.一张长方形纸条折成如图的形状,若,则_______.
11.如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAF的度数为_____.
12.如图,直线m∥n.若∠1=40°,∠2=30°,则∠3的大小为_____度.
13.如图,ABCD,EFCD,平分,,则__.
14.一副直角三角板叠放如图所示,现将含30°角的三角板ABC固定不动,把含45°角的三角板ADE绕顶点A顺时针转动,若0°<∠BAD<180°,要使两块三角板至少有一组互相平行,则符合要求的∠BAD的值为________.
15.如图,直线a与直线b平行,将三角板的直角顶点放在直线a上,若∠1=40°,到∠2=__°.
16.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是_______.
三.解答题
17.已知:如图,D,E,F分别是AB,AC,BC上的点,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2.
18.补全下面的解题过程(填理由或数学式).
如图,∠1=50°,∠2=130°,∠C=∠D.求∠A与∠F的数量关系.
解:∵∠1=50°,∠2=130°(已知),
∴∠1+∠2=_______°.
∴_______( ),
∴( ).
∵(已知),
∴_______(等量代换),
∴( ),
∴( ).
19.如图,直线EF分别与直线AB,CD相交于点A,C,AD平分∠BAC,交CD于点D,若∠1=∠2,且∠ADC=54°.
(1)直线AB、CD平行吗?为什么?
(2)求∠1的度数.
20.如图,,求证:.
21.已知:点P在线段BD上,点A在直线MB上,∠E=∠EFC,∠1=∠2
求证:∠DCB+∠MBC=180°
试卷第1页,共3页
参考答案:
1.D
2.A
3.C
4.B
5.A
6.A
7.C
8.D
9.130°
10.
11.35°
12.70
13.
14.45°或90°或120°
15.50
16.
解:如图,过点作,
,
,
,
即
故答案为:
17.
证明:∵DE∥BC,
∴∠ADE=∠ABC.
∵∠ADE=∠EFC,
∴∠ABC=∠EFC.
∴AB∥EF.
∴∠1=∠2.
18.
解:∵∠1=50°,∠2=130°,
∴,
即根据同旁内角互补,两直线平行,
∴,
再根据两直线平行,同位角相等,
∴.
∵,
∴D,
即根据内错角相等,两直线平行,
∴,
又根据两直线平行,内错角相等,
∴.
∴补全的内容为:180;CE;
同旁内角互补,两直线平行;
两直线平行,同位角相等;
D;内错角相等,两直线平行;
两直线平行,内错角相等.
19.
解:,
理由:∵∠1=∠2,∠1=∠DCA,
∴∠2=∠DCA,
∴
(2)
解:∵∠ADC=54°,,
∴∠DAB=∠ADC=54°,
∵AD平分∠BAC,
∴∠BAC=2∠DAB=108°,
∴∠2=180°-∠BAC=72°,
∴∠1=72°.
20.
,
,
,
,
,
,
.
21.
解:∵∠E=∠EFC,
∴AE∥CF,
∴∠1=∠ABC,
∵∠1=∠2,
∴∠ABC=∠2,
∴AB∥CD,
∴∠DCB+∠MBC=180°.
答案第1页,共2页
一.选择题
1.如图,直线、被直线所截,,,则的大小为( )
A. B. C. D.
2.如图,已知AB∥CD,AF交CD于点E,且BE⊥AF,∠BED=50°,则∠A的度数是( )
A.40° B.50° C.80° D.90°
3.如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC的大小为( )
A.70° B.150° C.90° D.100°
4.如图,AB∥CD,∠FGB=155°,FG平分∠EFD,则∠AEF的大小为( )
A.25° B.50° C.70° D.77.5°
5.如图,,下列各角中一定等于的是( )
A. B. C. D.
6.在下列说法①联接两点的线中,线段最短;②相等的角是对顶角;③过直线外一点有且只有一条直线与己知直线平行;④两点间的线段是这两点的距离;⑤20.196精确到百分位得20.2中,正确的是( )
A.①③ B.②④ C.③⑤ D.①⑤
7.如图,已知点B、C、D在同一直线上,,,则( )
A.42° B.45° C.48° D.无法确定
8.如图,将直尺与30°角的三角尺叠放在一起,若∠1=35°,则∠2的大小是( )
A.45° B.65° C.75° D.85°
二.填空题
9.如图,若,,则______.
10.一张长方形纸条折成如图的形状,若,则_______.
11.如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAF的度数为_____.
12.如图,直线m∥n.若∠1=40°,∠2=30°,则∠3的大小为_____度.
13.如图,ABCD,EFCD,平分,,则__.
14.一副直角三角板叠放如图所示,现将含30°角的三角板ABC固定不动,把含45°角的三角板ADE绕顶点A顺时针转动,若0°<∠BAD<180°,要使两块三角板至少有一组互相平行,则符合要求的∠BAD的值为________.
15.如图,直线a与直线b平行,将三角板的直角顶点放在直线a上,若∠1=40°,到∠2=__°.
16.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是_______.
三.解答题
17.已知:如图,D,E,F分别是AB,AC,BC上的点,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2.
18.补全下面的解题过程(填理由或数学式).
如图,∠1=50°,∠2=130°,∠C=∠D.求∠A与∠F的数量关系.
解:∵∠1=50°,∠2=130°(已知),
∴∠1+∠2=_______°.
∴_______( ),
∴( ).
∵(已知),
∴_______(等量代换),
∴( ),
∴( ).
19.如图,直线EF分别与直线AB,CD相交于点A,C,AD平分∠BAC,交CD于点D,若∠1=∠2,且∠ADC=54°.
(1)直线AB、CD平行吗?为什么?
(2)求∠1的度数.
20.如图,,求证:.
21.已知:点P在线段BD上,点A在直线MB上,∠E=∠EFC,∠1=∠2
求证:∠DCB+∠MBC=180°
试卷第1页,共3页
参考答案:
1.D
2.A
3.C
4.B
5.A
6.A
7.C
8.D
9.130°
10.
11.35°
12.70
13.
14.45°或90°或120°
15.50
16.
解:如图,过点作,
,
,
,
即
故答案为:
17.
证明:∵DE∥BC,
∴∠ADE=∠ABC.
∵∠ADE=∠EFC,
∴∠ABC=∠EFC.
∴AB∥EF.
∴∠1=∠2.
18.
解:∵∠1=50°,∠2=130°,
∴,
即根据同旁内角互补,两直线平行,
∴,
再根据两直线平行,同位角相等,
∴.
∵,
∴D,
即根据内错角相等,两直线平行,
∴,
又根据两直线平行,内错角相等,
∴.
∴补全的内容为:180;CE;
同旁内角互补,两直线平行;
两直线平行,同位角相等;
D;内错角相等,两直线平行;
两直线平行,内错角相等.
19.
解:,
理由:∵∠1=∠2,∠1=∠DCA,
∴∠2=∠DCA,
∴
(2)
解:∵∠ADC=54°,,
∴∠DAB=∠ADC=54°,
∵AD平分∠BAC,
∴∠BAC=2∠DAB=108°,
∴∠2=180°-∠BAC=72°,
∴∠1=72°.
20.
,
,
,
,
,
,
.
21.
解:∵∠E=∠EFC,
∴AE∥CF,
∴∠1=∠ABC,
∵∠1=∠2,
∴∠ABC=∠2,
∴AB∥CD,
∴∠DCB+∠MBC=180°.
答案第1页,共2页
