人教版七年级下册数学 5.2.2平行线及其判定同步训练 (word版含答案)
文档属性
| 名称 | 人教版七年级下册数学 5.2.2平行线及其判定同步训练 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 167.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 07:22:43 | ||
图片预览


文档简介
人教版七年级下册数学平行线及其判定训练
一.选择题
1.如图,直线a、b被直线c所截.若∠1=55°,则∠2的度数是( )时能判定a∥b.
A.35° B.45° C.125° D.145°
2.在同一平面内,不重合的三条直线的交点有( )个.
A.1或2 B.2或3 C.1或3 D.0或1或2或3
3.如图,直线a、b被c、d所截,且a∥b,则下列结论中正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠2+∠4=180° D.∠1+∠4=180°
4.下列画出的直线a与b不一定平行的是( )
A. B.
C. D.
5.如图,直线a、b被直线c所截,下列选项中不一定能判定a∥b的是( )
A.∠1=∠3 B.∠1=∠4 C.∠2=∠4 D.∠2=∠5
6.如图是我们学过的用直尺和三角尺画平行线的方法示意图,其画图原理是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同旁内角互补
7.如图,能判定直线的条件是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180° D.∠1=∠4
8.如图点E在BC的延长线上,则下列条件中,不能判定ABCD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
二.填空题
9.下列说法:①对顶角相等;②两点之间的线段是两点间的距离;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤一个锐角的补角一定比它的余角大90°,正确的有______.(填序号)
10.在同一平面内有2021条直线a1,a2,a3,…,a2021,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a5的位置关系是_____;a1与a2021的位置关系是_____.
11.如图,如果______,那么.
12.同一平面内,两条直线相交有__________个交点,两条直线相交的特殊位置关系是__________.
13.如图,图中∠2的同位角是______,内错角是_______,同旁内角是_______.
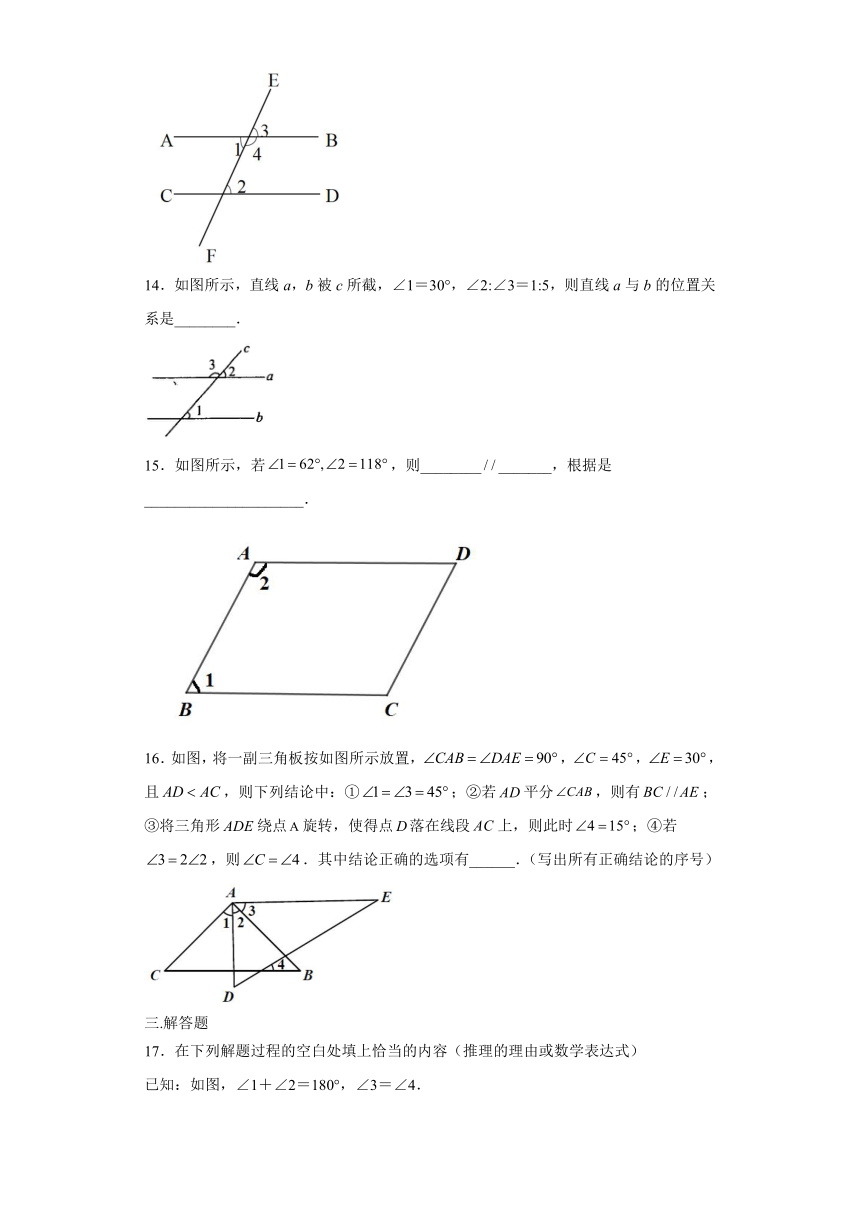
14.如图所示,直线a,b被c所截,∠1=30°,∠2:∠3=1:5,则直线a与b的位置关系是________.
15.如图所示,若,则_______________,根据是_____________________.
16.如图,将一副三角板按如图所示放置,,,,且,则下列结论中:①;②若平分,则有;③将三角形绕点旋转,使得点落在线段上,则此时;④若,则.其中结论正确的选项有______.(写出所有正确结论的序号)
三.解答题
17.在下列解题过程的空白处填上恰当的内容(推理的理由或数学表达式)
已知:如图,∠1+∠2=180°,∠3=∠4.
求证:EFGH.
证明:∵∠1+∠2=180°(已知),∠AEG=∠1(______)
∴∠AEG+∠______=180°,
∴ABCD(______),
∴∠AEG=∠EGD(______),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠______(等式的性质),
即∠FEG=∠______,
∴EFGH(______).
18.如图,已知GH、MN分别平分∠AGE、∠DMF,且∠AGH=∠DMN,试说明ABCD的理由.
19.已知:如图,,.求证:.
20.已知如图,∠ABC=∠ADC,BF、DE分别是∠ABC、∠ADC的角平分线,∠1=∠2,那么CD与AB平行吗 写出推理过程.
试卷第1页,共3页
参考答案:
1.C
2.D
3.B
4.A
5.B
6.A
7.D
8.C
9.①⑤
10. 平行 平行
11..
12. 1 垂直
14.平行
15. AD BC 同旁内角互补,两直线平行
16.②③④
17
证明:∵∠1+∠2=180°(已知),∠AEG=∠1(对顶角相等)
∴∠AEG+∠2=180°,
∴ABCD(同旁内角互补,两直线平行),
∴∠AEG=∠EGD(两直线平行,内错角相等),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠EGD(等式性质),
即∠FEG=∠EGH
∴EFGH(内错角相等,两直线平行)
故答案为:对顶角相等;2;同旁内角互补,两直线平行;两直线平行,内错角相等;EGD;EGH;内错角相等,两直线平行
18.
∵GH平分∠AGE,
∴∠AGE=2∠AGH
同理∠DMF=2∠DMN
∵∠AGH=∠DMN
∴∠AGE=∠DMF
又∵∠AGE=∠FGB
∴∠DMF=∠FGB
∴ABCD (同位角相等,两直线平行).
19.
证明:,,
,
.
20.
解:CD∥AB.理由如下:
∵BF、DE分别是∠ABC、∠ADC的角平分线,
∴∠3=∠ADC,∠2=∠ABC.
∵∠ABC=∠ADC,
∴∠3=∠2.
又∵∠1=∠2,
∴∠3=∠1.
∴CD∥AB(内错角相等,两直线平行).
答案第1页,共2页
一.选择题
1.如图,直线a、b被直线c所截.若∠1=55°,则∠2的度数是( )时能判定a∥b.
A.35° B.45° C.125° D.145°
2.在同一平面内,不重合的三条直线的交点有( )个.
A.1或2 B.2或3 C.1或3 D.0或1或2或3
3.如图,直线a、b被c、d所截,且a∥b,则下列结论中正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠2+∠4=180° D.∠1+∠4=180°
4.下列画出的直线a与b不一定平行的是( )
A. B.
C. D.
5.如图,直线a、b被直线c所截,下列选项中不一定能判定a∥b的是( )
A.∠1=∠3 B.∠1=∠4 C.∠2=∠4 D.∠2=∠5
6.如图是我们学过的用直尺和三角尺画平行线的方法示意图,其画图原理是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同旁内角互补
7.如图,能判定直线的条件是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180° D.∠1=∠4
8.如图点E在BC的延长线上,则下列条件中,不能判定ABCD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
二.填空题
9.下列说法:①对顶角相等;②两点之间的线段是两点间的距离;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤一个锐角的补角一定比它的余角大90°,正确的有______.(填序号)
10.在同一平面内有2021条直线a1,a2,a3,…,a2021,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a5的位置关系是_____;a1与a2021的位置关系是_____.
11.如图,如果______,那么.
12.同一平面内,两条直线相交有__________个交点,两条直线相交的特殊位置关系是__________.
13.如图,图中∠2的同位角是______,内错角是_______,同旁内角是_______.
14.如图所示,直线a,b被c所截,∠1=30°,∠2:∠3=1:5,则直线a与b的位置关系是________.
15.如图所示,若,则_______________,根据是_____________________.
16.如图,将一副三角板按如图所示放置,,,,且,则下列结论中:①;②若平分,则有;③将三角形绕点旋转,使得点落在线段上,则此时;④若,则.其中结论正确的选项有______.(写出所有正确结论的序号)
三.解答题
17.在下列解题过程的空白处填上恰当的内容(推理的理由或数学表达式)
已知:如图,∠1+∠2=180°,∠3=∠4.
求证:EFGH.
证明:∵∠1+∠2=180°(已知),∠AEG=∠1(______)
∴∠AEG+∠______=180°,
∴ABCD(______),
∴∠AEG=∠EGD(______),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠______(等式的性质),
即∠FEG=∠______,
∴EFGH(______).
18.如图,已知GH、MN分别平分∠AGE、∠DMF,且∠AGH=∠DMN,试说明ABCD的理由.
19.已知:如图,,.求证:.
20.已知如图,∠ABC=∠ADC,BF、DE分别是∠ABC、∠ADC的角平分线,∠1=∠2,那么CD与AB平行吗 写出推理过程.
试卷第1页,共3页
参考答案:
1.C
2.D
3.B
4.A
5.B
6.A
7.D
8.C
9.①⑤
10. 平行 平行
11..
12. 1 垂直
14.平行
15. AD BC 同旁内角互补,两直线平行
16.②③④
17
证明:∵∠1+∠2=180°(已知),∠AEG=∠1(对顶角相等)
∴∠AEG+∠2=180°,
∴ABCD(同旁内角互补,两直线平行),
∴∠AEG=∠EGD(两直线平行,内错角相等),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠EGD(等式性质),
即∠FEG=∠EGH
∴EFGH(内错角相等,两直线平行)
故答案为:对顶角相等;2;同旁内角互补,两直线平行;两直线平行,内错角相等;EGD;EGH;内错角相等,两直线平行
18.
∵GH平分∠AGE,
∴∠AGE=2∠AGH
同理∠DMF=2∠DMN
∵∠AGH=∠DMN
∴∠AGE=∠DMF
又∵∠AGE=∠FGB
∴∠DMF=∠FGB
∴ABCD (同位角相等,两直线平行).
19.
证明:,,
,
.
20.
解:CD∥AB.理由如下:
∵BF、DE分别是∠ABC、∠ADC的角平分线,
∴∠3=∠ADC,∠2=∠ABC.
∵∠ABC=∠ADC,
∴∠3=∠2.
又∵∠1=∠2,
∴∠3=∠1.
∴CD∥AB(内错角相等,两直线平行).
答案第1页,共2页
